複数信号機制御における強化学習と交通工学の
融合的アプローチの考察
- 信号機制御
- 強化学習
- 交通工学
- サブエリア制御
- AI技術
信号制御の品質は交通渋滞や環境負荷といった社会課題に直結しており、その品質は従来、熟練した技術者によって維持・向上されてきた。信号制御では交通工学に基づいてサブエリアと呼ばれる単位で複数の信号を連動させており、この連動要素によって最適化が難しくなっている。そこで近年、AIの発展に伴い、強化学習を用いたサブエリア信号制御手法が数多く提案されている。しかし、これらの多くは、交通工学に基づかず、マルチエージェント強化学習などのAIの技術的アプローチを活用している。そのため、遅れ時間などの評価指標は改善しているとしても、実際の信号制御に適用できるかはまだ十分に検討されているとはいいがたい。そこで、本研究では、まず現状の強化学習による制御と、交通工学の重要なパラメーターであるサイクルやスプリット、オフセットとの関係を調査する。そのうえで、強化学習と交通工学を融合したサブエリア信号制御手法を提案する。具体的には、マルチエージェント強化学習に信号間の連動制約と、現示の秒数制約を追加することを検討し、従来の交通工学を用いない強化学習と比較した。その結果、従来の交通工学を用いない強化学習では、サイクルやスプリットが毎回大幅に変更され、実用的でないことがわかった。そして、強化学習に秒数制約を適用すると、一台当たり遅れ時間が116秒から95秒に減少し、CO2排出量が18%減少したという考察が得られた。一方、連動制約は遅れ時間・CO2排出量の削減に寄与しなかったという考察が得られた。本研究を通して、交通工学と強化学習の融合がもたらす効果的な信号制御手法の可能性が示された。
1. まえがき
現代の世界では交通渋滞が深刻化し、膨大な時間損失や経済的負担、さらには大気汚染など環境問題の原因となっている。例えば、国土交通省の資料1)は、全国で年間約61億時間の渋滞損失が発生している、と指摘する。このような状況を受け、日本政府の第5次社会資本整備重点計画では、持続可能で暮らしやすい地域社会の実現やインフラ分野のデジタル・トランスフォーメーション、脱炭素化が重要な政策目標の一つとして掲げられている。この中で、警察庁は交通の円滑化と安全性の向上に向けた取り組みを推進している2)。
交通の円滑化で重要になる交通管理システムにおける交通信号機制御(以下、信号制御)は、現状、熟練した技術者が現地を調査し、交通工学に基づいて素案を決定、試行を経て導入されている。しかし、近年の少子高齢化による熟練技術者の減少や人件費の高騰によって、機械学習、特に強化学習による信号制御が提案されている。我々も以前、単独信号に対する強化学習を用いた制御方法について調査結果を報告した3)。
ところで、信号機は単独で制御されるものではなく、複数の信号機を統括して制御するのが一般的である。この統括される信号機のひとまとまりをサブエリアと呼び、実務上ではサブエリアごとに制御パラメーターを設定する。既にサブエリア内の複数の信号をまとめて制御する強化学習の論文が提案されている4,5)が、近年の主流の研究はマルチエージェント強化学習(Multi-Agent Reinforcement Learning, MARL)やGraph Convolutional Network(GCN)といった機械学習のテクニックにより最適化を目指している。そのため、遅れ時間などの評価指標は改善していても、実際の信号制御に適用できるかは十分に検討されているとはいいがたい。特に、強化学習による従来手法が現在の交通工学を用いた信号制御の指標であるサイクル、スプリット、オフセットに対してどのような出力をしているか、それが現在の信号制御と比較して実交通流で人間の運転手にとって適切に成り立つものであるかが明らかでない。
そこで、本論文ではまず第2章で現状の強化学習の制御と交通工学の重要なパラメーター、サイクル・オフセット・スプリットを紹介する。そのうえで、第3章で強化学習による信号制御に、従来の交通工学に基づく制約を加える信号制御を提案し、その効果をシミュレーターで実証した結果を第4章で報告する。
2. 従来技術と先行研究
2.1 交通工学による信号制御
一般的な信号機における青、黄、赤の1つの表示のことを現示という。本論文では赤信号に右折矢印が出ている現示も青現示として扱う。一括して統括される信号機群のサブエリア内の複数の信号を制御するうえで、交通工学上最も重要なのがサイクル、オフセット、スプリットの三要素である。(図1)これらについての詳細な計算は交通工学研究会出版の設計手引き、“平面交差の計画と設計”6)を参照されたい。
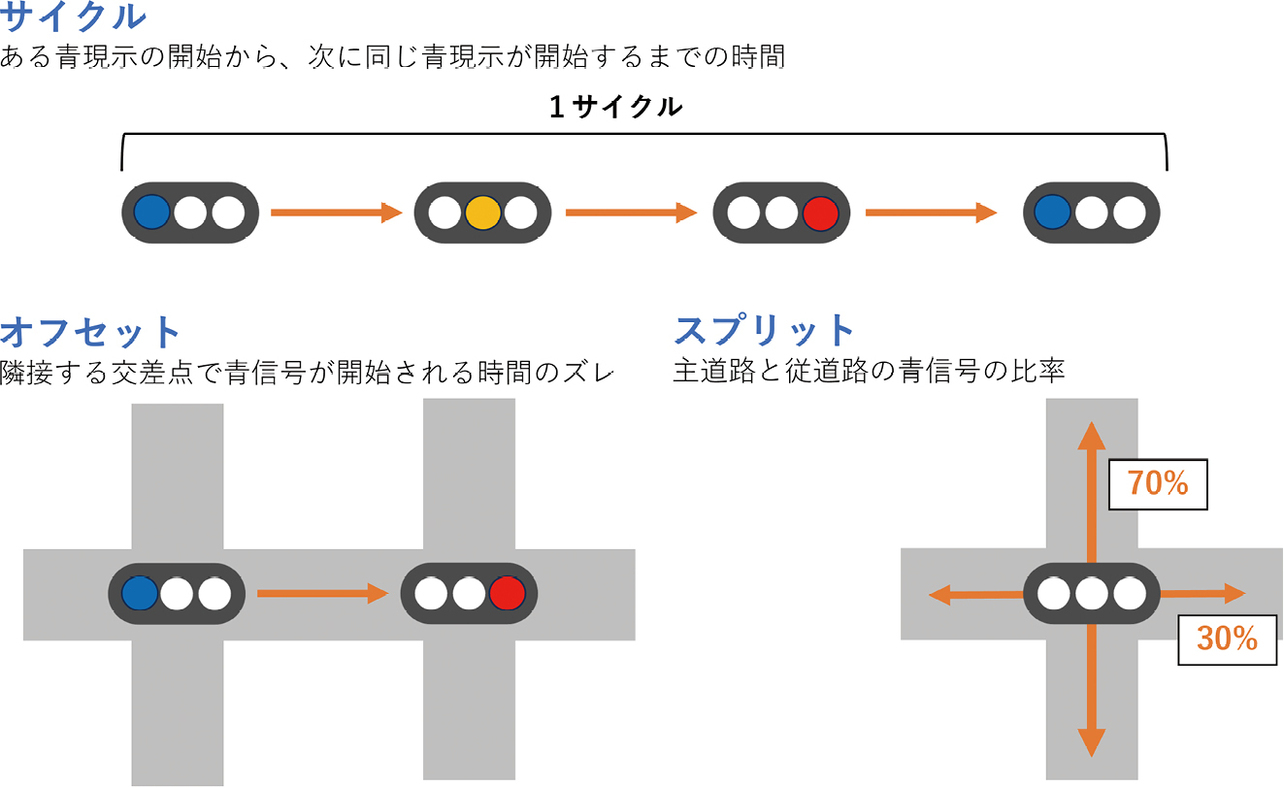
サイクルとは、信号の現示が再び同じ現示に戻るまでの時間のことである。サイクルは、1サイクル中の黄色・赤信号など実質的に車両が通行できない損失時間Lと、交通容量に対する実際の交通量の割合である需要率λを使って計算する。まず、理論上の最小値 を下回るサイクルは、交通容量が交通量を下回るため必ず渋滞する。また、Cminに近いサイクルでは車が少し増えただけでも渋滞が発生するため、多少の余裕を見積もっておく必要がある。その余裕を見積もったサイクルが、車の出現がポアソン分布に従う仮定で最適化されたF. V. Websterによる提案値Cpと、11%の余裕を見積もった交通工学研究会による提案値 であり、下記の式で計算する。
実際の現場では、Cpや の値を参考にして10秒単位でサイクルを設定することが多い。また、サイクルが長すぎると運転者の苛立ちを誘発し、強行突破や信号無視などの危険が生じるため、多くの場合、サイクルは180秒を超えないように設定されている。サイクルごとにオフセットが一定となるよう、サイクル長はサブエリア内で統一することが望ましく、最も長い交差点のサイクルに合わせられることが多い。
オフセットは、隣接する交差点間で信号の開始タイミングにずれを設けるパラメーターである。適切なオフセットが設定されることで、車両は一つの交差点から次の交差点へとスムーズに進行でき、都市部や幹線道路での渋滞緩和につながる。
実際に使われる主なオフセットは3通りである。
- 同時式オフセット:各信号のオフセットを0にし、主道路の青信号を同時に開始する。
- 交互式オフセット:各信号のオフセットをちょうどサイクル長の半分にし、交互に主道路の青信号を開始する。
- 優先式オフセット:主道路を上る(または下る)車が青信号に切り替わって出発したあと、制限速度で走ると、次の信号に差し掛かったときにちょうど主道路の青信号が開始されるように調整される。上りと下りで交通需要に差があるときに採用される。
これらの中から、交通状況に応じて適切なオフセットが設定される。
スプリットは、各進行方向に割り当てる青信号の時間比率を指す。車両の流れが多い方向には長い青信号時間が与えられ、交通量が少ない方向には短い青信号時間が設定されることで、全体の待ち時間の低減や交差点の処理能力向上が図られる。
信号制御の技術者は、サブエリア内で、交通量や交差点形状、交差点間距離を考慮し、適切な信号制御パラメーター(サイクル、スプリット、オフセット)を調整・設定する。
2.2 強化学習
強化学習(Reinforcement Learning, RL)は、エージェントが環境と相互作用しながら、試行錯誤を通じて最適な方策(policy)を学ぶ枠組みである。エージェントは、各時刻において環境の状態を観測し、その情報に基づいて行動を選択する。行動の結果、環境は変化し、エージェントには報酬としてフィードバックが与えられる。報酬は、その行動がどれだけ望ましいものであったかを数値的に示す指標である。エージェントは、累積報酬(リターン)を最大化することを目的として学習を進める。
理論的背景としては、強化学習問題はマルコフ決定過程(Markov Decision Process, MDP)として定式化される。MDPは、状態、行動、報酬、遷移確率の4要素により環境をモデル化する。この枠組みは、エージェントが将来の報酬を最大化するための最適方策の存在や、ベルマン方程式による最適性条件を導出する基盤を提供する。この枠組みにより、強化学習の多くのアルゴリズムは理論的な正当性を持ち、実際の応用においても有効性を示している。
強化学習の枠組みを説明するため、以下の記号を定義する。
- S:エージェントが取りうる状態の全体集合。元はsで表す。
- A:エージェントが取りうる行動の全体集合。元はaで表す。
- P (s' |s,a):状態遷移確率と呼び、現在の状態s∈Sと行動a∈Aによって次の状態s'∈Sが決まる確率のこと。
- r (s,a):即時報酬と呼び、ある状態sで行動aをとったときの報酬のこと。
- γ∈[0,1]:割引率と呼び、将来の報酬をどれだけ重視するかを決めるパラメーター。0に近いほど短期的な報酬を重視し、1に近いほど長期的な報酬を考慮する。
- π:方策と呼び、エージェントが現在の状態に応じてどのような行動を起こすかのルール。特にπ (a|s) と書いたときは、現在の状態がsの時、行動aを選択する確率を示す。また、最適な方策をπ*と書く。
エージェントの目標は、これから得られる累積報酬を最大化することである。ある時刻tにおける累積報酬Gtは次のように定義される。
そして、状態や行動の良さを定量的に表す指標を導入する。ある方策π に従った場合の行動価値関数Qπ (s,a) は、状態s で行動 a を選択した場合の価値関数であり、以下のように定義される。
これは、状態 sで行動 aを選択し、その後方策 πに従って行動したときの期待累積報酬を示す。したがって、最適な行動価値関数Q*(s,a) が得られている場合、エージェントは最も高い行動価値を持つ行動aを選択していくことで、最も高い期待累積報酬が得られる。そのため、最適方策をπ*(s) =argmaxaQ*(s,a) と定めれば最適方策が得られる。
ただし、解析的に行動価値関数を計算できる例は少ない。そこで、遂次的に最適な行動価値関数を求める手法として、Q学習(Q-Learning)が提案されている。Q学習は、行動価値関数が
と再帰的に書き直せることを利用して、
の計算式によって行動価値関数を逐次的に更新することで最適化を狙う。ここで、αは学習率であり、 の項は、次の状態s′ における最大の行動価値を考慮することで、最適な方策を学習することを意味する。ただし、Q学習は状態数と行動数が少ないときは比較的計算しやすいが、状態数と行動数が多くなると途端に計算量が増大し、個別の推定が難しくなってしまう。そこで、ニューラルネットワークを用いて、Q値を推定するのがDeep Q-Network(DQN)7)であり、本論文でもこれを採用している。
2.3 強化学習を用いた信号制御
強化学習を用いた信号制御にはこれまでに様々な方法が提案されている。最初期の2000年代にはWieringやAbdulhaiがQ-learningで信号制御を行った。8,9)2010年代になり、LiがDQNを導入してディープラーニングを用いた信号制御を始めている10)。
さらに、単なる流量と信号の情報だけではなく、上空からの画像を入力とする方法が佐藤11)によって提案されていたり、韓12)は待ち行列推定モデルをDQNに導入したりしている。ただし、佐藤や韓は単一の信号について考察している。これに対して、我々は複数信号を強化学習で決定する方法を、シングルエージェント型、情報交換マルチエージェント型、独立マルチエージェント型の3つに分類して考察する。
シングルエージェント型は、サブエリア全体を単一の強化学習AIエージェントで制御する方法である。全体の情報がエージェントに入力されるため、全体最適は達成しやすい。その一方、信号機の数が増えると状態数と行動数が爆発的に増加する。特に、弊社の担当するサブエリアでは最大で16の信号が存在し、その場合216=65,536通りの行動数となるため、強化学習によって制御するのは現実的ではない。また、サブエリアの信号数や形状によって各信号の状態が異なるため、サブエリアごとに個別の対応が必要となり、スケーラビリティが低い。桑原13)はシングルエージェント型強化学習について報告しており、2信号サブエリアでも非常に多くの学習回数が必要だとしている。
情報交換マルチエージェント型は、各信号に1つのエージェントを配置し、周囲のエージェントと交通量や現在の信号表示など一部の情報を交換し、それを自エージェントの状態として入力して強化学習で制御する方法である。海外での研究報告ではこの型が多く、Wei14)は周辺の交差点の状態を交差点の入力情報として取り込む手法を提案している。西15)やWang16)は、Graph Neural Network(GNN)を用いて情報を交換する手法を提案している。これらの手法はシングルエージェント型と比較して行動数の問題は解決するものの、サブエリアごとに個別の対応が必要なのは変わらず、スケーラビリティが低い。
独立マルチエージェント型は信号1つに対して1つのエージェントを配置し、自エージェントの情報のみで制御を行う方法である。この方法は個別最適が達成できる上に、強化学習エージェントの使いまわしが可能で、スケーラビリティが高いメリットがある。一方、自分の交差点の周辺の情報しか入力として受け取らないため、個別最適にはなっても全体最適とは限らないというデメリットがある。
3. 交通工学と強化学習の組み合わせアルゴリズム
本論文では、第2章で見た3つの分類の中で、独立マルチエージェント型強化学習に交通工学を組み合わせた制御アルゴリズムを提案する。先行研究に多い情報交換マルチエージェント型では、サブエリアごとの個別の対応が必要で、信号制御の検討をする工数が逆に増えてしまうからである。さらに、MARLやGNNなどの複雑なAI技術を用いて全体最適化を試みているが、このような複雑なAI技術は、現場のエンジニアが理解・運用するには手間がかかり、異常発生時の説明可能性も低い。
独立マルチエージェント型を実際の信号制御に実装していくうえで乗り越えるべき課題は2つある。1つ目の課題は、各信号が各々の周囲環境しか考慮せずに個別最適の制御を行った結果、隣との信号の連携が取れていないことである。そのため、青信号で発進した車が次の信号に到着した途端に赤信号になってしまうなど、個別最適にはなっても全体最適には至らない。2つ目の課題は、強化学習の評価関数が最適とは限らず、特にDQNはディープラーニングを用いるために、過学習や誤差の発散、勾配消失・爆発などで、極端な行動を選択することがある。例えば、60秒程度必要な主道路の青信号を3秒で打ち切ってしまったり、逆に3秒で処理可能な従道路の右折が60秒間続いてしまったりすることが発生する。
そこで、我々は交通工学に基づき、独立マルチエージェント型をベースに次の制約を課すことで、上記の2つの課題に対する解決策を提案する。
1つ目の課題に対しては、隣の信号の現示に合わせた制約を設けることで解決を図る。最も混雑する信号の現示は、わずかなズレでも大きな影響を与える。一方で、交通量の少ない信号では、多少のズレによる影響は小さい。そこで、最も混雑する中央信号は自由に制御し、隣接する信号(従属信号)には中央信号の現示状況に依存した一定の制約を課す。具体的には、オフセットが同時オフセットとなるよう、制約を以下のとおりに設けた。
- 従属信号は、中央信号が主道路青の現示の場合、主道路青現示が終了するまで、先の現示に進んではならない。
- 従属信号は、中央信号が主道路青以外の現示の場合、先に次の青現示に進むことは可能だが、それ以降の黄・赤の現示に進んではならない。これ以上先に進むと同時オフセットから交互オフセットとなってしまうためである。
- 中央信号が先に次の現示に進んだ場合、6秒以内に従属信号は次の現示に進む。6秒は黄信号時間3秒+最小青信号時間3秒の和である。これ以上長くなると中央信号が従属信号の2つ先の現示に進んでしまい、同期が取れなくなるためである。
- 交互オフセットを実現する場合は中央信号の主道路と従道路の条件を入れ替える。
これらの制約を今後連動制約と呼ぶ。
2つ目の課題に対しては、短時間すぎて安全上問題があったり、長時間の停止を強いたりするような極端な時間になることを排除するために、最低秒数と最高秒数を現示ごとに設定する。具体的には以下のように設定した。
- 最低秒数:Cmin秒を10秒単位に切り上げたサイクルにおいて、交通量の比率から算出したスプリットで決定した秒数。
- 最高秒数:180秒サイクルにおいて、交通量の比率から算出したスプリットで決定した秒数。
これらの設定により、各信号の現示時間が交通工学で適切な範囲内に収まるようにする。これを時間制約と呼ぶ。
4. 実験方法と結果
4.1 実験条件・評価方法
サブエリアの形状の中では主道路に沿った一直線上に構成されるサブエリアが最も多い。本論文ではこの形状で、幹線道路に沿った一直線上に構成される3つの信号からなるサブエリアを実験対象とした。シミュレーション環境には“Simulation of Urban MObility”(SUMO)17)を利用した。図2のように道路端は左から時計回りにW, N1, N2, N3, E, S3, S2, S1と名付けた。主道路(W-E)は制限速度60 km/hの片側2車線道路で、交差点では約75 mの右折レーンを有する。また、従道路である3本の道路(N1-S1, N2-S2, N3-S3)は、それぞれ制限速度50 km/hの片側1車線道路で、交差点では約75 mの右折レーンを有する。交差点の中心間の距離はどちらも250 mである。
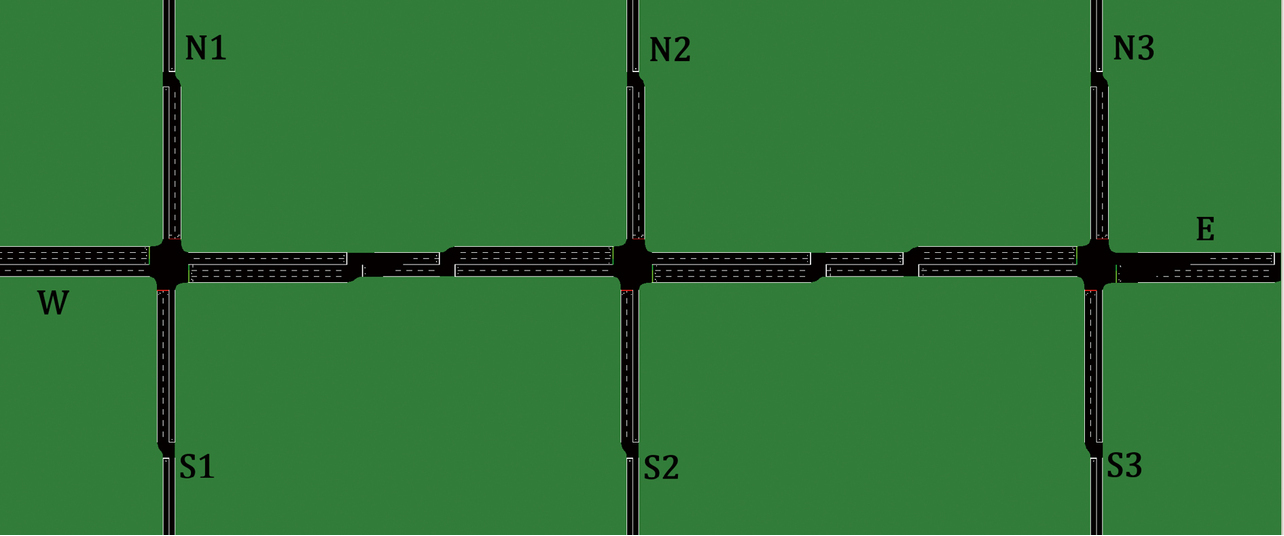
“平面交差の計画と設計”に基づいて計算した従来の定時間制御を比較対象とする。定時間制御は状況に関わらず常に同じ時間で現示が進行する、一番基本的な制御である。定時間制御の各信号の現示の時間は次の表1のとおりである。この値は、表3に定める交通量の需要率λ=0.74から、F. V. Websterの提案値Cp = 88、交通工学研究会の提案値を参考に、サイクルを80秒に設定し、交通量の比率に応じてスプリットを定めたものである。また、今回は交通量の偏りがないため、同時式オフセットに設定した。
| 信号 | サイクル | 主道路 青 |
主道路 右折 |
従道路 青 |
従道路 右折 |
|---|---|---|---|---|---|
| 中央交差点 | 80秒 | 28 | 6 | 25 | 3 |
| 左交差点・右交差点 | 80秒 | 33 | 5 | 21 | 3 |
| From/To [台/時間] |
W | N1 | N2 | N3 | S1 | S2 | S3 | E |
|---|---|---|---|---|---|---|---|---|
| W | \ | 120 | 150 | 120 | 120 | 150 | 120 | 560(P1) 840(P2) 280(P3) |
| N1 | 80 | \ | 0 | 0 | 320 | 0 | 0 | 80 |
| N2 | 100 | 0 | \ | 0 | 0 | 400 | 0 | 100 |
| N3 | 80 | 0 | 0 | \ | 0 | 0 | 320 | 80 |
| S1 | 80 | 320 | 0 | 0 | \ | 0 | 0 | 80 |
| S2 | 100 | 0 | 400 | 0 | 0 | \ | 0 | 100 |
| S3 | 80 | 0 | 0 | 320 | 0 | 0 | \ | 80 |
| E | 560(P1) 840(P2) 280(P3) |
120 | 150 | 120 | 120 | 150 | 120 | \ |
強化学習の時間制約秒数は表2のとおりである。最小はサイクル60秒、最長はサイクル180秒に設定し、交通量の比率に応じてスプリットを定めた時間を設定した。
| 信号 | サイクル | 主道路 青 |
主道路 右折 |
従道路 青 |
従道路 右折 |
|---|---|---|---|---|---|
| 中央交差点 | 最小 (60秒) |
19 | 3 | 18 | 3 |
| 最大 (180秒) |
69 | 18 | 64 | 11 | |
| 左交差点・右交差点 | 最小 (60秒) |
23 | 3 | 15 | 3 |
| 最大 (180秒) |
81 | 17 | 53 | 11 |
強化学習の学習・推論には、SUMO-RL18)のDQNを使用した。DQNに入力される状態sは、現在の信号現示、各車線の車両密度、および各車線の停車車両密度である。行動aは、次の現示に切り替えるか、現在の現示を継続するかの二択である。なお、強化学習による推論に基づく行動が第3章に記載した制約条件を満たさない場合には、制約を満たすもう一方の行動を選択して実行する。例えば、最小秒数を満たしていないのに、強化学習が行動として「次の現示へ切り替え」を選択しても、信号は切り替わらない。逆に、最大秒数に達すれば、強化学習がどのような行動を選択しても信号は切り替わる。報酬rは、行動を起こすことによって生じた遅れ時間の変化量とした。学習は、以下のP1パターン流量を用いて、1,500,000ステップ実施した。
交通流量は、以下の3つの流量パターンを用いて、0秒から10,800秒(3時間)まで検証した。
- P1 表3に定める交通量(中央の信号における需要率λ= 0.74)
- P2 P1において、3,600秒から7,200秒の間だけ、主道路の交通量が増大する(需要率λ= 0.82)
- P3 P1において、3,600秒から7,200秒の間だけ、主道路の交通量が減少する(需要率λ= 0.66)
なお、車両の出現は等間隔ではなく、車両ごとにランダムとする。その時、車両の出現は時間当たりの期待値が設定台数となるポアソン分布に従う。例えば、360台/時間であれば、等間隔に10秒に1度ちょうど車両が出現するのではなく、毎秒ごとに、ポアソン分布 に従って出現する。この場合、90.4%の確率で車が出現せず、9%の確率で車が1台出現し、0.5%の確率で車が2台出現し、0.01%の確率で3台以上同時に出現する。(四捨五入の関係で合計は100%とならない)
評価方法は、1台あたりの出発までの遅延時間である出発待ち時間と、出発後の遅延時間である遅れ時間の合計値とした。SUMOでは出発地点に車両が既に存在しており、新たな車両が出発できない場合、1秒遅らせて再度出発を試みる。このように、出発できずに待機している時間を出発待ち時間と呼ぶ。また、遅れ時間とは、出発地点から終着地点までの実際の所要時間と、常に制限速度で走行した場合の時間との差を指す。これは、信号制御の影響による遅延時間を意味する。
さらに、参考指標として1台あたりのCO2排出量も算出した。CO2排出量はSUMOの標準的計算方法である、The Handbook of Emission Factors for Road Transport Ver 3の、4人乗りのガソリンカーモデルで計算している。これらの結果は、ポアソン分布による確率的な車両出現により偏りが生じる可能性がある。そのため、乱数発生器のシード値を変更して50回の試行を行った。
4.2 実験結果
まず、制約なし強化学習について、乱数シード値が1のシミュレーションの右側交差点のサイクル・スプリットと、中央交差点-右側交差点間のオフセットを図3に示す。(以降、サイクル・オフセット・スプリットの図は乱数シード値が1のシミュレーションの値である。)サイクルが最小30秒から最長130秒、スプリットが30%から90%まで、オフセットがマイナス40秒からプラス40秒までと大きく変動していることがわかる。
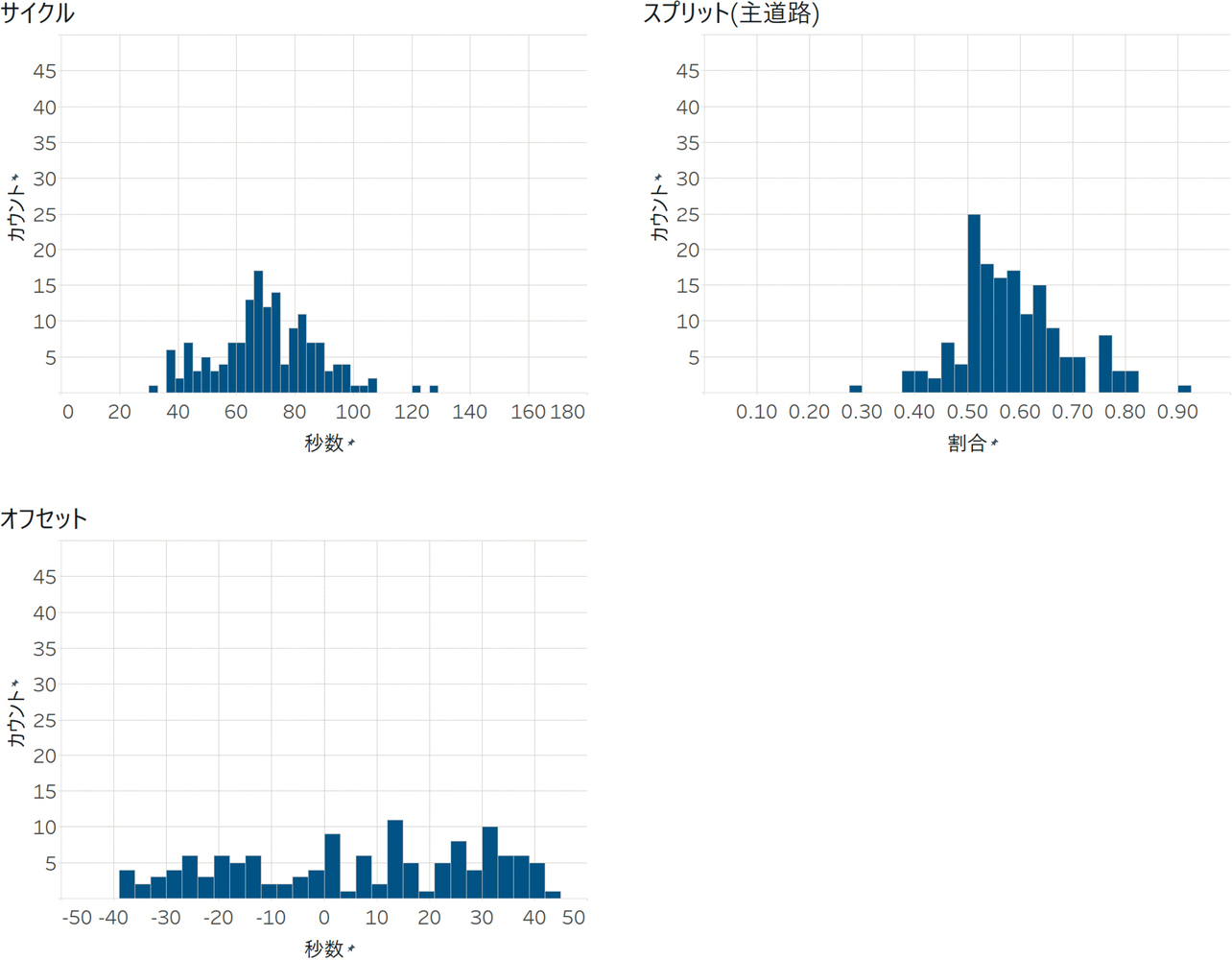
また、表4に遅れ時間・CO2排出量の結果を示す。表では、50回の平均を1段目に示し、標準偏差を2段目に示した。(例:±10.0)P1では、定時間制御と比較して、時間制約のみを付けた強化学習が、遅れ時間とCO2排出量が有意に減少した。時間制約及び連動制約の両方の制約をつけた強化学習では、遅れ時間に有意差はみられなかったが、CO2では有意に減少した。また、P2では、定時間制御と比較して、連動制約のみ以外の強化学習で遅れ時間とCO2排出量が有意に減少した。P3では、時間制約のみ、両方の制約をつけた強化学習が、遅れ時間とCO2排出量が有意に減少した。連動制約のみの強化学習では、すべてのパターンで遅れ時間とCO2排出量が大幅に増加した。なお、有意差検定はウィルコクソン符号付き順位検定を使用した。
| パターン | 評価指標 | 定時間 制御 |
制約なし 強化学習 |
連動制約のみ 強化学習 (提案手法) |
時間制約のみ 強化学習 (提案手法) |
連動制約・ 時間制約 強化学習 (提案手法) |
|---|---|---|---|---|---|---|
| P1 | 遅れ時間+ 出発待ち時間 |
115.9 (±23.2) |
129.3 (±21.2) |
322.88 (±56.0) |
94.8*** (±12.5) |
113.3 (±16.2) |
| CO2排出量 | 530.3 (±47.5) |
511.1* (±15.1) |
679.7 (±51.5) |
434.8*** (±13.3) |
457.6*** (±12.4) |
|
| P2 | 遅れ時間+ 出発待ち時間 |
224.3 (±22.0) |
186.8*** (±21.9) |
518.3 (±70.5) |
141.4*** (±17.2) |
174.5*** (±24.0) |
| CO2排出量 | 667.7 (±17.3) |
575.2*** (±23.1) |
750.0 (±28.5) |
492.6*** (±19.1) |
535.2*** (±25.6) |
|
| P3 | 遅れ時間+ 出発待ち時間 |
97.5 (±12.2) |
99.1 (±11.7) |
182.3 (±35.9) |
77.2*** (±5.5) |
88.9** (±10.1) |
| CO2排出量 | 476.0 (±26.3) |
480.1 (±13.5) |
547.3 (±29.4) |
403.7*** (±9.1) |
425.4*** (±14.2) |
4.3 考察
まず、CO2の排出量と遅れ時間との相関が大きいことがわかる。本実験ではどのような信号制御でも各車両の移動距離自体は変動しない。そのためCO2排出量はアイドリング時間と停止回数に依存する。アイドリング時間と停止回数が減少すれば、当然遅れ時間が減少するため、CO2排出量と遅れ時間の相関は大きい。
次に、制約なしの強化学習では図3で示す通り、サイクルやスプリット、オフセットが大きく変動していることがわかる。特に30秒という極めて短いサイクルでは、今回の交通量を処理するのに十分な長さではない。その場の個別最適を追求するがあまり、長期的な流れや全体最適がつかめていないと考える。また、現実世界において、人間の運転手は交通信号の長さを感覚的にある程度覚えており、その流れに合わせて運転している。しかし、今回の実験結果では、信号のサイクルやスプリットが毎回大きく変動しているため、混乱や効率の低下を招く可能性がある。このようなサイクルやスプリットが大きく変動する制御方式は人間の運転手にとって適切ではなく、現段階では実用的とは言えない。
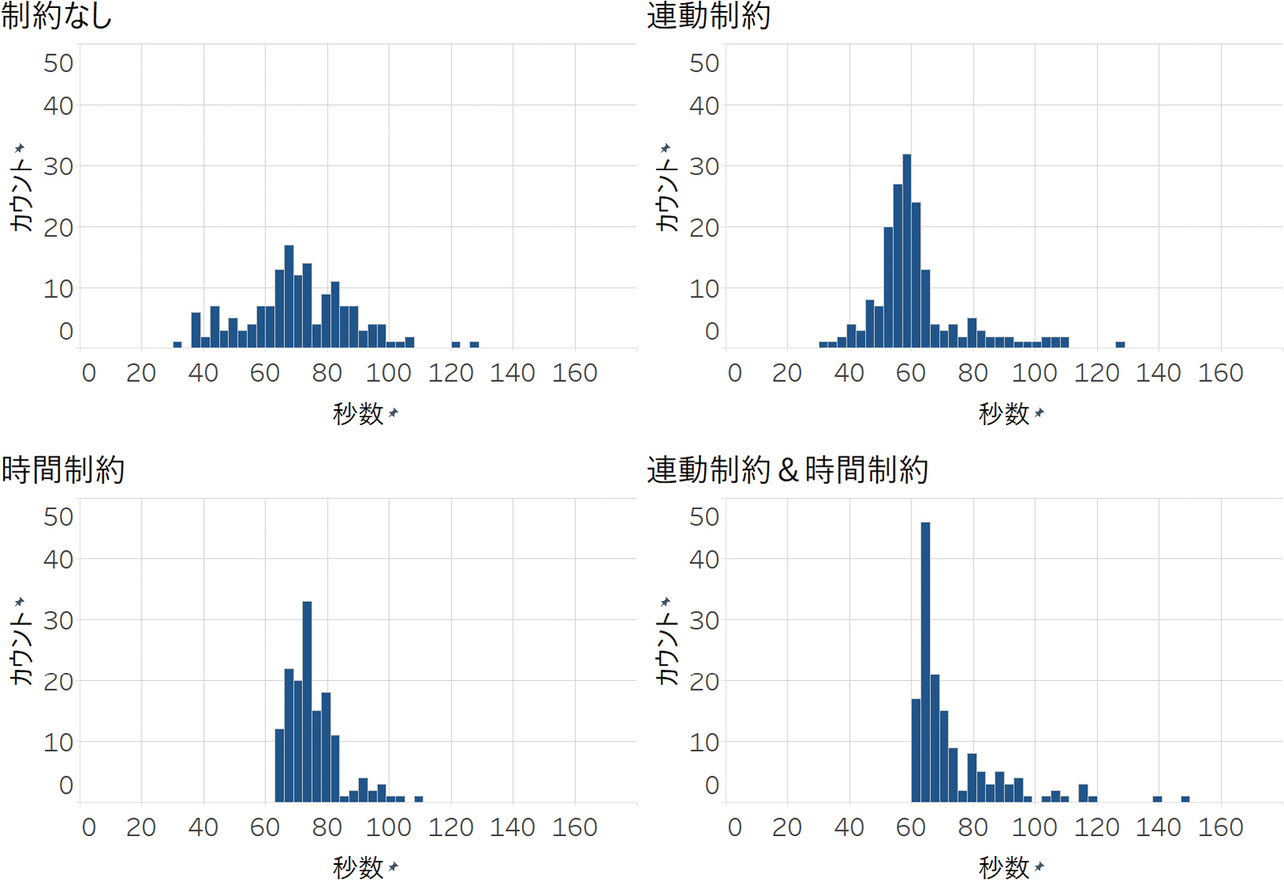
そして、表4を見ると、定時間制御と制約をつけた強化学習の比較結果として、時間制約のみの強化学習が最も遅れ時間を小さくした。これは、秒数制約により、強化学習による早すぎる現示変更を回避できたためである。図4は中央交差点の主道路の青現示の秒数をヒストグラムで表したものである。図4から、制約なしや連動制約のみの場合、最も交通量が多い主道路の青現示が3秒で終了してしまうことがしばしば発生することがわかる。これを原因として、渋滞を引き起こしていることが多い。一方、時間制約を設けることで、主道路の青現示を最低でも21秒確保することで通行量をある程度確保し、強化学習による誤った判断を防ぐことができた。
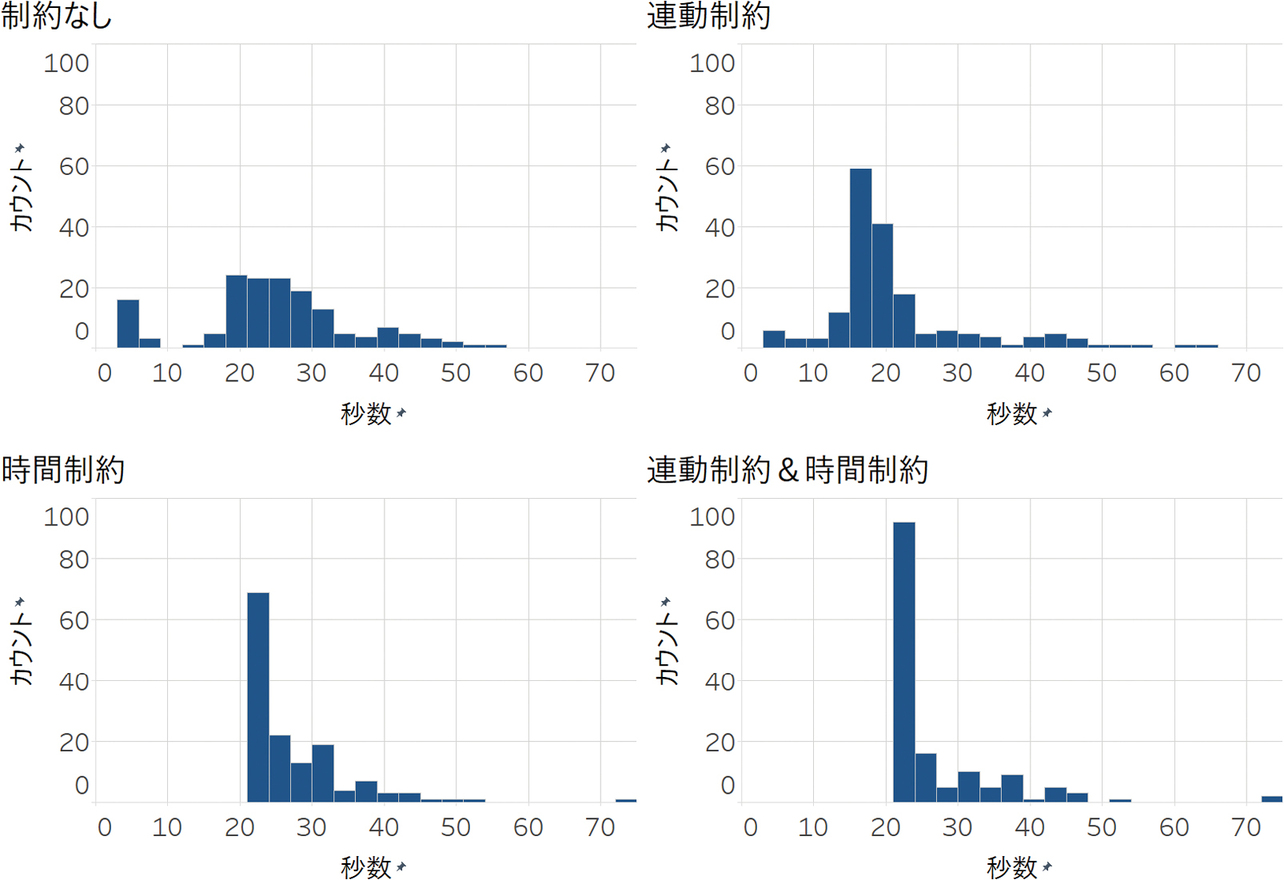
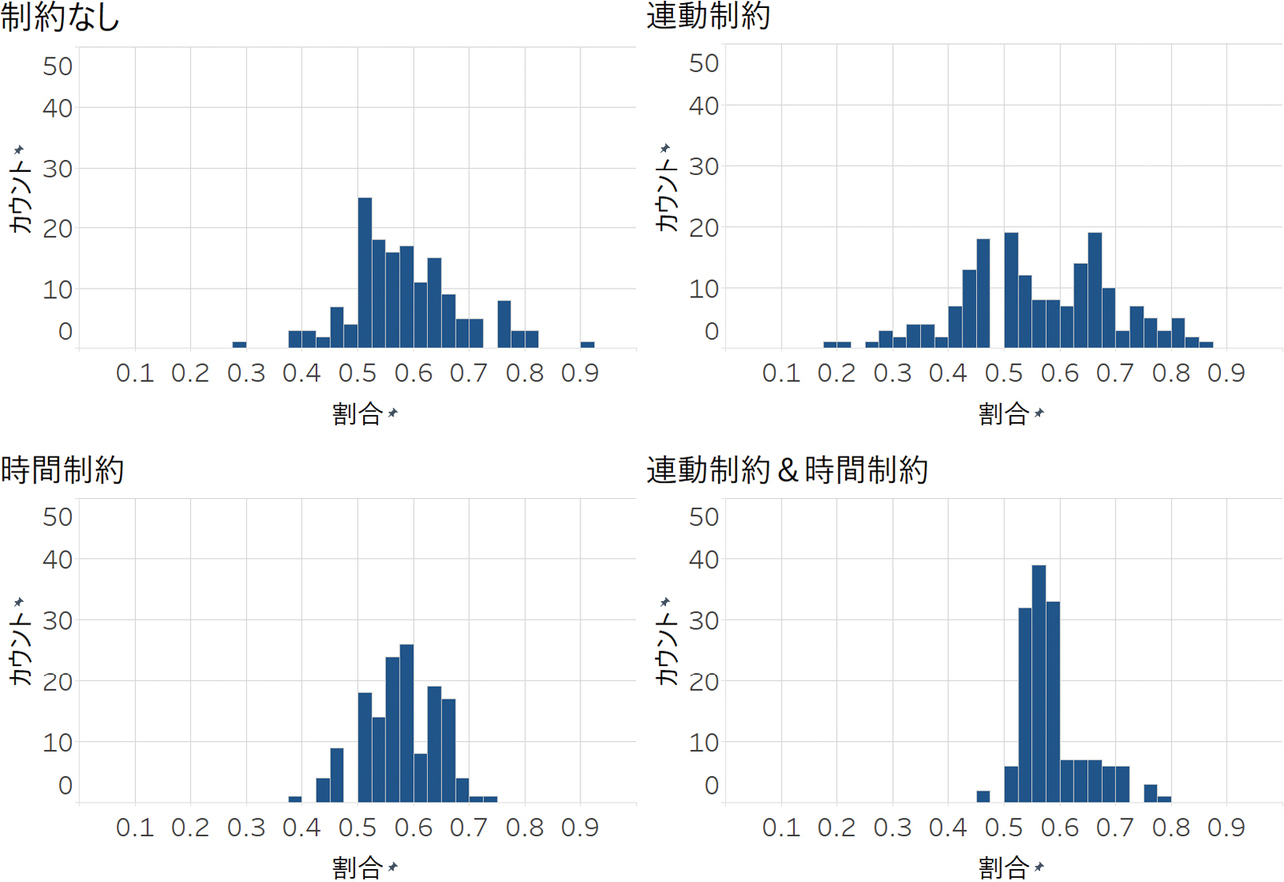
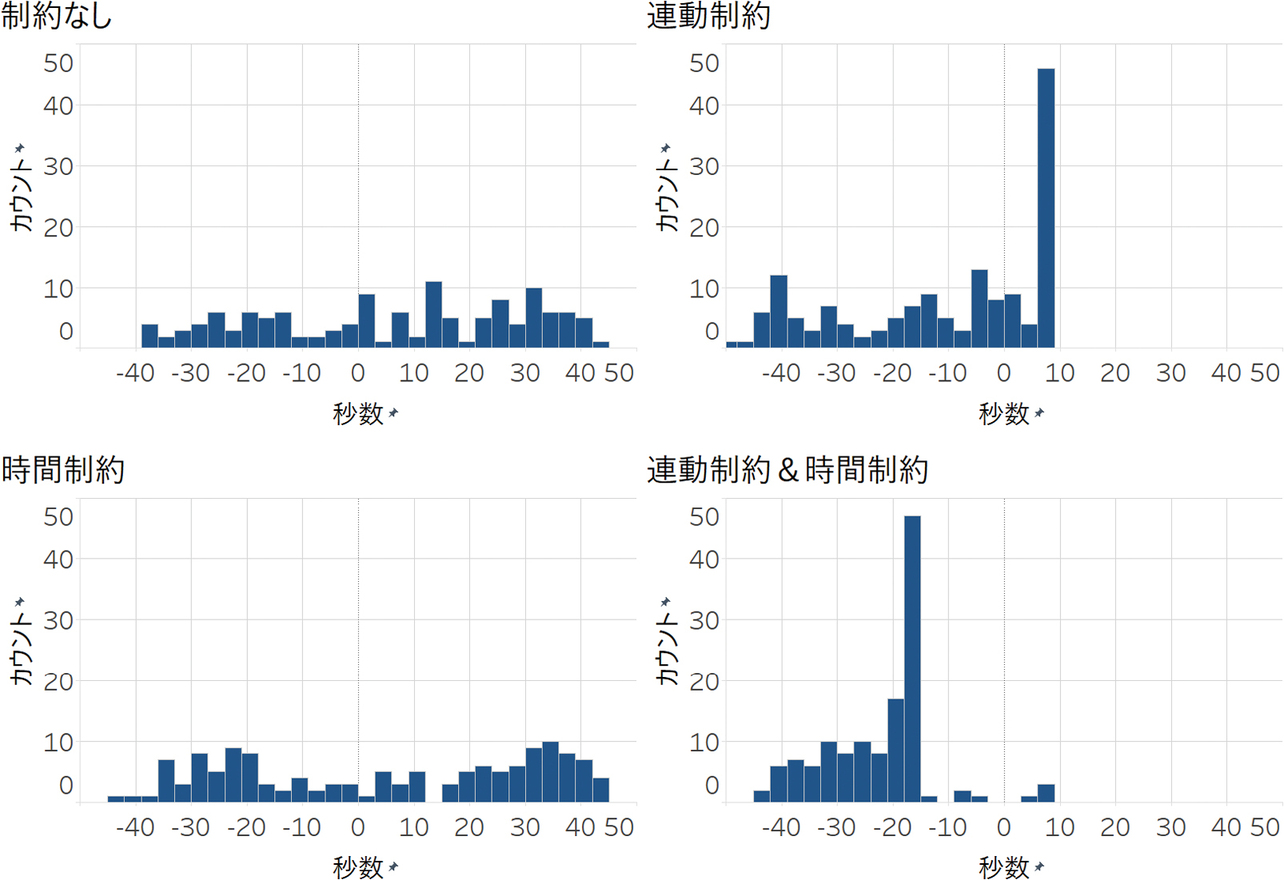
一方、連動制約は遅れ時間減少に効果がなかった、もしくは悪化させる結果となった。図5は右側交差点のサイクルを、図6は右側交差点の主道路青スプリットを、図7は中央交差点と右側交差点のオフセットをヒストグラムで表したものである。時間制約のみの場合、サイクルは70秒から80秒付近に、スプリットは60%程度に集中している。サイクルやスプリットを一定に保ちつつ、流量に合わせて現示時間の調整を適切に行っていることが確認できる。ただし、オフセットは一定ではなく、大きくバラついている。一方、連動制約を適用した場合、オフセットはある程度まとまったが、サイクルやスプリットが大きくバラついた。これは、中央交差点と右側交差点の連動が原因である。例えば、中央交差点の現示に追いつかれるのを待つために、既に車両が全て捌けているにも関わらず、右側交差点で青現示を続けてしまうことによる。その結果、サイクルが長くなり、渋滞を引き起こす。逆に、中央交差点の現示に追いつこうとすると、右側交差点のサイクルが短くなり、短時間での現示変更が強制される。特に従道路青信号が3秒で打ち切られることが多い。その結果、従道路に滞留車両が増加し、渋滞を引き起こす。強制的にオフセット協調を適用すると、サイクルやスプリットが大きく変動することで、全体として遅れ時間やCO2排出量が増加することが示唆された。
また、P1より流量が増加・減少したP2・P3では、定時間制御と比較して、時間制約つきの強化学習のほうが遅れ時間の増加幅が小さく、減少幅が大きい。これは、強化学習が突発的な流量の増加・減少に対してリアルタイムに現示時間を調整した結果と考えられる。青現示を延長することで滞留車両を減少させたり、車がいない場合に青現示を打ち切ったりすることで、遅れ時間の減少を実現したと推測する。
5. むすび
本研究では、まず、従来の強化学習によるサブエリア信号制御は、サイクルやスプリットが大きく変動し、実用的でないことを明らかにした。次に強化学習と交通工学を組み合わせ、現示秒数の制約を行うと、サイクルとスプリットが安定し、有効であることを示した。しかし、オフセットを同時式オフセットに固定し、信号同士を連動させる制約は効果がなく、むしろ結果を悪化させた。サイクルおよびスプリットに関しては、本制約は妥当であると考えられる一方で、オフセットに関しては、交通工学的な知見と整合する適切な制約とは言い難く、現時点では適切な状態・行動・報酬の設計が発見できていない可能性がある。オフセットを適切に制約した強化学習による最適な現示制御については、今後の研究課題とする。
本研究を通じて、交通工学と強化学習の融合による効果的な信号制御手法の可能性が示された。これは、交通渋滞の緩和や環境負荷の低減に寄与し、今後の交通システムの発展に大きく貢献すると期待される。
最後に、交通工学についてご助言頂いたオムロンソーシアルソリューションズ株式会社 交通ソリューション事業本部 事業開発部の大谷龍治氏、谷口弘師氏、また執筆においてご助言頂いたオムロンソーシアルソリューションズ株式会社 事業開発統轄本部 技術創造センタの金森祥太氏に感謝する。
参考文献
- 1)
- 国土交通省道路局. “WISENET2050.” 国土交通省. https://www.mlit.go.jp/policy/shingikai/content/001758738.pdf(Accessed: Mar. 26, 2025).
- 2)
- 警察庁. “第5次社会資本整備重点計画(警察関連部分)について.” 警察庁. https://www.npa.go.jp/bureau/traffic/seibi2/annzen-shisetu/institut/plan/pdf/juutenkeikaku.pdf(Accessed: Mar. 26, 2025).
- 3)
- 伊澤茉莉花, 山本健生, “複数の交通流量における深層強化学習を用いた信号制御の実験と考察,” 人工知能学会全国大会, 2023, セッションID 3Xin4-69.
- 4)
- K.-L. A. Yau et al., “A survey on reinforcement learning models and algorithms for traffic signal control,” ACM Comput. Surv., vol. 50, no. 3, pp. 1-38, 2017.
- 5)
- F. Rasheed et al., “Deep reinforcement learning for traffic signal control: A review,” IEEE Access, vol. 8, pp. 208016-208044, 2020.
- 6)
- 一般社団法人 交通工学研究会, 平面交差の計画と設計 基礎編: 計画・設計・交通信号制御の手引, 丸善出版, 2018, pp. 184-215.
- 7)
- V. Mnih et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, pp. 529-533, 2015.
- 8)
- M. Wiering, “Multi-agent reinforcement learning for traffic light control,” in ICML ’00: Proc. Seventeenth Int. Conf. Mach. Learn., 2000, pp. 1151-1158.
- 9)
- B. Abdulhai et al., “Reinforcement learning for true adaptive traffic signal control,” J. Transp. Eng., vol. 129, no. 3, pp. 278-285, 2003.
- 10)
- L. Li et al., “Traffic signal timing via deep reinforcement learning,” IEEE/CAA J. Autom. Sin., vol. 3, no. 3, pp. 247-254, 2016.
- 11)
- 佐藤季久恵 他, “Deep Q-Networkを用いた交通信号制御手法の提案,” 2017年度人工知能学会全国大会(第31回), 2017, セッションID 3I2-OS-13b-4.
- 12)
- 韓天陽 他, “予測深層強化学習の単独交差点信号制御への適用性に関する一考察,” 生産研究, vol. 73, no. 2, pp. 107-112, 2021.
- 13)
- 桑原雅夫 他, “強化学習を用いた信号制御パラメータ最適化に関する基礎的研究,” 第42回交通工学研究発表会, 2022, pp. 563-570.
- 14)
- H. Wei et al., “CoLight: Learning network-level cooperation for traffic signal control,” in CIKM ’19: Proc. 28th ACM Int. Conf. Inf. Knowl. Manag., 2019, pp. 1913-1922.
- 15)
- T. Nishi et al., “Traffic signal control based on reinforcement learning with graph convolutional neural nets,” in 21st Int. Conf. Intell. Transp. Syst. (ITSC), 2018, pp. 877-883.
- 16)
- Y. Wang et al., “STMARL: A spatio-temporal multi-agent reinforcement learning approach for cooperative traffic light control,” IEEE Trans. Mobile Comput., vol. 21, no. 6, pp. 2228-2242, 2022.
- 17)
- P. A. Lopez et al., “Microscopic traffic simulation using SUMO,” in 21st Int. Conf. Intell. Transp. Syst. (ITSC), 2018, pp. 2575-2582.
- 18)
- L. N. Alegre, “SUMO-RL.” GitHub. https://github.com/LucasAlegre/sumo-rl(Accessed: Mar. 26, 2025).
本文に掲載の商品の名称は、各社が商標としている場合があります。














