UHF帯RFID受信波形を活用した移動する荷物の
順序識別方法
今日の工場内物流は、多品種少量生産や商品の複雑化のため部品管理の重要性が増す一方、労働力不足という社会課題に直面している。これに対応するため、省人化を目指した作業の自動化が進められており、現場では資材や部品の管理システム機能の高度化が求められている。これらの要求に応えるため、特にUHF帯RFIDは、アンテナから数mから十数m先に離れて存在する複数のRFタグからの返信を一括して個別に読み取ることができるというメリットを持ち、トレーサビリティ確保の有効な手段として期待されている。一方で、現状のUHF帯RFIDの機能では荷物の存在を認識することはできるが、荷物が並ぶ順序を把握するといった機能は不十分である。
本論文では、汎用のUHF帯RFIDシステムで取得したRFタグの返信の時間波形とその波形の特徴を解析し、高精度にRFタグが貼られた荷物が並ぶ順序を識別する技術を提案する。実機評価にて、コンベア上を数百mmの間隔で順序良く流れてくる荷物の順番を把握するといった課題について、実用化に向けた有望な結果が得られた。今後、他のアプリケーションへの応用も期待される。
1. まえがき
近年、製造業界においては、製品の複雑化や高機能化、消費者ニーズの多様化に対応するため、多品種少量生産の導入が加速している。これに伴い、膨大な種類と数量の部品を管理する必要性が高まっている。また、少子高齢化による労働力不足という社会的課題も重なり、資材や部品の管理に関する人員の確保が困難になっている。このような状況下で、工場内物流、すなわち構内物流においては、省人化を目指し、コンベア上を流れる部品や資材の仕分け、倉庫内の在庫管理、倉庫の運搬口での入出庫管理といった業務の自動化が模索されている。とりわけ、資材や部品の管理システム機能の高度化が求められている。
これらの要求に応えるためには、設置型センサによる検知や、センサ搭載ロボットによる探索などで、正確に部品や資材が並ぶ順序を把握する機能の向上が有効である。これによって、後工程で機械による仕分け作業ができ、棚上の該当する資材や部品が入る箱を特定することで棚卸やピッキングの際の探索時間を減らすことができる。また、ゲートを通過する資材や部品の通過方向がわかれば自動で入出庫の判断が可能になる。
これに対して現状では、工場内でのトレーサビリティを確保する手段として、コードリーダやRFID(Radio Frequency Identification:無線周波数識別)といった個体識別システムが利用されている。なかでも、導入コストが低く、コードも作成しやすいため、一般的にはコードリーダが広く普及しているが、コンベア上を流れる荷物情報を読み取るようなケースでは、光学的にコードを読むことが必要なコードリーダは様々な方向から荷物に向けて設置するため、リーダの数が増える、設置時の調整に時間がかかるといった課題が存在する。
一方で、RFIDはLF(長波)帯、HF(短波)帯、UHF(極超短波)帯といった周波数帯が存在し、リーダライタ(R/W)とそれに接続されるアンテナで構成されている。しかも、RFタグも必要でコードリーダと比べ導入コストがかかる。しかしながら、UHF帯RFIDは、コードリーダやLF帯、HF帯といった他のシステムと比べても、アンテナから数mから十数m先に離れて存在する複数のRFタグからの返信を一括して読み取ることができるため、少ないアンテナの数で設置時の調整もしやすくなり、トレーサビリティ確保の有効な手段として期待されている。だが、現状のUHF帯RFIDの機能では、検出範囲内で荷物の存在を把握することはできるが、正確に部品や資材の並ぶ順序を把握することは難しい。したがって、我々はUHF帯RFIDに接続されたアンテナで、荷物に貼られたRFタグからの返信を一定期間蓄え、得られた時間波形のデータから所望の検出範囲内でRFタグが貼られた荷物の並ぶ順序を把握できるアルゴリズムを考案した。これにより、コードリーダでの課題であったアンテナの数や調整時間を低減しても、部品や資材の並ぶ順序を把握する機能を持たせることができ、コンベア上を流れる荷物情報を読み取るといった活用が可能となる。
本論文では、アルゴリズムの原理および適用した際の効果について報告する。本章に続く第2章では、前提となる想定ユースケースでの技術課題とその打ち手を説明する。第3章では本論文で提案する検出方式の原理と使用したアルゴリズムを紹介し、得られる効果についてシミュレーションにより妥当性検証した結果について述べる。第4章ではユースケースとしてコンベア上を流れる部品や資材の仕分けを想定した模擬環境を使用して移動するRFタグの時間波形データを実測し、アルゴリズムを適用したときの効果について述べる。最後に第5章ではあとがきとして今後の発展性と課題を示す。
2. 想定ユースケースでの技術課題とその打ち手
本論文では、構内物流および在庫管理の効率化を目指し、以下のUHF帯RFID適用のユースケースとその技術課題を想定している。例えば、コンベア上を流れる荷物をコンベア横に設置したアンテナで把握し、正確に仕分けして誤配送を防いだり、ロボットに搭載したアンテナで棚上の荷物を把握し、ピッキングや棚卸しでの探索時間を短縮したり、ゲートに設置したアンテナで荷物の移動方向を把握し、入出庫の判断ができるといったユースケースが想定される。
これらのユースケースにおける課題は、荷物の存在を把握するだけでなく、検出したい範囲内に配列する荷物の順番を正確に把握することである。これはアンテナから見たRFタグの距離とアンテナ前方を通過する時間を把握するという技術課題に置き換えることができ、これができれば、1台のリーダライタとアンテナで得られるデータから所望の範囲内を順次流れる荷物や、棚上に並んだ荷物の順番を把握することが可能となる。また、2台のリーダライタとアンテナを左右に並べ、それぞれから同一RFタグの通過時間の差を得ることで、移動方向と移動速度を把握することも可能となる。このような技術課題を解決するため、UHF帯RFIDでは複数のアレイアンテナの測角情報から測位する方式1)や測角情報と組み合わせて測位することが可能な周波数掃引時の位相データを利用した測距方式2)が提案されている。しかしながら、アレイアンテナはシステム規模が大きくコストがかかり、アンテナ寸法も大きくなるため実現性が低い。また、周波数掃引幅には国内電波法の制約があり、実現できる距離精度がおよそ1 mと低く、課題解決に至らない。したがって、ここでは1組のリーダライタとアンテナという小規模なシステム構成で実現でき、距離と通過時間をより高い推定精度で実現可能な方法を考える必要がある。我々はこれまで示した課題に対し、1組のリーダライタとアンテナでRFタグからの返信を一定時間検出した時間波形の特徴から距離と通過時間を推定する方法を提案し、課題解決への可能性を見極める。
本論文では、特にコンベア上を順次流れる荷物の仕分けというユースケースを対象とし、これらの課題を解決するための技術調査を進めた内容を示す。これにより、構内物流管理の効率化と自動化に貢献することを目指している。
3. 提案方法と効果の妥当性検証
3.1 原理説明
UHF帯RFIDは図13)に示す構成でRFタグからの返信をアンテナで受信し、リーダライタ内で送信信号と掛け合わせ、これをI(同相成分)とQ(直交成分)のデータとして出力し、式(1)を使いθ(位相データ)を算出する。
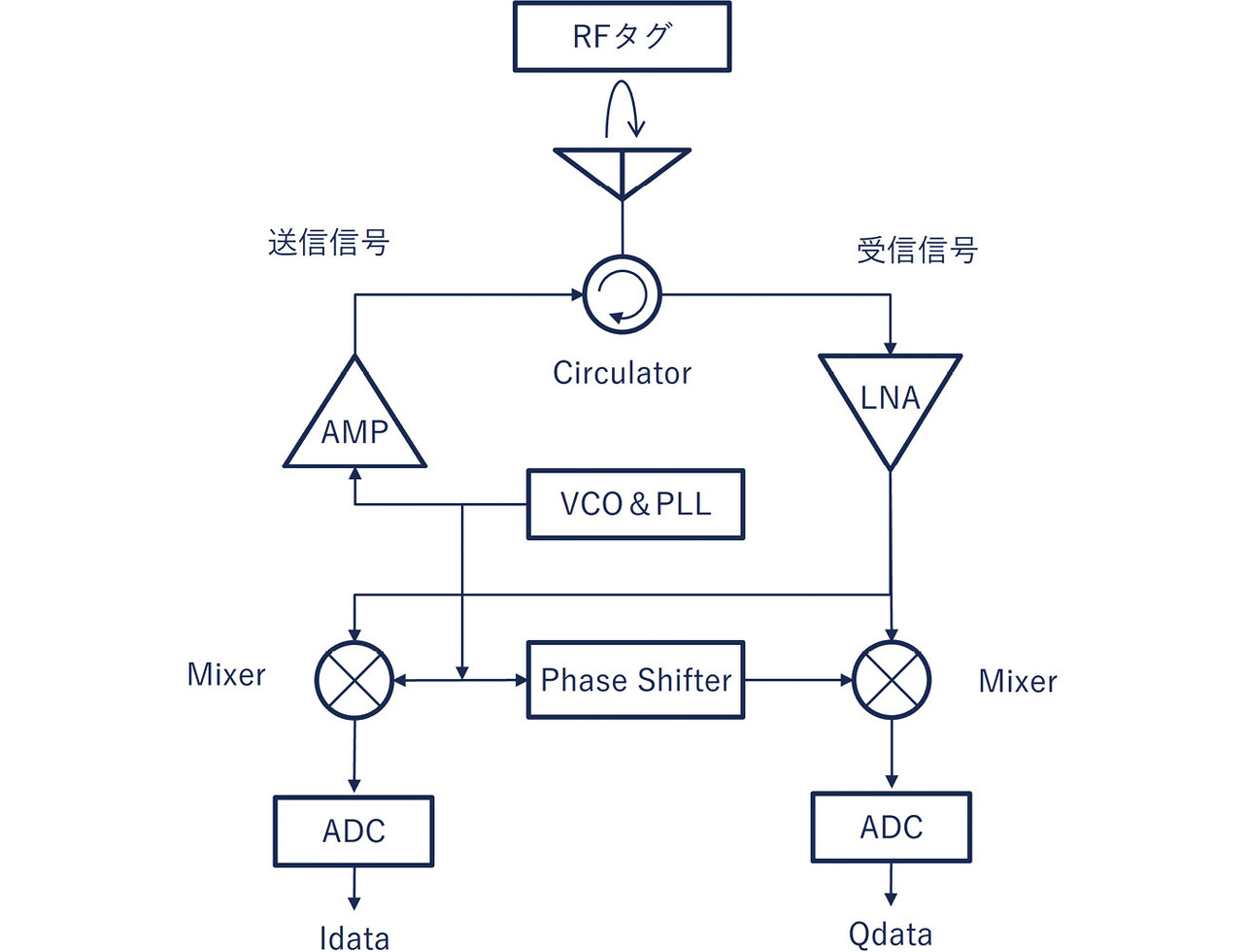
式(1)から、この受信した位相データは送信信号を基準とした受信信号の変化を表すため、RFタグとアンテナ間の距離に比例して変化する。
次に提案方法はこの位相データの時間波形の特徴からRFタグがアンテナ前方を通過する際の距離や時間を推定するものである。図2に示すようにRFタグはデータ検出開始位置をX0として、一定速度Vでアンテナ前方を横切るように移動している。RFタグが移動するときにはアンテナに接近するまで位相は減少し、アンテナ前方を通過した後、増加に転じる。なお、Xtag、YtagはRFタグの位置座標を示し、Xant、Yantはアンテナの位置座標を示す。さらにここから、RFタグの移動を検知する位相データは、次の式(2)で表すことができる。ここで、λは使用周波数における波長を表す。
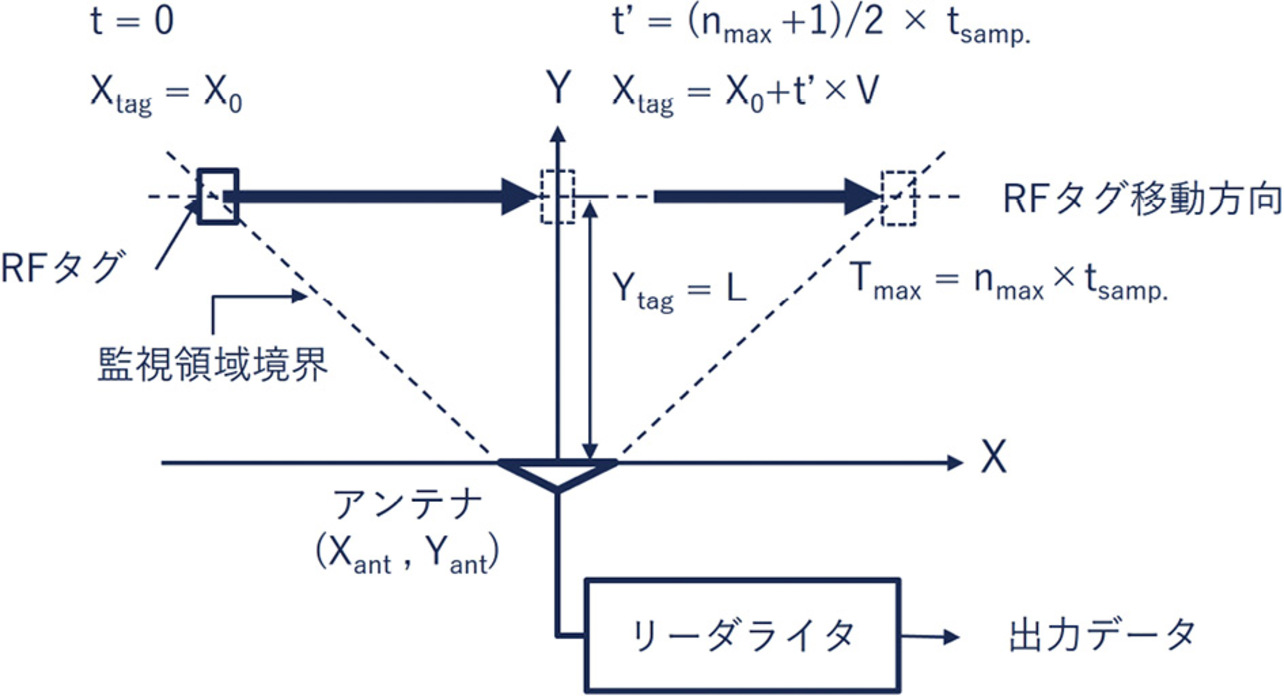
なお、この一連のながれは、式(3)(4)の条件を満たす。
ここで、tsampはデータサンプリング周期、nはサンプリング数を示す。
以上から、時間波形は谷型の波形を形成し、最短距離(、nmax は一定時間の計測で取得する最大のデータサンプル数)のときに位相が最小点となる。
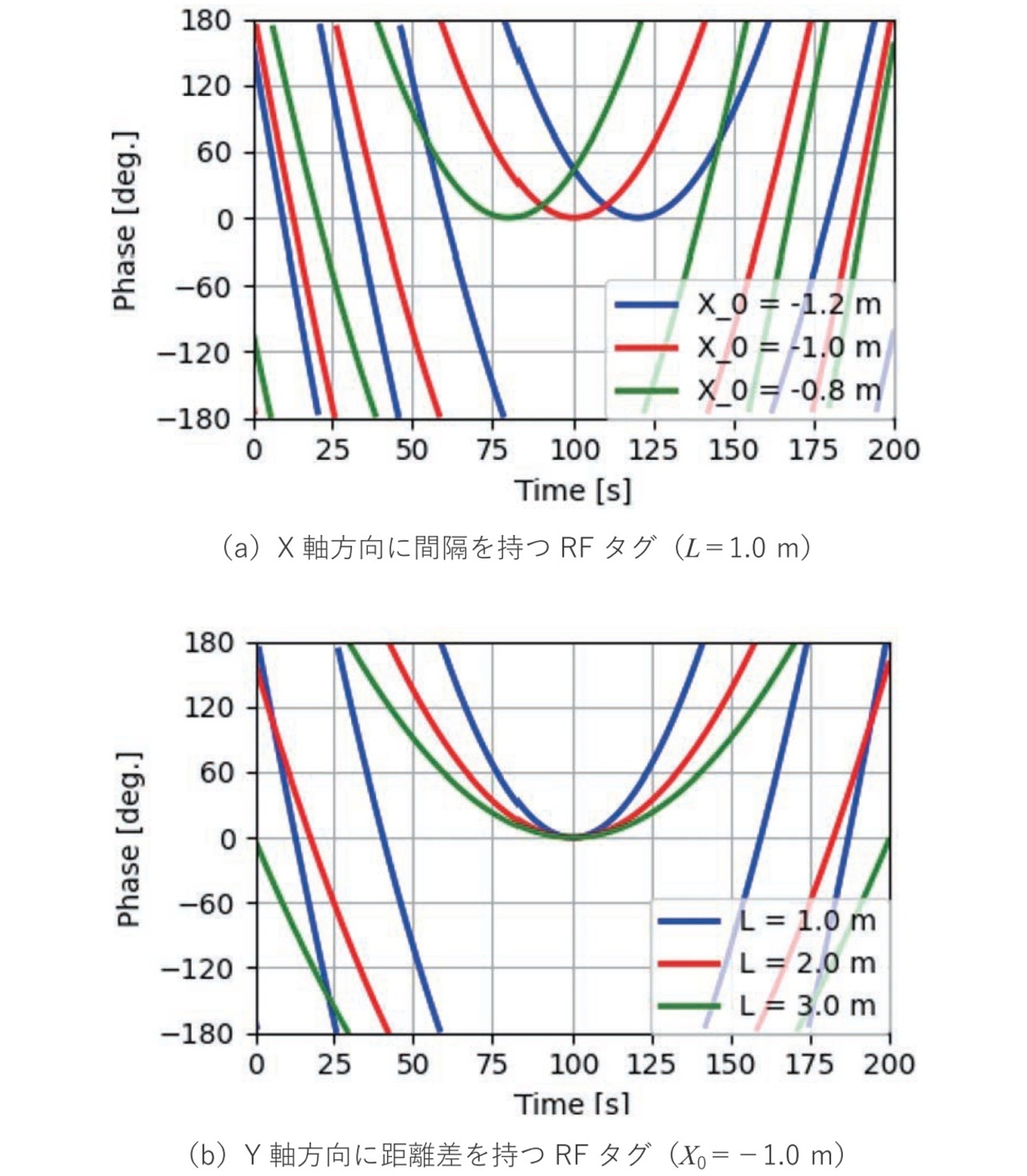
図3は、表1に示す計算条件に基づき、式(2)、式(3)、式(4)を使用して算出した理論的な位相データの時間波形であり、図3の(a)(b)の違いは、L を一つ代表例で固定し X0 を変化させたとき、X0 を一つ代表例で固定しL を変化させたときそれぞれの特性の変化を示している。
| パラメータ | 値 |
|---|---|
| 周波数:f | 0.91675 GHz |
| 波長:λ | 0.327 m |
| RFタグ移動速度:V | 0.1 m/秒 |
| アンテナ位置:(Xant, Yant) | Xant:0 m, Yant:0 m |
| RFタグ移動開始位置:(X0, Ytag=L) | X0:-1.2, -1.0, -0.8 m L:1.0, 2.0, 3.0 m |
具体的に図3(a)は、3つのRFタグのX0を20 cm間隔でずらし、移動させたときに得られる位相データの時間波形を示している。各RFタグの計測開始地点は X0:-0.8, -1.0, -1.2 mとしている。このとき、L:1.0 mで固定とし、条件に示した移動速度(0.1 m/s)を想定すると位相最小点をとる通過時間 t′ は8, 10, 12 秒となる。
また、図3(b)は最短距離Lを1.0 mから3.0 mまで1.0 mずつ変えた際の時間波形の変化を示している。このときX0:-1.0 mとし、通過時間t′ は10 秒となる。
各時間波形が作る谷形状の開き角はLが大きくなるにつれ拡がる傾向がある。これらの結果から、RFタグがアンテナ前方を通過する時間や最短距離により時間波形は判別可能な特徴を持つことがわかる。我々は、このように一定速度で移動するRFタグがアンテナ前面を通過する際に検出される時間波形の形状を解析し、最短距離Lと通過時間t′ を推定する方法を提案する。
3.2 提案する推定方法
提案するRFタグとアンテナの最短距離と通過時間の推定方法は、前節で示した表1のパラメータ条件で算出した時間波形をリファレンス波形とし、受信した位相データの時間波形と相関をとり、高い相関を示すときの通過時間や最短距離を推定値として示す方法である。図4に示すフローに従い処理を行う。ここでは例として表1に示す条件でRFタグ移動開始時間をX0:-1.0 m、L:1.0 mとおいたときの処理結果を例としてフローの内容を説明する。

移動するRFタグの返信を、検出開始から任意の点数以上となるまで連続して受信し、一定時間で取得した位相データをメモリに保存する(図4中1、2)。次に、最短距離と通過時間、既知のRFタグ移動速度と受信期間に基づいて図3に示した時間波形をリファレンス波形として算出する(図4中3)。この際、RFタグはもっとも単純なユースケースとして、アンテナからの電波放射方向と垂直方向に一定速度で移動するという条件で作成する。なお、リファレンス波形は事前に算出し、データベースを構築しておき、データ取得後に読みだして使用する形でも構わない。
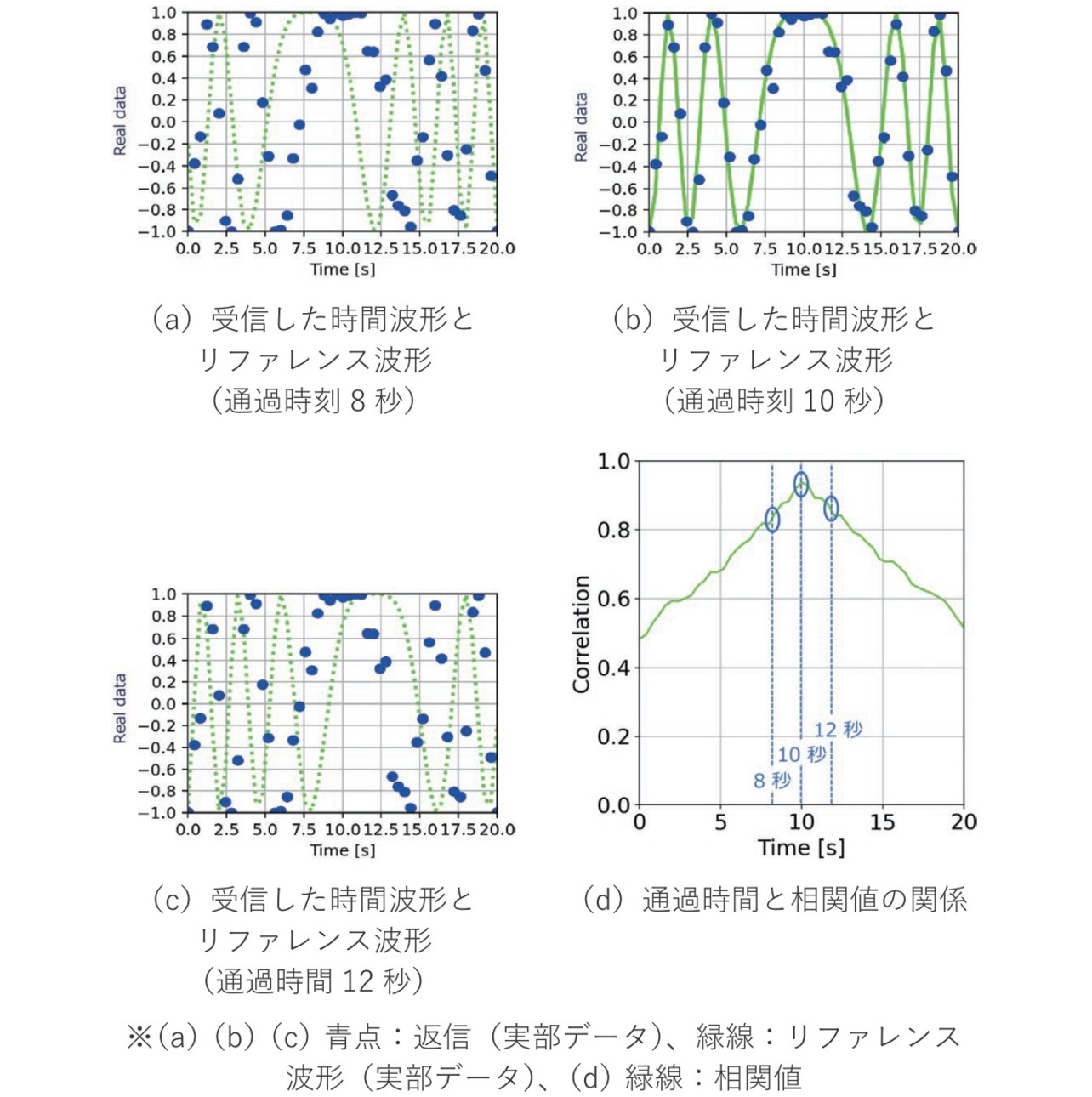
図5は通過時間を掃引したリファレンス波形と受信した波形の相関値が実際のRFタグの通過時間で最大となることを示している。図5(a)(b)(c)は、受信した時間波形とリファレンス波形を並べた図を示しており、通過時間を掃引しながら双方の波形の相関値4)を式(5)で算出し(図4中4)、得られた通過時間と相関値の関係を図5(d)に示す。
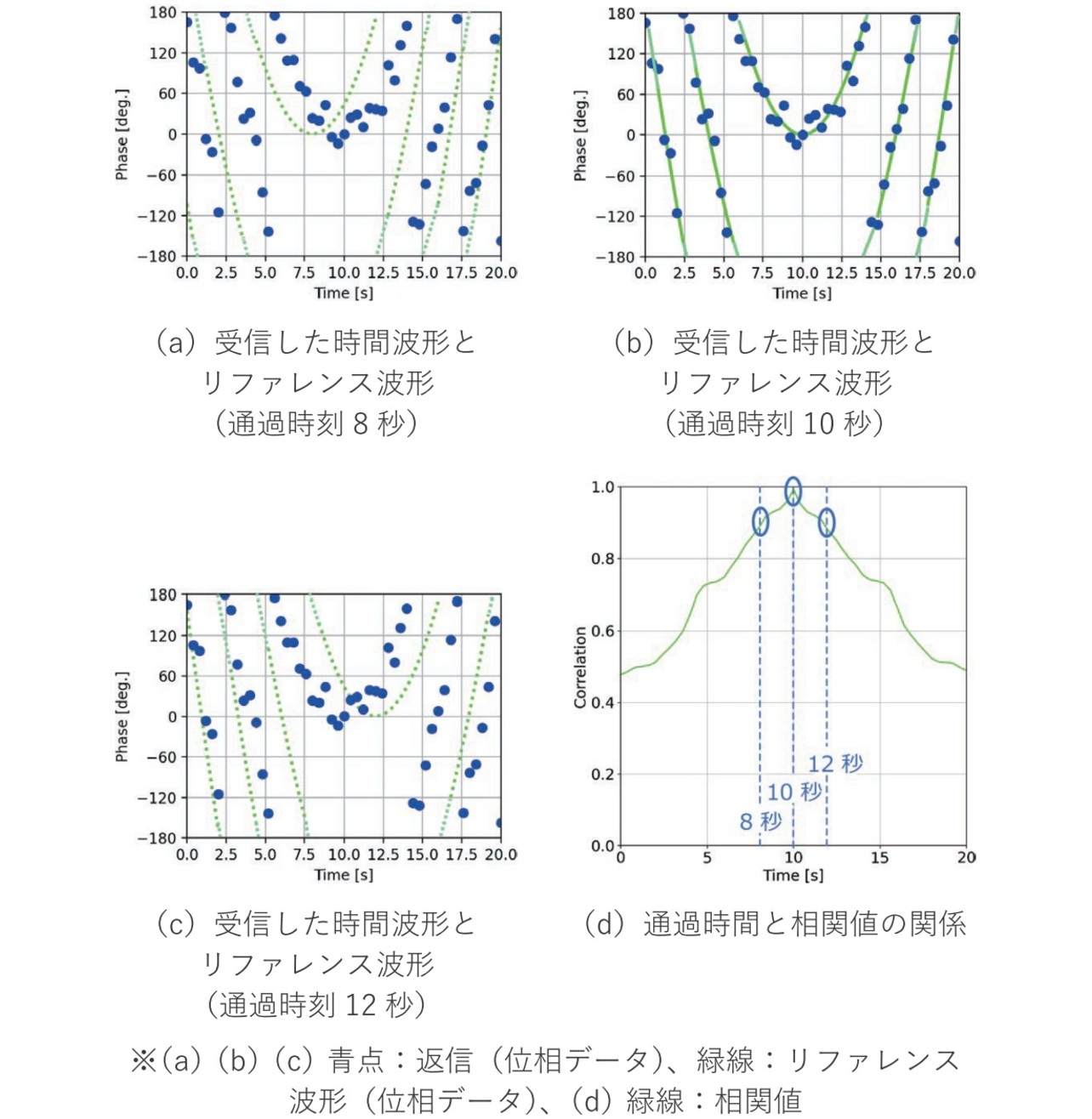
図中の相関値が最大となる通過時間が実際のRFタグの通過時間となる。結果から図5(b)に示す通過時間10秒のときの波形が最も受信データと相関が高い時間となることが確認できる。
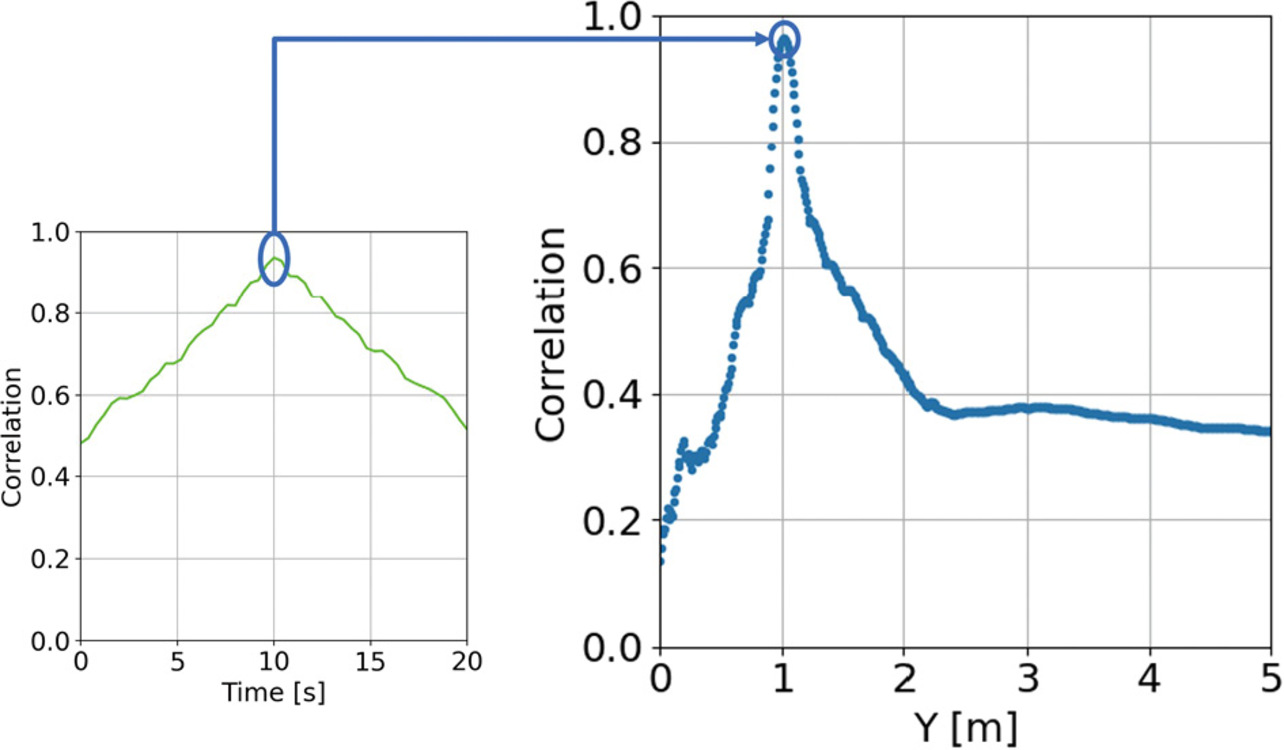
同様の処理を距離方向に掃引しながら行い、各距離で最大となる相関値を得る。そしてこの結果を距離毎に並べたグラフを図6に示す。最後に、相関値が最大となる距離と時間を抽出し(図4中5、6)、この値をRFタグとアンテナ間の最短距離と通過時間の推定値とする(図4中7)。ここまで示したフローにより、時間波形からRFタグとアンテナの最短距離と通過時間を推定することができる。
一方、ここまで利用していた位相データは図3、図5に示すように位相が±180度となる地点で位相が反転しデータが不連続となる現象(以下、折り返し)が生じる。これは図6の右図に示す距離方向(Y[m]で表示)の相関値に現れる不連続の要因となり、極端な相関の低下が見られる。この不連続をなくすため、原理的に折り返しが発生しない式(6)で算出される実部(Real)データもしくは虚部(Image)データの時間波形を利用することにした。
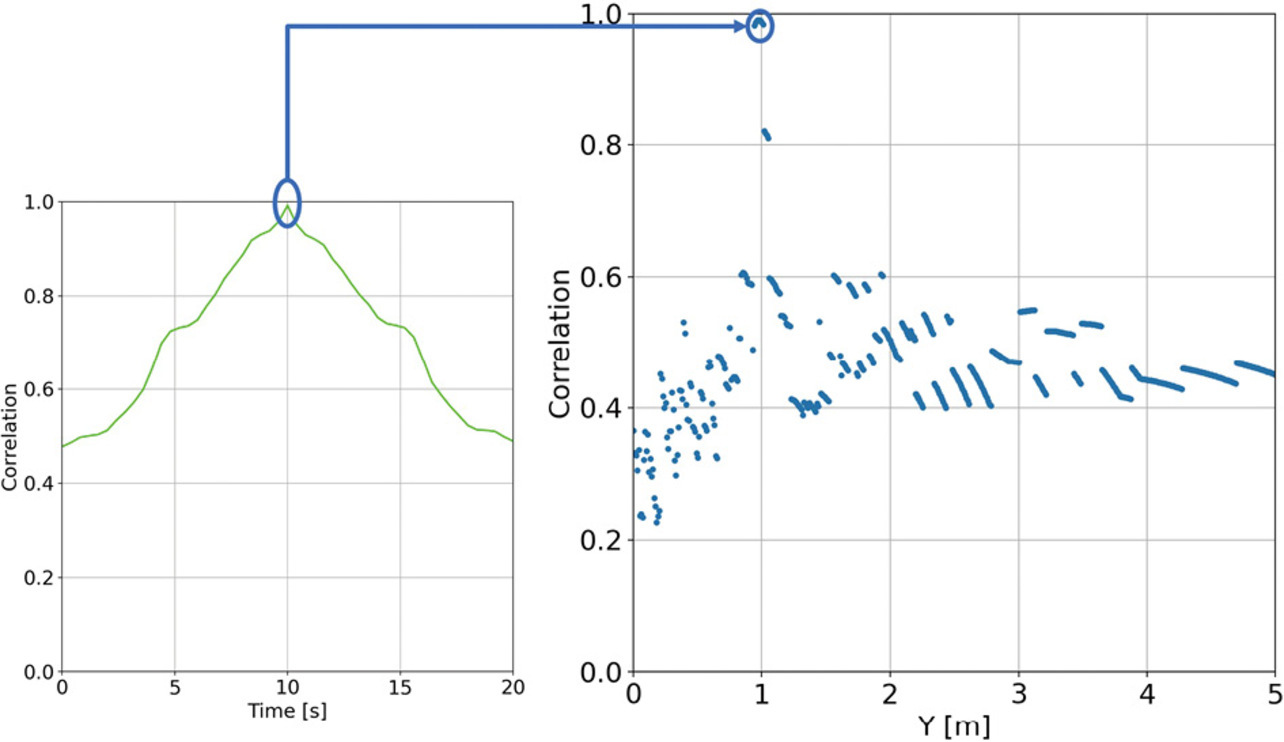
図7、図8は位相データを実部データに変更した時の計算結果であり、図7(a)(b)(c)に示すように実部データは折り返しが生じず、図8右図のように距離方向の相関値にも不連続が生じていない。よって推定精度低下のリスクが下がることが期待される。また、虚部データを使用した際も同様の効果が期待される。一方、位相アンラップ(制限された位相の範囲(通常0から360度、または0から2π)から、元の位相を復元する処理)5)により、位相データを折り返しのない連続データに置き換える方法もある。しかしながら、この方法は位相に誤差がある場合にアンラップの判断を間違えやすいデメリットがあり、この問題解決のために追加処理が必要となり複雑である。そのため、本方式では比較的処理がシンプルな実部データもしくは虚部データを利用する方式を選択する。
3.3 推定精度の比較
ここで、表2に示す条件で受信された位相データおよび実部データから推定した結果を比較する。ここでは推定処理の効果比較が目的のため、式(7)のように位相誤差(Phase Error、標準偏差:5、10、15度のランダムな誤差)を加算した位相データ、およびこの位相データを実部データに変換したデータを使用する。3種類の誤差を用いたデータの比較を行った結果として、最短距離L 1 mでの通過時間と最短距離の推定精度を表3、表4に示す。また、推定結果をグラフ化し図9、図10に示す。同一条件で100回の推定を試行したときの推定誤差の平均値と標準偏差を算出した。
| パラメータ | 値 |
|---|---|
| 周波数:f | 0.91675 GHz |
| 波長:λ | 0.327 m |
| RFタグ移動速度:V | 0.1 m/秒 |
| サンプリング時間:tsamp. | 0.4 秒 |
| 最大サンプル点数:nmax | 51 |
| アンテナ位置:(Xant, Yant) | Xant:0 m, Yant:0 m |
| RFタグ移動開始位置 : (X0, Ytag=L) |
(-1.0 m, 1.0 m) |
| 位相誤差 | 標準偏差 5、10、15度 |
| 位相誤差(度) | 推定精度 | |||
|---|---|---|---|---|
| 時間精度(秒) | 距離精度(m) | |||
| 平均 | 標準偏差 | 平均 | 標準偏差 | |
| 5 | -0.01 | 0.11 | -0.02 | 0.02 |
| 10 | 0.16 | 0.89 | -0.02 | 0.13 |
| 15 | 0.03 | 1.80 | 0.09 | 0.42 |
| 位相誤差(度) | 推定精度 | |||
|---|---|---|---|---|
| 時間精度(秒) | 距離精度(m) | |||
| 平均 | 標準偏差 | 平均 | 標準偏差 | |
| 5 | 0.00 | 0.00 | -0.02 | 0.02 |
| 10 | 0.00 | 0.04 | -0.05 | 0.03 |
| 15 | -0.08 | 1.71 | -0.01 | 0.37 |
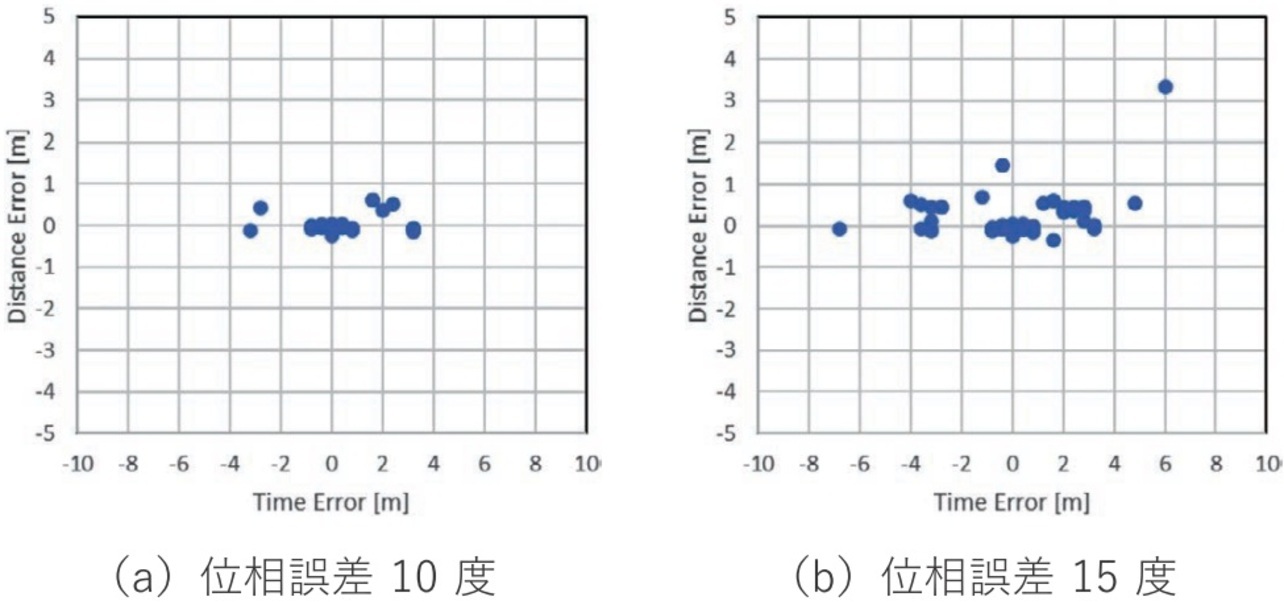
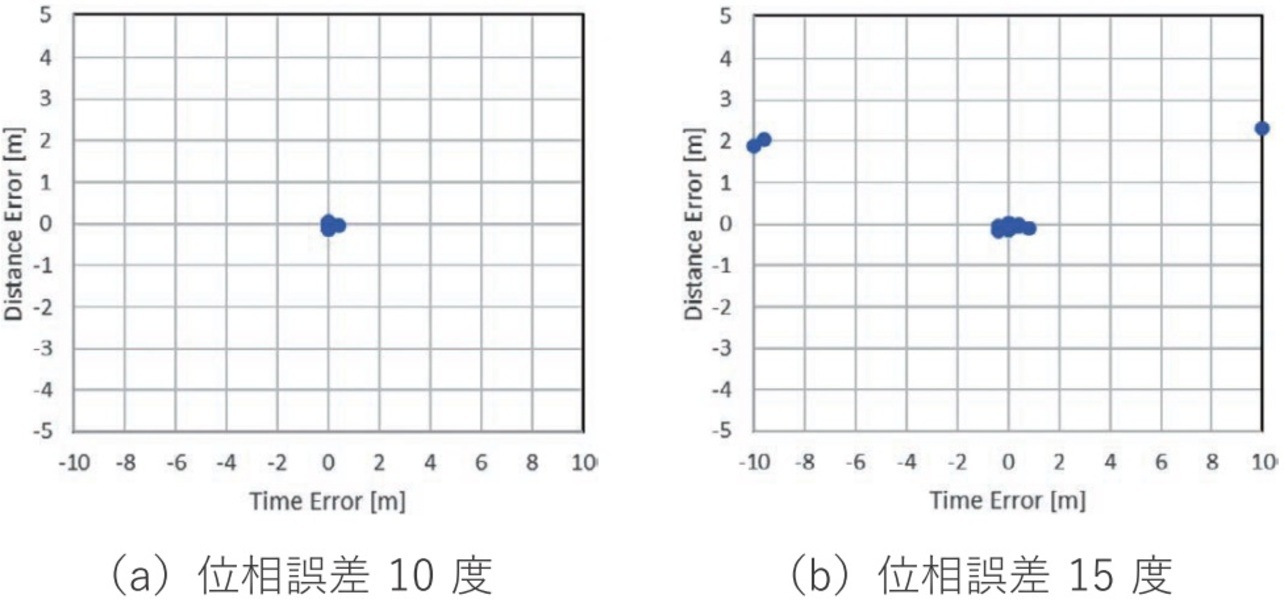
結果から誤差の平均値、標準偏差ともに位相データに比べて実部データを使用した方が精度向上する効果が得られ、実部データを利用することの有効性が示された。一方で、位相誤差が15度以上では実部データ使用時でも推定誤差が数 m、数秒と大きくなる場合も見受けられる。これは正となる通過時間と最短距離での相関値が低下し、他に高い相関値となるポイントを推定値として拾っていることが要因と考えられる。実環境で位相誤差が大きくなる場合にはアンテナ位置調整で位相誤差を低減する、複数のアンテナでの検出や距離の観測範囲を設ける等の精度向上策を講じる必要がある。
4. 提案方法の効果検証
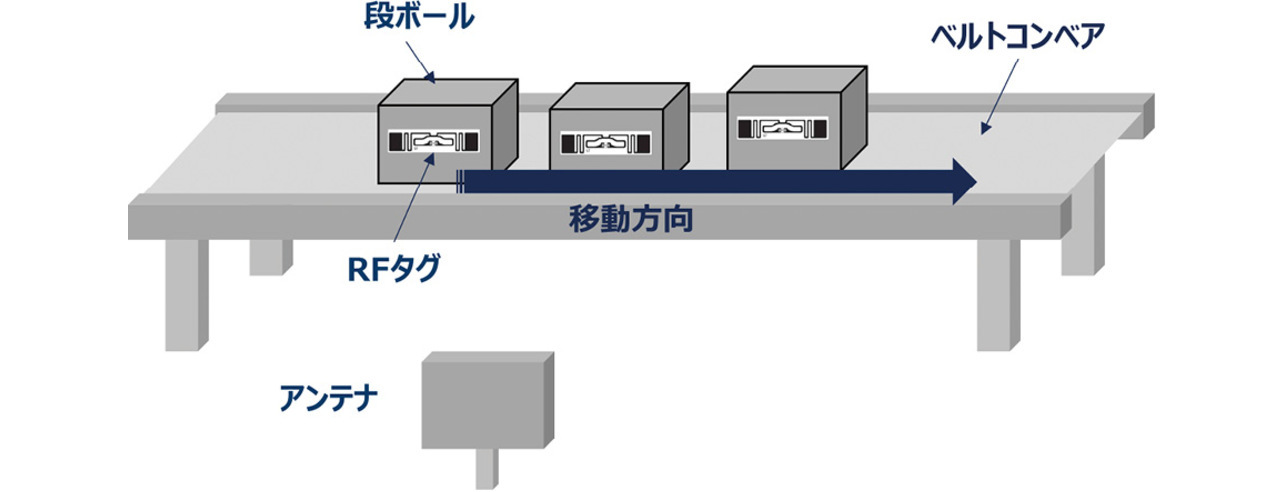
4.1 模擬環境評価
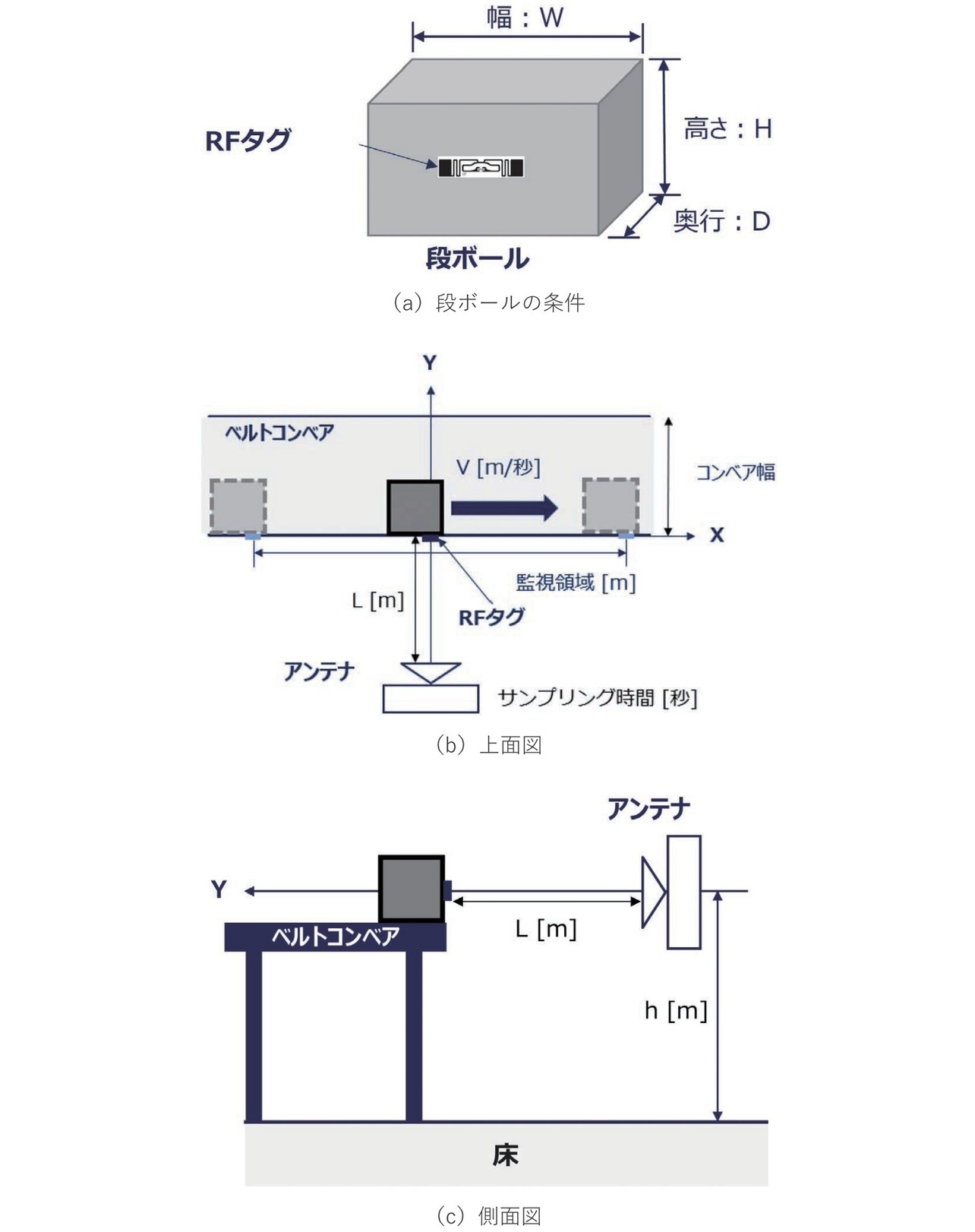
第3章で確定した方法の有効性を評価するため、図11に示すようなコンベア上を順次流れる荷物の仕分けというユースケースに基づき、図12に示すように、固定アンテナの前をRFタグが横切る形で、模擬環境を構築した。監視対象は、側面にRFタグを貼り付けた段ボール箱とし、これをコンベア上に配置し、一定速度で移動させた。使用したアンテナおよびコンベアの動作条件を含む評価条件は、表5に示す通りである。
| パラメータ | 値 |
|---|---|
| 周波数:f | 0.91675 GHz |
| 波長:λ | 0.327 m |
| RFタグ移動速度:V | 0.1 m/秒 |
| サンプリング時間:tsamp. | 0.4 秒 |
| 最大サンプル点数:nmax | 51 |
| アンテナ位置:(Xant, Yant) | (0, 0) |
| RFタグ移動開始位置 : (X0, Ytag=L) |
(-1.0 m, 1.0 m) (-1.0 m, 3.0 m) |
| 設置高:H | 0.75 m |
| 段ボール箱サイズ | Box W:390 mm Box H:200 mm Box D:290 mm |
| アンテナ偏波 | 右旋円偏波 |
| RFタグ偏波 | 水平偏波 |
4.2 評価結果
① 提案方法の効果確認
RFタグのアンテナ性能に影響のない空の段ボール箱にRFタグを貼り付けて実機評価し、提案方法の実現性を確認した。図12(a)には使用するRFタグ付き段ボールの条件を示し、図12(b)、図12(c)に示すアンテナと段ボールの位置関係にて距離Lを1 mおよび3 mにした際の検出結果を表6に示す。実部データを利用した実測結果は第3章で得られた精度と一致しており、効果を確認できた。
| 設置距離 | 推定精度 | |
|---|---|---|
| 距離精度 | 通過時間精度 | |
| 1 m | 0.01 m | 0.00 秒 |
| 3 m | -0.04 m | 0.00 秒 |
② 一般的な荷物を想定した際の推定
次に、一般的な荷物の条件として、表7, 図13に示すように段ボール箱の内容物、位置、回転といった状態を模擬し計測を行った。なお、内容物は水が満たされたペットボトルや、金属の箱を想定しており、段ボール箱の中全体を埋めている。但し、内容物は段ボール箱に貼り付けられたRFタグから1 cm程度隙間を開けた状態で固定されている。
| 荷物条件 | 内容物 | 向き | 位置 |
|---|---|---|---|
| 条件A | 空 | アンテナ対向 | 中央 |
| 条件B | 金属 (タグとの間隔有) |
アンテナ対向 | 前面 |
| 条件C | 水 (タグとの間隔有) |
進行方向向き | 前面 |
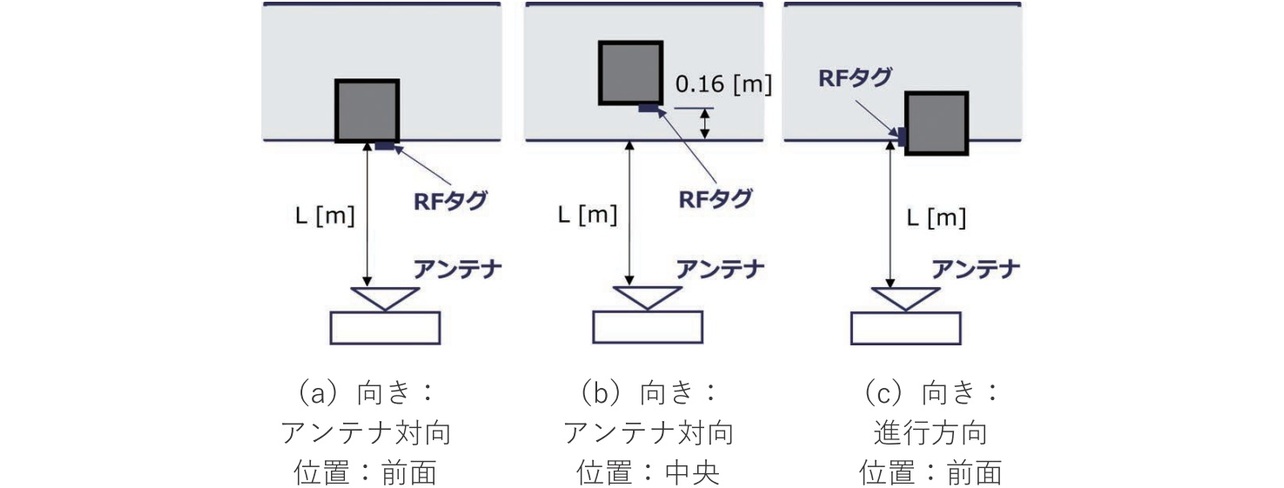
隣接するRFタグ間の間隔は図11に示すように隣り合って並び、表5に示す荷物(段ボール箱)の1辺の寸法から200~390 mmとなる。
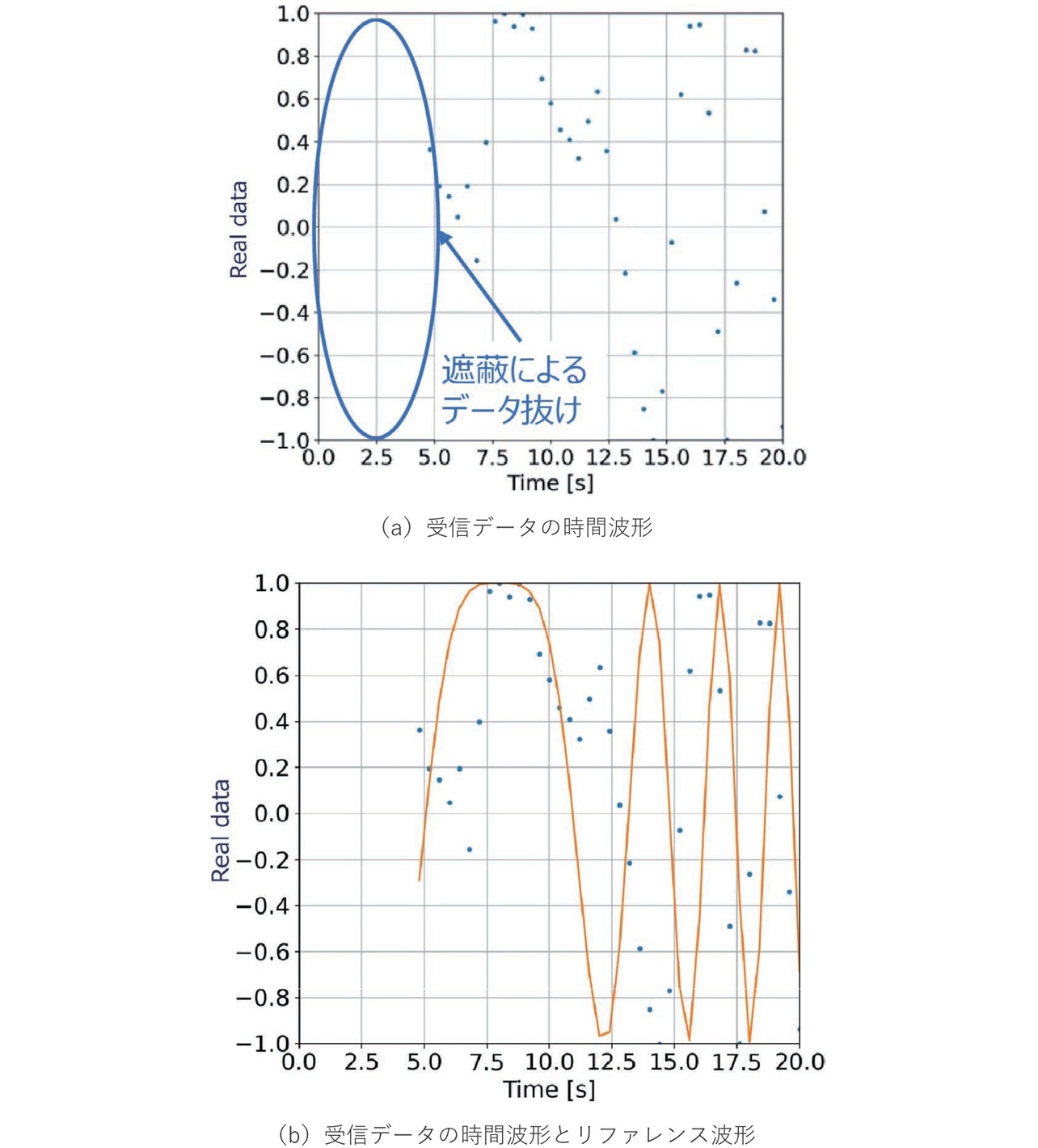
推定結果は表8に示すように、距離方向では120 mm、時間方向では2秒(200 mm相当)の精度で推定でき、流れる箱の順番を把握するといった課題について有望な結果が得られた。特に表7の条件Cにおいては図14(a)に示すように荷物による遮蔽で途中までデータが無い状態であり、内容物からの反射による誤差が含まれ、推定困難と思われるケースでも図14(b)に示すように推定できる可能性が示された。
| 荷物条件 | 推定精度 | |
|---|---|---|
| 距離精度 | 通過時間精度 | |
| 条件A | 0.06 m | 0秒 |
| 条件B | 0.12 m | 0秒 |
| 条件C | 0.03 m | 2秒 |
ただし、この評価条件と結果は一例であり、具体的なユースケースで考えられる条件に合わせ効果を確認することが必要である。また、これまでの測定は比較的広い実験室内で実施しており、壁などの反射物からは数mの距離をとった状態で実施しているため、マルチパスの影響は比較的緩和された環境である。したがって、今後は、より複雑な反射環境下での評価を進めることも求められる。
5. あとがき
本論文では、汎用のUHF-RFIDシステムで取得したRFタグの返信の時間波形とその波形の特徴からアルゴリズムによって高精度にRFタグの並ぶ順序を識別する技術の構築を目指した。結果として、実機評価にてコンベア上を数百 mmの間隔で順序良く流れてくる荷物の順番を把握できることを確認し、課題解決に向けた可能性を示すことができた。
また、提案方法は他にも以下のアプリケーションへの展開が可能である。
- アンテナ自身を荷物の前方を横切るように移動させることにより、棚上に配列された荷物の順番を把握するアプリケーション。
- 入出庫ゲートにアンテナを固定して計測することにより、ゲートを通過する荷物の移動方向を把握するアプリケーション。
したがって、この技術により高精度な荷物の並ぶ順序を認識できることで構内物流におけるプロセスの最適化が図られ、業務の効率化やコスト削減が実現できる可能性がある。
一方で、現状では理想に近い模擬環境での評価に留まっているため、実際の現場環境で生じるマルチパスのような課題については別途考慮が必要である。今後の課題としては、実際の物流現場での評価を進め、技術の実用化に向けたさらなる改良が求められる。特に、現場特有の環境要因に対応するための技術的な工夫や、システムの安定性を向上させるための研究が必要である。これにより、資材管理のさらなる効率化と精度向上を目指すことができると考えられる。
参考文献
- 1)
- S. Azzouzi et al., “New measurement results for the localization of UHF RFID transponders using an Angle of Arrival(AoA)approach,” in 2011 IEEE Int. Conf. RFID, 2011, pp. 91-97.
- 2)
- R. Miesen et al., “Phase based multi carrier ranging for UHF RFID,” in 2012 IEEE Int. Conf. Wireless Inf. Technol. Syst.(ICWITS), 2012, pp. 1-4.
- 3)
- 荒井雅行, “RFIDリーダの技術と課題,” 電子情報通信学会 通信ソサイエティマガジン, vol. 2008, no. 7, pp. 44-50, 2008.
- 4)
- 辻義之 他, “相関とスペクトル解析,” J. Plasma Fusion Res., vol. 85, no. 9, pp. 620-630, 2009.
- 5)
- 奥山哲, “ブランチカット法で生じた SAR 干渉画像中のアンラップエラーの修正, ” 測地学会誌, vol. 56, no. 4, pp. 149-153, 2010.
本文に掲載の商品の名称は、各社が商標としている場合があります。














