A Machine Learning System that Adaptively Aggregates Knowledge from Multiple Models
As a machine learning framework, decentralized learning aims to address the difficulties of data collection and annotation by breaking down and assigning these tasks to a group of clients to utilize their own data resources. Federated learning is a conventional approach of decentralized learning, but it is not suitable to deal with cases when the client model architectures or data distributions are diverse. This article introduces one of our published research results, which is a method called Decentralized Learning via Adaptive Distillation (DLAD). As a method based on knowledge distillation, it learns a model by aggregating and imitating the client models’ outputs, without requiring identical client-model architecture. Moreover, this method casts adaptive aggregation weights to different clients, to give priorities to learn from client models with higher confidence. This approach is especially useful for the non-IID (Independent and Identically Distributed) data. We have conducted evaluation experiments on multiple public datasets and demonstrated the effectiveness of this method.
1. Introduction
The content of this article is based on our recent paper named “Adaptive Distillation for Decentralized Learning from Heterogeneous Clients”1). In this article, the author would like to provide a reader-friendly explanation of the original paper. The purpose is not only to explain the details of technology, but more importantly, to give readers an insight that how to use the related technology to solve real-world problems, since knowledge deserves to be understood and utilized, to contribute to the business, and the world.
In current days, machine learning is undoubtedly a promising technology not only in academic research but also in enterprises. The most common difficulty to deploy machine learning in a real-world project is related to data, which is usually two-fold. First, deploying machine learning can be costly due to data collection. Some sensitive data, such as life logging videos, and medical data, that their owners wish to keep private, are hardly accessible. Second, deploying machine learning can be costly due to data annotation. Supervised machine learning (the most commonly used machine learning algorithm) requires that to learn a model, training data must be annotated with ground truth labels. Depending on the difficulties of tasks, annotation sometimes needs certain levels of professional know-how (e.g., a doctor’s diagnosis), and thus can be extremely expensive.
So, is there a method to alleviate the cost of data collection or data annotation? One promising solution is Decentralized Learning, which means to put the data collection and data annotation processes on the client side. Here, “client” usually means some institutions, companies, or end-users who are supposed to conduct data collection and data annotation as their daily behaviors (for comparison, we call the other side “server side”). For example, Google developed a machine learning model to predict the next word of the keyboard input2), and the data collection and data annotation are all performed by smartphone users’ daily keyboard input. It is important to note that, during the above process, end-users train their own prediction models on their devices, and only transfer model weights with Google, but not any sensitive data they have input using their smartphone keyboards. This decentralized learning framework is called Federated Learning (FL)3,4).
To better understand the advantages of decentralized learning, we give another example. Let us assume that OMRON is about to develop a new cardiac diagnostic device. It can help early detection of heart diseases by reading and analyzing users’ vital signs. Usually, the development of such a device would face a high hurdle because vital signs are sensitive and private data, and annotations need expertise from doctors. With FL, OMRON just needs to deploy the copies of their machine learning model to different hospitals, and get the models trained with the daily medical data. At the hospital (client) side, operators only need to input patient data (vital signs, profiles, etc.) and corresponding diagnosis into the model. Since the model neither uploads any private data to the OMRON side nor requires doctors to make additional diagnoses beyond their daily work, the difficulty of development is greatly reduced.
From the above example, FL is a promising decentralized learning framework and should be encouraged to use in practice. However, some limitations of FL still exist, for example:
- 1.
- FL requires client model architectures to be identical. Usually, it is applicable to just deploy the same model to all the clients. However, this requirement is inconvenient under some practical circumstances, such as that, clients may have needs of model customization (due to limitation of computational resources, privacy policies, performance bias, etc.); clients may already have their own trained models and we want to directly use them, and so on.
- 2.
- FL requires frequent data communication during the model training process. Although such data communication does not involve private data, the data communication itself also brings limitations and concerns, such as network qualities, securities, and so on. Also, if different clients have different communication conditions, it will be a problem to balance the training process among all the clients. Extra efforts are needed to improve the communication efficiency5,6).
In this article, the author would like to introduce another decentralized learning framework that is based on knowledge distillation (KD). It can solve the above issues that FL is not good at. Moreover, the proposed method uses an improved weight aggregation strategy to deal with the non-IIDness problem, which will be explained later. One should note that the KD-based decentralized learning framework is not necessarily superior to FL-based. One should be able to identify which framework is more suitable for their practical applications.
2. Method
2.1 What is knowledge distillation?
Knowledge distillation7) is a method that allows one trained model (the source model) to “teach” another new model (the target model). In other words, it allows a new model to imitate the output of an existed model, without significant loss of performance. The original purpose of KD is mainly on model compression, which means that, usually, the source model is a large (deep) model, and the target model is a small (shallow) model which is less expensive to be deployed in practice.
The reason a small model can approximate a large model in its performance is that, firstly, a large model usually has some excessive capacity or power which is not fully utilized; secondly and more importantly, a target model can benefit from learning “soft labels” from a source model. We will use an example to explain the latter one.
Consider an image classification task, where one of the images illustrates a cat playing with a mouse (see Fig. 1). Usually, the label (ground truth) will be “cat” only, since the cat occupies the main body of the image (it is theoretically possible but too ambiguous and inefficient to annotate this image as “cat and mouse”). In this way, the information of the mouse will be missing from the true label, and thus the machine learning model that learns from the true label will only learn “this image is showing a cat but nothing else”, which is actually not ideal.

On the contrary, in a KD scenario, the source model provides “soft labels” rather than true labels. Assume that the source model is well-trained (i.e., it can at least recognize cat and mouse precisely). Then in this case the model may produce a classification output like “70% cat, 30% mouse”. Unlike a true label that only represents one possibility, a soft label will represent all the possibilities in ratios. As a result, it can handle the cases such as “A and B are in the same image” or “this object looks like both A and B”, where the true label cannot. In KD, while the target model learns from soft labels (and from true labels, at the same time), it has been proved that it can perform better compared with only learning from true labels.
2.2 How does knowledge distillation benefit decentralized learning?
As mentioned previously, the original usage of KD is mainly about model compression, but KD can also benefit decentralized learning. In a KD-based decentralized learning framework, the client side owns source models, and the server side owns a target model. The client side trains source models with their private data and annotations, while the server side needs to collect its own data and input them to source models to get output (soft labels). After that, the server side trains the target model with its own data, and the corresponding soft labels which are aggregated from all the clients.
KD-based frameworks do not have the limitations of FL-based frameworks mentioned in the previous section. First, KD does not aggregate model weights but soft labels, so there is no need to keep model architectures identical. Any client or server can have a unique model. Second, there is no frequent data communication during the training process. Actually, the data communication only occurs twice: once for the server sending data to the clients, and the other for the clients sending soft labels to the server. The training processes (both on the client side and the server side) can be totally off-line.
KD also has its own limitations. During the above process, there is no data transfer from the client side to the server side, so the data privacy of the clients is protected, however, there is data transfer from the server side to the client side, which means the server side still need to collect enough data. Also, there is no need to annotate the server-side data by human labor, instead, the annotation is done by client-side models. Asking the clients to run their models may still incur costs. Compared with FL, requiring data collection may be a main limitation of KD, however, for some types of tasks, it is not so difficult to get unlabeled data, while sometimes the model heterogeneity can be a critical advantage.
2.3 How does our work differ from traditional knowledge distillation?
When we distill knowledge from multiple sources, there is no guarantee that all the sources provide outputs of the same quality. Different sources are likely to have different confidences towards different categories of samples. Here, the confidence may be due to many factors, for example, model architecture, annotation qualities, number of training data samples, and so on. Among them, the number of training data samples (on certain categories) is a very common factor caused by data distribution.
Traditional decentralized learnings, both FL-based and KD-based, aggregate the output (model weights or soft labels) evenly from multiple clients. It means that it does not distinguish which client gives a more trustable output and train with a bias accordingly. It is fine for IID (Independent and Identically Distributed) data. But in most cases, real-world data are non-IID. For example, patient data distribution will be diverse depending on regions, seasons, hospital categories, and so on. For the case of non-IID data, it is highly possible that some clients have never seen some categories of data samples during their training processes, and thus cannot provide confident outputs.
In our work, we proposed an improved KD method, Decentralized Learning via Adaptive Distillation (DLAD). It allows the target model to selectively learn from source models, which is an effective solution to non-IID data.
2.4 The details of DLAD
In our distillation process, for each data sample sent from the server to the clients, we not only expect to get an output from each client model but also want each client model can provide a confidence estimation, which represents “how confident am I to correctly classify this sample”. In our scenario, this condition is simplified to “how familiar is this sample to me” to address the issue of non-IIDness. It is rather tricky to let client models report their familiarity or confidence. Here we introduce our implementation as follows.
Fig. 2 shows the overview of the proposed DLAD framework. In the figure, D1 ⋯ DN represents the data owned by clients, M1 ⋯ MN (in black) represent the client-side models and orange ones are their binary copies (explained later), Ddist represents the data collected by the server side, and M represents the model owned by the server side.
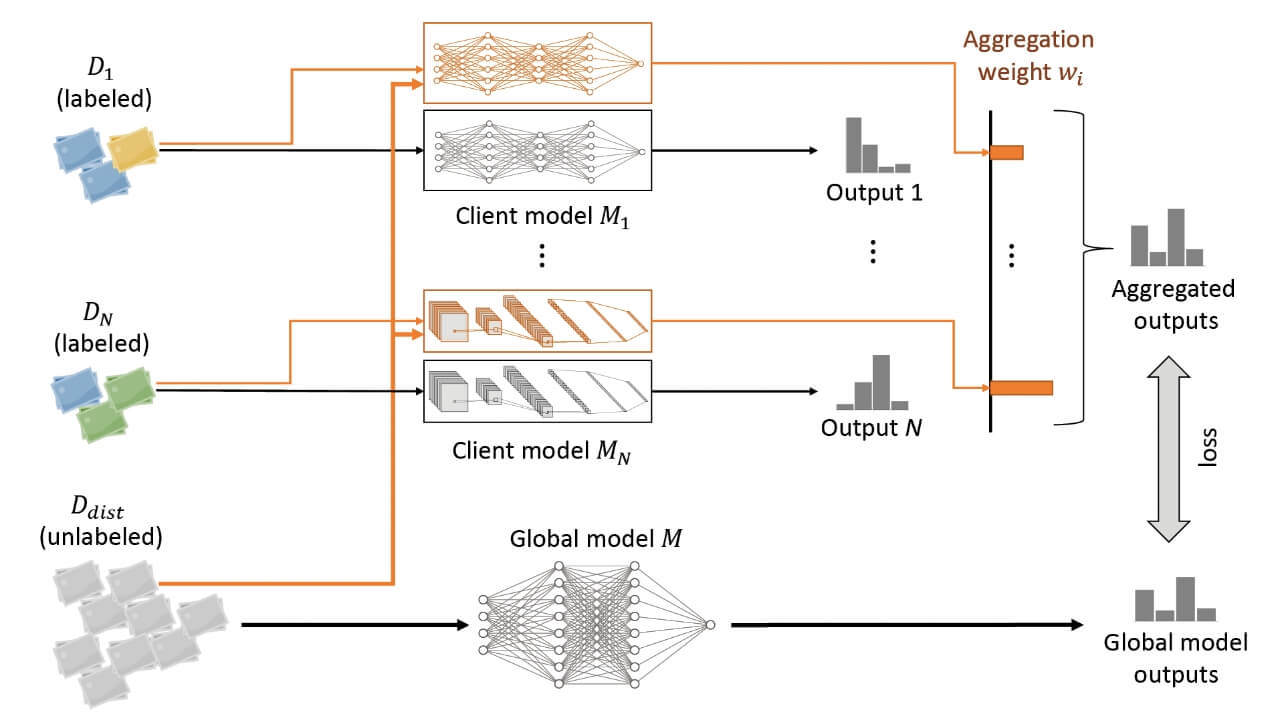
The training of DLAD has three steps.
Step 1, training client models. Clients train models M1 ⋯ MN with their own data D1 ⋯ DN . (The models can be either provided by the server or owned by the clients themselves.)
Step 2, training binary models. The server sends Ddist to all the clients. Each client duplicates its trained client model (including model weights) and swaps the model’s final classification layer with a binary classification layer (with sigmoid activation to ensure the output is [0,1]). We call these new models binary models (Mb1 ⋯ MbN ). Then the binary models are trained with both Ddist and Di (i = 1 ⋯ N ), while Ddist will have labels of 0s, and Di will have labels of 1s.
Step 3, training the server model. The clients run their models (both Mi and Mbi ) with Ddist and send the outputs to the server (where the output of Mi becomes soft labels, and the output of Mbi becomes aggregation weights). The server aggregates these outputs (into aggregated soft labels) and then uses these aggregated outputs and Ddist to train model M.
We can see that the data communication between the server and the clients only occurs at the beginning of each step. The model training processes can be totally off-line.
The most important part of DLAD is how to design the confidence of each model towards a certain sample, as well as the aggregation method. In our implementation, we define the confidence of client i towards sample x as Ci (x ) = Mbi (x ). The concept of designing Ci (x ) is that Ci (x ) should become larger if the model Mbi recognizes sample x similar to its own data Di and becomes smaller otherwise.
Then, we aggregate Ci (x ) from all the clients, to calculate a confidence weight for each client, which is

wi (x ) needs to be normalized across all the clients to ensure that it has the same scale. The above equation is equivalent to a softmax normalization, with a hyper-parameter T that adjusts the smoothness of output. Then the final aggregation result which is also the label to train the model M would be

There are also some limitations of the design of DLAD. First, it requires each client to additionally train a model of Mbi . Second, it is not always true that the more overlapping between Ddist and Di , the higher Mbi (x ) is, also, since the structure of Mbi is inherited from Mi , it can be biased according to the difference of model architectures. Anyway, to improve this idea, for example, we may properly define a distance function to represent the distance between any new sample x and the dataset Di , and then aggregate using Eq. 1. There are many possibilities to define this distance function. However, this exploration is not included in the current study.
3. Experiments
3.1 Problem setting
To evaluate our method, we use image classification as our task. This is a very common task of computer vision problems. In our study, we choose three datasets, namely MNIST, CIFAR-10, and CINIC-10 for evaluation. MNIST is a handwritten digit database, which includes 28×28 pixel grayscale images of single digits from 0 to 9. CIFAR-10 and CINIC-10 are both real-world photo databases, and both include 32×32 color images of 10 classes. All of them are commonly used and publicly available.
Note that image classification is a very popular problem in machine learning studies. The abundance of public datasets and baselines also attracts researchers to evaluate their machine learning models on it. However, our proposed method can be applied to any classification problem but not limited to computer vision. We hope the readers can have their own idea that how to apply this method to the real-world problems that they are facing.
In order to simulate a decentralized learning environment, we divided the datasets into client-side data and server-side data. Among them, the client-side data is paired with ground truth labels, and the server-side data is unlabeled. As in the real world, unlabeled data is always much easier to get, we assign a larger part of data to server side. Specifically, for MNIST and CIFAR-10, among their training sets (60,000 and 50,000 samples, respectively) we assign 80% samples to server side and 20% samples to client side. For CINIC-10, the whole validation set (90,000 samples) is assigned to server side, and the whole training set (90,000 samples) is assigned to client side.
After that, for each client, its own data Di is created by repeatedly and randomly sampling (allowing duplicates) from the data assigned to client side, until Di reaches a predetermined number of data samples (which is arbitrarily determined as 6,000 for MNIST, 5,000 for CIFAR-10, and 20,000 for CINIC-10). If the data distribution is IID, Di will include data of all ten classes. If the data distribution is non-IID, Di will only include data of a part of classes. For simplicity, Di is a balanced dataset. For example, if Di includes data of six classes, the probability of each class being sampled should be 1/6. In a real-world problem, Di might be unbalanced, but it should not affect the performance of DLAD.
In order to simulate the different levels of non-IIDness existed in the real world, we defined one type of IID and three types of non-IID data distributions. They are shown in Table 1. As either MNIST, CIFAR-10, or CINIC-10 has 10 classes of data (noted as c0~c9 in Table 1), for simplicity, when we define the data distribution, we assume that the number of clients is a multiple of five (client 1~5 have the same data distribution as client 6~10, and so on).
- IID: all ten classes are accessible to all clients.
- Non-IID #1: every two classes are exclusively accessible to only one client, e.g., c0 and c1 are accessible to client 1; c2 and c3 are accessible to client 2; and so on.
- Non-IID #2: c0~c4 are accessible to all clients, and c5, c6, c7, c8, c9 are exclusively accessible to only one client each.
- Non-IID #3: every class is accessible to only two clients among five, e.g., c0 is accessible to clients 1 and 2; c1 is accessible to clients 1 and 3; and so on.
| Client Index | 5n+1 | 5n+2 | 5n+3 | 5n+4 | 5n+5 |
|---|---|---|---|---|---|
| IID | c0~c9 | c0~c9 | c0~c9 | c0~c9 | c0~c9 |
| Non-IID #1 | c0, c1 | c2, c3 | c4, c5 | c6, c7 | c8, c9 |
| Non-IID #2 | c0~c4, c5 | c0~c4, c6 | c0~c4, c7 | c0~c4, c8 | c0~c4, c9 |
| Non-IID #3 | c0, c1, c2, c3 | c0, c4, c5, c6 | c1, c4, c7, c8 | c2, c5, c7, c9 | c3, c6, c8, c9 |
3.2 Experiment setting
The experiment involves all the three steps of the training process that were mentioned in Section 2.4.
Step 1, training client models. Theoretically speaking, it is possible to assign any type of supervised machine learning model to each client, e.g., support vector machine, decision tree, and so on. In our experiment, though, we tested two deep learning models: ResNet18 8) and DenseNet 9). The reason for adopting them is that both models are typical deep learning models that are usually seen in papers. We use pre-trained weights (on ImageNet) on both ResNet and DenseNet to reduce the necessary training time. Each client model Mi is trained for 50 epochs with a batch size of 250. Adam optimizer with the learning rate of 0.001 is applied (the same below).
Step 2, training binary models. After client models are trained, we duplicate each client model and swap the final layer with a binary-output layer to get the binary model Mbi and train them for 20 epochs. If the training sample is from Di, we additionally apply a sample weight of 1.5 to alleviate the effect of data imbalance since in our problem setting Di has much fewer samples than Ddist (see Section 3.1).
Step 3, training the server model. The server model is also chosen from ResNet and DenseNet, and its initial weights are also pre-trained weights on ImageNet. It is trained for 100 epochs. A temperature parameter T of 0.05 is used for calculating the weight aggregation as in Eq. 1.
During all the three training steps, data augmentation is applied to the input data to increase the robustness, where the following operations are used: rotation (within±20º), shift in width, height, and color (within 20%), and horizontal flip.
We compare the result of standard DLAD with the other two baselines. One is simple averaging, where the aggregation weight wi (x ) is fixed as 1/N (N is the number of clients). The other is labeled confidence, which calculates aggregation weight in the same manner as DLAD, but instead of letting the confidence Ci (x ) = Mbi (x ), it uses a ground truth label to express Ci (x ). This ground truth label is equal to the class distribution probability. For example, for the four distribution cases (IID and non-IID #1~3) in Table 1, if sample x belongs to c1, Ci (x ) is equal to 1/10, 1/2, 1/6, and 1/4, respectively, when i = 1, and equal to 1/10, 0, 1/6, and 0, respectively, when i = 2. The former baseline is the traditional strategy used in most (even recently) decentralized learning frameworks10,11), while the latter one can be treated as DLAD with ideal values of confidence, which is also a theoretical upper bond of DLAD.
3.3 Experiment results
To evaluate the performance of our proposed method in various situations, we conducted three experiments. Their details are listed in Table 2. We control the variables of dataset, distribution, client model architecture, global model architecture, and the number of clients. The experimental results are discussed as follows.
| Variable | Dataset | Distribution | Client model | Global model | No. of clients |
|---|---|---|---|---|---|
| Exp1 | MNIST, CIFAR-10, CINIC-10 | IID, NIID 1~3 | ResNet | ResNet | 10 |
| Exp2 | CIFAR-10 | NIID 1 | ResNet, DensNet, both | ResNet, DenseNet | 10 |
| Exp3 | CIFAR-10 | NIID 1~3 | ResNet, DensNet, both | ResNet | 5, 10, 20, 30 |
Due to space limitations, we do not quote the complete results of experiments 1~3 in this article (they are described in the original paper). We will use Fig. 3 as an example (experiment 1 on CINIC-10) to show how the experiment results look like. In Fig. 3, the first 50 epoch is Step 1 which represents the training process of 10 client models, and the last 100 epoch is Step 3 which represents the training (knowledge distillation) process of the server model (noted as “global” in the figure). Step 2 is unrelated to the image classification task, so it is not shown. In Step 1, the black line represents the mean validation accuracy while the gray shade represents the area between max and min accuracy of all client models. In Step 3, the red line is the accuracy of standard DLAD; the green line is the method of simple-average aggregation; the blue line is DLAD with labeled confidence (they were explained in Section 3.2).
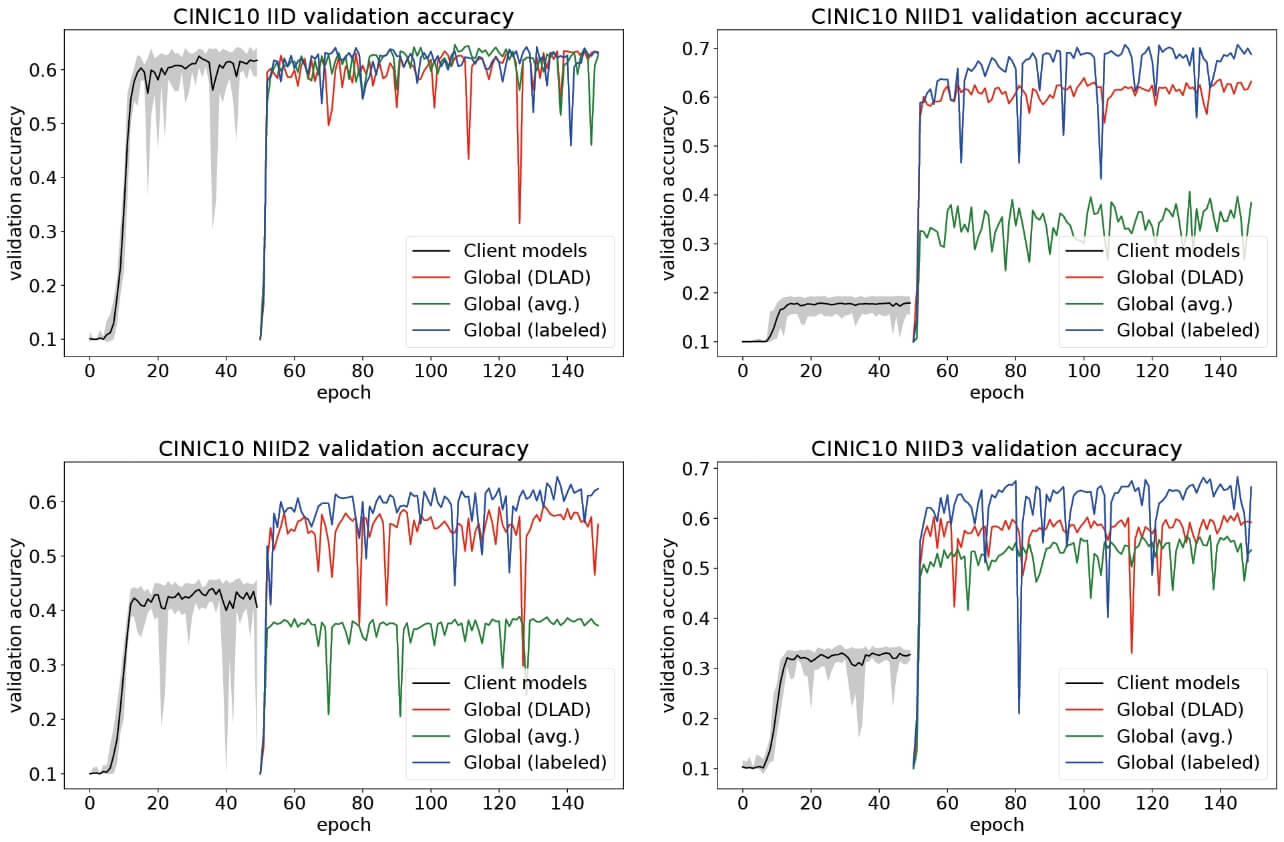
From Fig. 3, we can find the following facts:
- For the IID case, since there is no difference in data distribution and model architecture among clients and server, the server model is unlikely to be benefited or disturbed by any decentralized learning method. Still, the sever model converges faster compared with client modes, and its final accuracy is a litter higher, which is probably due to the effect of soft labels and a larger number of training samples.
- For the three types of non-IID cases, client models’ accuracies are obviously low because they only have access to two, six, and four classes of training samples, respectively (in other words, their performance would be capped at 0.2, 0.6, and 0.4, respectively). In this situation, simple-average aggregation (green) played a limited role where it helped boost accuracies in non-IID #1 and #3 but lost accuracy in non-IID #2. In other words, simple average is not suitable for all the non-IID cases. Compared to that, DLAD (red) showed its effectiveness as well as stableness in all the three non-IID cases. With labeled confidence (blue), the performance can be further improved.
The above results have already shown the usefulness of our proposed DLAD method compared to the commonly used simple-average aggregation. From our other experiment results described in the original paper but not shown here, we have other observations as follows.
- About datasets: The difficulty of tasks is like MNIST < CIFAR-10 < CINIC-10, so their accuracies decrease accordingly. Anyway, DLAD showed no abnormal behavior on all three datasets.
- About model architectures: In about half experiments, using a combination of ResNet and DenseNet as client models gave better results in server model performance, compared with using identical architecture (ResNet or DenseNet only). Our experiments only tested two model architectures, so it might be not enough to prove that diversity in client model architectures necessarily benefits DLAD results. But still, allowing customization of client models without harming the overall performance will be a great plus for real-world problems.
- About the number of clients: The performance of DLAD showed a generally increasing trend with the number of clients. It indicates that DLAD is potentialized for large-scale usage.
To recap, the effectiveness of DLAD mainly attributes to the mechanism of aggregation weights. If we can precisely estimate the confidence of client models when doing aggregation, the performance of DLAD will be enhanced to approach a high level (as DLAD with confidence labels). On the other hand, if we cannot estimate the confidence due to some reasons, the performance of DLAD will be downgraded to approach the simple-average method. One of the possible reasons is the domain difference between Di and Ddist . For example, assume Di is the data of Asian patients and Ddist is the data of American patients, then a binary classifier can easily distinguish between the two groups no matter their samples have the same label or not. We should prevent such a case because no client model will show predominant confidence and thus the aggregation weights will not work as intended.
4. Conclusion
Starting from the background of decentralized learning, this article introduced the details of DLAD, which is an original decentralized learning approach based on knowledge distillation. The article mainly answered the following questions:
- Why is decentralized learning useful?
- What are the features of federated learning and knowledge distillation?
- How does our method solve the non-IID issue?
- How is our method implemented?
- How do the experimental results of our method compare with baselines?
The author believes that decentralized learning, either FL-based or KD-based, is a very promising and applicable technology for practical use. Hopefully, this article can stimulate readers’ interest and bring fresh ideas even new business chances to their domains.
References
- 1)
- J. Ma, R. Yonetani, and Z. Iqbal, “Adaptive distillation for decentralized learning from heterogeneous clients,” in 2020 25th Int. Conf. Pattern Recognit. (ICPR), 2021, pp.7486-7492.
- 2)
- A. Hard et al., “Federated learning for mobile keyboard prediction,” arXiv. preprint arXiv:1811.03604, 2018.
- 3)
- H. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas. “Communication-efficient learning of deep networks from decentralized data,” in Proc. 20th Int. Conf. Artificial Intelligence and Statistics, 2017, pp.1273-1282.
- 4)
- K. Bonawitz et al., “Towards federated learning at scale: System design,” arXiv. preprint arXiv:1902.01046, 2019.
- 5)
- T. Nishio and R. Yonetani, “Client selection for federated learning with heterogeneous resources in mobile edge,” in ICC 2019 - 2019 IEEE Int. Conf. Commun., 2019, pp.1-7.
- 6)
- J. Konečný et al., “Federated learning: Strategies for improving communication efficiency,” arXiv. preprint arXiv:1610.05492, 2016.
- 7)
- G. Hinton, O. Vinyals, and J. Dean, “Distilling the knowledge in a neural network,” arXiv. preprint arXiv:1503.02531, 2015.
- 8)
- K. He, X. Zhang, S. Ren, J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., 2016, pp.770-778.
- 9)
- G. Huang, Z. Liu, L. van der Maaten, and K. Q. Weinberger,“Densely connected convolutional networks,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., 2017, pp.4700-4708.
- 10)
- J. H. Ahn, O. Simeone, and J. Kang, “Wireless federated distillation for distributed edge learning with heterogeneous data,” in 2019 IEEE 30th Annu. Int. Symp. Personal, Indoor and Mobile Radio Commun. (PIMRC), 2019, pp.1-6.
- 11)
- D. Li, and J. Wang, “Fedmd: Heterogenous federated learning via model distillation,” arXiv. preprint arXiv:1910.03581, 2019.
The names of products in the text may be trademarks of each company.














