3次元画像計測におけるステレオマッチングの基礎から最先端まで
ステレオマッチングは、自動運転における環境認識や自律走行ロボットのSLAM、Augmented Reality (AR)、3次元スキャンなど、さまざまな分野において基盤的技術要素となっている3次元画像計測技術の一つである。コンピュータビジョン分野の歴史の中で、最も古くから取り組まれている問題の一つでもあるが、物理的拘束や幾何学的拘束に基づいて技術構築してきたこの古典的領域に、いま、AI(深層学習技術)が侵食し、新たな展望が見え始めた。本論では、ステレオマッチングの基本的な問題設定や課題、深層学習以前のアプローチ、そして深層学習以降の最新の研究動向を解説し、さらにオプティカルフローやマルチビューステレオなどの周辺分野の紹介も交えながら、この分野を包括的に俯瞰する。
1. まえがき
ステレオマッチングとは、同一の静止シーンを別視点からとらえた2枚の画像を用いて、画像中に写るシーンの奥行きを推定する問題であり、人間の両眼奥行き知覚を計算的に模倣した3次元画像計測技術の一つである。ステレオマッチングは、コンピュータビジョン分野において最も古くから取り組まれている問題の一つであり、同時に、現在でも国際会議などで盛んに研究が発表されている問題でもある。ステレオマッチング技術の応用は幅広く、自動運転における環境認識や自律走行ロボットのSLAM、Augmented Reality (AR)、3次元スキャンなど、さまざまな分野における基盤的技術要素となっている一方、コンピュータビジョン分野内で見ても、オプティカルフォローやマルチビューステレオなどの他の問題に対する基礎的な問題と位置づけることができる。近年の深層学習の台頭は、コンピュータビジョン分野に大きな転換期をもたらしたが、ステレオマッチング分野もその例に漏れることなく深層学習の影響を強く受けた。本論では、ステレオマッチングの基本的な問題設定や課題、深層学習以前のアプローチ、そして深層学習以降の最新の研究動向を解説し、さらにステレオマッチングの周辺分野の解説も交えながら、この分野を俯瞰する。本論は、池内克史編纂のComputer Vision: A Reference Guideへ筆者が寄稿した“Binocular Stereo”の章1)の内容に対して、和訳および最新動向等を踏まえた加筆・修正をしたものである。
2. ステレオマッチングの基礎
2.1 基本知識
ステレオマッチングにおける基本的な想定として、対象は静止シーン、つまり2枚の画像間で被写体が動いていないシーンとし、さらに2枚の画像の内容は互いに十分な視覚的重なりがあるとする。
ステレオマッチングの撮影システムは、通常は、向きが揃えられた2台の同種のカメラを水平方向に並べて設置する。この際のカメラ間の距離を“ベースライン長”と呼ぶ。このとき、ステレオマッチング問題は、一方の視点画像の各画素について、それに対応する被写体上の点がもう一方の視点画像のどの位置に写っているかを推定する問題、即ち、画像間の密対応点推定問題(dense correspondence estimation)に帰着する。特にステレオマッチングの対応点ペアは、画像上で同一の高さの水平スキャンライン上に存在するため、2点間の対応関係を通常は水平方向の座標の変位、すなわち視差(disparity)によって表す。したがって、ステレオマッチングは、2枚の画像間での視差を各画素について求める問題とも言える。
ステレオマッチングによって得られる出力の形式として、奥行きマップ(depth map)や視差マップ(disparity map)などがある。奥行きマップは、メートルなどを単位とした各画素の奥行き値を画像で表したもので、視差マップは画素数を単位とした視差値を画像で表したものである。これら2つの表現は、撮影システムのベースライン長とカメラの焦点距離などの情報があれば相互に変換できる。
2.2 背景および周辺知識
人間の両眼奥行き知覚のように、ステレオマッチングも三角測量の原理を用いており、その数学的原理はエピポーラ幾何学(epipolar geometry)により基礎づけられている2)。ただし、エピポーラ幾何学自体は、基本的に、画像間の対応点を既知としてカメラや物体間の3次元的な位置関係について数学的理解を与えたり、逆に、カメラ同士の位置関係を既知として画像座標上での被写体の位置関係について数学的理解を与えたりするもので、実際にどのようにして画像中に対応点を見つけるかまではその範疇にない。これはステレオマッチング問題の要となる。
我々が普段全く意識することなく行っている両眼奥行き知覚であるが、改めて少し考えると、実に高度な処理をしていることがうかがえる。例えば、左視点のある点が右視点のどこにあるかを探すとき、その一点のみの色で判断しても対応点を一意に定めることは難しい。したがって、ある点の対応点を探すにしても、その周辺の視覚的コンテキストを見ながら、広域的な手掛かりと局所的な手掛かりを総合してマッチングしていることが推察される。これは、局所的な手掛かりのみでは残る曖昧性を、広域的な手掛かりで補っているとも言える。似たようなことはステレオマッチングでも行うが、しかし、図1の上図に示すような、全くテクスチャがない領域や繰り返しパターンが存在するシーンだと、広域的な手掛かりをもってしても対応関係に曖昧性が生じて、不良設定問題となる。これらテクスチャなし物体や繰り返しパターンの問題は、ステレオマッチングの基本的な課題に数えられる。また、鏡面反射する物体や、光沢のある物体など、視点によって見た目や明るさが変化する物体も、ステレオマッチングが原理的に難しい対象である。

このほか、二眼のステレオマッチングにおいて避けて通れない問題が、遮蔽(occlusion)である。これは、図1の下図に示すように、一方の視点画像で写っている被写体領域が、もう一方の視点画像において視界に入らない、或いは、他の被写体で遮蔽されることで画像中に写らない問題を指す。遮蔽が生じている領域では、真の意味での対応点は存在しないので、原理上、対応点/奥行き推定は失敗する。ステレオマッチング問題では、このような遮蔽領域は多かれ少なかれ必ず存在するため、基本的に遮蔽の取り扱い(occlusion handling)が必要になる。
ワイドベースライン・ステレオマッチングは、ステレオマッチングにおいて特にベースライン長が大きい場合を指す。ベースライン長の大小は対象シーンの奥行きのスケールとの相対関係で定まるが、ベースライン長を大きくとることで、奥行きを何センチ単位まで測れるかといった意味での計測の限界精度を上げられるメリットがある。一方で、デメリットとして、視差の取りうる範囲が大きくなる、画像間の視覚的重なりが少なくなる、被写体の遮蔽領域が増える、画像間での被写体の見た目の幾何学的変化が大きくなる、などが挙げられ、奥行き推定の難易度は増す。
ステレオマッチングは、一方でまた、コンピュータビジョン分野の他の問題を特殊化、或いは、簡単化したものと見なせる。
例えば、マルチビューステレオ(multiview stereo)は2視点以上からの多視点画像を用いるもので、通常はカメラの位置関係や撮像モデルは既知とする一方、カメラ配置や画像枚数は任意とする。複数の視点画像を用いることで、マッチングの曖昧性を減らせ、また、より多くの物体表面が最低2視点以上から観測できるようになるため、遮蔽問題も軽減できる。このため、原理上、マルチビューステレオは二眼のステレオマッチングよりも高い精度が期待される。一方で、不規則なカメラ配置では、例えば物体正面側と裏面側など、視覚的重なりが少ない画像ペアが存在する場合があり、これらをマッチング対象から適切に除外するための視点選択(view selection)という新たな問題をはらむ。また、不規則なカメラ配置下では、ある視点画像上でカメラと正面平行な小平面(パッチ)が、別視点では大きく歪んで写る場合があり、単純な正方形パッチ同士の類似度評価では精度を落とす。このように、マルチビューステレオは、二眼のステレオマッチングを一般化した、より複雑なタスクであると言える。
一方、オプティカルフロー(optical flow)は、ステレオマッチングと同様に2枚の画像間での対応点を推定する問題であるが、奥行きではなく、被写体の動きそのものを推定する。対象となる2枚の画像は、動的なシーンを1台の可動カメラにより異なる時刻に撮影したものである。このときフレーム間の対応点の動き(フロー/flowという)は、被写体の動きによるものや視点カメラ自身の動き(ego motion)によるもの、或いは、その両方の複合効果かもしれない。もし被写体が全く動かず、カメラモーションが正面平行な左右方向であれば、オプティカルフロー問題はステレオマッチング問題と一致する。ステレオマッチングにおける対応点の動き(視差)は、被写体の奥行き方向の位置のみを変数として説明可能だが、オプティカルフローにおける対応点の動き(フロー)は、物体の位置や動き、未知の視点モーションと、説明変数が複雑化する。このため、二眼ステレオマッチングやマルチビューステレオでは視差や奥行きといった1次元の探索空間で推定可能であったが、オプティカルフローの推定では2次元の探索空間が必要となる。遮蔽問題も依然として存在し、静的シーン下での幾何学的解釈が可能だったステレオマッチングの遮蔽問題と比べ、動的物体の存在が遮蔽の発生原理をより複雑にしている。
ステレオ・シーンフローは、二眼のステレオマッチングとオプティカルフローを組み合わせた問題で、移動可能な二眼カメラシステムにより撮影された4枚の画像(2視点×2フレーム)から、シーンの奥行きと時間方向のフローを同時に求める問題である。これらの2種類の対応点情報は、フレーム間のカメラモーション情報と併せることで、3次元空間での被写体表面の3次元的な動き(3次元シーンフロー)を表すことができる。ステレオ・シーンフローは、ステレオマッチングやオプティカルフロー単体よりも扱える情報が増えるため、複数画像からの手がかりを適切に利用すれば精度向上や高速化が見込める3)。
このように、二眼のステレオマッチング問題は、コンピュータビジョン分野に存在する様々な密対応点推定問題の中で最も根本的な問題と考えることができ、また同時に、次節以降で述べるように、カメラキャリブレーションや、画像フィルタ、組合せ最適化など、同分野の様々な技術の上に成り立っている技術でもある。
2.3 数学的原理
ここでは、エピポーラ幾何学にもとづくステレオマッチングの数学的原理を説明する。ここでの目標は、物体表面上の点の3次元座標が、どのようにしてステレオ画像間の対応点情報と紐づけられるかを数学的に理解することである。
ステレオマッチングでは一般に、図2に示すような、平行化された(rectified)設定を考える。ここでは、2台の同一のピンホールカメラが、どちらも3次元座標系のz軸方向の向きで、それぞれ原点(0, 0, 0)T と、そこから水平方向にシフトした位置(b , 0, 0)T に設置されているとする。このとき、原点の視点を左視点、もう一方を右視点と呼び、その間隔b をベースライン長とする。カメラは両方ともキャリブレーション済みとし、以下の同一の内部パラメータ行列を持つとする。
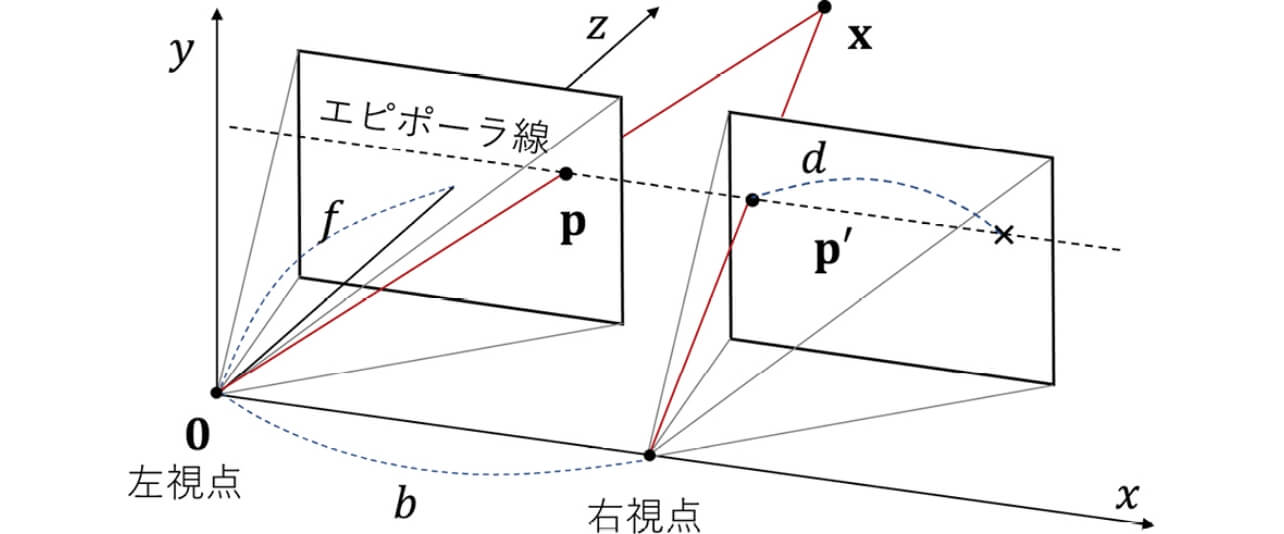
同じ向きに左右に設置されたカメラで撮影されたシーンにおいて、3次元点xが左右の視点画像に投影される状況を考える。このとき投影点の画像座標pおよびp′は、同じ高さのライン(エピポーラ線)上に位置する。カメラのベースライン長をb 、焦点距離をf とするとき、この対応点間の水平方向の座標の変位d は、3次元点の奥行きz に対応してd =fb/z と表される。
![K=[f 0 Cu 0 f CV 0 0 1]](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-008-fig-01.svg)
ここで、(cu , cv )はカメラの光学的な主点(principal point)を表し、f は焦点距離(focal length)を表す。なお、現実にはこのような理想的に平行化されたステレオ撮影システムを構築することは困難であるが、カメラシステムがキャリブレーション済み(即ち、2台のカメラの相対的姿勢と内部パラメータが既知)であれば、ステレオ画像平行化(stereo image rectification)2)と呼ばれる技術により、撮影画像をあたかも図2の平行化されたシステムで撮影したかのように変換できる。よって、以降はこの平行化されたステレオを前提に議論を進める。
原点に座する左視点を参照視点(reference view)として、この視点画像に写る物体表面上のある点に注目し、その画素の座標をp = (u , v )T とする。我々が知りたいのは、参照カメラ座標系における、この対象点の3次元座標x = (x , y , z )T であり、これはピンホールカメラの投影モデルから以下のように表せる。

ここで、

![P'=π(K[R t]x)](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-008-fig-03.svg)
ここで、[R t]は一般にカメラ間の相対的姿勢を表す、回転行列(rotation matrix)R と並進ベクトルt(translation vector)から成る3×4の姿勢行列で、今、カメラは同一方向に間隔b で設置されているため、R は3次元の単位行列、t = (-b , 0, 0)T である。姿勢行列は、xの同次座標

![P'=P-[fb/z 0]](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-008-fig-04.svg)
式(4)は、つまり、左画像上の各画素pについて、その右画像上での対応点の座標

のことを視差(disparity)と呼ぶ。式(5)からわかるように、点pの視差d 、即ち、対応点
3. 非学習型のステレオマッチング
これまでの内容により、ステレオマッチングの基本的な定義や難しさ、他の問題との関連性、そして数学的な原理について理解できたはずである。以降では、より具体的な方法論について紹介することとし、ここではまず、深層学習登場以前の非学習型の古典的アプローチについて包括的に解説する。
3.1 定式
古典的なステレオマッチング手法の俯瞰的な理解として、ScharsteinとSzeliski4)による分類が有名である。彼らはステレオマッチングのアルゴリズムを、マッチングコストの計算(matching cost computation)、コスト集約(cost aggregation)、視差計算と最適化(disparity computation and optimization)、視差微調整(disparity refinement)の4つのステップに分割することで、ステレオマッチング手法の分類を与えた。本解説では、古典的なステレオマッチング手法を、以下の式で表される目的関数の定義および最小化方法の組み合わせととらえる新たな観点を導入して俯瞰的理解を試みる。

ここで、変数







この目的関数を主眼とした観点を用いると、古典的なステレオマッチング手法は、ローカルモデル手法とグローバルモデル手法の2種類に分別できる。ローカルモデル手法は、式(6)において、マッチングコスト項のみによる目的関数

グローバルモデル手法は、正則項R (




以下では、これらローカルモデル手法およびグローバルモデル手法において重要となる要素や技術について解説する。
3.2 見た目の整合性尺度(photo-consistency measure)
マッチングコスト項の中で、おそらくもっとも重要な要素は、左右の画像での画素間の類似度(正確には非類似度)を測る尺度、即ち、photo-consistency関数



という定義を用いる場合もある。
より頑健な尺度として、2つの画像パッチに対する、以下のようなNCC(normalized cross correlation、日本語では正規化相互相関)を用いる場合もある。

ここで、





ここで、閾値τ を0 < τ < 2の範囲の値(典型的にはτ =1)に設定することで、類似度が一定値以下の場合についてNCCの値の変動を無視することができ、遮蔽領域などにおける外れ値に対して頑健な尺度を与えることができる。一方で、NCCは比較的計算コストが高いという問題がある。
ZabihとWoodfill6)は、画像パッチを2値のベクトルに変換することで、パッチ間の非類似度をハミング距離により高速に計算する手法、CENSUS変換を提案している。CENSUS変換は、あるパッチに対し、パッチ内の中央画素pとその他の画素qの輝度差の正負
3.3 コスト集約(cost aggregation)
photo-consistency関数は上述の通り、1画素、或いは、小さなパッチ単位で非類似度を評価するため、それ単体ではマッチングの曖昧性が高く、ノイズに弱い傾向がある。そこでコスト集約では、マッチングコストCp(d )を計算する際に、



ここで、Wp は対象画素pを中心とするサポート窓(support window)と呼ばれる領域であり、

コスト集約は、しばしばコストボリューム・フィルタ(cost volume filtering)とも呼ばれる。その理由を理解するために、式(10)の計算を、生のマッチングコスト値








コスト集約操作の妥当性は、サポート窓Wp内の画素sは中心画素pと同じ視差(奥行き)を持つ、という仮定に基づいている。しかし、Blayer et al.7)が議論する通り、この仮定は次の2つの場合において頻繁に破られる。1)窓内に物体の境界が存在するとき、および、2)窓領域が正面並行ではない、大きく傾いた被写体表面を写しており、視差が窓領域内で大きく変動するときである。前者は、推定された視差マップにおいて、物体境界を滑らかにするアーティファクト(boundary flattening)を生じさせ、後者は、傾いた表面に対して階段状のアーティファクト(staircase artifact)を招く。これらの問題は大きなサポート窓を使うほど顕著になる一方で、マッチングコストの信頼性をあげるためには窓サイズを大きくする必要があり、このトレードオフが大きな足かせになっていた。
1つ目の問題は、適応的なサポート窓(adaptive support-window)を用いるアプローチ8)により効果的に対処可能である。適応的サポート窓は、対象画素pとそのサポート画素sの類似度により重み付け

YoonとKweon8)による適応的サポート窓は、対象画素(aの中心点)のサポート窓(a)に対して、輝度類似度ベースの重み(b)と距離ベースの重み(c)を組み合わせたバイラテラル・フィルタカーネル(d)を計算し、マッチングコストを集約する。実際の奥行きマップ(e)と比べると、効果的に対象画素と異なる物体表面を集約計算から除外できている。
2つ目の問題の原因は、サポート窓に対して常に正面平行な面を仮定することで、視差マップ全体に正面平行バイアス(fronto-parallel bias)が生じることである。この問題に対してBleyer at al.7)は、サポート窓に対して単一の視差d を推定するのではなく、以下のように、視差を平面式d =au +bv +c で表し、各画素pに対して平面パラメータ(a , b , c )を推定した。

これは、窓領域で視差が線形に変化することを許容し、マッチングコスト計算で生じる正面平行バイアスを効果的に軽減した。一方で、視差の表現は1次元の離散値から、3次元の連続値(a , b , c )でパラメータ化された平面に代わり、この推定には後述の連続値視差推定のアプローチが必要となる。
3.4 正則化(regularization)
ローカルモデル手法では、これまでに述べたphoto-consistency関数とコスト集約を用いて、マッチングコスト関数をいかにして設計するかが中心となる。しかしながら、マッチングコスト関数だけではテクスチャが弱い領域、照明変動、画像ノイズなどの存在によって、推定精度が低下することがある。そこでグローバルモデル手法は、正則項R (


最も単純な正則化モデルは、以下のような線形モデル(linear model)である。

ここで、


このため、実用的には線形モデルに閾値τ を導入した、以下の閾値付き線形モデル(truncated linear model)が最も広く用いられる。

このモデルを用いたE (

左の線形モデル(1階平滑化モデル)には正面平行バイアスがあり階段状のアーティファクトが生じるが、右の2階平滑化モデルでは傾いた面もなめらかに推定されている。出典:Woodford et al.12)の発表資料より。
このステレオマッチングの正則化における正面平行バイアスを軽減させるために、これまでに様々な正則化モデルが提案されている。Woodford et al.12)が提案した2階平滑化モデル(second-order smoothness model)は、Dpの1回微分値

3.5 最適化(optimization)
最適化はグローバルモデル手法において必須の工程で、2変数関数、或いは多変数関数の正則項を含む目的関数E (

視差が離散変数であり、かつ、目的関数が高々2変数関数しか含まない場合、離散最適化手法(組合せ最適化手法とも呼ばれる)を直接適用して近似解を求めることが可能である。この場合の最適化方法には確立されたものがあり16)、アルファ拡張/拡張移動法(alpha expansion/expansion move)に代表されるグラフカット法(graph cuts)ベースのアプローチと、信頼度伝搬法(belief propagation)やSequential Tree Reweighted Message Passing(TRW-S)法に代表されるメッセージ伝搬法(message passing)ベースのアプローチに大別される。グラフカット法ベースの手法は、現在の視差マップの推定値に対して、画素ごとに現在ラベルと提案ラベルのどちらが良いかを選択する2値問題を反復的に解くことで、視差マップを更新していく。一方、メッセージ伝搬法は、各画素とその近傍画素の間で、ラベルに関する信頼度メッセージを交換しながら、コストボリュームを更新していく。これらの最適化アプローチは比較的高い計算量を要求するものが多く、リアルタイム・システムなどの実用場面においては、Semi-Global Matching(SGM)法17)が用いられることが多い。SGM法は、メッセージ伝搬法の近似アルゴリズムであることが知られている18)。
3.6 連続値の視差の推定
視差は本来連続値であるため、より正確な3次元シーンの表現と推定には、連続値の視差マップ
連続値の視差推定の一つのアプローチは、最適化の中で連続値の視差を求めることである。この場合、離散最適化手法を直接適用することはできないが、離散最適化手法を利用して連続値変数を最適化する、離散連続最適化アプローチが取られることが多い。例えば、セグメントベースの手法19)は、RANSAC法などを利用して事前計算したシーン中の平面を候補ラベルとして、スーパーピクセル領域に平面ラベルを割り当てる組合せ最適化問題として解く。融合ベースの手法12)は、多数の連続値表現の視差マップの解候補(proposal)を融合してより良い解を求めるもので、グラフカット法を用いた組合せ最適化問題として定式化される。融合ベースの手法では、解候補の生成方法が鍵となるが、例えば、様々な粒度のスーパーピクセルで推定したセグメントベース手法の結果などが用いられる(図5)。

上:参照画像に対し、様々な粒度のスーパーピクセルを推定。下:それぞれについてセグメントベース手法により視差マップ候補を生成する。視差マップ候補はグラフカットベースの最適化により融合される。出典:Woodford et al.12)より。
PatchMatchステレオ法7)は、PatchMatchと呼ばれる空間伝搬とランダム探索を組み合わせた対応点推定アルゴリズム20)を用いることで、各画素に対して連続値3次元ベクトルで表される視差平面を推定した。この手法は融合移動法と比べ、解候補の事前生成が不要である一方、正則化を考慮しないローカルモデル手法であった。PatchMatchのようなランダム探索を正則化付きのグローバルモデル手法として実現する研究として、Besse et al.21)による信頼度伝搬法ベースの手法や、筆者(Taniai et al.22))によるグラフカット法ベースの手法がある。
連続値の視差推定のもう一つのアプローチは、離散的な視差マップを推定した後にそれを後処理として精細化するものである。通常は、整数値の視差を精細化するため、そのような処理のことをしばしばサブピクセル精細化(subpixel refinement)と呼ぶ。具体的な方法として、メッセージ伝搬法によって得られる各画素の各候補ラベルに対する信頼度の値を用いて曲面フィッティングをする方法17)や、勾配法23)により目的関数E (
3.7 遮蔽対処(occlusion handling)
遮蔽問題は、推定済みの視差マップに対して後処理として対処するアプローチ7,17)と、目的関数E (
4. 学習型のステレオマッチング
深層学習の台頭により、学習型のステレオマッチング手法が近年盛んに研究されている。とりわけ、ニューラルネットワークを用いて一貫学習するアプローチが主流で、これは以下のようなステレオ画像ペアから視差マップへのマッピング関数f を直接学習する。

関数f は畳み込みニューラルネットワーク(以下CNN)により実装され、そのパラメータ





このような学習型手法の利点として、これまで非学習型の古典手法においては、マッチングコスト計算における画像パッチの歪みや照明変動の問題、遮蔽問題、ステレオ平行化やキャリブレーションの誤差などの様々な問題に対して個別に対処が必要だったが、学習型のデータ駆動アプローチではこれらがほぼ自動的に解決できる。また、CNNの推論計算はGPU上で大規模に並列化することが可能で、従来の古典手法では計算に時間がかかった連続値視差の推定も、高速に実行することができる。
既存の学習型手法を俯瞰的に理解するならば、これらはコストボリュームにもとづく古典ステレオ手法の模倣とみることができる。そこで本論では、ScharsteinとSzeliski4)による古典ステレオ手法の分類に倣い、学習型手法のニューラルネットワークの構成を、特徴抽出(feature extraction)、ボリューム構築(volume construction)、コストボリューム学習(cost volume learning)、視差回帰と精細化(disparity regression and refinement)の4つの工程に分解した。図6は、このようなニューラルネットワークの典型的な例を図示したものである。以下では、学習型手法に関する既存研究の解説も交えながら、この4つの工程の内容を解説する。

学習型のステレオマッチングでは、通常、各入力画像を特徴マップに変換した後、右特徴マップを左特徴マップ上で横断させながら連結または相関計算することでコスト特徴ボリュームを構築する。コスト特徴ボリュームは、3次元畳み込みネットワーク等によりコストボリュームに変換された後、soft-argmin演算により視差マップが出力される。
4.1 特徴抽出(feature extraction)
初期の学習型手法は、ニューラルネットワークをマッチングコストの計算に特化して用いるものだった。ZbontarとLeCun26)によるMC-CNNは、画像パッチから特徴ベクトルを抽出し、特徴ベクトル間のマッチングコストをコサイン距離(fast構成)や全結合層(accurate構成)によって計算した。学習されたマッチングコスト関数は古典手法におけるphoto-consistency関数
この特徴抽出は、後に、ステレオ一貫学習のアプローチ27-31)における種々の工程の最初のステージとしてネットワークに組み込まれた。一貫学習アプローチにおける特徴抽出の役割は、各入力画像を特徴マップに変換することであり、フィードフォワード型CNN27)やResNet型CNN28)の他、マルチスケール情報を効果的に利用する取り組みとして空間ピラミッド・プーリング(以下SSP)層29)やU-Net型CNN31)を用いた実装がある(表1参照)。
| 手法 | 特徴抽出 | ボリューム構築 | コストボリューム学習 | 視差マップの回帰出力 | |||
|---|---|---|---|---|---|---|---|
| タイプ | 特徴次元 | 方式 | 解像度 | 特徴次元 | |||
| DispNet27) | CNN | 128 | 相関 | 1/4 | 1 | なし | 2D CNN |
| GC-Net28) | ResNet | 32 | 連結 | 1/2 | 64 | 3D U-Net | soft-argmin |
| PSMNet29) | ResNet + SPP | 32 | 連結 | 1/4 | 64 | 3D U-Net×3 | soft-argmin |
| GwcNet30) | ResNet | 320 | 相関+連結 | 1/4 | 64 | 3D U-Net×3 | soft-argmin |
| GA-Net31) | U-Net | 32 | 連結 | 1/3 | 64 | SGA×3 + LGA | soft-argmin |
4.2 ボリューム構築(volume construction)
学習型ステレオは、マッチングコスト関数の学習に特化したアプローチから直接視差マップの推定まで行う一貫学習アプローチへシフトしていった。その基本的な方針は、古典手法で用いられた3次元コストボリュームをネットワーク内で計算し、そこから視差マップを回帰出力するというものである。
このアプローチに代表される初期の事例がMayer et al.27)によるDispNetCorr(以下DispNet)である。DispNetのコストボリューム構築は、左視点の特徴マップ上で右視点の特徴マップを横断させながら、特徴ベクトル間の相関を計算するもので、以下のように計算される。

これは相関ベース(correlation-based)のボリューム生成と呼ばれ、強い帰納バイアスの恩恵を受けられる一方、ボリュームの各点をスカラー表現に落とし込むため、視覚的なコンテキスト情報などが欠落する問題がある。そこで、相関を明示的に計算せずに特徴ベクトルの連結で表現する、次式のような連結ベース(concatenation-based)の拡張28)も提案されている。

さらにGuo et al.30)は、相関計算を多チャンネル化したグループ毎相関(group-wise correlation)と、連結ベースのボリューム生成を組み合わせ、相関計算の帰納バイアスと特徴ベクトルに含まれるコンテキスト情報の両方を利用する手法を提案している。
連結ベースやグループ毎相関ベースによって生成されるボリュームは、各マッチングコスト値を多次元の特徴ベクトルで抽象的に表したコスト特徴ボリュームと見なせ、4次元テンソルで表現される。このコスト特徴ボリュームはメモリ消費が多いため、通常は特徴抽出時においてW/2×H/2やW/4×H/4のサイズにダウンサンプリングされた特徴マップを用いてボリューム構築する(表1参照)。画像サイズを各辺1/s に縮小すると、視差範囲も1/s になるため、特徴ボリューム全体のメモリサイズは(1/s )3になる。生成された特徴ボリュームは、次のステップにより、明示的にマッチングコストを表す3次元テンソル表現のコストボリュームに変換される。
4.3 コストボリューム学習(cost volume learning)
古典手法では、コストボリュームに対してコスト集約やSGMなどの最適化処理を施すことで、生のマッチングコストに対して正則化を適用し、推定精度を向上させた。学習型手法でも同様の効果をねらった方法が提案されている。
DispNet27)とならんで初期の一貫学習アプローチの代表例であるKendall et al.28)によるGC-Netは、連結ベースのコスト特徴ボリューム(4次元テンソル)に対して、3次元畳み込み層によるU-Net型の3次元CNNを適用することで正則化効果を学習する。Chang et al.29)はこの3次元U-Netをカスケード化させた構成を提案した。また、Zhang et al.31)のGA-Netは、SGM最適化処理を模倣したSGM層と、適応的なサポート窓によるコスト集約を模倣したLocal Guided Aggregation(LGA)層を提案した。SGMの最適化処理は、元々微分可能な演算の組み合わせであったが、GA-Netでは、max関数をsoftmax重みとの内積に置き換えるなど、勾配を効果的に伝搬する工夫がされている。
4.4 視差回帰と精細化(disparity regression and refinement)
視差回帰は、コストボリュームから連続値の視差マップを出力する工程である。初期の学習型手法の例では、古典手法における離散視差推定のように分類ベースで行われたり、或いは、DispNet27)では、3次元のコストボリュームを2次元の特徴マップとして2次元CNNにより出力したりする方法がとられた。
これに対し、Kendall et al.28)が提案したsoft-argmin演算は、コストボリュームから効果的に連続値の視差マップを出力することを可能とし、以後の手法に標準的に用いられるようになった。soft-argminは、3次元コストボリューム

を計算し、これにより視差の期待値

を求めるものである。
このように出力された視差マップは、最終的に損失
4.5 データセット
学習型ステレオマッチングにおいては、学習データとなるデータセットや性能評価用のベンチマークの存在が重要になる。学習型ステレオマッチングの紹介の締めくくりとして、以下では、論文等において頻繁に用いられる代表的なデータセットを紹介する。
SceneFlowデータセット
Mayer et al.27)は、ステレオマッチング、オプティカルフロー、およびステレオ・シーンフロー用の大規模なCGによるデータセットを構築した。このデータセットは、学習用データとして3万5,454組、テスト用データとして4,370組のステレオ画像ペアを提供する。各画像は、960×540(0.5メガピクセル)のサイズで、正解となる視差マップのほか、前後のフレーム間のフローマップなども与えられている。Mayer et al.によるDispNet27)以降の学習型ステレオマッチング手法は、このデータセットを用いて事前学習するのが一般的となっている。
KITTI 2012・2015ベンチマーク
KITTI 2012ベンチマークは、実際の車載カメラ画像を用いて、学習用およびテスト用に対してそれぞれ200組のステレオ画像ペアを提供している。各画像は、376×1242(0.5メガピクセル)のサイズで、学習用画像中の道路や壁や標識などの背景領域についてはLiDARセンサーによって計測された正解視差が与えられる。KITTI 2015も同様の内容であるが、背景領域のみならず、車の領域に対しても3D CADモデルをフィッティングして推定した正解視差が与えられている。既存の論文では、SceneFlowデータセットで事前学習したモデルでablation studyなどの評価実験を行い、KITTIデータセットで追加学習したモデルで実画像シーンに対する評価実験を行う場合が多い。
Middlebury Stereo(バージョン3)ベンチマーク
Middleburyベンチマークは、2002年の初期バージョン4)から始まる、比較的古くからあるステレオのベンチマークで、実際の屋内シーン画像に対し、structured light技術で3次元計測した高精度な正解視差マップを提供している。現在のバージョン3では、学習用として23シーン、テスト用として15シーンあり、他のデータセットと比べシーン数は少ない。もう一つの実画像によるベンチマークであるKITTIと比べ、学習データが少ない点、大きな照明変動やテクスチャなし領域があるシーンを含む点、高解像度で視差の探索範囲が大きい点などの難しさがあり、リーダーボードでは、完全な学習型手法よりも、学習型マッチングコストと古典手法を組み合わせた手法22)が依然として強い傾向がある。
5. 他の問題への広がり
これまでに紹介した学習型のステレオマッチングのアプローチは、拡張される形で、オプティカルフローやマルチビューステレオなどの他の類似問題にも利用されている。以下では、そのような周辺分野への広がりについて簡単に紹介する。
5.1 オプティカルフロー(optical flow)
ステレオマッチングとオプティカルフローとの決定的な違いは、探索範囲の広さである。ステレオマッチングは、各画素について一定の深さまでの視差の探索範囲を定め、これをカバーするようなコストボリュームを構築する、いわば全探索アプローチがとられた。これは、ネットワーク上ではコスト特徴ボリューム(4次元テンソル)に対する3次元CNN等により実装される。しかし、オプティカルフローでは探索空間が2次元に広がるため、同様の全探索をするには、5次元テンソルに対する4次元CNNが必要となり、メモリおよび計算コストが大幅に増大する。特に学習型手法では、誤差逆伝搬のために中間層の特徴マップや特徴ボリュームの内容を全て保持しながら計算しなければならないため、メモリ上の制約が厳しい。
似たような問題は古典手法においても存在した。そこで、解決の糸口として古典手法のアプローチを振り返ってみる。古典手法の初期の代表例であるLucas-Kanade法23,33)は、ステレオのような離散最適化アプローチではなく、勾配法に基づく連続最適化アプローチであった。その登場の背景には、当時のコンピュータの性能では、大量の計算とメモリを必要とするコストボリューム生成型の離散最適化アプローチが困難であった点も一因に考えられる。勾配法ベースの手法は、フローの初期値が正解値から大きく離れていると悪い局所解に陥りやすい。このためLucas-Kanade法では、画像ピラミッドの低解像度画像からフロー推定を行い、その結果をより高解像度の画像におけるフロー推定の初期値にしながら、順々に高解像度へと結果を伝搬、更新していく、いわゆるcoarse-to-fine推定のアプローチがとられた。その後、コストボリュームの一部を効率的にサンプリングして離散最適化するアプローチとして、融合ベースの手法と勾配法による精細化の組み合わせ34)やPatchMatch法20)などが現れ、近年では、最適化処理に高速化の工夫を凝らしたフル・コストボリュームによる全探索アプローチ35,36)が登場するに至っている。
一貫学習アプローチの初期の代表例であるFlowNet37)は、コストボリューム学習を提案した先駆的手法*4であったが、メモリ制約のため極度にダウンサンプリングしたコストボリュームを使用しており、精度は古典手法にも劣った。その後、解像度と使用メモリのトレードオフを改善するアプローチとして、フル・コストボリュームを用いないLucas-Kanade法を模倣した手法が多く登場した。例えばPWC-Net38)は、低中高の3つの解像度を持つ画像ピラミッドに対して、各解像度に対応したフロー推定ネットワークを用意し、低・中・高解像度と順々にフロー推定しながら結果を次のレベルでの初期値として伝搬していく。
中でも特筆すべきは、ECCV 2020でBest Paperに選ばれたTeedとDeng39)によるRAFT(Recurrent All-pairs Field Transforms)と呼ばれる手法だ。RAFTは、



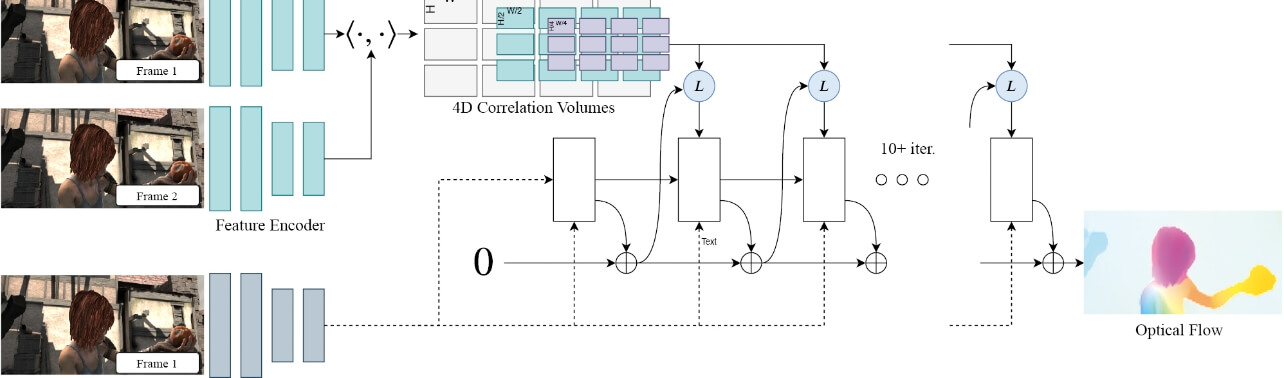
各画像を特徴マップにエンコードして4次元コストボリュームを構成した後、反復プロセスでは、現在の推定対応点周辺で4次元ボリュームを参照(“L” ook Up)しながら、GRUが組み込まれた再帰レイヤーでフローの更新量の推定を繰り返す。出典:TeedとDeng39)より。
ネットワークg の内部では、各画素について現在の推定対応点に基づいてマッチングコストをサンプリングする工程(図7のブロック“L”)と、マッチングコストと参照画像の特徴マップを入力として更新量を推定する工程(図7のブロック“□”)がある。サンプリング工程では、単に現在の推定対応点のマッチングコストを計算するのではなく、その近傍を含めた複数のマッチングコストを、マルチスケール化された複数のコストボリュームからサンプリングする。このように広域的な情報を集めることで、高解像度画像が持つ大きなフローに対しても効果的に推定できる。また、更新量推定の工程では、GRUベースの再帰レイヤーを用いている。これは、精細化用ネットワークなどの導入を不要にし、全ての反復工程を同一のネットワークで実行可能にする工夫と考えられる。
RAFTは従来のモデルと比べ、パラメータ数、推論速度、学習効率のすべての観点において、推定精度とのトレードオフを大幅に向上させた。また、CGによる人工データセットによる事前学習だけでも、実画像に対する高い汎化性能を有することを示した。同様のアプローチは、ステレオマッチングにおいても、特にメモリコストが高い高解像度画像ステレオに対して有効であると筆者は考えている。
5.2 マルチビューステレオ(multiview stereo)
ステレオマッチングは参照画像I0と目標画像I1のペアに対する対応点推定問題であるが、マルチビューステレオは、目標画像が複数枚Ii (i=1,2,...,N )に拡張された、N 組の画像ペア{I0, Ii }に対する対応点推定問題とみることができる。ただし、これらの画像は全て同一の静的シーンをとらえたもので、各視点のカメラ姿勢は既知であることを考慮すると、N 組の画像ペアに対して個別に対応点マップ(視差マップ)を推定する必要はなく、参照画像に対して1枚の奥行きマップを推定すれば、それが全ての画像ペア{I0, Ii }に対する対応点マップを表すことになる。
学習型のマルチビューステレオにおいて要となるのは、目標画像の数および視点位置が任意であるときに、それらに対する参照画像とのマッチング情報を、いかにして1枚の奥行きマップ推定の手がかりとして集約するかという点である。これをニューラルネットワークで実現するには、多少の工夫が必要となる。例えば、N 組の画像ペア{I0, Ii }について、特徴ベクトル同士のマッチングコスト




学習型手法の代表例であるMVSNet40)(図8)は、古典的アプローチにおける平面スイープ法に倣い、参照画像に対して複数の候補平面を仮定し、各平面のホモグラフィ変換により、目標画像の特徴マップを参照画像上に投影してマッチングを行う。
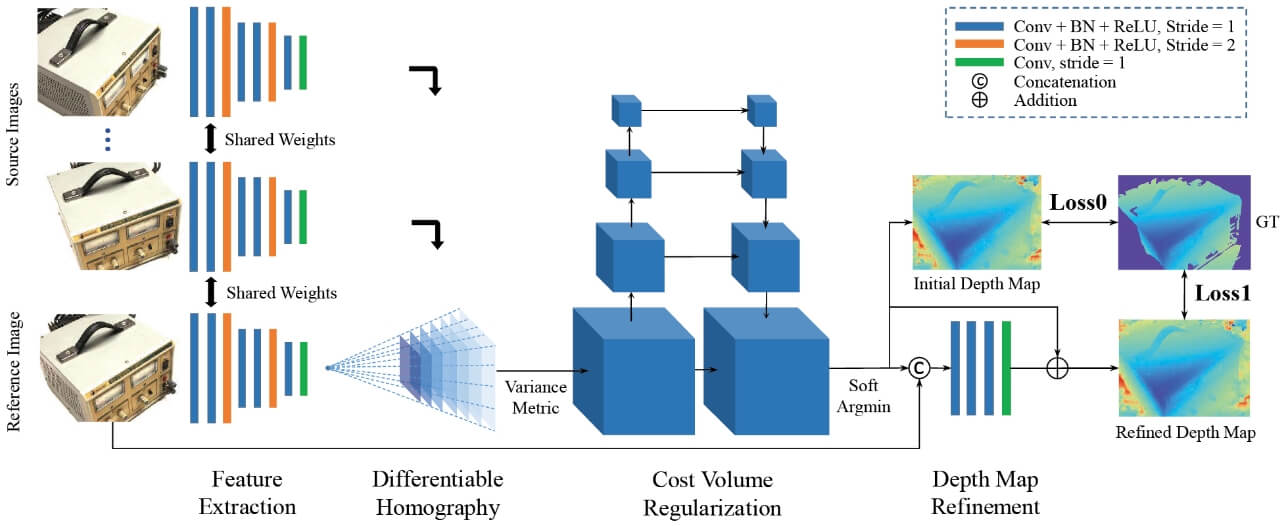
参照画像に対して複数の奥行き平面を仮定。各視点画像の特徴マップをホモグラフィ変換で参照画像上に投影し、それらを分散ベースの集約層に通すことで3次元ボリュームを生成する。出典:Yao et al.40)より。
奥行きz の候補平面によって投影された目標画像の特徴マップを


ここで、
式(17)からわかるように、MVSNetは、学習後においても目標画像の枚数N を自由に変えることができ、また、それらの画像の順番によって計算結果が変わることもない。実験では、目標画像枚数N =2で学習したモデルにおいて、推論時にN を増やすことで推定精度が向上すること、さらに、分散ベースの集約が既存の平均ベースの方法よりも優れていることなどが確認された。
8. むすび
本論では、3次元画像計測におけるステレオマッチングの基礎から最先端までと題し、ステレオマッチングの基本的な定義や課題や定式の解説に始まり、深層学習登場前後での非学習型および学習型のステレオマッチング手法のアプローチを俯瞰的に解説した。さらに、深層学習ベースのステレオマッチング手法が、オプティカルフローやマルチビューステレオといった類似問題とどのように関連しているかを、実例を交えて紹介した。本論の執筆にあたり、いかに深層学習以前の古典的アプローチにおける種々のアイディアが、その後の深層学習ベースのアプローチに直接あるいは再解釈される形で取り入られたかが分かるように書いたつもりであり、その点が読者に伝われば幸いである。
参考文献
- 1)
- Taniai, T. “Binocular Stereo”. Computer Vision. Ikeuchi, K., eds. Springer, 2020, p.83-92.
- 2)
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision. 2nd. ed. Cambridge University Press, 2003, 655p.
- 3)
- Taniai, T.; Sinha, S.; Sato, Y. “Fast multi-frame stereo scene flow with motion segmentation”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2017, p.6891-6900.
- 4)
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comp. Vis. (IJCV). 2002, Vol.47, No.1/2/3, p.7-42.
- 5)
- Móllenhoff, T.; Laude, E.; Moeller, M.; Lellmann, J.; Cremers, D. “Sublabel-accurate relaxation of nonconvex energies”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2016, p.3948-3956.
- 6)
- Zabih, R.; Woodfill, J. “Non-parametric local transforms for computing visual correspondence”. Proc. Europ. Conf. Comp. Vis. (ECCV). 1994, p.151-158.
- 7)
- Bleyer, M.; Rhemann, C.; Rother, C. “PatchMatch stereo - Stereo matching with slanted support windows”. Proc. British Mach. Vis. Conf. (BMVC). 2011, p.1-11.
- 8)
- Yoon, K.; Kweon, I. Adaptive support-weight approach for correspondence search. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2006, Vol.28, No.4, p.650-656.
- 9)
- Hosni, A.; Rhemann, C.; Bleyer, M.; Rother, C.; Gelautz, M. Fast Cost-Volume Filtering for Visual Correspondence and Beyond. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2012, Vol.35, No.2, p.504-511.
- 10)
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2012, Vol.35, No.6, p.1397-1409.
- 11)
- Ishikawa, H. Exact optimization for Markov random fields with convex priors. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2003, Vol.25, No.10, p.1333-1336.
- 12)
- Woodford, O.; Torr, P.; Reid, I.; Fitzgibbon, A. Global stereo reconstruction under second-order smoothness priors. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI). 2009, Vol.31, No.12, p.2115-2128.
- 13)
- Lempitsky, V.; Rother, C.; Blake, A. “LogCut - Efficient graph cut optimization for Markov random fields”. Proc. Int. Conf. Comp. Vis. (ICCV). 2007, p.1-8.
- 14)
- Olsson, C.; Ulen, J.; Boykov, Y. “In defense of 3d-label stereo”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2013, p.1730–1737.
- 15)
- Scharstein, D.; Taniai, T.; Sinha, S. N. “Semi-global stereo matching with surface orientation priors”. Proc. 2017 Int. Conf. 3D Vis. (3DV). 2017, p.215-224.
- 16)
- Szeliski, R.; Zabih, R.; Scharstein, D.; Veksler, O.; Kolmogorov, V.; Agarwala, A.; Tappen, M.; Rother, C. A comparative study of energy minimization methods for Markov random fields with smoothness-based priors. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI). 2008, Vol.30, No.6, 1068–1080.
- 17)
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2008, Vol.30, No.2, p.328–341.
- 18)
- Drory, A.; Haubold, C.; Avidan, S.; Hamprecht, F. A. “Semi-global matching: a principled derivation in terms of message passing”. Pattern Recognition. Springer, 2014, p.43-53.
- 19)
- Birchfield, S.; Tomasi, C. “Multiway cut for stereo and motion with slanted surfaces”. Proc. Int. Conf. Comp. Vis. (ICCV). 1999, p.489–495.
- 20)
- Barnes, C.; Shechtman, E.; Finkelstein, A.; Goldman, D. PatchMatch: a randomized correspondence algorithm for structural image editing. ACM Trans. Graph. 2009, Vol.28, No.3, Article 24.
- 21)
- Besse, F.; Rother, C.; Fitzgibbon, A. W.; Kautz, J. PMBP: PatchMatch belief propagation for correspondence field estimation. Int. J. Comp. Vis. (IJCV). 2014, Vol.110, No.1, p.2-13.
- 22)
- Taniai, T.; Matsushita, Y.; Sato, Y.; Naemura, T. Continuous 3d label stereo matching using local expansion moves. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI). 2018, Vol.40, No.11, p.2725–2739.
- 23)
- Lucas, B.; Kanade, T. “An iterative image registration technique with an application to stereo vision”. Proc. Imaging Understanding Workshop, 1981, p.121-130.
- 24)
- Kolmogorov, V.; Zabih, R. “Computing visual correspondence with occlusions using graph cuts”. Proc. Int. Conf. Comp. Vis. (ICCV). 2001, p.508-515.
- 25)
- Wei, Y.; Quan, L. “Asymmetrical occlusion handling using graph cut for multi-view stereo”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2005, p.902-909.
- 26)
- Zbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, Vol.17, p.1–32.
- 27)
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. “A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2016, p.4040-4048.
- 28)
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. “End-to-end learning of geometry and context for deep stereo regression”. Proc. Int’l Conf. Comp. Vis. (ICCV). 2017, p.66-75.
- 29)
- Chang, J.; Chen, Y. “Pyramid Stereo Matching Network”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2018, p.5410-5418.
- 30)
- Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. “Group-Wise Correlation Stereo Network”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2019, p.3268-3277.
- 31)
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P. H. “GA-Net: Guided Aggregation Net for End-To-End Stereo Matching”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2019, p.184-195.
- 32)
- Chabra, R.; Straub, J.; Sweeney, C.; Newcombe, R.; Fuchs, H. “StereoDRNet: Dilated Residual StereoNet”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2019, p.11778-11787.
- 33)
- Baker, S.; Matthews, I. Lucas-Kanade 20 Years On: A Unifying Framework. Int. J. Comp. Vis. (IJCV). 2004, Vol.56, p.221–255.
- 34)
- Lempitsky, V.; Roth, S.; Rother, C. “FusionFlow: Discrete-continuous optimization for optical flow estimation”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2008, p.8934-8943.
- 35)
- Chen, Q.; Koltun, V. “Full Flow: Optical Flow Estimation by Global Optimization over Regular Grids”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2016, p.4706-4714.
- 36)
- Xu, J.; Ranftl, R.; Koltun, V. “Accurate Optical Flow via Direct Cost Volume Processing”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2017, p.5807-5815.
- 37)
- Dosovitskiy et al. “FlowNet: Learning Optical Flow with Convolutional Networks”. Proc. Int’l Conf. Comp. Vis. (ICCV). 2015, p.2758-2766.
- 38)
- Sun, D.; Yang, X.; Liu, M.; Kautz, J. “PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume”. Proc. IEEE Conf. Comp. Vis. Pattern Recog. (CVPR). 2018, p.8934-8943.
- 39)
- Teed, Z.; Deng, J. “RAFT: Recurrent All-Pairs Field Transforms for Optical Flow”. Proc. Europ. Conf. Comp. Vis. (ECCV). 2020, p.402-419.
- 40)
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. “MVSNet: Depth Inference for Unstructured Multi-view Stereo”. Proc. Europ. Conf. Comp. Vis. (ECCV). 2018, p.785-801.
本文に掲載の商品の名称は、各社が商標としている場合があります。
- *1
- 近年では、このようなステレオマッチングのような非凸最適化問題に対して、連続最適化アプローチの限界を克服しようとする試みもある5)。
- *2
- σpや
は、実際にはゼロ除算による発散を防ぐため、小さな定数ϵを用いてmax{ϵ, σp} などとして実装される。
- *3
- Woodford et al.12)は、さらに連続値の視差を仮定した、従来よりも複雑なモデルを用いており、これらの最適化アプローチを含めた内容が評価されてCVPR 2008のBest Paper 賞を受賞している。ここで用いられた最適化法である融合移動(fusion move)法(後述)は、同グループの別論文13)として既に発表済みであったが、一連の研究を契機に融合移動ベースの最適化法がその後広く取り入れられるようになった。
- *4
- FlowNe37)はDispNet27)と同じ研究グループから発表された手法だが、実は、FlowNetのほうが先行研究であり、DispNetは後にFlowNetを応用する形で、ステレオ・シーンフローを推定するネットワークの構成要素として提案された。














