製造現場の突発的な変動の影響を受けたデータにおける異常検知の改善
- AI技術
- リアルタイム異常検知
- 品質管理
- PLC
- 機械学習アルゴリズム
人手不足の解消や、製品品質の向上は、製造現場における大きな課題であり、その改善の手段として、AI(Artificial Intelligence:人工知能)の適用が進められている。
ところが、従来のAIでは、適用が困難なケースがある。そのひとつに、AIのアルゴリズムが前提としているデータの分布と、実際の製造現場のデータの乖離がある。製造現場では、原料の変化や、治具の交換、設備の設定変更など、多くの要因に変動があり、データはその影響を受ける。このような変動があった場合、データには突発的な変動が現れる。
従来のAIは、突発的な変動がないことを前提としている。そのため、変動の影響があるデータに対して従来のAIを適用すると、誤った判定の原因となる。この改善が、AI活用の課題の一つとなっている。
本稿では、従来のアルゴリズムに、品質管理の分野で従来から使われている管理図の手法を加えた、新たなアルゴリズムを提案する。従来のアルゴリズムでは対応が困難であった現場課題について、提案手法による偽陽性率が18%であるのに対し、2種類の従来手法は、いずれも約70%であった。このアルゴリズムは偽陽性率を約50%改善でき、有効であることを確認した。
本稿により、データの変動に対応が可能なAIとして、管理図の手法による変動の検知と、逐次学習を合わせたアルゴリズムによる方向性を示す。
1. まえがき
AIの導入は、人の作業の軽減や代替を目的とするのが一般的と考えられる。例えば、オムロンにおいては、「AIを活用し、熟練検査員の技を再現」、「人と機械の新しい協調で食品製造現場の労働生産性と品質を革新」と言った表現で、AIの導入効果が説明されている1)。
AIには、様々な形態やアルゴリズムがあるが、中でも「機械学習」と呼ばれているアルゴリズムが広く用いられている2)。
機械学習では、データを用意して機械に学習させる作業がある。学習ができた機械は、予測や判定などを実行する。この機能を使って、人間が行っている予測や判定という行為を、機械で代替できるようにする。例えば、前述のような製造現場の事例においては、装置や各種センサのデータを学習データとして収集し、機械学習のモデルを構築した後、そのモデルを適用することで製造現場における異常を検知する。
従来、機械学習の適用フローとして、バッチ学習と逐次学習が知られている3)。
バッチ学習とは、ある程度の量のデータを学習用データとして用意して、それらを一括して処理することで学習する方法である。学習後は、AIを使った予測や判定の段階になる。バッチ学習では、学習用のデータを収集している間は、AIが使用できない期間になる。オムロンの商品であるAI搭載マシンオートメーションコントローラもこの方式である4)。
逐次学習とは、サンプルが増えるごとに、学習を繰り返していく方法である。逐次学習では、サンプルが増えるごとに、過去の学習用のデータに追加して、新しい学習用のデータでバッチ学習をするのではなく、過去の学習結果を、新しいサンプルで修正していく処理を繰り返して行く。これによって、大量のサンプルデータを同時に扱う必要がなくなり、計算量が少なくなる。また、学習とAIの利用時期が同時進行になり、学習用のデータを蓄積するための期間が不要になる。
このように、バッチ学習では学習のフェーズと予測のフェーズが分かれているため、データの分布の変動に追随できない。逐次学習では、データの変動に追随できるが、学習が一時的な変動の影響を受けやすい。また、過去のデータの影響があるため、分布の変化への追随は遅い。
次節で詳述するように、考え得る条件を一定にしても、このような変動は発生することがあり、機械学習を製造現場に適用する際の、課題の一つになっている。
本稿ではこのような課題の解決方法として、管理図の手法による変動の検知と、逐次学習を合わせたアルゴリズムを提案する。2章では本稿が解決する課題を示し、3章では提案手法を示す。4章は、具体的な設備による実験結果を示し、5章にて実験結果を踏まえ、提案手法を考察する。
2. 課題
データの収集を継続的に進めていると、あるタイミングで傾向が大きく変わることがある。製造現場であれば、原料の素材変化や、治具の交換、設備の設定変更など、多くの要因で起こり得る現象である。
本稿では、横ピロー式包装機における、切断時のカッターの位置のデータを用いて課題を説明する。横ピロー式包装機では、ロール状のフィルムで被包装物を囲み、熱圧着することで、被包装物が包まれた状態にする。最後に、フィルムから切断することで、包装を完成させる。切断にはカッターを用いるが、実験装置では、カッターの両端に変位センサが取り付けてあり、カッターが上下運動をして切断する時の、カッターの高さを測定している。変位センサが2つあるため、データは同時刻に2つが収集される。図1にカッターの概要図を示す。
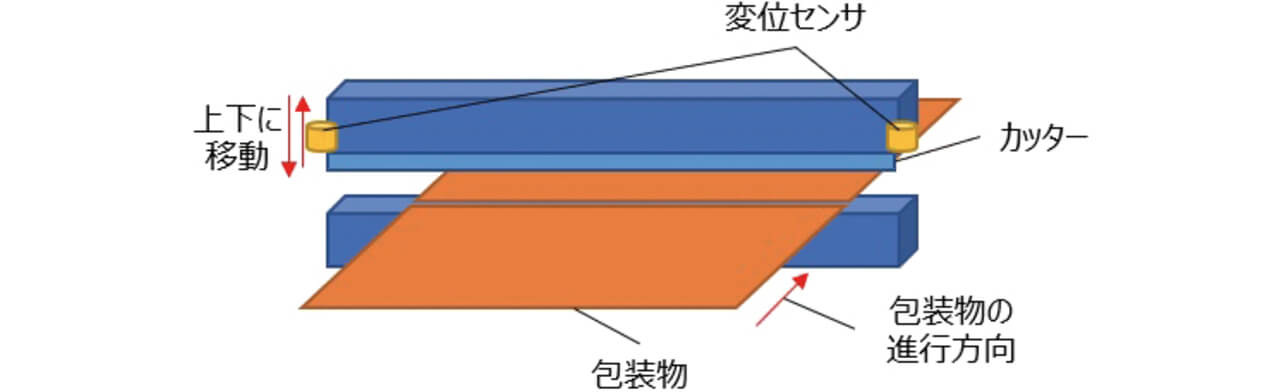
それぞれのセンサのデータを図2、図3に示す。包装後の寸法、材質、被包装物が同一の時のデータであり、途中、条件が異なるデータは除いてある。図の縦軸は、実際の変位センサのデータの測定値に対して、定数を乗じて処理したものである。ひとつのサイクルの中で、被包装物の移動や切断等の一連の動作があり、カッターの高さは変化する。その高さを変位として測定する。そのサイクルの中で、カッターが切断するタイミングの高さだけを抽出したのが、本稿で使用しているデータである。
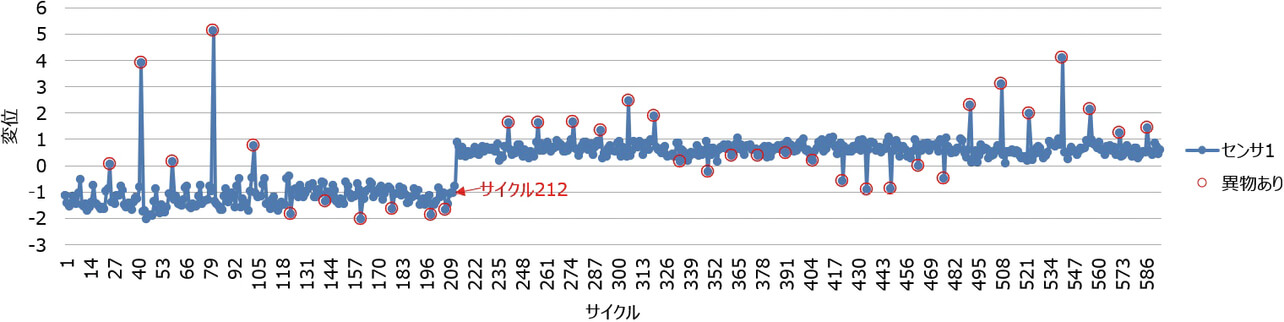
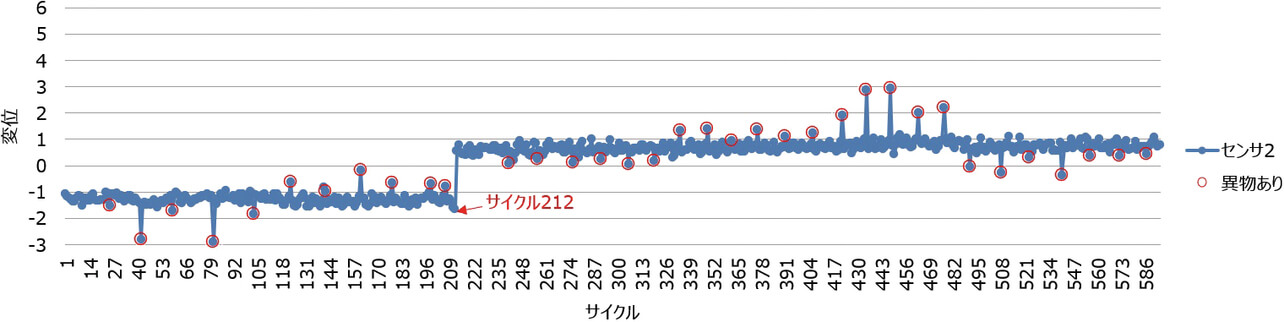
図2、図3の赤丸は、意図的に異物を噛み込ませた時であることを示している。異物がある時は、その前後で異物がない時に比べて、値が突出する傾向が見られる。センサ1の値はプラス側に突出し、センサ2の値はマイナス側に突出する場合と、センサ2の値はプラス側に突出し、センサ1の値はマイナス側に突出する場合がある。実験時は、異物の位置を実験者が決めているため、値の突出の向きは、異物の位置と、2つのセンサとの位置関係に依存していることがわかっている。
図4は、図2、図3のデータの散布図である。異物なしのサンプルは、2つの領域に集まるようにして分布している。この2つの領域は、サイクル212の前後の領域である。また、異物ありのサンプルは、それらの集まりとは異なる特徴を持って分布していることがわかる。
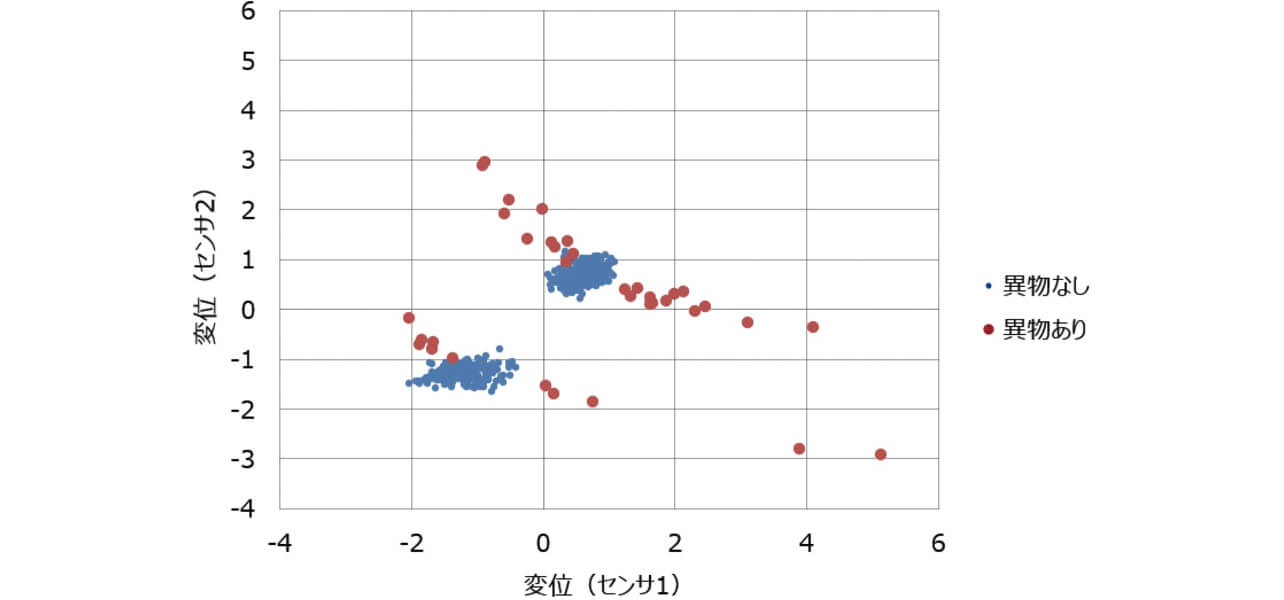
本稿が対象とするAIは、加工の直後に、その加工によって良品・不良品のどちらになるのかを判定することを目的とする。そのためには、加工の後に検査工程を置いて判定するのではなく、加工時のデータだけから判定する。
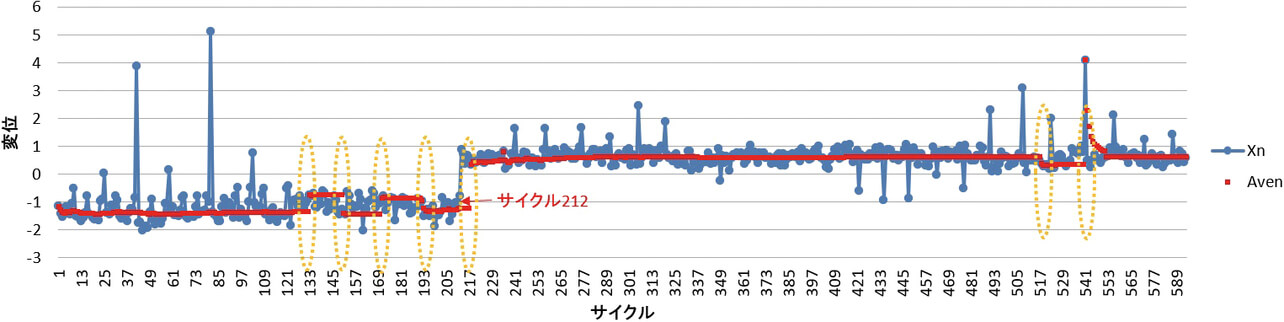
具体的にこのAIで解決したい課題は、図2、図3のようなケースであり、途中で大きな変化が発生している。包装機用AIを開発する際に、このケースに対応する必要があった。図2、図3のデータは、時間の経過と共に、測定した値が記録されている。図2において、サイクル212までは、変位が-2から0の間で推移しているのに対して、サイクル212より後は、変位が0から1の間で推移しているため、このタイミングで、大きな変化があったことが見受けられる。図3においても、同様にして、サイクル212のタイミングで大きな変化が見受けられる。
異常検知の従来手法として、バッチ学習の一種であるMT法5)を使った結果を、図5に示す。学習データとしてサイクル1~24のサンプルを使っている。図5の縦軸は、マハラノビス距離(MD : Mahalanobis’ Distance)である。マハラノビス距離については、3.2.1で説明する。
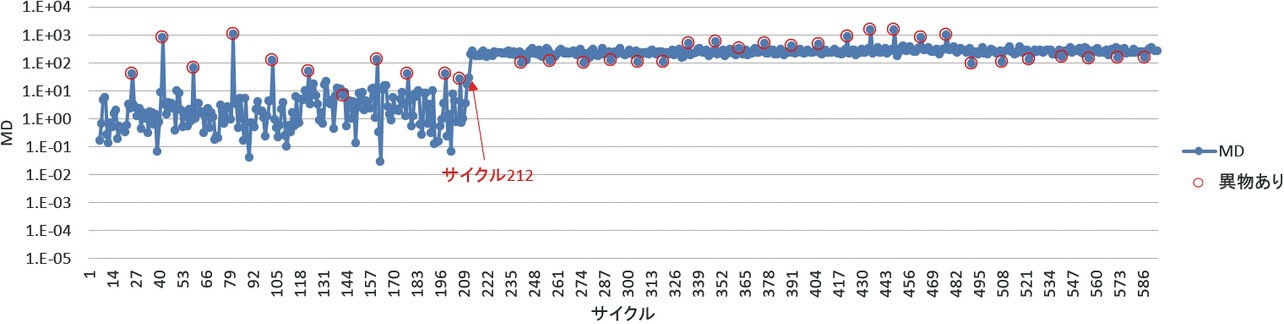
この方法では、サイクル212までで、異物ありと異物なしのサンプルについてMD の値を比べると、異物ありの場合はMD が高いことがわかる。サイクル212までは、MD が1.E+02から1.E+03のあたりであれば、異物ありのサンプルである。サイクル212より後は、異物の有無に関わらず、1.E+02から1.E+03のあたりになっている。例えば、「1.E+01以上なら、不良品と判定」というルールにした場合、サイクル212までは、異物なしのサンプルの多くは「良品」と判定されるが、サイクル212より後は、すべての異物なしのサンプルが不良品と判定されることになり、判定の仕組みとして利用できない。
なお、本例では、機械学習アルゴリズムとしてはMT法を用いたが、問題はバッチ学習というフローに起因して起きているものであり、他の機械学習アルゴリズムでもバッチ学習を用いるならば同様の問題が生じる。
図2、図3のようなケースへの対応としては、まず、サイクル212よりも後に変化が起きたことを、自動で検知することが課題である。さらに、検知をした後に速やかに新しい基準による判定を開始することも課題である。また、包装機は1サイクルが0.1~1秒のオーダーであるため、計算量が少なく、高速で計算できるようにすることも課題である。
3. 提案手法
提案する方法は、課題としている変化を検知した時には、過去の基準を破棄して新たに学習を始める方法とした。また、逐次学習をベースとすることによって、変化を検知した後に速やかに新しい基準による判定を開始できるようにすると共に、高速の計算の課題にも対応することにした。これらにより、前章で示した課題の解決を図っている。
3.1 連を用いた学習フロー
課題の解決には、まず、変化のタイミングを自動で判断する方法が必要になる。この方法として、管理図で「連(れん)」6)と呼ばれる指標を応用することにした。
「連」とは、管理している値が、中心値を0として、プラス側あるいはマイナス側に連続して、一定回数出現した場合に「異常」と見なす指標である。JIS6)では、出現回数が9回となった時を連として定めている。連続して9回プラス側の値が出現した場合、この場合が発生する確率は、

である。このような小さな確率で発生する状態が発生した場合に、偶然その事象が発生したのではなく、「異常なことが起きているので、偶然では起きにくいことが起きている」とみなすのが、連の考え方である。
連の発生を判断するためのフロー図を図6に示す。図6のsxn とは、新しく得られたxn というデータに対し、フローの運用開始前に準備したデータの平均値(Ave )と、標準偏差(Std )から求める値である。この処理は「標準化7)」と呼ばれる。

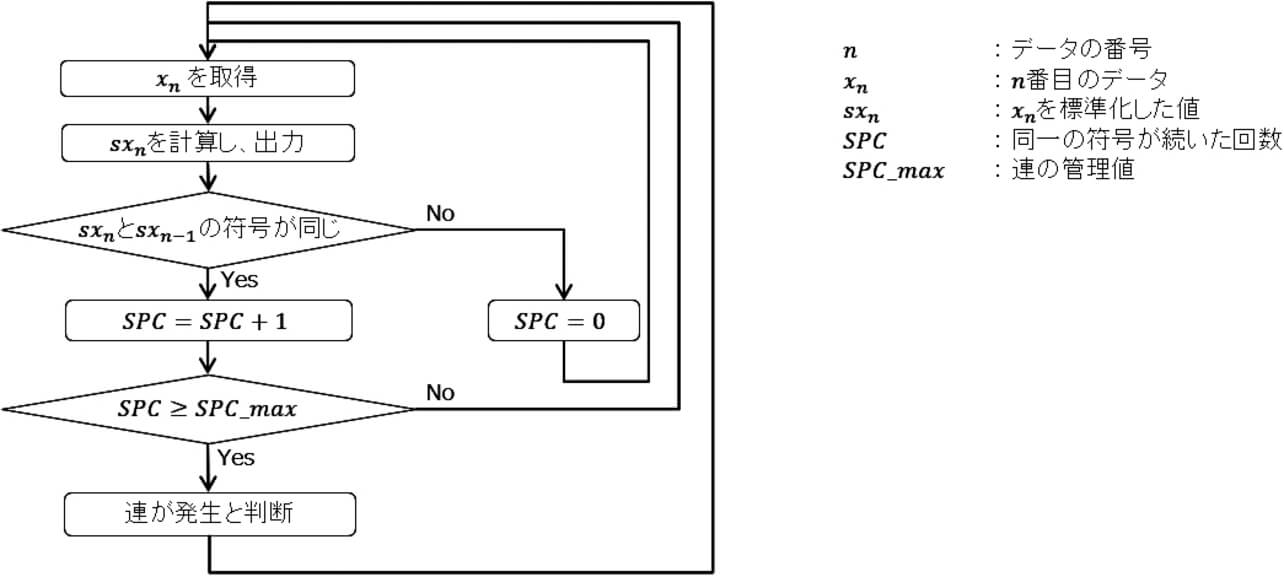
なお、このフローの中では、sxn は、連の発生を抽出するために必要な値として用いているが、sxn は、平均値(Ave )から離れるほど絶対値が大きくなる性質があり、そのサンプルの平均値からの逸脱度を評価するための指標としても、用いることができる。
提案する方法では、「連の発生」を「変化の発生」とみなす。連が発生した時に、過去のデータを破棄して、新たに学習を始める方法に利用している。新たに学習を始めるための処理のフローを、図7に示す。
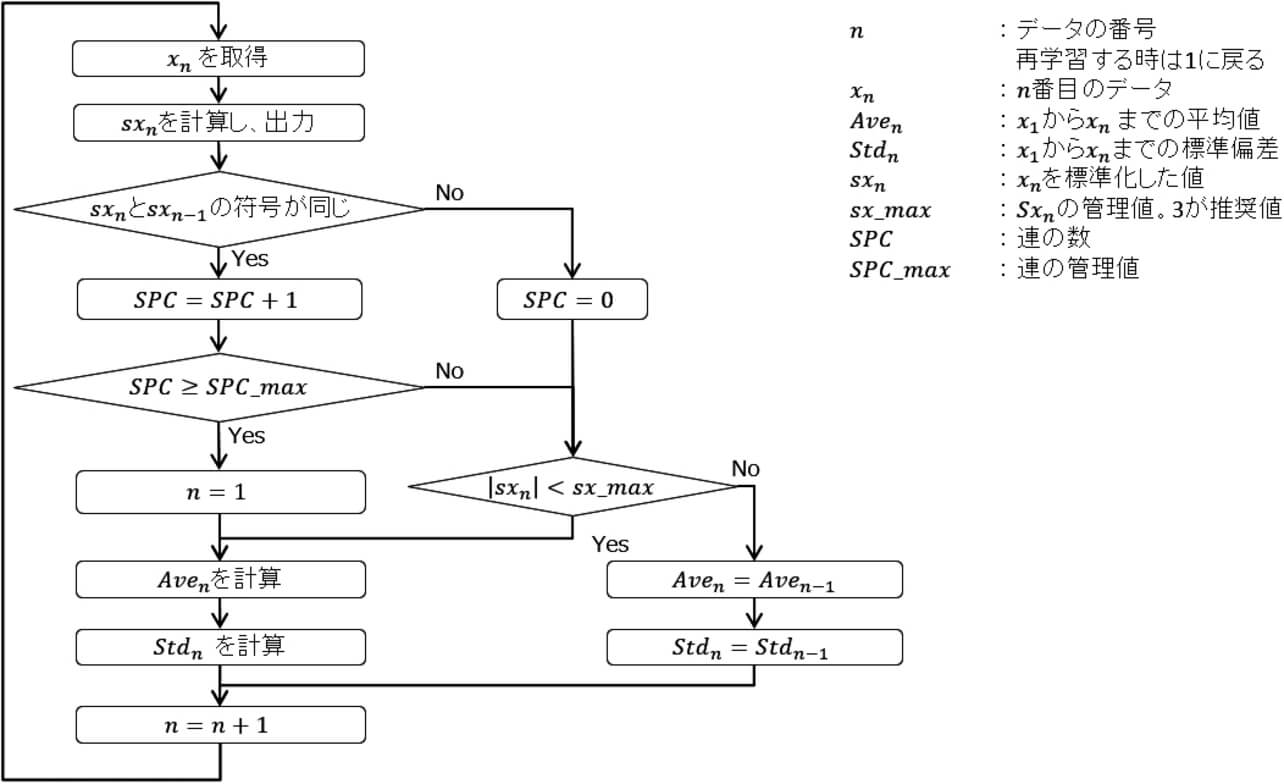
「SPC ≥ SPC _max 」というステップによって、連の成立を判定する。連が成立した場合、「n =1」となるが、こうすることで、過去の学習を破棄して、新たに逐次学習が始まるようにしている。
「|sxn |<sx_max 」というステップは、得られたsxn が外れ値かどうかを判断するためのステップである。標準化したデータを外れ値と判断するための基準は、3シグマのルール6)を参考にして、3を推奨値とした。外れ値と判断された場合、平均値と標準偏差の値を再計算しないようにしている。こうすることで、外れ値の影響を受けにくい方法にした。
平均値を逐次学習で求める式は、式(3)である。n −1番目までの平均値Aven −1とn 番目のサンプル値xn を使って、n 番目までの平均値Aven を求める式になっている。式(3)は、一般に知られている平均値の計算式から、逐次学習の式を導いている。Ave0 = 0である。

標準偏差を逐次学習で求める式の導出の前に、共分散を逐次学習で求める式を導出する。変数l と変数m について、n 番目までのサンプルまでの共分散を

まず、

ここで、

である。よって、

となり、共分散を求める逐次学習の計算式が求まる。
分散は、共分散の式においてm = l の場合である。n番目のサンプルまでの分散をVarn と記述した時に、Varn を逐次学習で計算する式は、式(5)より、

である。Var0 = 0である。
標準偏差は、分散の平方根である。n番目のサンプルまでの標準偏差をStdn と記述した時に、Stdn を逐次学習で計算する式は、式(6)より、

である。Std0 = 0である。
データを逐次的に標準化7)する方法は、逐次学習で求めた平均値と標準偏差を用いると、式(8)になる。ここで、sxn とは、標準化されたn番目のサンプル値である。

3.2 変数が複数ある場合の方法
前節は、変数が1つの場合の方法である。これを複数の場合に拡張した場合のフロー図が、図8である。
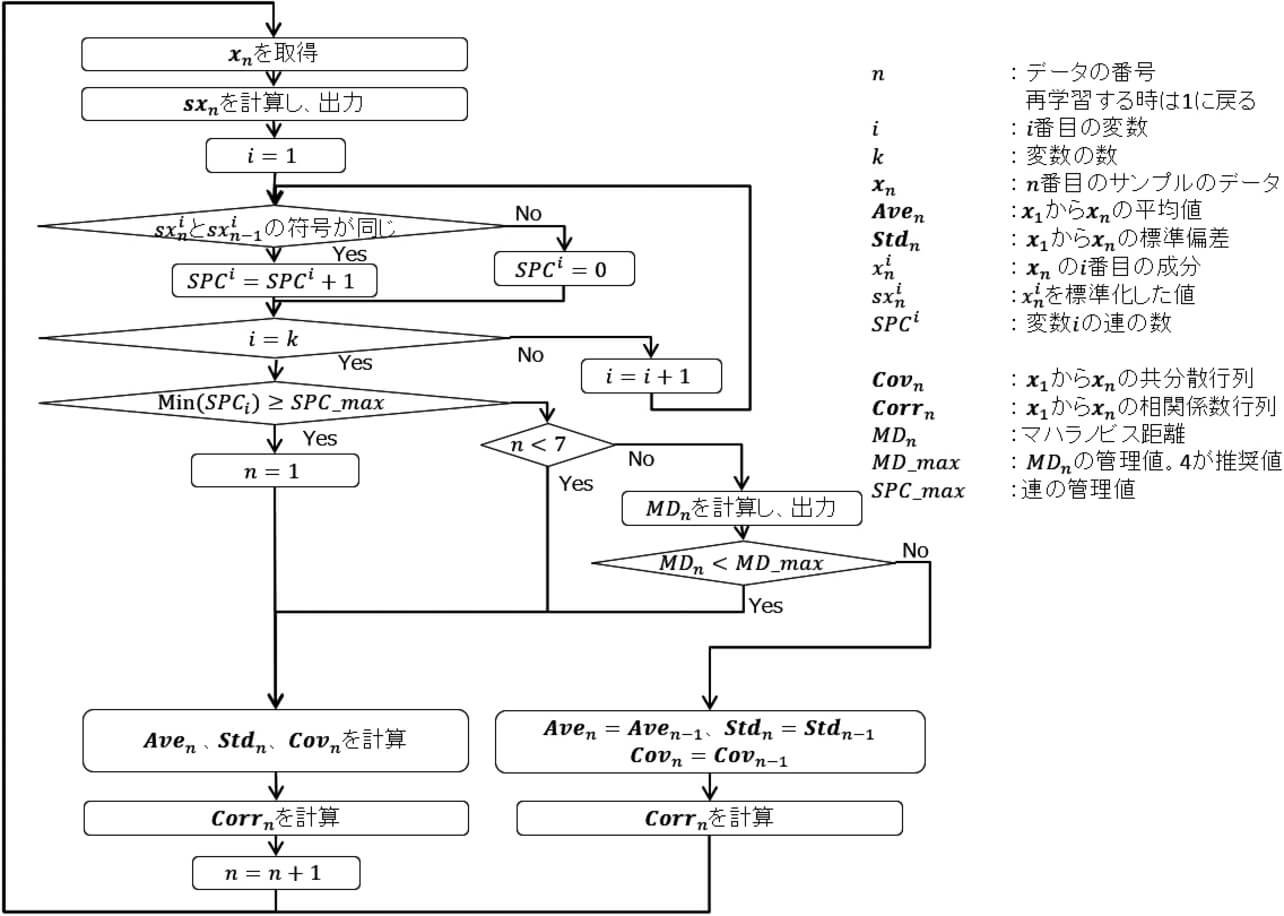
3.2.1 マハラノビス距離
前節では、平均値からの逸脱度を示す指標と、外れ値の影響を受けにくい方法にするための値として、sxn という指標を使っている。変数が複数ある場合に、sxn の役割を持つ値として、提案手法では、マハラノビス距離を使用している。
マハラノビス距離とは、例えば、図9の矢印の長さであり、基準点と各サンプルの距離を表している。図9では、例として異物なしのサンプルが集まっている領域の1点を基準点としているが、実際の計算では、学習に使用したサンプルにおける各変数の平均値を基準点の座標とする。
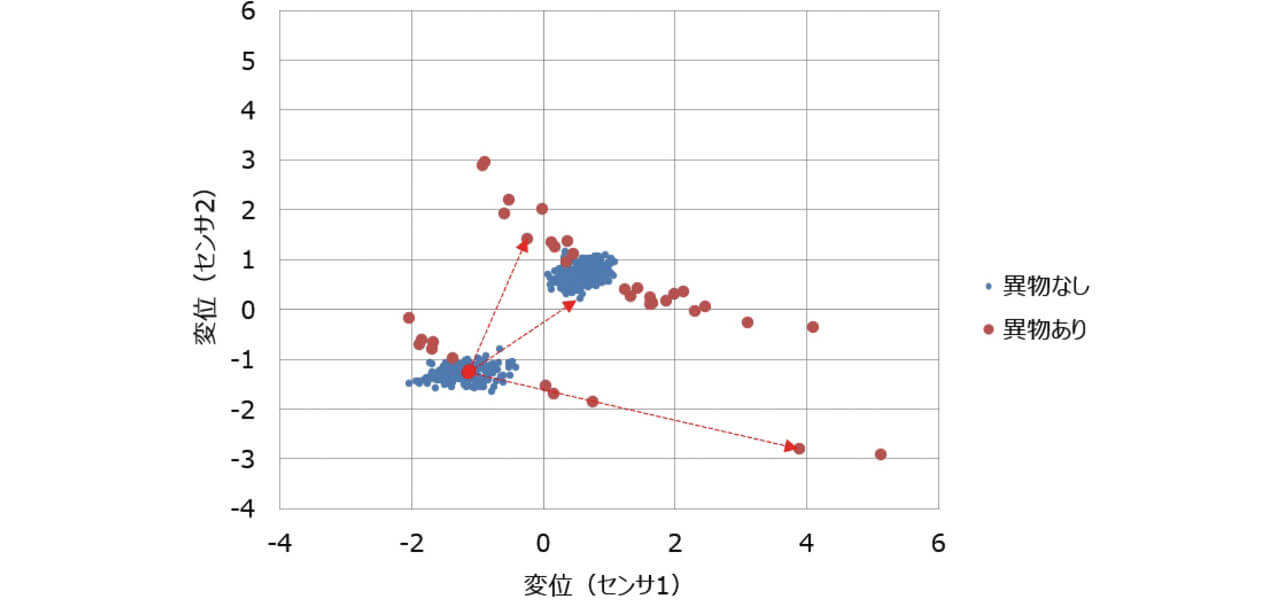
マハラノビス距離を、本手法で使用する場合、まず、変数が1つの時と同じように、平均値と標準偏差を逐次学習する必要がある。また、共分散も逐次学習する必要がある。共分散を逐次学習で計算する式は、既出の式(5)である。
共分散から、相関係数

マハラノビス距離を求める式として、変数の数が変化しても管理値を変えないことが製造現場で使用する際に便利であることを考慮して、ここでは、品質工学のMT法における定義式5)を採用することにした。マハラノビス距離(MD )の計算式を、式(10)に示す。ここで、sxn とは、n 番目のサンプルのデータであり、ベクトルxn を各変数について、標準化の処理をしたベクトルとして表している。なお、xn ではなくsxn を使用すると、共分散行列は相関係数行列になる8)ため、n −1番目のサンプルまでのデータを使って作成した相関係数行列Corrn −1を使用している。

2変数の場合、式(10)に含まれる逆行列の部分は、

となる。

の公式を使うと、

と書き下すことができる。
図2、図3のデータは2変数の場合であり、4章における提案手法の実験では、この公式を使って逆行列の部分を計算している。
なお、n ≤ 3では、以下に示す理由により、マハラノビス距離は計算できない。
- n = 1の時 前の周期のデータがない。
- n = 2の時 前の周期までのデータが1サンプル分となり、相関係数が計算できない。
- n = 3の時 前の周期までのデータが2サンプル分となり、相関係数は1になるので、逆行列が計算できない。
よって、原理的にはn ≥ 4ならば、マハラノビス距離が計算できるのであるが、本手法では、n ≥ 7の場合にマハラノビス距離を計算するアルゴリズムとしており、フロー図の中で「n < 7」と表現している。この条件は、サンプル数が少ないと、標準偏差の推定値が過小に計算される可能性があることから定めている。標準偏差が小さいと、新しいサンプルが「外れ値」と判定されやすくなる。「外れ値」と判定されると、そのサンプルのデータは、逐次学習に利用されないアルゴリズムにしているため、いつまでも過小に計算された標準偏差が使われ続け、本当は外れ値ではないサンプルが「外れ値」と判定され続けてしまう可能性がある。
この点を考慮して、フロー図では、「n < 4」ではなく、「n < 7」と置いているが、これは仮の値である。この値は、小さいと、外れ値ではないサンプルを「外れ値」と判定する誤りが起きやすくなる。一方で、大きいと、マハラノビス距離が計算されないサンプルの数が増えやすくなるリスクがある。
3.2.2 変数が複数の場合の連
前節のように、1変数の場合は、「標準化した値がプラス側で連続する。または、標準化した値がマイナス側で連続する。」というルールで連が定義されている。
提案手法では、変数が複数の場合の連を定義した。まず、それぞれの変数に対して個別に連を判断し、いずれかが連になった場合に、複数の変数における連として、定義することにした。この部分は、フロー図において、

と記した部分が相当する。
3.2.3 外れ値の判定の方法
外れ値の判定については、多変量の外れ値を判定する指標として、マハラノビス距離で行うこととした。判定値は、MT法における判定基準9)を参考にして、4を推奨値とした。外れ値と判定されたサンプルのデータは、逐次学習に含まないことで、外れ値の影響を受けにくい方法にした。
4. 実験
2章で示した包装機のデータに対して、提案手法を適用した結果を述べる。
4.1 連の管理値の調整
図10は、図2のデータxn に、平均値Aven の計算結果を赤の点で重ね合わせたグラフである。平均値Aven は、サイクル212の後に、大きく変化しており、これは狙い通りの計算結果となった。しかし、図10に黄色の点線で囲んだ部分のように、サイクル212の後以外の部分でも、平均値が非連続的に変化している部分が散見された。サイクル212以外の変化については、比較的短期間のみの変化となっている。
ここで、提案手法の利用方法としては、比較的短期間の変化も検知する方法と、比較的短期間の変化は検知しない方法が考えられる。
2章で示した課題から要請されるのは、後者であるため、以降、比較的短期間の変化は検知しない方法を用いる。そのためには、連を9よりも長めにした方が良いと考えられる。
図11は、試行として、連の管理値を25に変更した場合である。この変更をすれば、平均値が非連続的に大きく変化するのは、サイクル212の後だけになった。
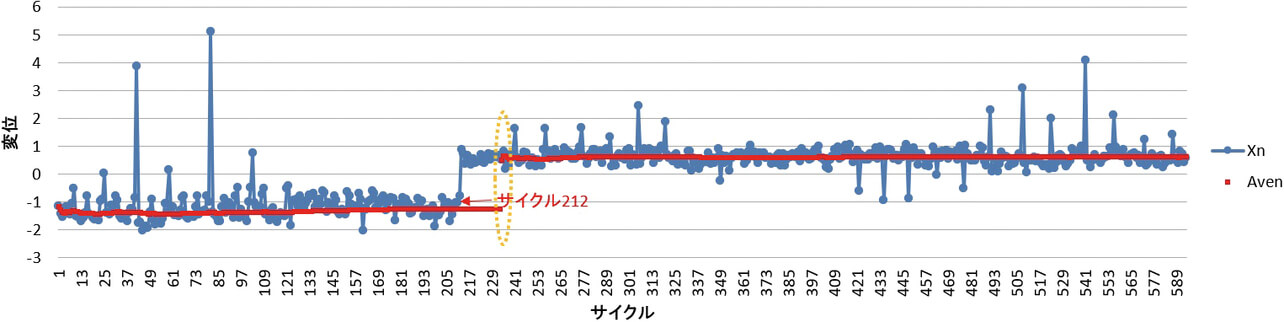
本稿で明らかになったのは、連の管理値の調整が重要なことである。この管理値は、小さくすれば、平均値の非連続的な変化の頻度が増加し、変化の直後の「n < 7」の期間は判定不能となるため、判定不能なサンプル(=6×変化点の数)が増加する。一方で、この管理値を大きくすれば、連の成立を判断するために必要なサンプル数(=連の管理値×変化点の数)が多くなり、そのサンプルについては、変化前の基準で扱われるため、適切な判定がされない。この関係を試算すると、表1となる。判定不能なサンプルと、変化前の基準が適用されるサンプルの合計値は、表1の中では、連の管理値が25の時が最も少ない。このことから、連の管理値は、大き過ぎず、かつ、小さ過ぎないように調整する必要があることがわかる。
| 連の管理値 | 変化点の数 | 判定不能な サンプル |
変化前の基準が適用されるサンプル | 合計 |
|---|---|---|---|---|
| 9 | 7 | 42 | 63 | 105 |
| 25 | 1 | 6 | 25 | 31 |
| 50 | 1 | 6 | 50 | 56 |
| 75 | 1 | 6 | 75 | 81 |
4.2 従来手法との結果の比較
提案手法を実施し、従来手法とも比較した。比較対象とした従来手法は、以下に、「バッチ学習」と「逐次学習」と呼ぶ2種類の方法である。いずれもマハラノビス距離MD を計算する点は共通している。
提案手法では、連の判定値は4.1の結果を元にして、25に設定して実行している。
バッチ学習は、1~24サイクルのサンプルを学習用データとし、これらのデータの平均値、標準偏差、相関係数を元にして、MD を計算する。
逐次学習は、1サイクル目から平均値、標準偏差、相関係数を順次計算して更新し、それらによりMD を計算する方法である。提案手法との違いは、連が発生しても「n = 1」とはしない点である。
結果を図12に示す。「異物なし」とは、異物を噛み込ませていないサンプルのグループである。「異物あり」とは異物を噛み込ませたサンプルのグループである。これらのグループについて、MD の分布を比較した。バッチ学習と、逐次学習では、異物ありとなしの分布が大きく重なるのに対して、提案手法では、分布が比較的分かれている様子がわかる。
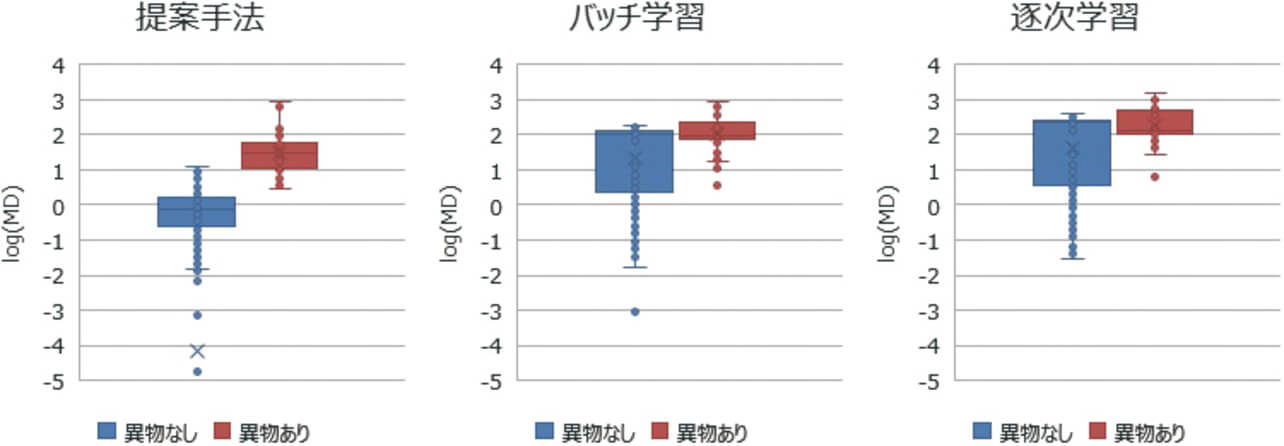
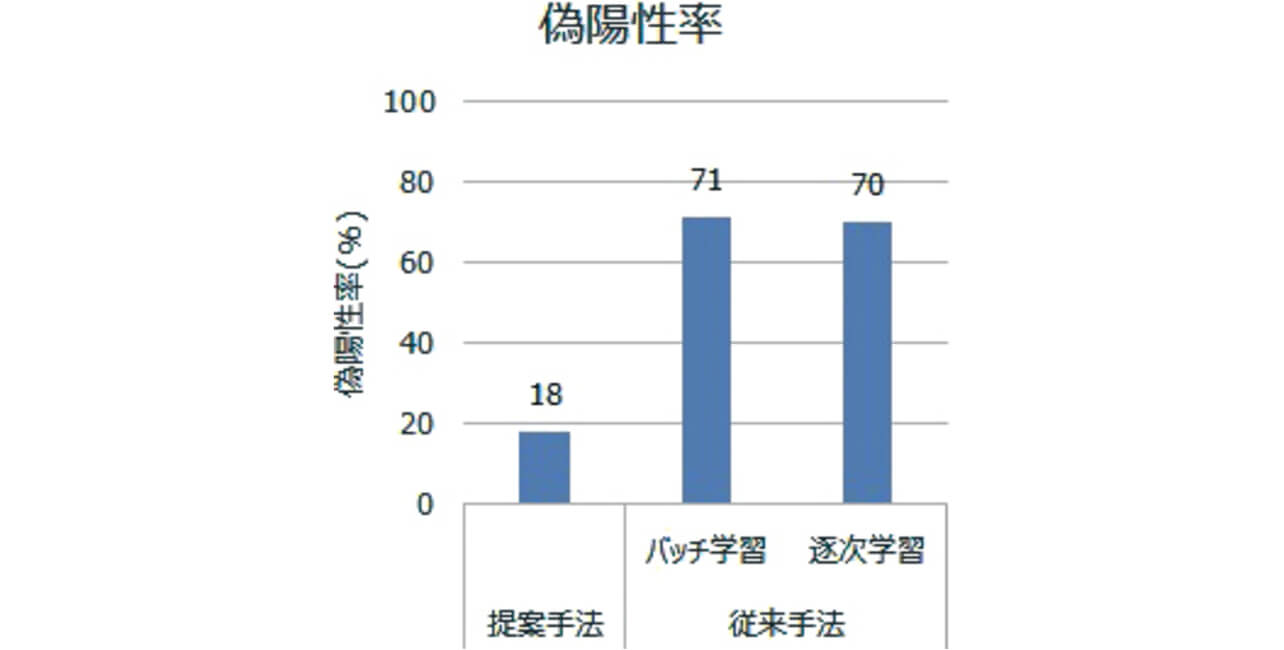
図13は、偽陽性率であり、異物ありのサンプルのマハラノビス距離MD の最小値を基準とした場合に、異物なしのサンプルで、その値よりも高くなるサンプルの割合を表している。つまり、異物ありのサンプルは、確実に不良品と判定されるように基準を決めた場合の誤判別率である。提案手法は18%であり、従来手法は、いずれも約70%であることから、約50%改善できることが確認できた。よって、図2、図3で示したデータの変動に対して、提案手法が有効であることを確認できた。
5. むすび
製造現場におけるデータには、急激な変化が起きることがあり、その対応は、製造現場における機械学習適用の課題の一つである。
本稿では、その課題に対して、逐次学習のアルゴリズムや、管理図における安定状態の指標のアイディアを応用することで、変化に自動的に追従して対応することができる異常判定のアルゴリズムを提案した。包装機を使った実験データに対して、このアルゴリズムを適用し、提案手法による偽陽性率が18%であるのに対し、従来手法として比較した2種類は、いずれも約70%であり、約50%改善できることが確認できた。
本手法を実施する場合は、連の長さの設定がユーザに委ねられている。本手法では、変動の検知が連を使って自動に行われ、学習データの取得が逐次学習によって自動に行われるが、この調整についても、対象とする現象の性質に合わせて、自動的に設定することが課題である。
また、本手法は、急激な変化が時々発生するものの、その前後では一定期間にわたって、平均的な値が維持される状況を想定している。一定期間にわたって平均的な値が維持されず、常に変化を続けているような現象については、本手法は対応できない。このような現象については、別のアルゴリズムを考案することが課題である。
今後は、上記の残された課題も踏まえ、この技術をオムロンのコントローラに取り入れる等、顧客課題解決への貢献を検討していく。
参考文献
- 1)
- オムロン株式会社. “ソリューションAI.” https://www.fa.omron.co.jp/solution/technology-trends/ai/(Accessed: Dec. 1, 2022).
- 2)
- 溝口理一郎, 石田亨, 人工知能, オーム社, 2013.
- 3)
- 海野裕也, 岡野原大輔, 得居誠也, 徳永拓之, オンライン機械学習, 講談社, 2015.
- 4)
- 坂元佑気, 中村芳行, 杉岡真行, “リアルタイム処理可能な特徴量を用いた機械学習によるねじ締め底付き不良検知の事例,” OMRON TECHNICS, vol. 55, no. 1, pp. 35-44, 2023.
- 5)
- 宮川雅巳, 永田靖, タグチメソッドの探究, 日科技連出版社, 2022.
- 6)
- 日本規格協会, JISハンドブック 品質管理, 日本規格協会, 2022.
- 7)
- 荻原大, データ分析の進め方及びAI・機械学習導入の指南, 情報機構, 2020.
- 8)
- 涌井良幸, 涌井貞美, 図解でわかる多変量解析, 日本実業出版社, 2001.
- 9)
- 立林和夫, 入門MTシステム, 日科技連出版社, 2008.
本文に掲載の商品の名称は、各社が商標としている場合があります。














