サーボドライブシステムにおける高周波漏れ電流による伝導ノイズの解析手法検討
- パワーエレクトロニクス
- EMI
- 伝導ノイズ解析
- シミュレーション
- サーボドライバ
労働人口の減少、および脱炭素化に向けた生産現場の省エネルギー化が、社会的に大きな課題となっている。それに向けて、モータの回生電力を有効活用する方法が提案されており、サーボドライブのDC給電化が期待されている。一方で、現在主流のAC給電システムと比較し、サーボドライブDC給電システムは、サーボドライブが発生したノイズが他のサーボドライブに回り込みやすく、誤動作の問題が懸念される。特に、サーボドライブとモータ間のシールドケーブルからの高周波漏れ電流による伝導ノイズが問題となる。この伝導ノイズは、サーボドライブの開発期間長期化の要因となることから、開発上流工程で対策検証できる解析手法が必要である。
本論文では、サーボドライブの開発期間短縮を目的として、将来のDC給電システムへの展開を視野に入れた、AC給電システムにおけるシールドケーブルからの高周波漏れ電流が系統や他機器へ与える影響を評価可能な伝導ノイズ解析手法を検討した。本手法により、サーボドライブシステムに対して、シールドケーブルのケーブル長・軸数を変更したときの伝導ノイズの変化傾向を再現した。
1. まえがき
近年、労働人口の減少により、生産現場へのロボットの導入が求められている。一般的に、ロボットには数軸から数十軸の同期性と高速高精度制御を備えたサーボドライブと電動機(モータ)が採用される。一方で、脱炭素化に向けた社会的な要請から、生産現場の省エネルギー化が大きな課題となっている。産業用モータによる年間の電力消費量は、産業部門の消費電力量の約75%を占めると推計されており1)、省エネルギー化に向けて、モータの回生電力を有効活用する方法が提案されている2)。
その具体的な方法の一つとして、現在はAC給電が主流であるサーボドライブのDC給電化が検討されている3)。図1にサーボドライブAC給電システムとDC給電システムの構成を示す。
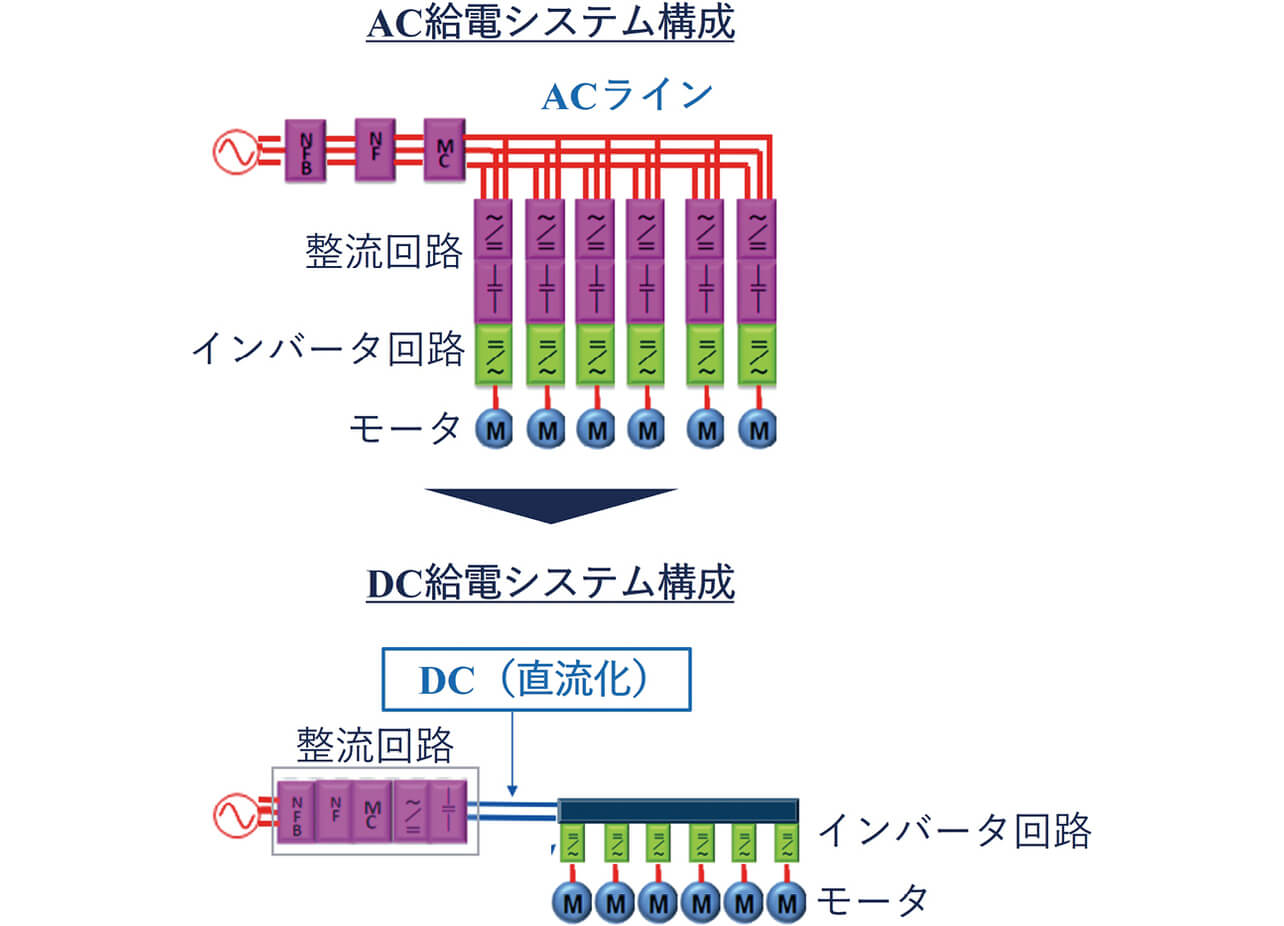
AC給電システムは、サーボドライブ1台に整流回路とインバータ回路が搭載され、サーボドライブ1台にモータ1台が接続される構成である。数軸~数十軸の多軸のサーボドライブとモータが、ACラインに並列接続される。これに対し、DC給電システムは、整流回路が集約された構成である。整流回路によるAC/DC変換後のDCバスに多軸のインバータ回路とモータが並列接続される。
DC給電システムは、回生電力の有効活用に加え、小型化が可能で、軸数増加にも有利な構成であるといえる。一方で、インバータ回路が整流回路を介さず、DCバスに並列接続されるため、AC給電システムよりもインバータ回路から発生した電磁ノイズが他のインバータ回路に回り込みやすく、誤動作の問題が懸念される。このノイズ対策は、商品開発期間長期化の要因となる課題であることから、開発上流で検証できる解析手法が必要である。具体的には、解析を活用して、ノイズフィルタ構成や共振対策を検討する。
サーボドライブのAC給電システムとDC給電システムの回路構成要素は共通であり、AC給電システムに対して構築した解析手法は、DC給電システムにも展開可能である。よって、本論文では、DC給電システム検討の前段階として、AC給電システムを検討対象とする。
モータの高速高精度な位置・速度・トルク制御のために、サーボドライブのインバータ回路にはパワー半導体素子を用いたPWMインバータが採用される。近年、パワー半導体素子に、炭化ケイ素(SiC)や窒化ガリウム(GaN)のような次世代パワー半導体の採用が進められており、PWMインバータのキャリア周波数の高周波化が進んでいる。この高周波化に伴い、サーボドライブとモータ間のケーブルおよびモータの浮遊容量を通して接地線(GND)に流れる高周波漏れ電流の増加による電磁ノイズの問題が指摘されている4)。
これまで、PWMインバータのスイッチングによりモータ巻線の浮遊容量を通して接地線に流れる高周波漏れ電流について、定量的な理論検討が行われ、等価回路モデルが示されている4)。この高周波漏れ電流により生じる電磁ノイズ現象の1つに雑音端子電圧がある。PWMインバータが発生する雑音端子電圧をシミュレーションにより定量的に推定する手法が提案されている5,6)。
この雑音端子電圧は、インバータのスイッチングに伴うコモンモード電圧の変動に起因して、モータの固定子巻線-GND間の浮遊容量を流れる漏洩電流によるコモンモードノイズが主要因であることが示されている5,7)。また、このコモンモードノイズの周波数帯域は数MHz以下であり、主に1 MHz帯まで支配的であることが示されている7)。
近年、低圧インバータにおいて、サーボドライブとモータ間のケーブルにシールドケーブルが採用されることが主流になってきている。シールドケーブルは、モータ動力線と外部シールド(GND)間に大きな浮遊容量が生じることから、高周波漏れ電流が大きくなることが知られている。一般的に、生産現場のロボットにサーボドライブシステムが採用される場合、サーボドライブとモータの軸数およびケーブル長が増加する傾向がある。このため、シールドケーブルが多軸化・長尺化したときの高周波漏れ電流が系統や他の機器に与える影響を評価することが重要である。
低圧インバータへのシールドケーブル適用について、コモンモードノイズの観点から検討されている8)。一方で、シールドケーブルの高周波漏れ電流が系統に与える影響(=雑音端子電圧)や軸数・ケーブル長の増加によるノイズの増加傾向を評価できるモデルは示されていない。
本論文では、サーボドライブシステムの開発期間短縮を目的として、AC給電システムの伝導ノイズ解析手法を検討する。特に、1.5MHzまでの周波数帯域において、サーボドライブシステム共通の問題であるシールドケーブルからの高周波漏れ電流が、系統や他機器へ与える影響を評価可能な解析手法を示す。本手法により、既存のサーボドライブAC給電システムに対して、シールドケーブルのケーブル長・軸数を変更したときの雑音端子電圧の変化傾向を再現した。
2. 伝導ノイズ解析手法
2.1 サーボドライブAC給電システムの構成
図2に、サーボドライブAC給電システムの回路図を示す。
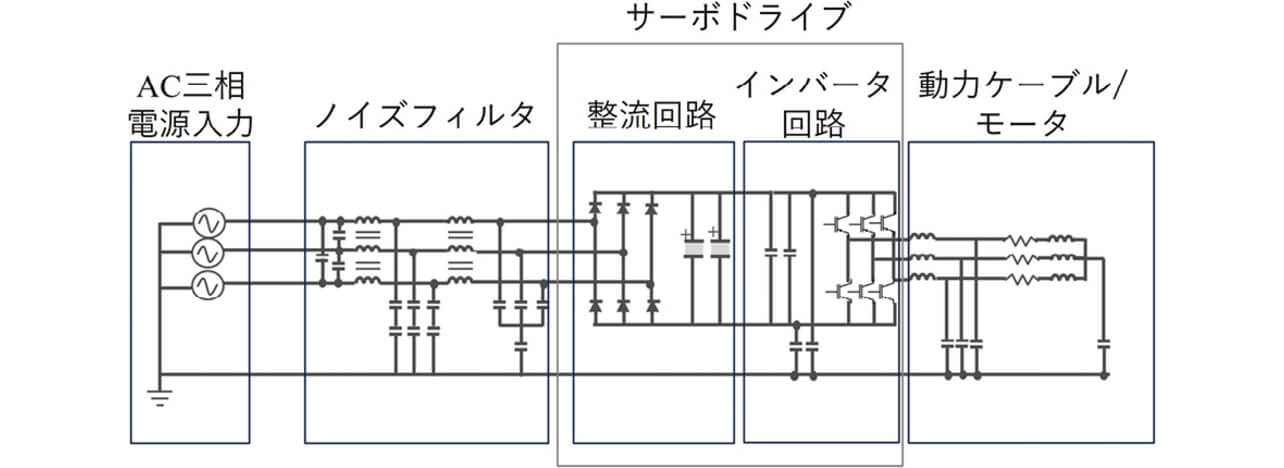
図2において、三相交流電源側(系統)への伝導ノイズの流出を防止するためのノイズフィルタがあり、その後段の整流回路により交流入力が直流に変換される。次に、直流をインバータ回路のスイッチングにより三相のPWM波形に変換し、動力ケーブルを通して、モータ(負荷)に供給する。
2.2 シミュレーションモデル
サーボドライブAC給電システムの伝導ノイズ解析モデルを図3に示す。なお、回路シミュレータはPSIM(Altair社)を用いる。
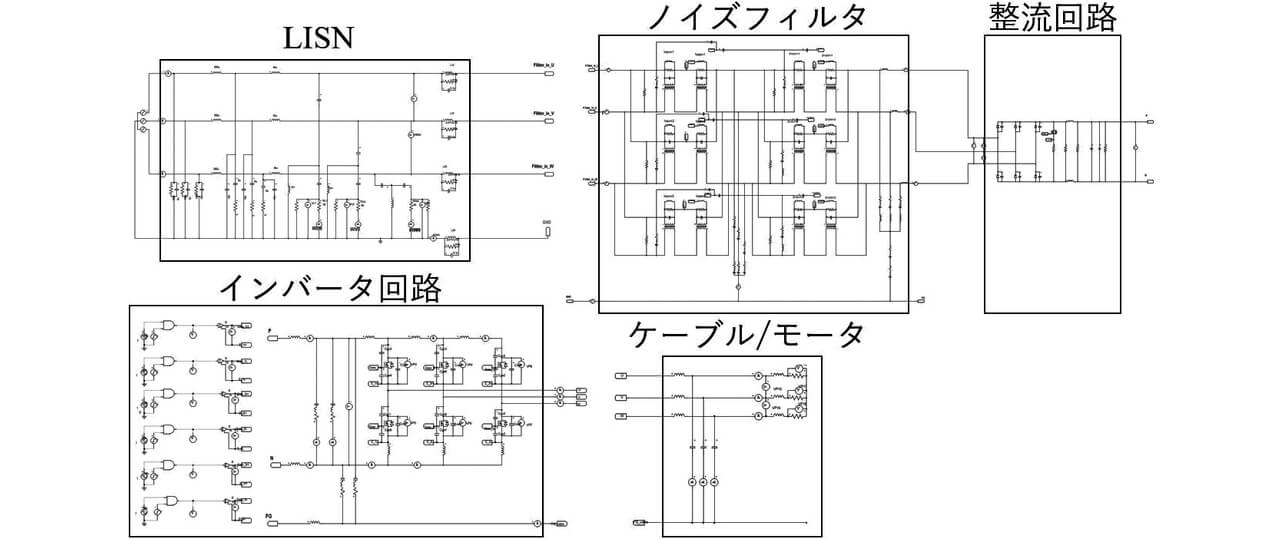
表1に、主要なシミュレーション条件を示す。
| 項目 | パラメータ |
|---|---|
| 電源入力 | 3 Φ AC 240 V/50 Hz |
| 出力電力 | 200 W |
| ノイズフィルタ | FSB-30-254-HU(コーセル社) |
| 整流回路 | ダイオード整流 |
| 平滑回路 | 電解コンデンサ |
| キャリア周波数 | 8 kHz |
| 動力ケーブル | シールドケーブル |
このモデルをシミュレーションすることにより雑音端子電圧を評価する。これまで、インバータが発生する雑音端子電圧のモデルは、複数報告されている5,6)。本報告におけるモデルの基本構成はそれらの文献を基本としており、ここでは概要のみ述べる。
雑音端子電圧は、LISN(疑似電源回路網)を交流電源とサーボドライブの間に接続し、LISNのハイパスフィルタを通して雑音端子測定用端子から出力されるノイズ電圧を測定する。本モデルでは、LISNを等価回路としてモデル化している。図4に、LISNの等価回路モデルを示す。
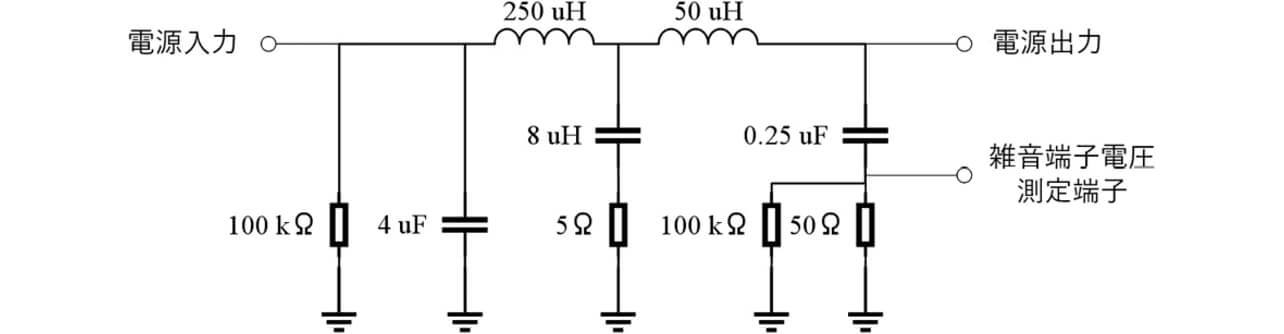
雑音端子電圧は150 kHz~30 MHzの周波数帯で伝導ノイズを評価するため、受動部品および基板パタンの等価回路モデルはその帯域でのインピーダンス特性を再現する必要がある。図5に、受動部品の等価回路モデルを示す。
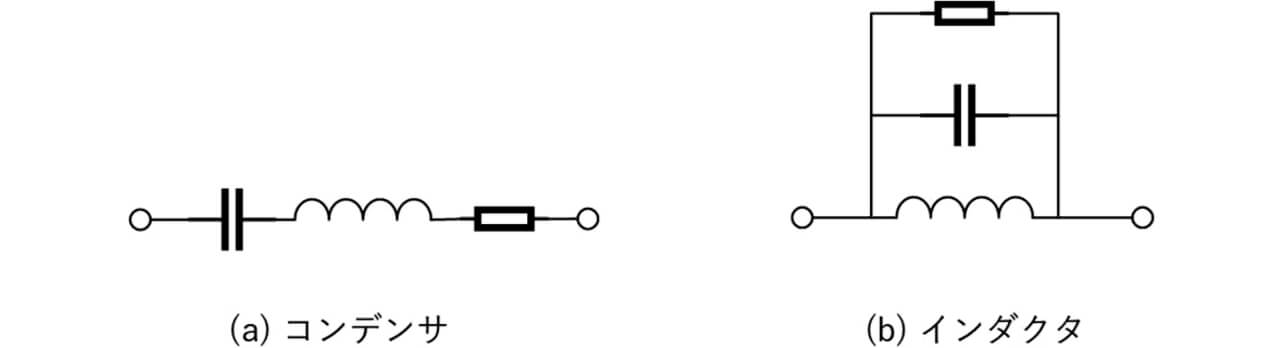
等価回路モデルの回路定数は、ネットワークアナライザで測定した受動部品のインピーダンス周波数特性から算出できる。また、基板パタンの等価回路モデルは、パタン長からの簡易計算または電磁界シミュレーションで算出できる。
3. シールドケーブルの高周波漏れ電流モデル化
3.1 モデル化の方針
サーボドライブのインバータ回路が発生する伝導ノイズの主要因は、インバータのパワー半導体素子と接続されたモータ巻線やケーブルなど機構部品とGND間の浮遊容量を通して流れる高周波漏れ電流によるコモンモードノイズである。特に、ケーブルがシールドケーブルである場合、配線とGNDに接地されたシールドの間に数10 nHオーダの大きな浮遊容量が生じ、コモンモードノイズの主要な伝搬経路となる。これは、モータ巻線とGND間の浮遊容量より1桁大きな値である。シールドケーブルの浮遊容量はケーブル長に比例するため、今後のサーボドライブとモータの軸数とケーブル長の増加に伴い、浮遊容量がより増加すると考えられる。以上より、シールドケーブルの長さや軸数の変更に対するコモンモードノイズの増減と周波数特性を再現することをモデル化の方針とする。
高周波漏れ電流によるコモンモードノイズは1 MHz帯までが支配的である7)。よって、本検討では1.5 MHzまでを評価対象とする。シールドケーブルは一般的に分布定数回路でモデル化される。ケーブルモデルを分布定数回路とするか、集中定数回路とするかは周波数とケーブル長の関係により決まり、その境界は明確ではないが、経験則よりケーブル長が1/4波長となる周波数が、集中定数と見なせる上限の周波数と言われている。一般的なサーボドライブシステムで用いられる最大ケーブル長は50mであるので、本検討ではケーブル長の上限を50mとする。これは、1.5 MHzの1/4波長に相当するので、本検討ではケーブルを集中定数回路でモデル化できると仮定する。ケーブルモデルを集中定数回路で表せれば、ノイズ解析の見通しが良くなり、特にノイズ伝導経路の解析において有用である。
3.2 スイッチング動作
シールドケーブルの配線とシールド間の浮遊容量を通してGNDに流れる高周波漏れ電流は、インバータのスイッチングに伴うコモンモード電圧変動に起因する。したがって、コモンモード電圧変動が最大になるスイッチング動作の時、高周波漏れ電流は最大となる。伝導ノイズシミュレーションモデルにおいて、インバータのスイッチング波形はコモンモード電圧変動が最大となるスイッチング波形とした。
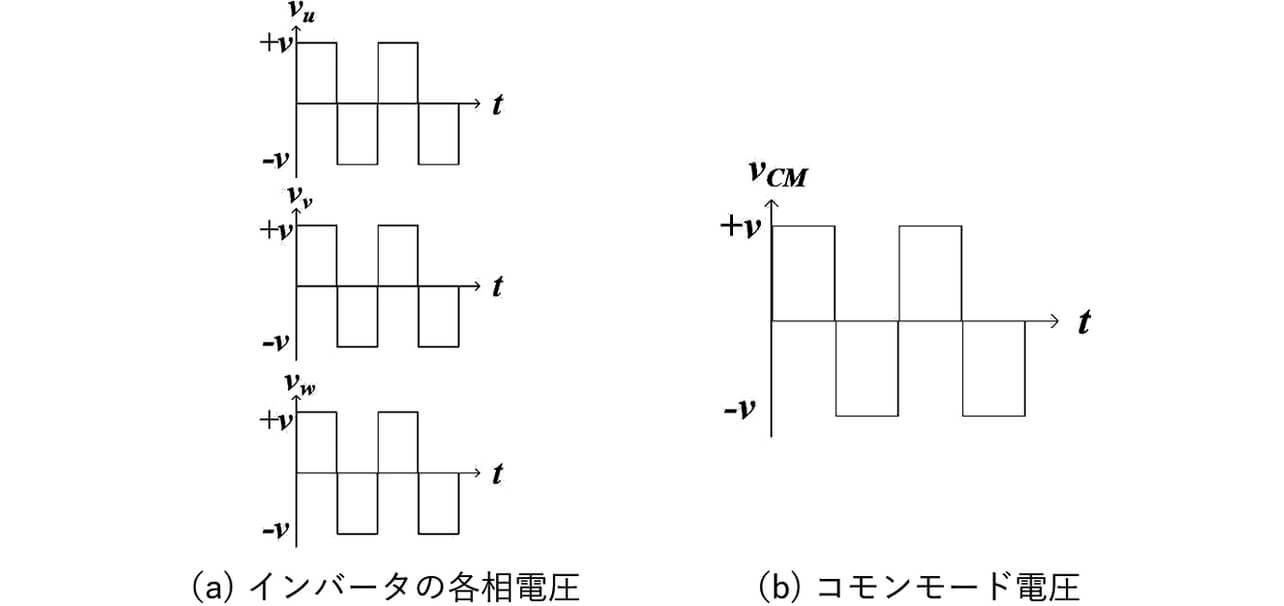
インバータのスイッチングに伴うコモンモード電圧は(1)式で表される。

vu, vv, vw :インバータの各相電圧
vCM :コモンモード電圧
コモンモード電圧vCM の振幅が最大となるのは、サーボロック動作のときであり、この動作時の雑音端子電圧で議論をすすめる。図6にインバータ回路を、図7にインバータのサーボロック動作を示す。
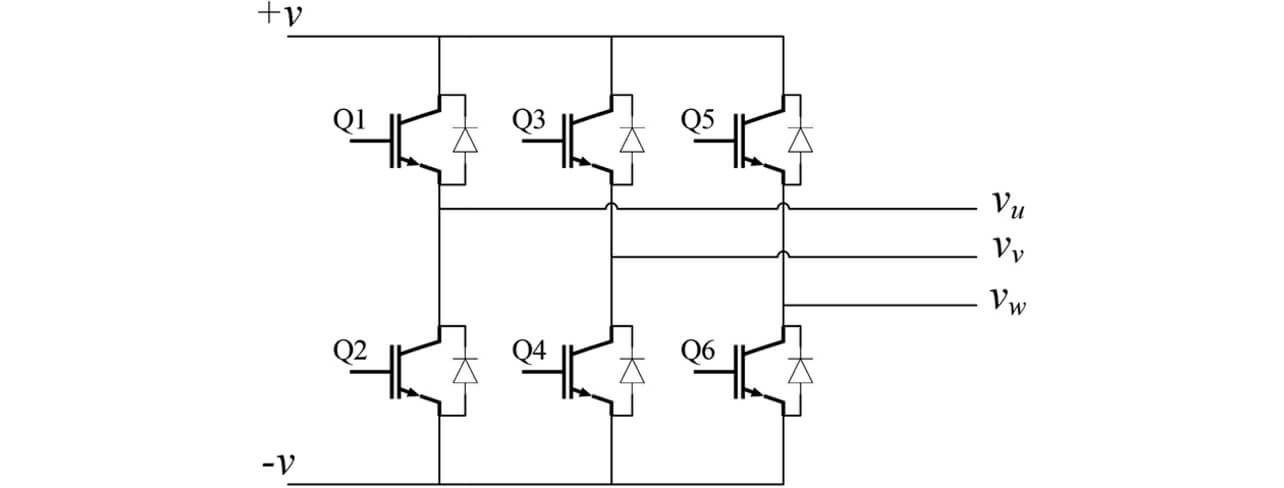
3.3 ケーブル長・軸数に対するノイズ増減の再現
これまで、同一の電源に並列接続された複数台のインバータを同時動作したときに発生する伝導ノイズに関する理論検討がなされている9,10)。同一の電源にインバータが複数台並列接続される構成は、サーボドライブとモータが多軸化されたシステムと同等の構成であり、シールドケーブルの浮遊容量はインバータ並列台数(軸数)に比例して増加する構成である。一方で、いずれの報告においても、ノイズフィルタを含まないモデルでの理論検討がなされており、ノイズフィルタを含んだ場合の軸数に対する雑音端子電圧の理論式は示されていない。そこで、本論文では、まずノイズフィルタを含む場合における雑音端子電圧について理論式を導出し、ケーブル長および軸数と雑音端子電圧の関係式を明らかにする。
図8に、図2に示したサーボドライブAC給電システムのコモンモード等価回路を示す。
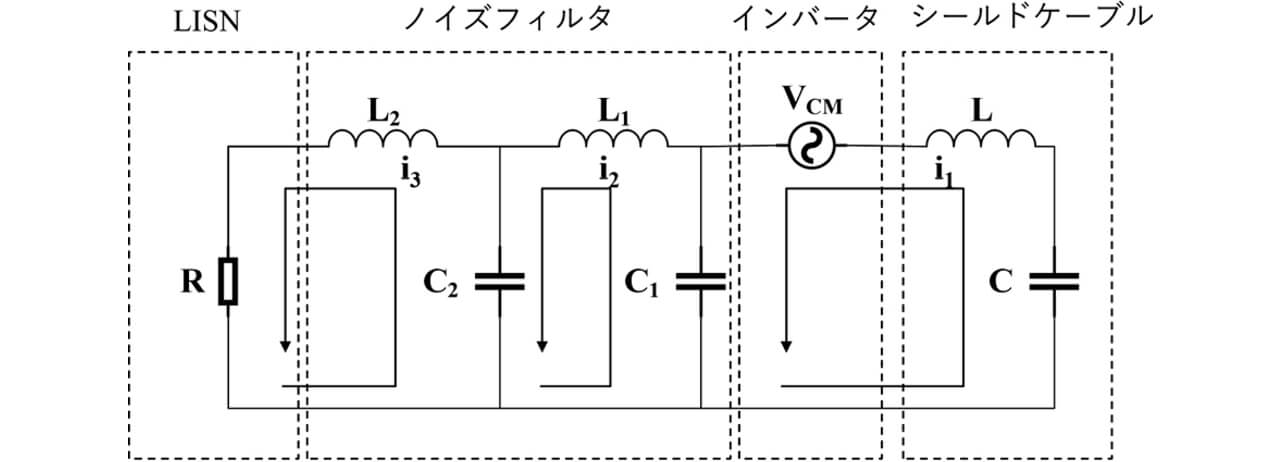
図8は、文献9)に示されたコモンモード等価回路にノイズフィルタを追加したものである。実際のコモンモード等価回路は、配線や素子の寄生インピーダンスを模擬する必要があるが、理論解析の簡易化のため主要なコモンモード成分のみを考慮した 。雑音端子電圧の低周波数帯域(150 kHz~300 kHz程度)においては、寄生インピーダンスの影響が小さいため、図8の等価回路が適用できると考えられる。一方で、より高周波帯域では、共振によるノイズ増幅が問題となるため、配線や素子の寄生インピーダンスを含めた解析が必要となる。
ここで、vCM はコモンモード電圧、i1~i3は各部を流れるコモンモード電流を表す。ノイズフィルタは2段のLCフィルタとし、L1とL2はコモンモードインダクタンス、C1とC2はコンデンサ容量を表す。シールドケーブルについては、ここではケーブル長固定とし、配線のインダクタンスをL、配線とシールド間の浮遊容量をC で表す。R をLISNの雑音端子電圧測定用の抵抗とすると、雑音端子電圧v は(2)式で表される。

よって、i3が求まれば雑音端子電圧の理論式が導出できる。図4のコモンモード等価回路のi1~i3についての閉路方程式は(3)式で表される。

(3)式中のVCn は、コモンモード電圧vCM をフーリエ級数で表したときの、スイッチング周波数を基本周波数とする高調波成分の実効値である。ここで、nは高調波の次数を表し、ωn はn次高調波の角周波数を表す。(3)式において、ノイズフィルタの回路定数をL1 = L2 = 7 mH、C1 = 0.11 μF、C2 = 0.05 μFとすると、f = 150 kHzのとき、ωL1 = ωL2 = 1050Ωに対し、1/jωC1 = 9.6Ω、1/jωC2 = 21Ωとなる。このとき、ωL1 ≫ 1/jωC1、ωL2 ≫ 1/jωC2より、i1 ≫ i2、i2 ≫ i3となるので、(3)式は(4)式で近似できる。

(4)式をi3について解けば、(2)式より雑音端子電圧が求まる。n次高調波の雑音端子電圧Vn は(5)式となる。

(5)式において、ケーブル長および軸数が影響するのは、右辺の第1項のみである。ここで、シールドケーブルのケーブル長をl、軸数をN、単位長さ当たりの浮遊容量をCS 、単位長さ当たりの配線インダクタンスをLS とする。ここで、並列接続されたすべての軸の動作条件、およびケーブル長が同一であると仮定すると、(5)式中のCはNCSl、LはLSl /N で置き換えられる9)。(5)式右辺第1項より、雑音端子電圧は(6)式で表されるVn (l, N )に比例する。

(6)式から、1軸のサーボドライブシステムにおいてケーブル長がl1からl2に変化したときの、雑音端子電圧の変化量は(7)式で表される。

同様に(6)式から、サーボドライブシステムの軸数が1軸からN軸に変化したときの、雑音端子電圧の変化量は(8)式で表される。

(7)(8)式の右辺に着目すると、右辺分母の第2項にもシールドケーブルの長さと軸数のパラメータが含まれる。このことから、ノイズフィルタのコンデンサ容量C1に対して、浮遊容量が無視できない程度に大きくなる場合、雑音端子電圧はケーブル長や軸数に比例しなくなることが分かる。
次に、伝導ノイズシミュレーションにおけるシールドケーブルのケーブル長と軸数に対する雑音端子電圧の変化について理論式と比較を行う。図9に、伝導ノイズシミュレーションにおけるシールドケーブルとモータモデルを示す。
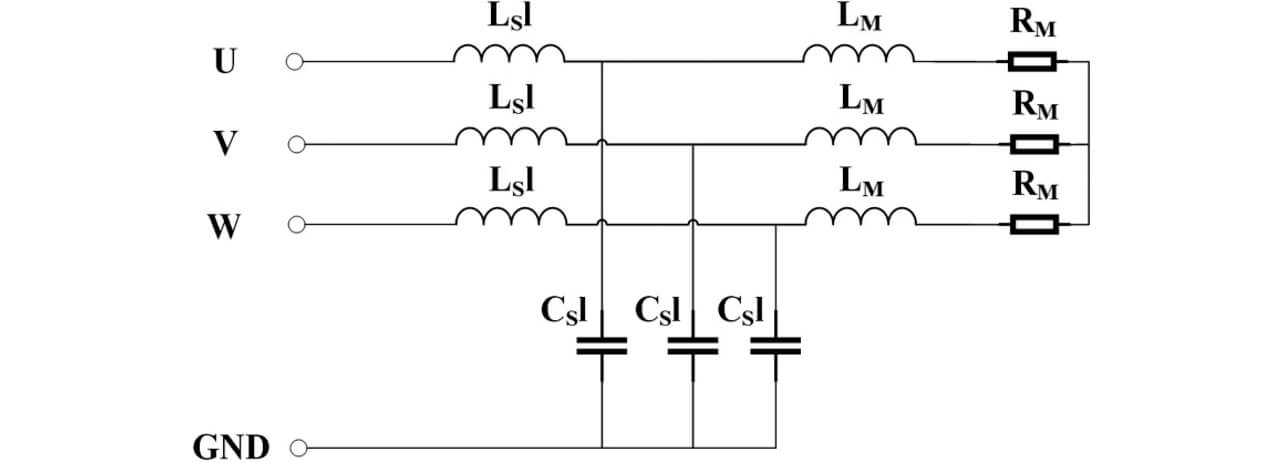
図9において、LM とRM はそれぞれモータの巻線インダクタンスと巻線抵抗を示している。本検討においては、シールドケーブルからの高周波漏れ電流に着目するため、モータとGND間の浮遊容量は考慮していない。
図10、図11にそれぞれケーブル長および軸数を変化させたときの雑音端子電圧(152 kHz)について、理論値と図3のモデルによるシミュレーション値の比較結果を示す。
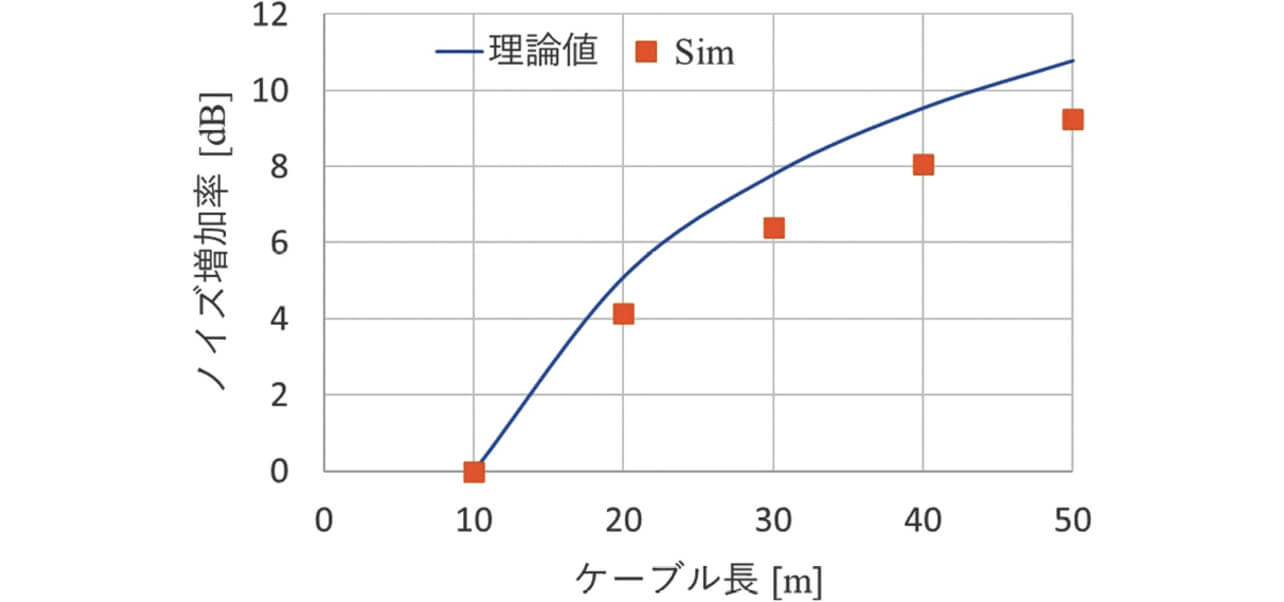
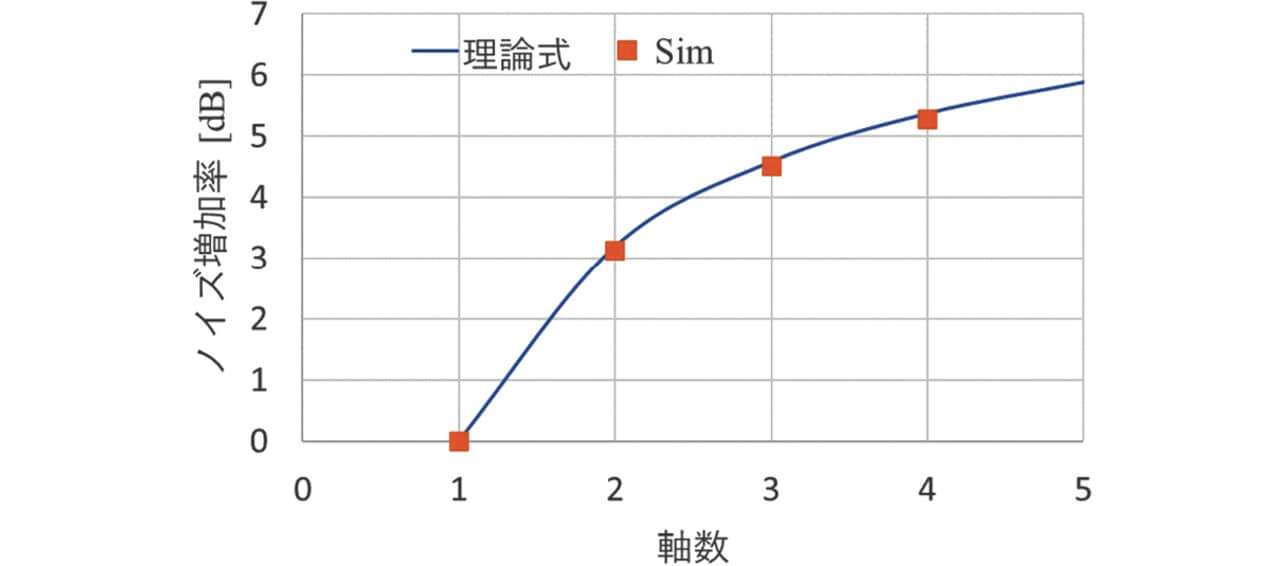
ここで152 kHzは、コモンモード電圧の19次高調波に対応し、雑音端子電圧で対象とする周波数帯における最小奇数次数である。図10は、1軸のサーボドライブシステムにおいて、ケーブル長10 mを基準として、ケーブル長を変化させたときの雑音端子電圧増加率の理論値とシミュレーション値を示している。図11は、ケーブル長を50 m固定として、ノイズフィルタに接続するサーボドライブの軸数を1軸から変化させたときの雑音端子電圧増加率の理論値とシミュレーション値を示している。図10、図11から、ケーブル長および軸数に対する雑音端子電圧増加率は、理論値とシミュレーション値ともに比例しておらず、伝導ノイズシミュレーションはノイズ増減傾向を再現できているといえる。また、図11から、軸数に対する雑音端子電圧増加率は、理論値とシミュレーション値で良く一致していることがわかる。一方で、図10において、基準ケーブル長を10 mとしたときの、ケーブル長に対する雑音端子電圧の増加率は、理論値とシミュレーションで誤差が生じている。これは、理論式では主要なコモンモード成分のみを考慮したが、シミュレーションでは基板・素子の寄生成分も考慮しているためと考えられる。
この結果から、ケーブル長に対する雑音端子電圧の変化をより正確に予測するためには、素子や基板などの寄生インピーダンスを含めた解析が必要であることがわかる。
3.4 ケーブル長に対する周波数特性の再現
インバータの出力配線にシールドケーブルが適用された場合、ケーブルの寄生インピーダンスによりコモンモードの共振が生じることが報告されている7)。ケーブルの寄生インピーダンスによる共振は、特定の周波数(共振周波数)で高周波漏れ電流を増幅するため、高周波漏れ電流が系統や他機器へ与える影響を評価する上で、その周波数特性を再現することが重要である。図12に、ケーブルの寄生インピーダンスによるコモンモード共振を解析するためのコモンモード等価回路を示す。
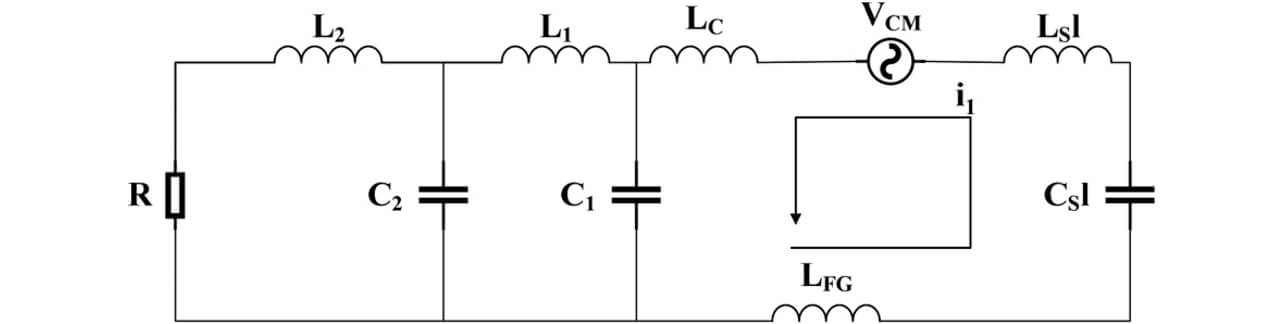
図12は、図8のコモンモード等価回路に、LC とLFG を追加したものである。図12において、LC は基板および配線のインダクタンス、LFG はGNDのインダクタンスを表す。また、シールドケーブルの長さをl、単位長さ当たりの浮遊容量をCS 、単位長さ当たりの配線インダクタンスをLS とする。ケーブルの寄生インピーダンスによるコモンモード共振は、図12中のコモンモード電流i1のループにおけるLC直列共振である。よって、共振周波数fr の理論式は(9)式で近似される。

共振周波数とはノイズの周波数特性におけるピーク値のことである。(9)式において、C1、CS 、LS 、l は設計値であり既知のパラメータである。また、LC は基板および配線構造から簡易計算により算出可能である。よって、LFG が未知のパラメータとなる。LFG は、シールドケーブルのシールドと接地線のインダクタンスの和となる。ここで、接地線はノイズフィルタとサーボドライブ間の配線が支配的であり、インダクタンスは既知である。シールドの単位長さ当たりのインダクタンスは未知であるが、シールドケーブルの構造から単位長さ当たりの配線インダクタンスの1/2で近似した。(10)式にLFG の近似式を示す。

Lg :接地線の配線インダクタンス
図13に、図3の伝導ノイズシミュレーションにおいてケーブル長を変化させたときに雑音端子電圧に生じる共振周波数と、理論式の比較結果を示す。
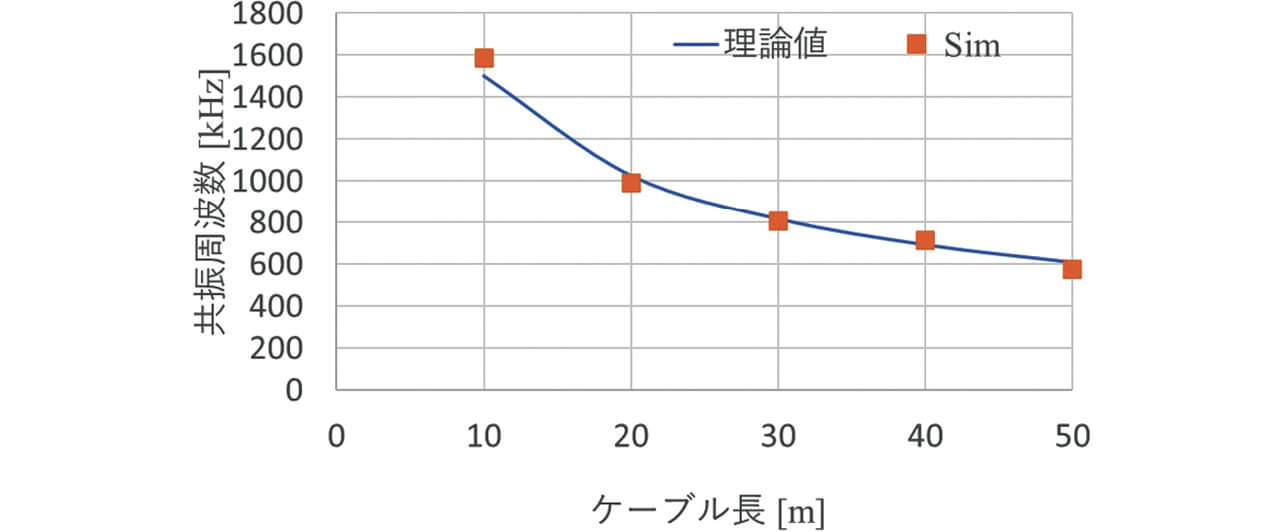
図13から、シミュレーションの共振周波数は、理論値と良く一致していることがわかる。伝導ノイズシミュレーションにより共振周波数を評価できれば、ノイズのメカニズム分析に有効であり、対策検討の一助となる。
4. 解析手法の評価結果
4.1 ケーブル長に対するノイズ増減の評価結果
サーボドライブAC給電システムの雑音端子電圧の測定結果との比較により、伝導ノイズシミュレーションの妥当性評価を行った。表2に、評価対象のサーボドライブAC給電システムの主要パラメータを示す。
| 項目 | パラメータ |
|---|---|
| 電源入力 | 3 Φ AC 240 V/50 Hz |
| 出力電力 | 100 W |
| ノイズフィルタ | FSB-30-254-HU(コーセル社) |
| 整流回路 | ダイオード整流 |
| 平滑回路 | 電解コンデンサ |
| キャリア周波数 | 16 kHz |
| 動力ケーブル | シールドケーブル C: 460 pF/m L: 21 nH/m |
表2において、シールドケーブルの単位長さ当たりの容量CとインダクタンスLは実験で使用したケーブルのメーカによる測定値である。図14に、1軸のサーボドライブAC給電システムのケーブル長を変化させたときの雑音端子電圧測定結果を示す。
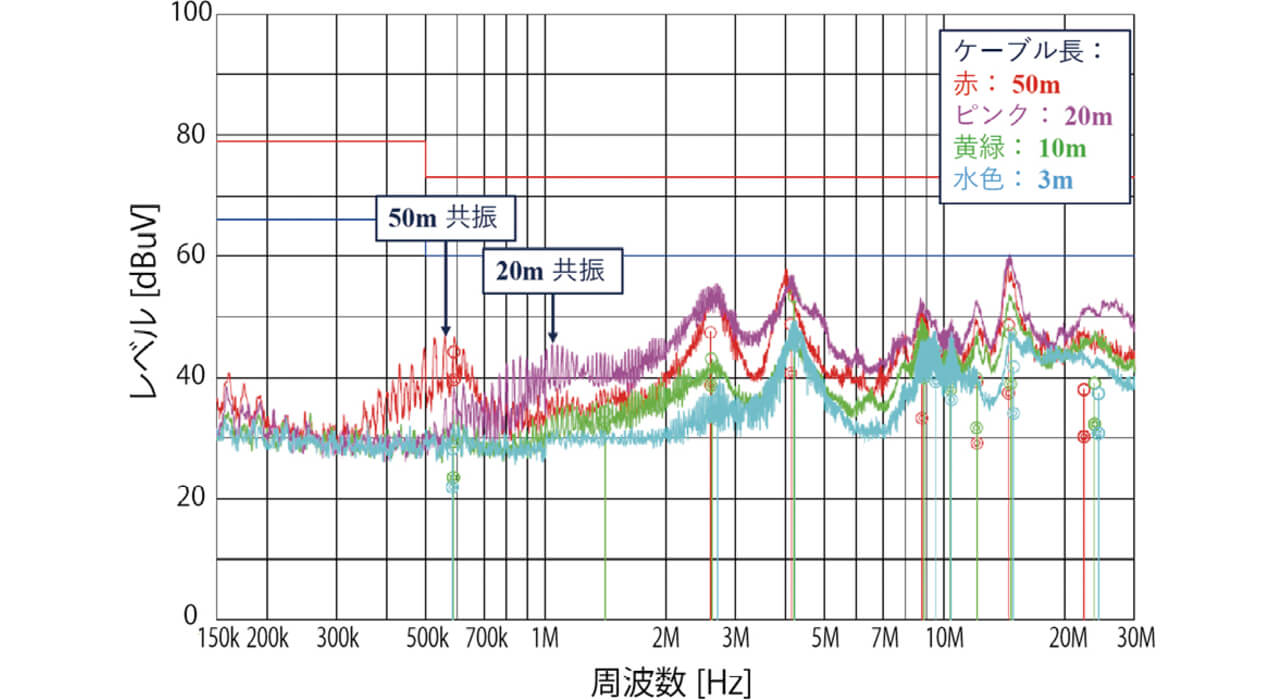
本検討では、シールドケーブルからの高周波漏れ電流の影響について評価するため、図14において、シールドケーブルの浮遊容量が支配的と考えられるケーブル長10、20、50 mについて評価した。図15に、ケーブル長10 mを基準としたケーブル長に対する雑音端子電圧(176 kHz)について、測定値とシミュレーションの比較結果を示す。
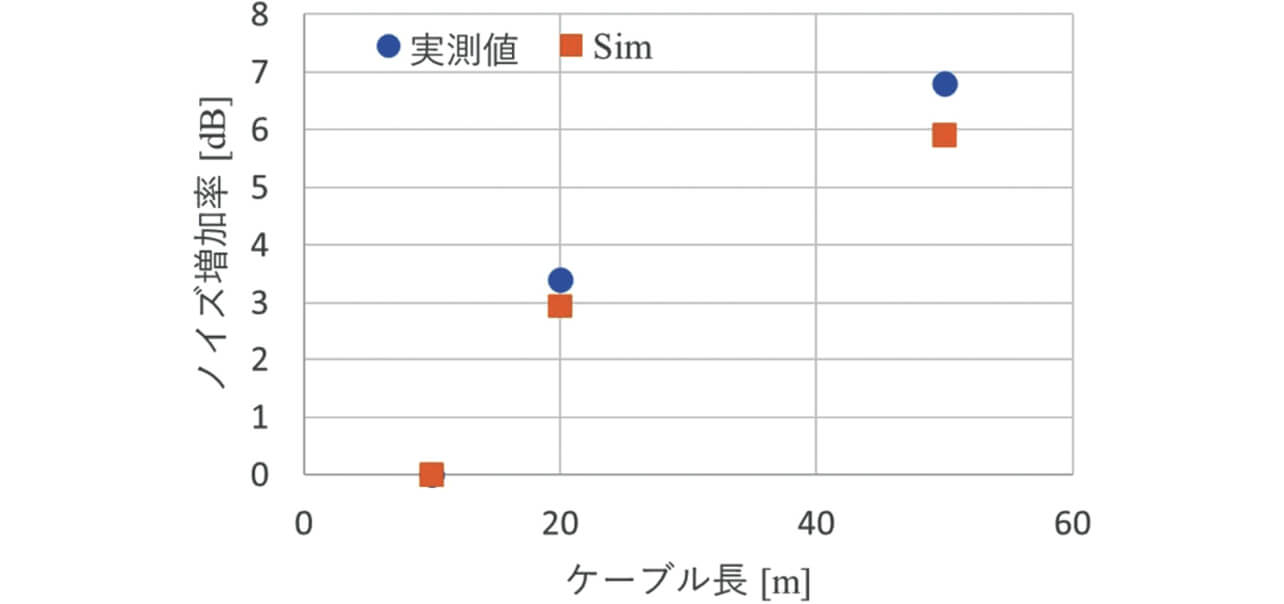
図15から、ケーブル長に対する雑音端子電圧増加率は、測定値とシミュレーションで誤差は≦1 dBであり、良く一致していることがわかる。この結果から、伝導ノイズシミュレーションは、ケーブル長によるノイズ増減を再現できているといえる。
4.2 ケーブル軸数に対するノイズ増減の評価結果
次に、ノイズフィルタに並列接続するサーボドライブシステムの軸数を変化させた場合の、測定値とシミュレーション値の比較を行った。図16に、1軸および3軸のサーボドライブAC給電システムの雑音端子電圧測定結果を示す。
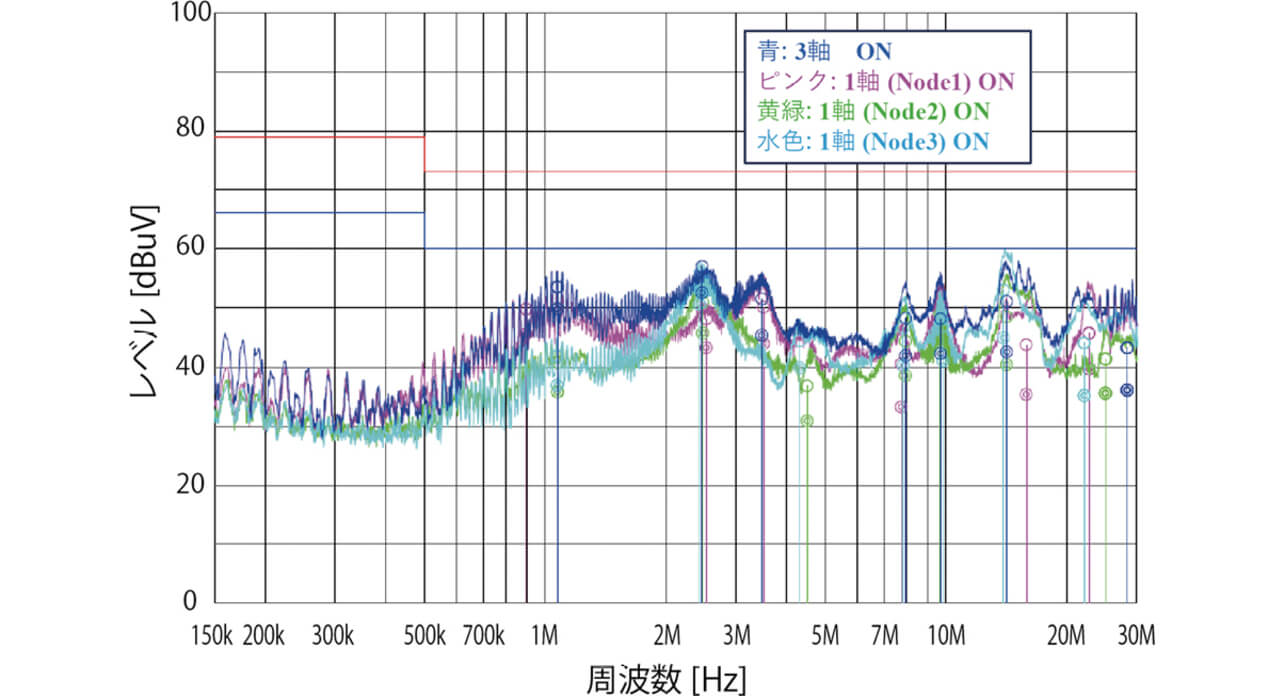
図16は、ケーブル長を20 mで固定し、3軸のサーボドライブを1軸ずつ動作させたとき、および3軸同時に動作させたときの雑音端子電圧の測定値である。図16から、1軸に対する3軸の雑音端子電圧(176 kHz)の増加率は、7.3 dBである。これに対し、シミュレーション結果は6.6 dBであり、測定値とシミュレーション値は一致しているといえる。この結果から、伝導ノイズシミュレーションは軸数によるノイズ増減を再現できているといえる。
4.3 ケーブル長に対する周波数特性の評価結果
図17に、ケーブル長を変化させたときに雑音端子電圧に生じる共振周波数について、図14の雑音端子電圧(1軸)における測定値とシミュレーションの比較結果を示す。
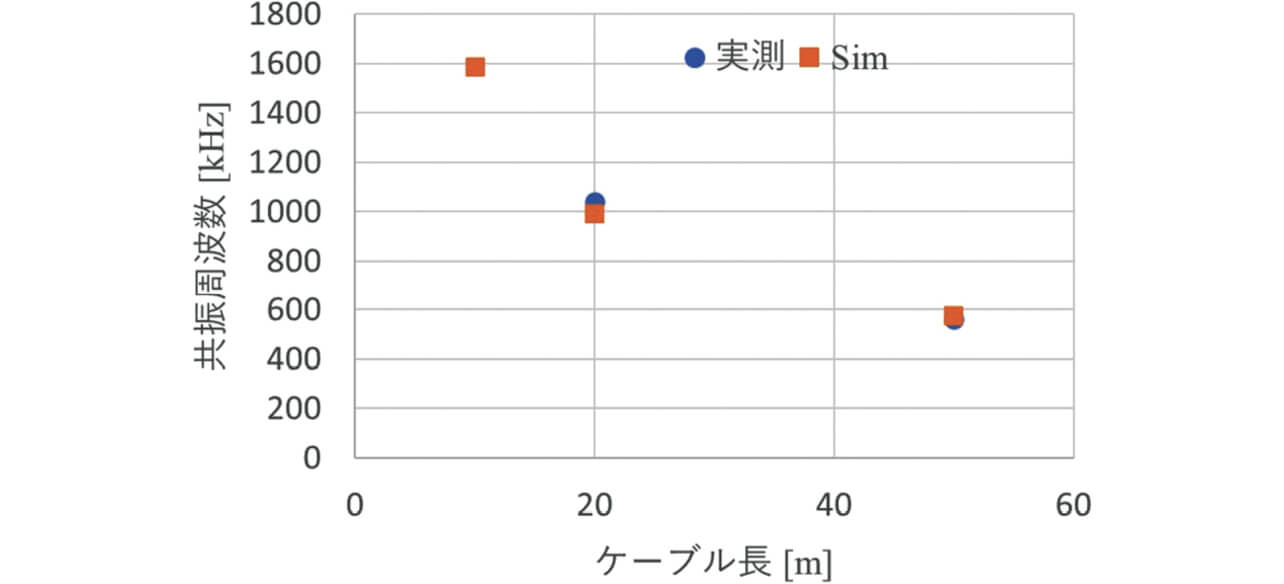
測定結果において、ケーブル長10 mでは明確な共振のピークが確認できなかったため、測定値はケーブル長20 mと50 mの結果のみを示している。図17から、シミュレーションの共振周波数は、測定値と良く一致していることがわかる。この結果から、伝導ノイズシミュレーションは、ケーブル長に対する雑音端子電圧の周波数特性を再現できているといえる。
5. むすび
本論文では、サーボドライブの開発期間短縮を目的として、シールドケーブルからの高周波漏れ電流が系統や他機器へ与える影響を評価可能な伝導ノイズ解析手法を検討した。基板・ノイズフィルタの寄生成分およびGNDのインピーダンスを正確にモデル化することで、伝導ノイズシミュレーションにより、シールドケーブルの長さや軸数に対するノイズの増減や周波数特性を再現できることを示した。結果として、既存のサーボドライブAC給電システムに対して、シールドケーブルのケーブル長・軸数を変化したときの雑音端子電圧の変化傾向を再現した。本技術により、開発上流工程でのノイズ対策と設計反映が可能となり、サーボドライブ商品の開発期間短縮に寄与できると考える。
今後は、本技術を多軸のサーボドライブDC給電システムに適用し、シールドケーブルからの高周波漏れ電流によるノイズ課題を事前抽出、検証することで、伝導ノイズ解析手法の効果を検証していく。
参考文献
- 1)
- 環境省.“産業部門(製造業)の指針(対策メニュー)”.温室効果ガス排出削減等指針.https://www.env.go.jp/earth/ondanka/gel/ghg-guideline/industry/measures/view/86.html, (2023.1.10).
- 2)
- Yoshikawa, H. “Energy Saving System Trend for Harbor Crane with Lithium Ion Battery”. The 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCA Asia). 2018, p.219–226.
- 3)
- 桐淵岳,財津俊行,土井昌志,日下佳祐,伊東淳一.サーボドライブDC給電システムのインピーダンス法による安定性解析.電学論D.2020, Vol.140, No.3, p.184-193.
- 4)
- 小笠原悟,藤田英明,赤木泰文.電圧形PWMインバータが発生する高周波漏れ電流のモデリングと理論解析.電学論D.1995, Vol.115, No.1, p.77-83.
- 5)
- 玉手道雄,佐々木達未子,鳥羽章夫.インバータにおける雑音端子電圧のシミュレーションによる定量推定法.電学論D.2008, Vol.128, No.3, p.193-200.
- 6)
- 嶺岸瞳,崎山一幸,山田徹.インバータ電源回路のコモンモードノイズ解析手法の検討.信学技報.2012, Vol.112, No.100, EMCJ2012-23, p.14-16.
- 7)
- 埴岡翔太,家澤雅宏,小笠原悟司,竹本真紹,折川幸司.2モータ駆動システムのコモンモードノイズ抑制制御.電学論D.2021, Vol.141, No.11, p.895-902.
- 8)
- 土田崇.インバータ出力配線へのシールドケーブルの適用に関する検討.電学論D.2012, Vol.132, No.7, p.718-726.
- 9)
- 和田圭二,石塚哲也,清水敏久.ACモジュール方式系統連系インバータシステムの伝導ノイズとその抑制法.電学論D.2005, Vol.125, No.10, p.911-918.
- 10)
- 玉手道雄,鳥羽章夫,松本康,和田圭二,清水敏久.複数の電力変換装置から構成されるシステムにおける雑音端子電圧低減に適したキャリア位相制御法.電学論D.2011, Vol.131, No.6, p.811-819.
PSIMは、米国Altair Engineering, Inc.の米国およびその他の国における登録商標または商標です。
本文に掲載の名称は、各社が商標としている場合があります。














