伝送線路からの不要な放射の抑制によるミリ波レーダの方位推定精度の向上
非接触でヒトやモノの位置などをセンシングする手段としてミリ波レーダが注目されており、車載や交通インフラ、ファクトリーオートメーション(FA)、ヘルスケアなど幅広い領域での活用が期待されている。レーダがターゲットの位置を正しく検出するためには、電波が到来した方位を高い精度で推定することが必要である。レーダの構成部位のうち、伝送線路など、アンテナ以外の部位から電波が放射されると、電波の到来方位の推定精度が低下する。そこで、これまで基板の表面に形成していた伝送線路に替えて、基板の内層を電磁界が伝搬する構造である基板集積伝送線路(SIW)を導入することで、不要放射を抑制して電波の到来方位の精度を向上させることを検討した。本稿では、電磁界シミュレーションを用いて不要な放射が抑制される効果を示すともに、ビームフォーマ法に基づく到来方位推定における誤差が従来の4.1°から1.2°へ向上することを述べ、SIWの導入がより高い精度でターゲットの位置を検出するミリ波レーダの実現に有効であることを明らかにする。
1. まえがき
近年、非接触でヒトやモノを検出する手段としてレーダ技術の活用が検討されている。レーダは、逆光や暗闇、霧など環境の状態の影響を受けずにターゲットの位置や速度を検出できるほか、センシングにあたってプライバシーを確保しやすいなどの特徴を備える。とりわけミリ波を使用するレーダ(以下「ミリ波レーダ」)は、使用する波長が数ミリメートル程度と従来広く用いられてきたレーダに比べて短いことや使用できる周波数帯域幅が広いことから、高い空間分解能を得ることができる。また、半導体製造技術の進化に伴うミリ波ICの低廉化や、法改正によるミリ波帯の規制緩和に伴い、ミリ波レーダを利用しやすい環境が整いつつある。このような状況を受け、ミリ波レーダは自動車やモバイルロボット(AMR)の自動運転の実現に向けた障害物検出や、歩行者を含めた交通状況の監視1)、住宅や施設内における人物の健康状態把握など幅広い分野2)3)で活用が広まっていくことが期待されている。
ミリ波レーダをこうした用途で活用するためには、ターゲットの位置を高い精度で検出することが求められる。例として、交差点の近傍に設置したミリ波レーダで交通状況を監視し、検出した結果を周囲の車両に通知することで交通事故の防止を図るシステムが挙げられる。このシステムにおいては、数メートルないし十数メートル離れた人物や車両の位置を正確に検出する必要がある。このとき、ターゲットの位置を誤ると、例えば実際には安全な歩道上に歩行者が存在するにもかかわらず、交差点内の危険な位置に存在すると誤認して、円滑な交通を阻害する可能性がある。また、健康状態を把握するシステムでは、複数の人物が近接して存在するとき、位置の検出精度が低いと、正しくバイタル信号を検出できない可能性がある。例として、保育施設において乳幼児が午睡をとるときに健康状態に変化がないか見守る用途を考える。このような用途では、天井や壁に設置したレーダで、互いに近接して寝ている複数の乳幼児のバイタル信号を同時に検出するシーンが想定される。このとき、位置の検出精度が低いと、ある人物が誤った位置に検出され、別の人物の検出位置と重なるおそれがある。すなわち、レーダが受信した信号を位置ごとの信号に分解して、人物を検出した位置の信号からバイタル信号を取り出すとき、複数の人物の検出位置が重なると、それらのバイタル信号が重畳して、正しくバイタル信号を検出できないことが懸念される。
ミリ波レーダで位置を正しく把握するためには、電波の到来方位を高い精度で検出することが必要となる。そのためには、アンテナ以外の構成要素から電波を放射しないことが求められる。レーダの構成要素のうち、不要な電波を放射しうるものとして伝送線路が挙げられる。すなわち、ミリ波レーダではアンテナを物理的に回転させることなく電波の到来方位を推定するために、複数のアンテナを並べて配置したアレーアンテナが広く用いられており、空間的に離れた複数のアンテナを1つのミリ波ICに接続するため、アンテナとミリ波ICとの間に、ある程度の長さの伝送線路を配置する必要がある。より具体的には、小型のミリ波レーダにおいては、設計の容易化のため、プリント基板上にアンテナおよび伝送線路、ミリ波ICが配置されることが多い。プリント基板で多用される伝送線路として、マイクロストリップ線路(MSL)やグランド(GND)付きコプレーナ線路(GCPW)が挙げられる。MSLやGCPWは伝送損失が比較的小さい一方で、信号線が空間に露出し電磁界が空間に放射されやすい構造であるため、到来方位の推定精度が低下することが懸念される。
空中への電波の放射が比較的小さい伝送線路として、両面にGNDを形成した基板の内層に電磁波を伝搬させる構造である基板集積導波路(SIW)が挙げられる。基板に形成するアンテナとして多用されるマイクロストリップアンテナ(MSA)にSIWを用いて給電する構成の設計例はこれまでにも報告されている4)-6)。ただし、これらの報告は伝送線路から放射される電力がレーダの到来方位推定精度に与える影響について言及していない。いっぽうで、実際にSIWをレーダに適用すべきか判断するうえでは、SIWを導入することによる到来方位推定精度の具体的な改善効果を明らかにする必要がある。そこで本稿では、MSAへの給電線路としてSIWを導入することによる到来方位推定精度の改善効果を電磁界シミュレーションを用いて定量的に明らかにする。また、この過程で用いる到来方位推定精度の評価指標が定まっていなかった。そこで、真の到来方位をある角度区間内で掃引したときの推定誤差の最悪値で評価する方法を導入して効果を得たのでその内容を報告する。
まず2章でSIWやMSL、GCPWの特性を比較し、3章にて、ミリ波レーダを構成する伝送線路にSIWを導入することで伝送線路からの放射が抑制されることを電磁界シミュレーションを用いて示す。さらに4章にて、電磁界シミュレーションの結果として得られた放射パターンに到来方位推定アルゴリズムを適用して、到来方位の推定精度が向上することを述べる。
2. 伝送線路の特性
2.1 SIWの設計
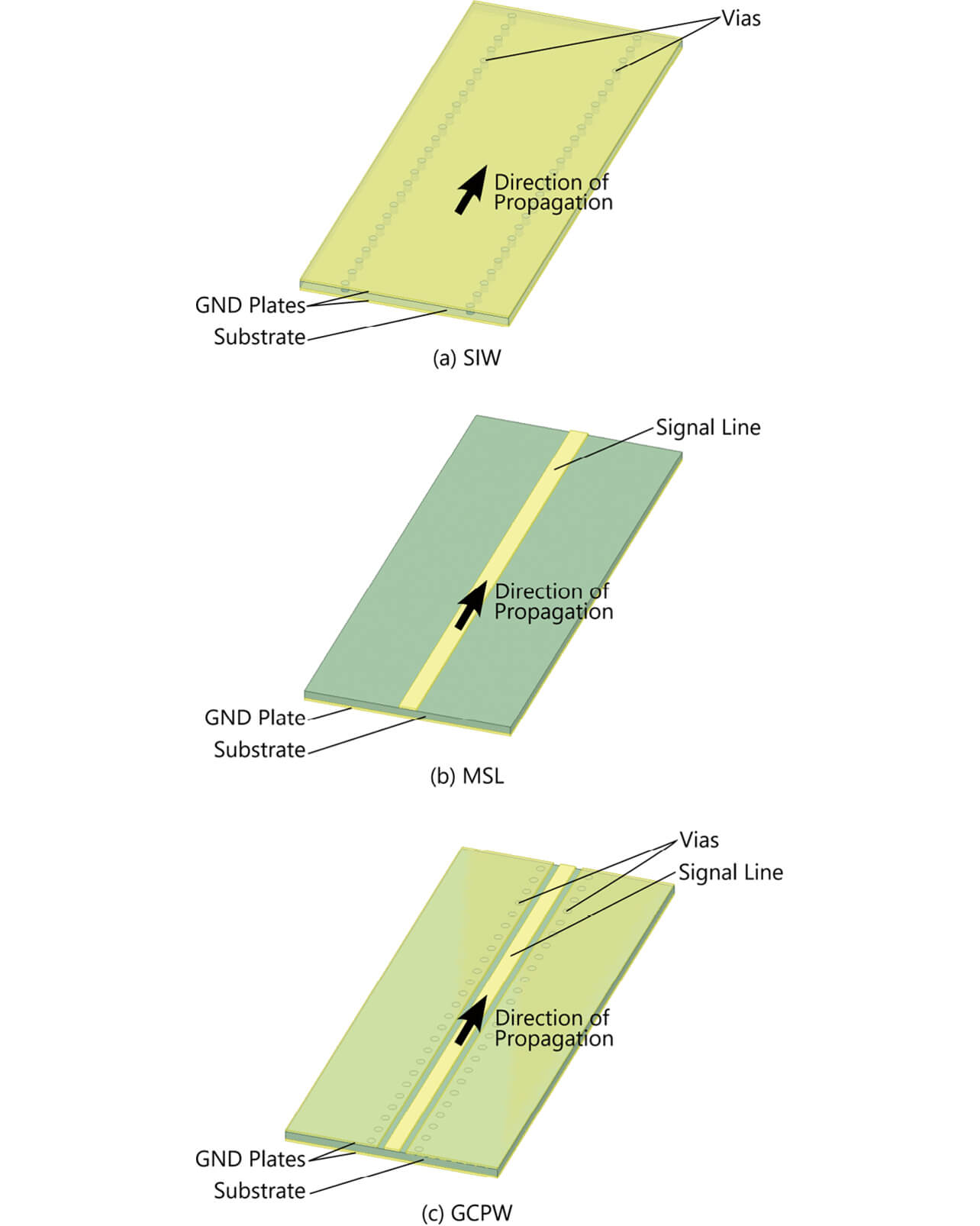
1章で述べたように基板に形成するミリ波伝送線路のうち代表的なものとして、SIWやMSL、GCPWが挙げられる。このうちSIWは図1(a)のように両面をGNDとした基板に、平行なビア列を形成し、ビア列の間に電磁波を伝搬させる伝送線路である。図1(b)および(c)に示すMSLやGCPWと異なり、電磁界が基板の内部に閉じ込められることから、空間への放射が原理的にきわめて小さい。また、ビア同士の間隔が十分に密であるとき、金属で囲まれた領域の内部を電磁波が伝搬すると見なせることから、方形導波管の一種と言える。
ここで、レーダに使用する周波数帯である60 GHz~64 GHzの電磁波をSIWに伝搬させるための線路幅の要件を検討する。方形導波管の代表的特性として、モードごとの伝搬する最低周波数である遮断周波数が挙げられ、次の式で与えられる:

この式において、c0は真空中における光速、p およびq はモード番号、μr およびεr は導波管内媒質(すなわち基板の基材)の比透磁率および比誘電率、a およびb は導波管の寸法である。SIWにおいては、a は線路の幅、b は基板の厚さと考えることができる。例として、表1に示す基材を用いるならば、b = 0.152 mm、μr = 1.0、εr = 3.2 となる。
| 項目 | 値 | ||
|---|---|---|---|
| 物性値 | 比誘電率 | εr | 3.2 |
| 比透磁率 | μr | 1.0 | |
| 誘電正接 | tanδ | 0.004 | |
| 寸法値 | 基板の厚さ | b | 0.152 mm |
| 銅箔の厚さ | tc | 0.040 mm | |
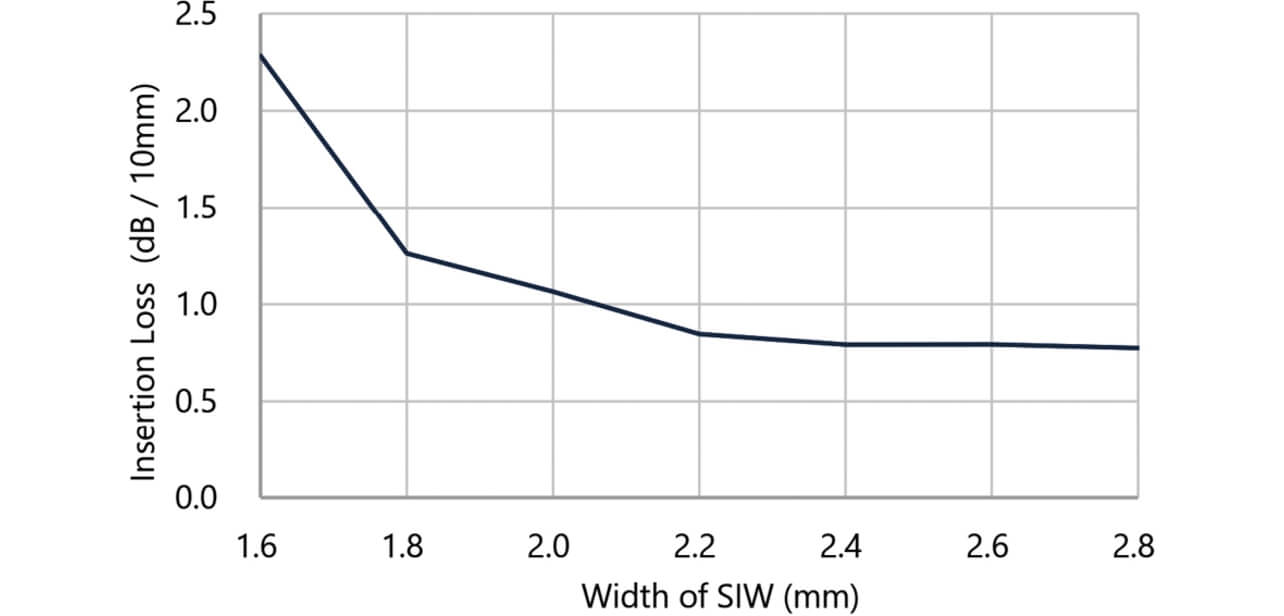
これらから、遮断周波数の最も低いTE10モードを伝送させるためには線路幅a は少なくとも1.6 mm以上とする必要があることがわかる。直線状のSIWについてa の値を変えながら挿入損失について電磁界シミュレーションを行ったところ、a を増すとa = 2.4 mm程度までは挿入損失が低減し、以降はほぼ一定値となる傾向が認められた(図2)。また、3章にて述べるように、a が大きいとレーダ基板に適用する際に生じる曲げ部の曲率半径が小さくなることから、曲げ部での損失が大きくなることが懸念される。これらを踏まえて、ここではa = 2.4 mmに設定した。
また、製造工程におけるクラックの発生を考慮してビア壁間の距離を0.25 mm以上と設計するようにした。したがってビアの直径を0.15 mmとするとき、ビアの間隔は0.4 mm以上とする必要がある。これを踏まえて、本検討ではシミュレーションモデルにおけるビア間隔を0.4 mmとした。線路幅やビアの設計値を表2に示す。
| SIW | MSL | GCPW | |
|---|---|---|---|
| 線路幅 | 2.400 mm | 0.370 mm | 0.330 mm |
| ビア直径 | 0.150 mm | ― | 0.150 mm |
| ビア間隔 | 0.400 mm | ― | 0.400 mm |
2.2 導波路の特性の比較
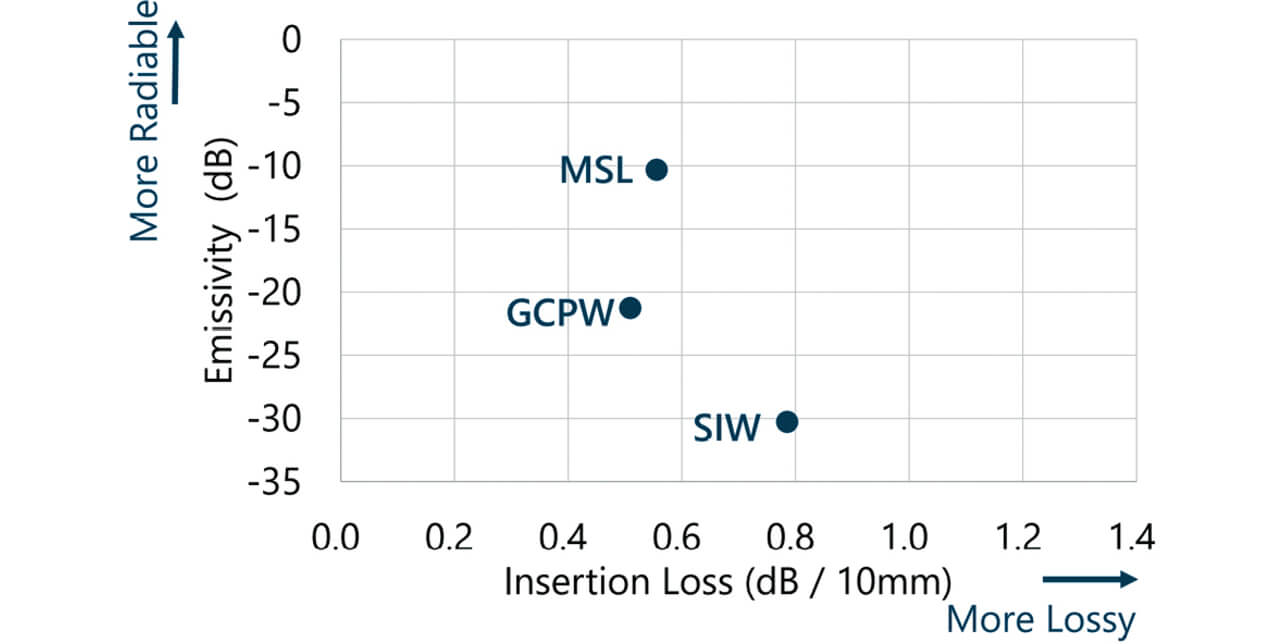
2.1節で設計したSIWと、信号線が空間に露出した構造であるMSL、GCPWについて、62 GHzにおける空間への放射率および挿入損失を比較する(図3)。ここで放射率は以下のように定義する。線路の両端にそれぞれポートを設置し、一方のポートから電力を供給する。ポートに入力した電力のうち一部は基板から放射され、解析空間の外へ放出される。ポートに供給した電力と解析空間の外へ放出される電力との比を放射率と定義する。
比較にあたっては、電磁界シミュレータAnsys HFSSを用いた。なお、GCPWおよびSIWは特性インピーダンスが50Ωとなるように設計した。具体的な設計値を先に示した表2に追記する。また、基板の長さ(伝送線路の長さ)を10 mm、基板の幅を4 mmとした。
まず図3の縦軸に示す放射率に着目する。想定したとおり、SIWから放射される電力はMSLやGCPWに比べて小さいことが確認された。これは電磁界が通過する領域を基板両面のGNDで挟み込む構造によって、電磁界の空間への漏れが抑制されたためと考えられる。
次に図3の横軸に示す挿入損失に着目する。SIWの挿入損失はMSLやGCPWに比べて大きい値となった。これは、MSLやGCPWでは電界の一部が空気中を通過するのに対して、SIWではほとんどの電界が基板の内部に閉じ込められることによって誘電損失が大きくなったためである可能性がある。
以上に述べたように、伝送線路から放射される電力を抑制するためにはSIWを選択することが望ましいことがわかる。これによって、挿入損失は増すものの、伝送線路からの放射電力がアンテナの放射パターンへ与える影響を低減する効果が見込める。
3. レーダ基板へのSIWの導入
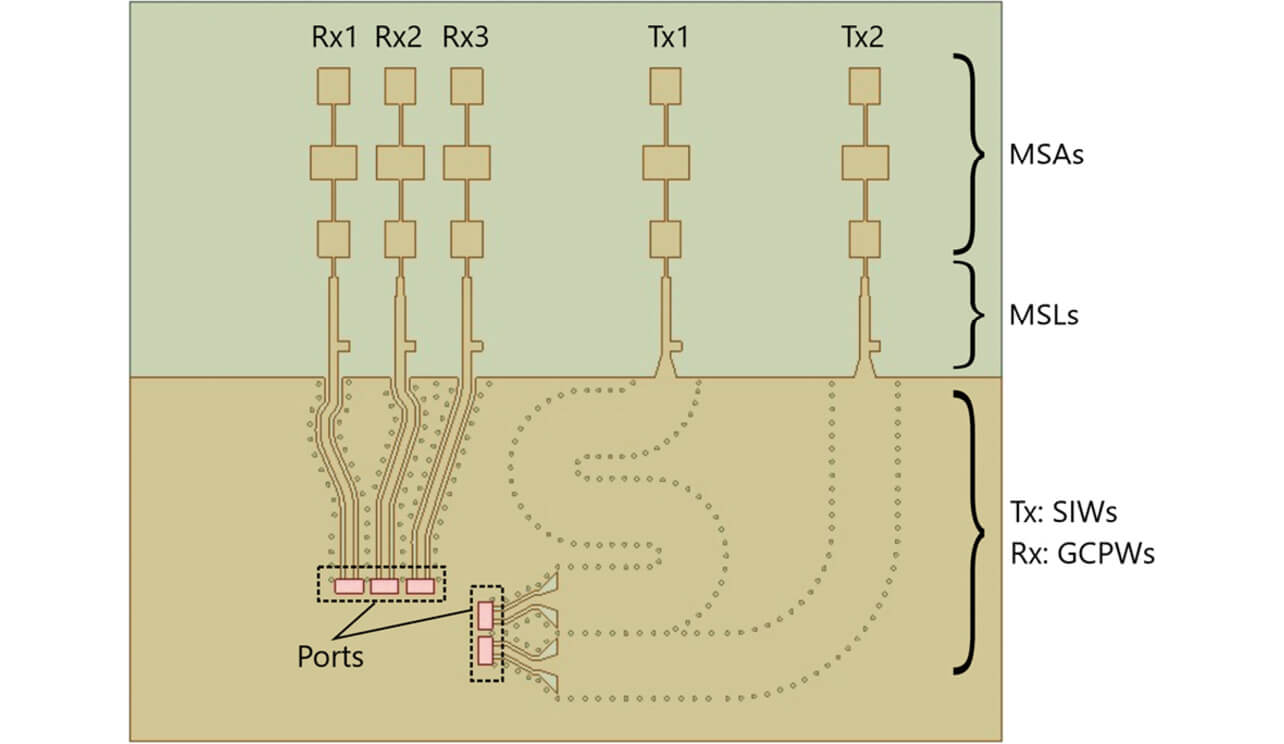
これまでに著者らが開発したレーダ基板の電磁界シミュレーションモデルを図4(a)に示す。XY面に平行な基板の表面に、2つの送信アンテナ(Tx1、Tx2)と3つの受信アンテナ(Rx1、Rx2、Rx3)を備え、YZ面内のビームを絞るためにそれぞれ3つのMSAをY方向に縦続し、MSLを利用したインピーダンス整合回路を介してGND端部に引き出す構成としている。GND端部からポート(図中の赤色矩形)までの区間はGCPWで配線されている。また、2つの送信アンテナへの伝送線路および、3つの受信アンテナへの伝送線路はそれぞれ等長となるように配線している。ここでは、表1に示す基材を使用した。また、受信アンテナ同士が近接していることから、相互結合の影響を低減することを意図して、Rx1およびRx3に隣接して寄生素子を配置した。以下ではこのモデルを「GCPWモデル」と呼び、伝送線路をSIWに置き換えたものとの比較検討を行う。
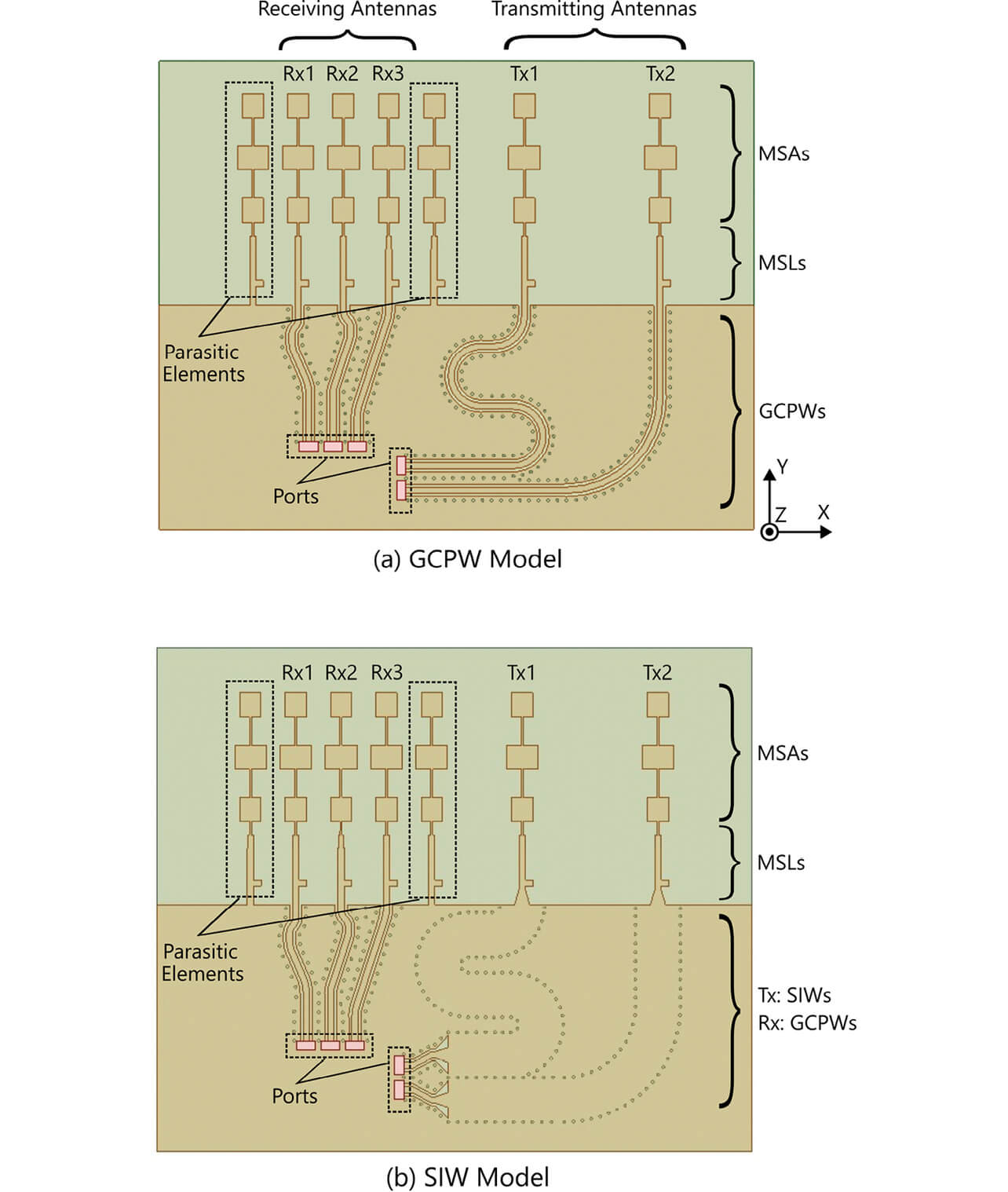
図4(b)に、ポートと送信アンテナとを結ぶGCPWをSIWに置き換えたモデル(以下「SIWモデル」)を示す。GND端部でMSLをSIWに接続し7)、ポートの近傍でSIWをGCPWに変換したうえで8)、ポートに接続した。すなわち、送信線路のうち従来GCPWで配線していた部分の大半をSIWに置き換えた。なお、先述したようにMSAと基板端部とを接続するMSLはインピーダンス整合に用いているため、SIWに置き換えずに残置した。
送信系統に属する2つの伝送線路を等長とする前提の下では、ポートとアンテナとの直線距離が短いTx1の伝送線路に複数の曲げ部を設ける必要がある。GCPWモデルの伝送線路を置き換える前提からポートとアンテナの位置が固定されていることを考慮すると、伝送線路の幅が広いほど曲げ部の曲率半径が小さくなる。曲げ部の曲率半径が小さくなると伝送損失が増大することが懸念される。そこで、2章での検討結果を踏まえて、SIWモデルにおけるSIWの幅を2.4 mmとした。
4. 到来方位推定精度の向上
4.1 放射パターン
GCPWモデルおよびSIWモデルについて、電磁界シミュレータHFSSを用いて、送信系統および受信系統の各アンテナの放射パターンを計算した。ここでポートから各アンテナに向けて入力する電圧の振幅および位相は同じ値とした。送信系統の62 GHzにおけるZX面内のY偏波放射パターンについて、振幅を図5に、位相を図6にそれぞれ示す。ここで、ZX面内における方位角は+Z方向を0°、+X方向を+90°と定義する。なお、受信系統については、GCPWモデルとSIWモデルとの間に構造的な違いがないことから放射パターンの図示を省略する。
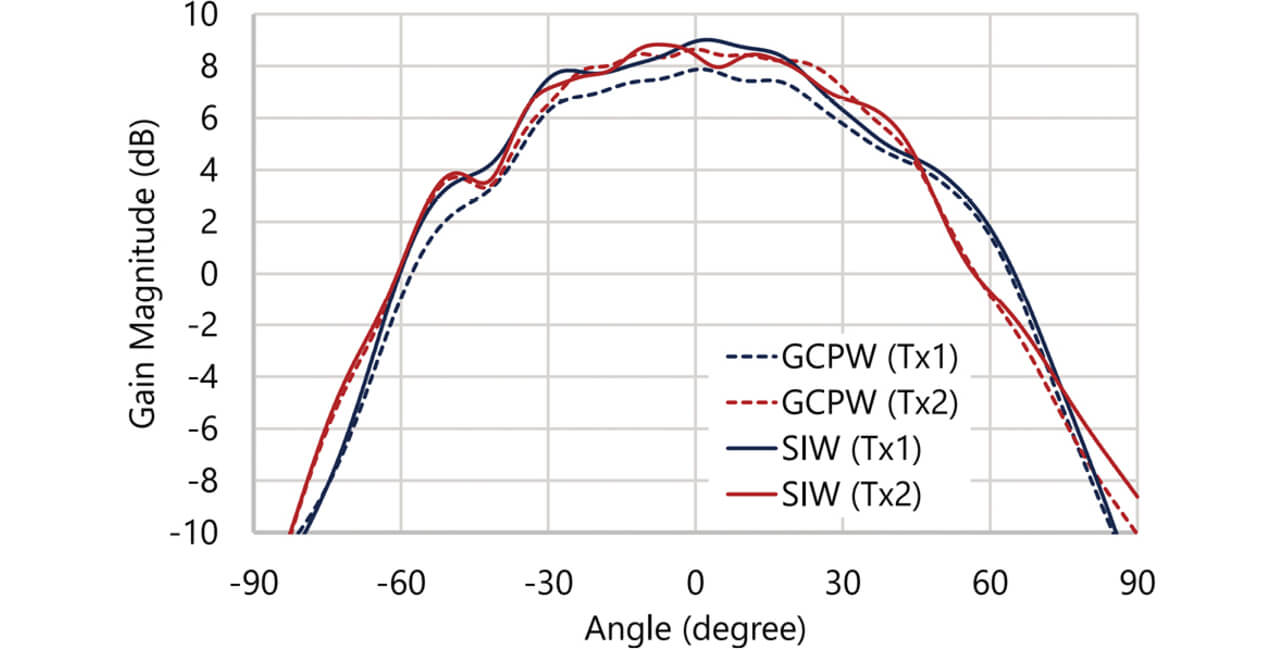
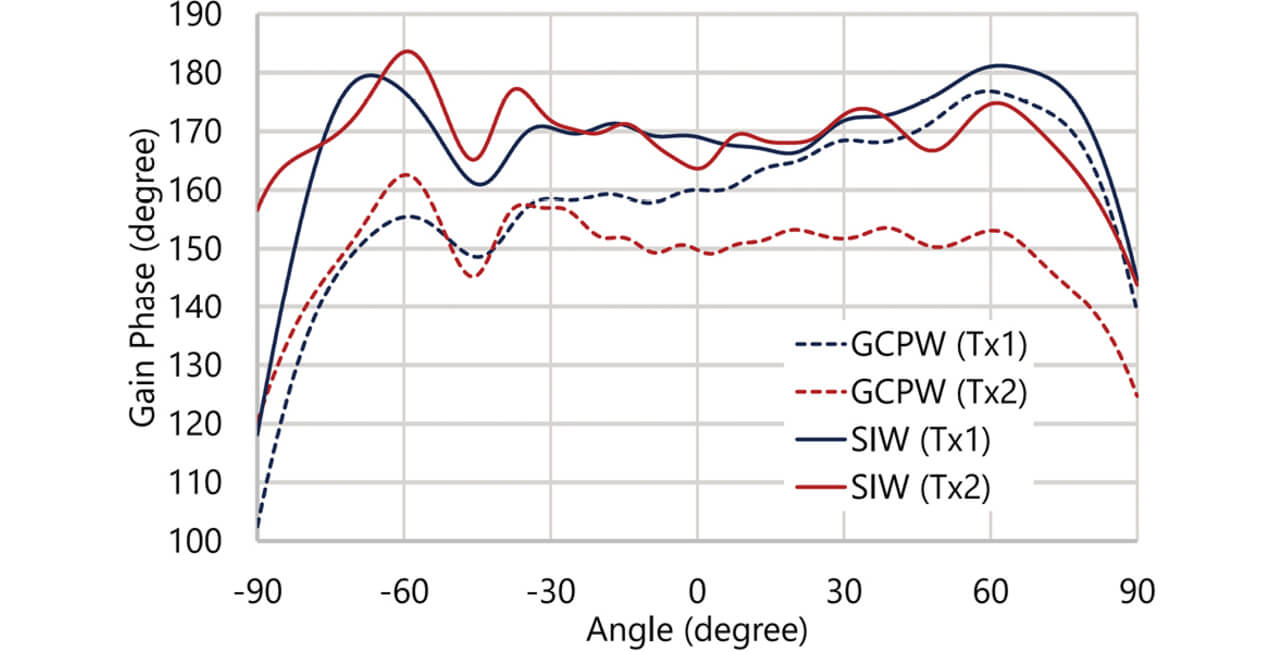
MSAはY軸に対して対称形であるから、アンテナ単体のZX面指向性は対称形であることが見込まれる。したがって、得られた指向性が対称形に近いほど伝送線路からの放射の影響が小さいといえる。図5および図6を参照すると、SIWモデルの方が対称形に近い。このことは、とくにTx1の位相パターンで顕著であるほか、Tx1の振幅パターンの ±45° や ±60°の近傍を比較してもわかる。したがって、伝送線路をSIWに置き換えることで、目論見通り伝送線路からの放射の影響を抑制できたといえる。
4.2 到来方位推定精度の算出方法
本節では到来方位推定精度の算出方法について述べる。ここでは、基板に設けた2つの送信アンテナと3つの受信アンテナの組み合わせにより、6チャネルのMIMOレーダを構成し、代表的な到来方位推定アルゴリズムであるビームフォーマ法を適用して到来方位を推定する。
ある方位θs から反射波を模した平面波が到来するとき、第m 送信アンテナと第n 受信アンテナからなるMIMOチャネルの受信信号xmn(θs )は

と表すことができる。ここで、Gm(θ)およびGn(θs )はそれぞれ第m 送信アンテナと第n 受信アンテナのθs 方向の利得(複素数)である。また、Δφmn はそれぞれの仮想アレーアンテナの相対位置によって生じる位相差、A は係数である。
方位θt に対する仮想アレーのモードベクトル D(θt )を用いると、θt 方向の信号強度 Po(θt )は

で与えられる。ここで [・]H は行列 [・] の随伴行列、
方位θt ごとにPo(θt )を計算することで、ビームフォーマ法に基づく方位スペクトラムが得られる。この方位スペクトラムが最大となる方位を検出方位θd とする。
以上の操作によって、真の到来波方位θs に対するレーダによる検出方位θd が求められた。したがって、検出誤差としてこれらの差
いっぽうで、「ある角度範囲の到来方位推定精度」を評価する指標がこれまで定まっていなかった。そこで、「ある角度範囲の到来方位推定精度」を「その角度範囲で保証される角度精度」と定義すると、「その角度範囲での最悪値(最大の検出誤差)」と言い換えることができる。すなわち、角度範囲




と書ける。本稿ではこの値を用いて到来方位推定精度を評価する。
4.3 到来方位推定精度向上の検証
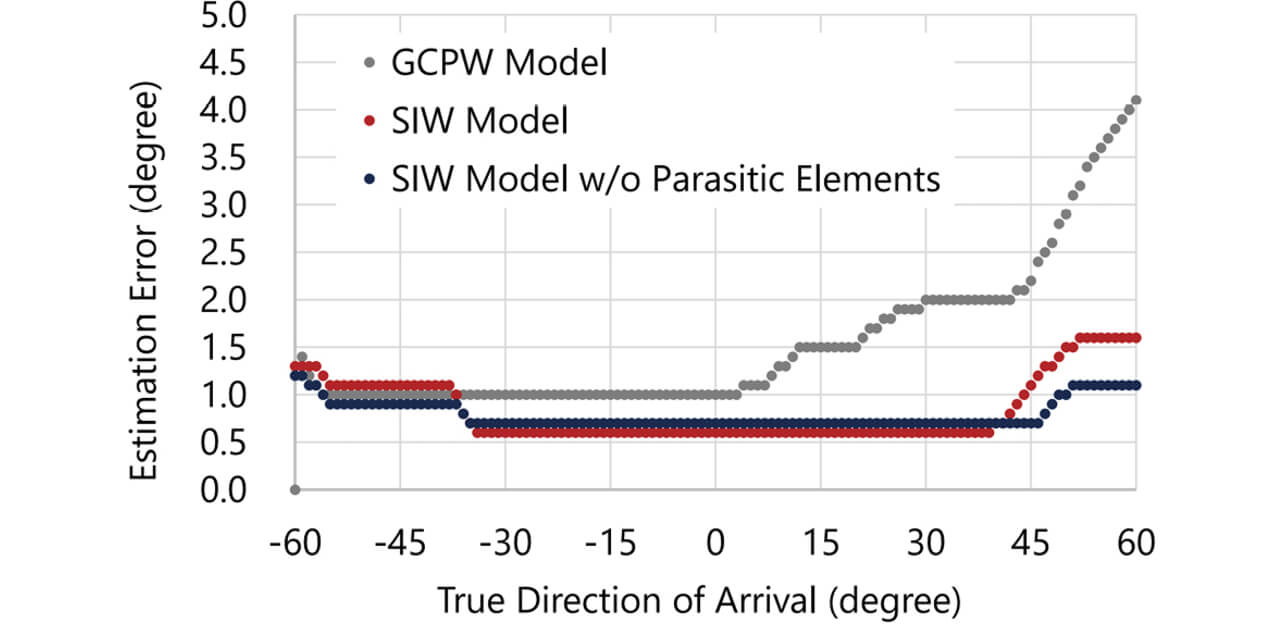
GCPWモデルとSIWモデルについて、利得パターンの電磁界シミュレーション結果に基づいて計算した到来方位推定精度を図7に示す。横軸の方位θx に対する縦軸は、真の到来波方位θs を0°からθx まで掃引した時の誤差の最大値
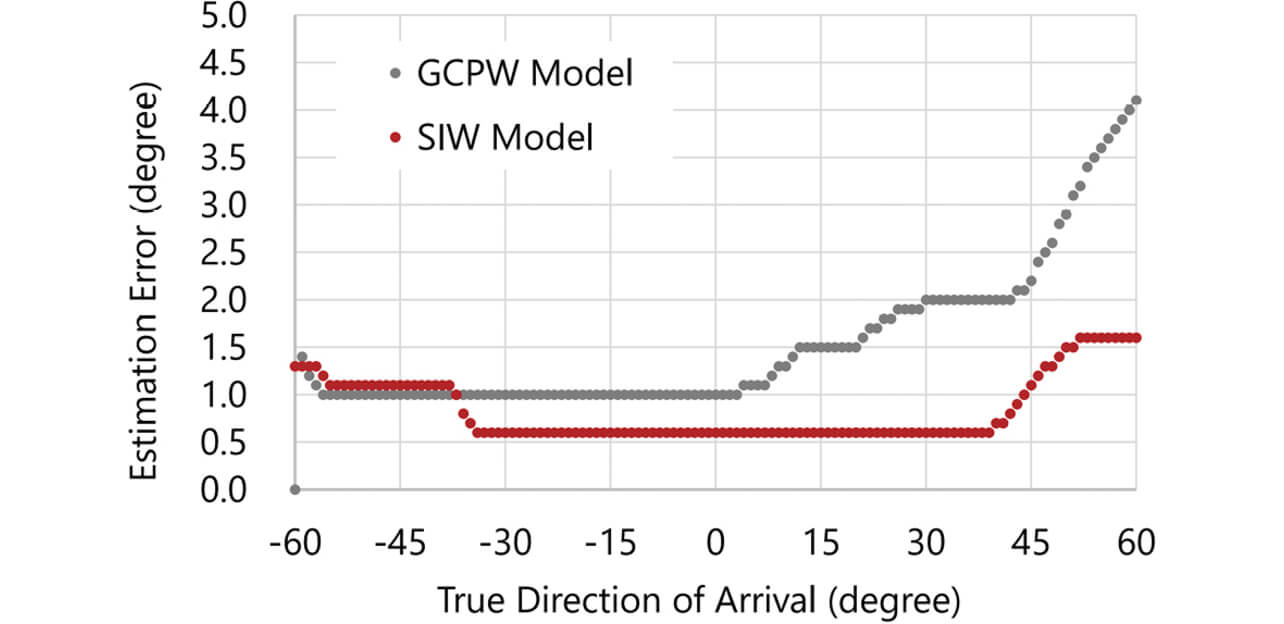
-60° ≤ θs ≤ 60°の範囲で見たとき、GCPWでの推定誤差は最大で4.1°に達するいっぽう、SIWモデルでは1.6°と比較的小さい値に抑えられていることがわかる。すなわち、伝送線路をGCPWからSIWに置き換えることによって、目論見どおり到来方位推定精度が向上する傾向が示された。
4.4 到来方位推定精度のさらなる向上
GCPWをSIWに置き換えることによって、到来方位推定精度が大部分の方位について改善されることを示した。しかし、-45°近傍など一部の方位についてはGCPWよりも劣る結果となった。この原因として寄生素子とSIWとが近接しているために、寄生素子に不要な電流が流れていることが推定された。寄生素子に不要な電流が流れることは、SIWモデルのTx1に接続したポートに給電した際の電流分布のシミュレーション結果(図8)によっても裏付けられた。
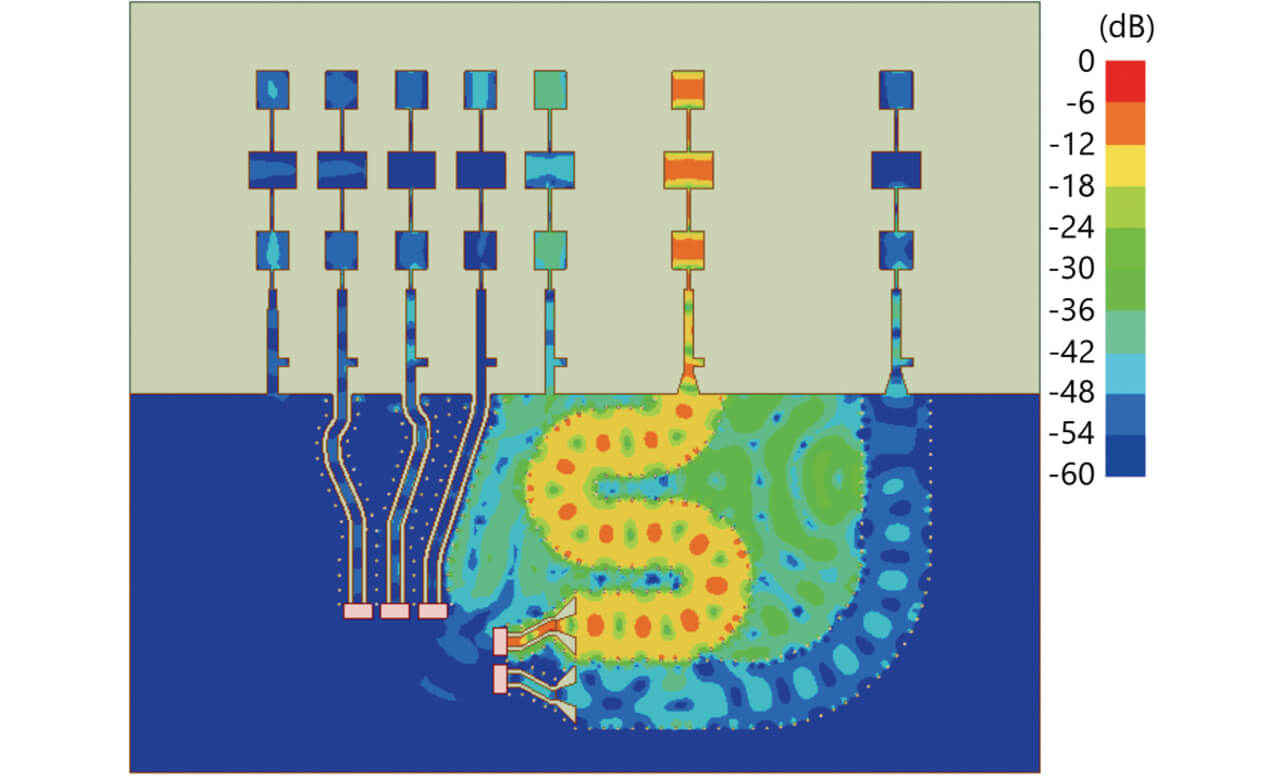
そこで、図9のように寄生素子を削除したところ、到来方位推定精度が向上し、すべての方位についてGCPWモデルよりも到来方位推定誤差が小さくなる結果を得た(図10)。なお、このときの到来方位推定誤差の最大値は1.2°であった。
以上のように、今回検討した形状のアンテナにおいて、寄生素子を削除することで、到来方位推定精度が向上することが明らかになった。この結果は、他の形状のアンテナにおいても、寄生素子を削除したり、伝送線路から寄生素子に流れる電流を抑制したりすることで、到来方位推定精度が向上する可能性を示唆している。
5. むすび
プリント基板上に形成されるミリ波レーダにおいて、伝送線路からの電波の放射が大きいと到来方位推定精度が劣化する。そこで本稿では、空間への放射が大きい伝送線路であるGCPWの替わりに放射の小さいSIWを導入することによって、到来方位推定精度が向上することを電磁界シミュレーションを用いて示し、定量的に効果を明らかにした。具体的には、従来のGCPWモデルで4.1°であった到来方位推定精度がSIWを導入することで1.2°まで改善した。
SIWの導入によって、ミリ波レーダを用いたセンシングにおける位置の推定精度が向上し、車載や交通インフラ、FA、ヘルスケアを含めた幅広い分野で、より高い精度でターゲットを検出するミリ波センシングの提供が可能となる。今後は、想定されるアプリケーションの利用シーンにおいて、実機を用いて効果を検証していく。
参考文献
- 1)
- 大橋卓,谷本雄大,齋藤啓介.アレー拡張処理を用いたミリ波レーダによる屋外人物の3Dイメージング.OMRON TECHNICS. 2022, Vol.54, No.1, p.92-100.
- 2)
- 一般財団法人 マルチメディア振興センター.“ミリ波レーダー(センサー)システム等に関する海外動向”.情報通信審議会 情報通信技術分科会 陸上無線通信委員会,2019-05-29. https://www.soumu.go.jp/main_content/000624368.pdf,(参照2023-02-08).
- 3)
- 情報通信審議会.“「小電力の無線システムの高度化に必要な技術的条件」のうち「60GHz 帯の周波数の電波を使用する無線設備の多様化に係る技術的条件」一部答申”.情報通信審議会,2021-03-30. https://www.soumu.go.jp/main_content/000741191.pdf,(参照2023-02-08).
- 4)
- Xu, J.; Hong, W.; Zhang, H.; Yu, Y. “Design and measurement of array antennas for 77GHz automotive radar application.” 2017 10th UK-Europe-China Workshop on Millimetre Waves and Terahertz Technologies (UCMMT). 2017, p.1-4.
- 5)
- Fan, Y.; He, M.; An, Z. “An Array Antenna for 24GHz Automotive Radar Application.” 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT). 2020, p.1-3.
- 6)
- Ye, Y.-J.; Chueh, H.-Y.; Chang, W.-C.; Liao, W.-J. “A Series-Fed Patch Antenna Array for Biomedical Radar Applications.” 2021 International Symposium on Antennas and Propagation (ISAP). 2021, p.1-2.
- 7)
- Deslandes, D.; Wu, K. Integrated microstrip and rectangular waveguide in planar form. IEEE Microwave and Wireless Components Letters. 2001, Vol.11, No.2, p.68–70.
- 8)
- Kazemi, R.; Fathy, A. E.; Yang, S.; Sadeghzadeh, R. A. “Development of an ultra wide band gcpw to siw transition.” 2012 IEEE Radio and Wireless Symposium. 2012, p.171–174.
Ansys HFSSは、米国ANSYS, Inc.またはその子会社の米国およびその他の国における登録商標または商標です。
本文に掲載の名称は、各社が商標としている場合があります。














