複数の照明の光度を調整できるマルチCH照明を持つ撮像系において、外観検査における照明条件とカメラの撮像条件を、容易に短時間で設定できるようにする問題を取り扱う。提案手法では、環境光、センサノイズ、暗電流オフセット、光度の量子化などのハードウェア特性の補正処理を構築することで、画像合成により、任意の照明条件におけるワークピース（検査対象の被写体）の撮影画像を精度良くシミュレーションする技術を確立した。これによって、最適化に必要な撮影数を、評価パターン数の対数オーダーに削減し、全ての発光パターンから1～2秒で（39CHの場合）最適解を探索完了できるようになった。また、従来技術では、照明装置の構成に依存して最適化アルゴリズムの修正が必要であったが、提案手法は、任意の配置構成のマルチCH照明装置で汎用的に動作する。構築した照明シミュレーション技術は、ティーチング作業の自動化並びにオフサイト化を実現可能な基礎技術となる。

1．まえがき

1.1 背景

製造現場における製品の外観検査は、機械による人員の置き換えが最も進んでいない分野の1つであり、将来の労働人口減少に向けて取り組まなければならない自動化の重要課題である。近年、ディープラーニングに代表される人工知能・機械学習技術の発展によって、検査の自動化技術は飛躍的に向上しつつある。しかしながら、外観検査並びにマシンビジョン一般において、検査システム構築で手間がかかる作業は、照明条件の最適化を含む撮像系の設計であり、この分野の自動化はあまり進んでいない。難易度が高い事例において人が手作業でこの作業を行う場合、ワークピースの個体ばらつきに対応しつつ欠陥を確実に見えるようにするために、対象となるワークピースを1つ1つ交換しつつ、照明を手作業で調整することと、検査アルゴリズムを検討・検証することを交互に繰り返す必要があり、所望の検出性能を得るために大変多くの工数を必要としてしまう問題があった。

この照明の最適化問題を取り扱う際の難点は、どのように照明を点灯させるとどのような撮像画像が得られるのかが分かっていない場合、実際に撮影ステージで多数のワークピースを載せ替えつつ撮影を繰り返す以外に、照明の点灯状態を探索する方法がない点である。このようなハードウェア的な制約があると、最適解を求めるための試行回数が十分に確保できず、作業工数内で最適解を得ることができない。

本稿では、この問題を解決するために、照明シミュレーション技術をベースとしたマルチCH照明最適化技術を提案する。本稿で言う照明シミュレーションとは、配光制御が可能な照明を含む撮像システム全体のシミュレーションを意味し、照明条件やカメラ設定が与えられた際に、推定された撮影画像を出力する、所謂、順方向の問題を扱うものである。このシミュレーションが可能であれば、撮像画像を評価して、最も検査に適切な照明条件を探索することが可能となる。照明シミュレーション技術によって実現される価値としては以下のものが挙げられる。

（1）

撮像系ハードウェアを伴う最適化問題が、PC上の数値計算の問題へと置き換えられ、検査アルゴリズムにとって良い照明、照明条件にとって良いアルゴの同時最適化を、既存の数値最適化の手法によって解決することができる。

（2）

実際に撮影された多数のワークピースの個体／搬送ばらつきに対して直接最適化されるため、人手で最適化を行うのに比べてより多くのサンプルを俯瞰して、より良い設定を探すことができる。

（3）

照明条件や検査アルゴリズムの最適設定は、初回の撮影以降はオフサイトの（PC 上に閉じた）作業となるため、最適化の作業において、検査装置やサンプルのワークピースのリソースを占有しない。

（4）

ワークピースの新しい個体ばらつきモードが発生し、検査を再調整する必要が生じた場合に、既にこれまでに撮影してきた多数のワークピースで、再撮影を伴う再検証をするという手間のかかる作業が必要なくなる。

配光制御が可能な照明装置としては様々なものが考えられるが、マルチCH照明と可動照明に大別される。前者は、複数の照明の光度を個別に調整できるものであり、角度分解能を上げるとチャネル数が膨大になってしまうという問題があるが、可動部が存在しないため耐久性が高い。欠陥の見えやすい照射角から光を当てたり、同時に多くの角度から照射することで、検査に不必要なテクスチャを抑えたりすることができる。一方、後者の可動照明とは、照明の配置を変えることで配光を変化させるタイプであり、手作業で設置場所を最適化するケースも含まれる。こちらの場合においては、数理的な最適化問題に持ち込むためにパラメトリックに自動で配光を制御させようとする場合にはメカ機構が必須となってしまう。

本稿では、これらのうちマルチCH照明を扱う。理由は、照明シミュレーションを画像の加減算による重ね合わせ合成という非常に単純な演算で精度良く実現できるためである。他方、可動照明の場合には、精度の高い照明シミュレーションを実現するのは難易度が高いため、検討の優先度を下げ本稿では取り扱わない。本稿で取り扱う照明シミュレーション技術は、マルチCH照明であれば適用可能であり、特定の装置に依存してはいないが、実験では39CH（方位13、色3）を持つFHシリーズ向けの照明装置FL-MD180MC（図1）、FL-MD90MCを利用した。

1.2 関連研究

この問題に対する既存技術として、照明パターンを様々に振って実際に撮影を繰り返し、判別分析による評価指標が最も高いものを選択する手法^1）が報告されている。評価指標としては本稿でも判別分析を用いているが、提案手法は以下の2つの点で優位性がある。

1つは、最適化の所要時間である。照明CH数を、光度の量子化レベル数を、露出の取りうる数をとすると、照明条件の場合の数は*）となり、CH数に対し指数関数的に増加してしまうため、CH数が多いと全ての撮影条件で撮影して調べあげるだけでも膨大な時間がかかってしまう問題がある。本稿はこの問題を鑑みて検討されたものであり、提案手法によれば、必要な撮影の数をおおよその定数倍へ削減させることが可能となる。また、既存技術では、撮影数が膨大となる問題を粗密探索アルゴリズム^1）によって効率的に探索することを提案しているが、照明CHの配置情報を基に人が経験に基づき探索アルゴリズムを毎回設計する必要が生じてしまう。本稿の提案手法は、照明CHの具体的な配置に依存しないように最適化アルゴリズムを設計でき、任意のマルチCH照明装置に対して汎用的に利用できるアルゴリズムを構築できる。

もう1つの違いは評価関数の作りやすさである。一般に外観検査においては、ワークピースの統計的ばらつきを取り扱うため、1つのサンプルというより複数のサンプルに対する評価関数を用いた最適化が求められる。提案手法では全てのサンプル画像を同時に用いた任意の評価関数で照明最適化を行うことが可能となる。加えて、照明設計の問題設定が、複数の検査要件のバランスをとって成立させるような、目的関数を事前に一意に書き下すことのできない多目的最適化問題であった場合には、目的関数を修正しつつ対話的に解を更新してゆく必要があるが、提案手法では目的関数を変更しても再撮影の必要はないためレスポンスが早く、優れた操作性を実現できる。

本稿と同様に、撮像シミュレータを用いた撮像系の最適化としては、機械学習的な手法によって撮像系の振る舞いを近似させるProxy Modeling^2）も検討されている。

1.3 記号

ボールドの小文字はベクトルを示し、ボールドの大文字は行列を示す。それ以外はスカラーである。はベクトルに対するノルムを示し、は行列Xのi行j列の要素を示すものとする。

2．画像合成による照明シミュレーション

制御自由度のある照明・撮像系の最適化問題を扱ううえで、撮像系シミュレータが精度良く構築できることは重要である。本稿では、マルチCH照明の場合には撮像シミュレータが簡単な画像合成（画像の重ね合わせ）で実現できることに注目し、実際のデバイス特性を補正することによって高い推定精度を実現できる。

2.1 基底発光パターンによるワークピース評価画像の取得

画像の重ね合わせによる照明シミュレーションのため、撮像システムにおけるセンサのリニアリティ（輝度と画素値の間のリニアリティ）が成立していると仮定する。これはつまり、カラーフィルタのデモザイキングなどの信号処理を含め十分にリニアであると見なすことができ、暗電流オフセット補正によって輝度ゼロにおいて画素値がゼロとなっており、画素飽和による非線形を避けるために、HDR（High dynamic range）合成を含んだ撮影処理がされているという意味である。そのようにして撮影された画像を輝度画像と呼ぶことにする。検査時において、個のマルチCH照明で照らしたワークピースを撮影する状況を考え、各照明CHの相対光度（光度の定数倍となる量）を以下の相対光度ベクトルとして表記する。

（1）

ティーチングにおいて、1つのワークピースについて照明発光パターンを回変化させて撮影し、最適な検査時の照明条件を決定することを考える。（1）枚目の撮影における相対光度ベクトルを次のように定義する。

（2）

これらの発光パターンによってワークピースを撮影することで、任意の発光パターンで照らした場合のワークピースの撮影画像を再構成することが可能となる。これはLT（Light Transport）行列^3）の推定を行っていることと等価となる。一般にLT行列の全ての自由度を取得するためには、=(,）つまり線形独立となるように発光パターンを決定することが望ましい。個の照明の自由度を全て余すことなく活用させるためには、少なくとも=であり、その際にはフルランクとなっている必要がある。

一方、＜だと照明個数の自由度を十分に活用できないが、ワークピースの撮影時間を短縮させることができる。この状況は、プロジェクター照明など制御自由度Kの非常に大きい問題設定で発生する。代表的なものとしてCompressed Sensingを用いたLT行列推定^3）を行う手法が挙げられる。

また、＞とするケースも考えられ、これは照明の自由度を十分に活用させるという意味では必要以上であり無駄な撮影枚数となるが、比やダイナミックレンジを稼ぐなどの別目的で選択されうる^4）。

発光パターンで撮影された輝度画像を基底画像と呼ぶことにする。基底画像をコラムベクトルとして並べたものをとして、これらを枚分横に並べた行列=［,...,］を用いて、検査時の相対光度ベクトルとその際の輝度画像は以下のように表現される。

（3）

（4）

ここで、は各発光パターンの混合比を示すベクトルである。各照明CHの光度レベル値（量子化された光度階調のレベル値）はこれを元に算出されるが、この値そのものではない。これは一般に負の値をとることも許されるが、照明の発光パターンは必ず非負でなければならないため、以下の条件が課せられる。

（5）

ここで、ベクトルや行列に対する不等号は、全ての要素についての不等号であるとする。=つまり、照明を1つずつ点灯させて（=）枚撮影した場合には、とは等価となる。以下では、最適な画像合成重みを求めることによって、その際の最適照明を求める問題を扱う。

2.2 センサモデルと画像合成の評価式

露出時間で撮影された画像ベクトルを、露出における画像ベクトルに変換するモデルは、画素飽和を考慮しない場合、次式のようにオフセットつき線形モデルで示される。

（6）

ここで、（1）はカメラのカラーフィルタ色インデックス、は暗電流オフセット値でありキャリブレーションによって予め求めておくものとする。センサがこのモデルに従う場合、マルチCH照明の画像合成による照明シミュレーションは次式で表現される。

（7）

ここで、は撮影された基底画像のコラムベクトルである。基底画像はそれぞれがAEC（Automatic Exposure Control）またはHDR撮影されているため、基底のインデックス（1）ごとにそれぞれ異なる露出やゲインで撮影されている。は露出における合成された撮影画像ベクトルである。は画像合成ウェイトであり、照明CHへの光度レベル値と露出設定から最良なものが一意に決定される。

3．検査に最適な照明条件の決定

3.1 評価基準クロスエントロピー vs. SN

外観検査における照明設計の目的は、良品と不良品が正しく判別されるようにすることである。いま、判定基準として既定の判別アルゴリズムが与えられた場合、照明最適化問題は、良品/不良品の判別を正解と一致させる「クロスエントロピー最小化問題」として定式化される。もし判別器が機械学習器であった場合、照明最適化と判別器の学習を同時に行い、お互いにとって最も性能を発揮するように同時最適化させても良い。

しかしながら、クロスエントロピー最小化を行わせようとする場合に大きな問題となるのが、良品/不良品ラベルの付加されたサンプルが大量に必要であるという点である。これは、多くのサンプルが得られない立ち上げ時には利用方法として大きな課題となる。特に大きな自由度を持つ照明装置を最適化させようとする場合、少数の良品/不良品ラベルを判別させるだけという基準では、最適な照明はいかようにもできてしまう（一意に決められない）という問題が生じてしまう。

この問題を解決するために、本稿ではユーザーが指定した前景と背景を乖離させるという意味でのSN比の最大化を採用する。これは、画像自体の評価基準（コントラスト、明るさ、近さ）をベースとして照明を最適化する手法である。このように考えた場合、外観検査における照明設計に求められる要件としては、主に以下2つが挙げられる。

（1）

良品と不良品の判別がしやすい特徴を見えやすくすること
（つまり欠陥を見えやすくすること）

（2）

良品ばらつきを見えにくくすること

両者は一般に相反する性質であるため、それらのバランスの取れた照明を設計することが最適化の難課題となる。

3.2 2次形式による評価関数の高速化

2.2で述べたように、基底画像は階調を高い精度で測定するために、異なる露出時間で撮影されている。そのため、画像合成ウェイトは露出の違いも含めたものとして定義されており、求めるべき照明CHの相対光度そのものではない。を任意に定めた基準露出、（1）は各基底画像の露出であるとすると、求めるべき照明CHの光度の比を示すベクトルは次のように表現できる。

（8）

本稿では画像の評価基準を高速に評価するため、評価関数を2次式に限定させるというアプローチをとる。式（4）より、合成画像は=として表現できる。ここでは以下で定義される基準露出における基底画像を並べた行列である。

（9）

これを用いて、コントラストはToeplitz行列をハイパスフィルタとして、明るさはを画素平均として、画像の一致はとして表現できるため、行列を×の半正定値行列として、これらは全てのような2次形式として表現される。画像の分散や線形部分空間への射影誤差についても同様に2次形式となる。一方、別の評価関数として、予め指定した画像と一致させる場合は、指定した明るさや色にするならを画素平均として、特定部分の発光パターンを固定して残りを最適化する場合にはとなり、これらは全て2次式となる。

このように2次式の係数で表現することによって、画像のピクセル数に依存せず、高速に評価可能な評価関数を表現できる。注意すべきは、これらの表現は画素飽和が生じてしまうと不正となってしまう点である。それゆえ、画素飽和させない範囲での最適化とし、飽和を含める際には行列による簡略化は使用せず、画像を毎回生成して飽和によるクリッピングをした後で、直接ノルムを計算する。

3.3 Fisher線形判別による照明設計

Fisher線形判別とは、「クラス内分散を最小化」かつ「クラス間分散を最大化」する射影ベクトルを求めることができる手法である。この手法では、特徴ベクトル生成のための演算は単なる内積であるため、非線形な演算を取り入れた手法と比較すると効果は非常に限定されている。しかしながら、本稿で取り扱う照明条件の最適化においては、マルチCH 照明による撮像を演算と見なすと数学的には単なる内積演算および線形射影そのものであるため、最適な線形射影を求めることができるFisher線形判別を用いることは適している。以下では、画像のl2距離による近さ（類似度）に注目して、クラス内分散とクラス間分散を定義し、それによってFisher線形判別を実現するマルチCH照明発光パターンを算出する問題を定式化する。

いま、一般にワークピースを個のカテゴリに判別する問題を考える。例えば良品と不良品に判別する場合には=2となる。カテゴリのインデックスは1とする。また、画像の関心領域（Region of Interest:ROI）間の比較対象として(1)個のグループを持つものとする。照明の最適化基準は、これらの同一グループに属する画像群のばらつきの大きさによって定義される。ROI比較対象グループのインデックスは1とする。ユーザーの指示により各とpの組み合わせについて、ワークピース画像からROIを抜き出した画像集合が与えられているものとする。

ティーチングに用いるワークピース画像は、マルチCHの個々を既定の（評価用）発光パターンに従い点灯させて撮影されているものとする。これらを用いて、クラス内距離（良品ばらつき）の期待値と、クラス間距離（欠陥の見やすさ）の期待値を次のように距離として定義する。

（10）

（11）

(,）はマルチCH画像の集合と平均から算出される分散であり、以下の定義である。これは、照明ベクトルの2次形式として表現でき、このときの係数行列をと表記する。

（12）

ここで、はKronecker積、vec=であり、行列とは以下のように表現される。

（13）

（14）

ここで、,はそれぞれ、行列,のi番目のコラムベクトルである。,の2次形式の係数行列をそれぞれ,とすると、Fisher線形判別では、クラス間分散の最大化とクラス内分散の最小化を同時に実現するために、以下の評価式を最大化させる。この式の意味するところは、背景ばらつきに対して前景がどれだけ乖離しているかというSN比を最大化していると見なすことができる。ここで、2次形式でさえ表現されていれば、3.2で述べられている任意の評価式を用いてもよい。この式を最大化させるが求めるべき画像合成重み、すなわち最適照明条件となる。

（15）

のノルムを制約する意味は、評価関数のみでは不定となってしまうためである（を定数倍しても評価値が変わらないため明るさが決まらない）。Fisher線形判別の最適射影方向は、Lagrange未定乗数法により一般化固有値問題における最大固有値に対応する固有ベクトルとして求めることができる。しかしながら、照明最適化においては固有ベクトルが負値を持ちうることが問題となる。つまり、固有ベクトルに沿う方向で照明強度ベクトルを設定すればよいのであるが、負の照明強度は実現できないという問題が生じる。これに対する解決策は大きく2つ考えられる。

最初の解決策は、照明強度ベクトルに対し非負条件を入れて最適化問題を解くものである。本稿では、限定されたケースであれば数理計画法が適用可能であることを示す。

次の解決策は、正値のみと負値のみで2つの組に分け、負値のものは絶対値をとりそれぞれの組について撮影し、後段の画像処理上にてそれらの撮影画像の差を取ることで、疑似的に負の照明強度を実現するものである。これによって、元の正値と負値が混在する固有ベクトルで直接撮影したのと同等の効果を得られるが、最低2回の照明条件を変えた撮影が必要になってしまう。本稿はこのようなマルチショット検査を検討に含めない。

3.3.1 半正定値計画法による解法

ここでは、最大化すべきSN比を定義する前景と背景のペアが1つである場合においては、次式で示されるFisher線形判別の最適化問題は、数理計画法によって非負条件で照明最適解を高速に算出できることを述べる。

（16）

ここで、0という表記は、ベクトルのすべての要素が非負であるという意味である。この問題は、一般性を失うことなく以下のように変形できる。

（17）

これは、Nonconvex-QCQP（Quadratic Constrained Quadratic Programming）問題として知られ、一般にNP困難であるが、このケースでは半正定値緩和^5）を行うことができ、SDP（Semidefinite Programming：半正定値計画問題）で解くことが可能である。具体的には、を半正定値行列であるとして置き換えてしまい、次のような最適化問題へ変形する。

（18）

ここで、=trは行列のFrobenius内積を意味し、0は行列の全要素が非負であること、≽0は行列が半正定値であること、=は対称行列であることを意味する。この問題はSDPソルバーによって高速に最適解を求めることができる。解はSDPの拘束条件の数より、ほぼランクが1となることが知られており^5）、その場合=と近似できるため、==を固有値分解して固有値最大に対応する固有ベクトルを求めることで最適解となる相対光度ベクトルを得る。Perron-Frobeniusの定理より、0のときは0となることが保証されているため、最適解はすべて非負の照明設定値としてそのまま利用できる。

3.3.2 多目的最適化による解法

前述したSDPによる解法では、1つの前景と背景のペアからなるSN比の最大化しか取り扱うことができないうえ、明るさの最適化など、1次項まで含まれる2次式を含む最適化問題を取り扱うことができなかった。もし、複数の前景と背景のペアからなる複数のSN比を同時に最大化させようとしたり、明るさやコントラストを所望の値に近づけようとしたりすると、複数の目的関数のバランスをとって最大化させる多目的最適化問題を解く必要がある。この問題を扱うために本稿では、個々の目的関数の重みづけ和を最大化させ、多数の試行によって重みづけを調整して適切なバランスを実現させる加重和法^6）を採用する。最適化には逐次二次計画法（Sequential Least Squares Programming:SLSQP）を利用した。

4．評価実験

4.1 システム構成

評価実験で用いたシステム構成は、オムロンの画像処理システムであるFHシリーズをベースとしている。マルチCH照明はFL-MD180MC,FL-MD90MCを、カメラはFH-SCX12,FH-SMX12,FH-SCX05,FH-SMX05を用いた。また、基底画像撮影の際に環境光が入らないように、撮影ステージを暗室内に設置した。基底画像を撮影するためのAEC,HDRによる撮影アルゴリズムや、暗電流オフセット補正、光度レベル値－輝度LUT補正のキャリブレーション機能は、FH内の処理ユニットとして実装した。それ以外の最適化アルゴリズムやUIは、FHとLAN接続されたPC内で動作する。

4.2 UI

作成した照明最適化のティーチングUIを図2に示す。①で基底発光パターンとAEC,HDRなどの撮影方式を選択してワークピースを撮影する。②で撮影されたワークピースを選択し③で評価基準と多目的最適化の荷重ウェイトを入力する。評価基準の入力においては、複数のワークピースを同時に参照できるようになっている。最適化を実行すると解のリストが④に表示され、③において複数の目的関数の評価値を確認しながら解を比較検討できる。解が選択されると光度レベル値が⑤に表示される。問題の設定によっては明るさの1 軸は決定しないため、⑥によってスケールを調整できるようになっている。撮影条件が決まると⑦によってシミュレーション画像と実写を切り替えながら、⑧に表示されるワークピース画像の比較ができる。

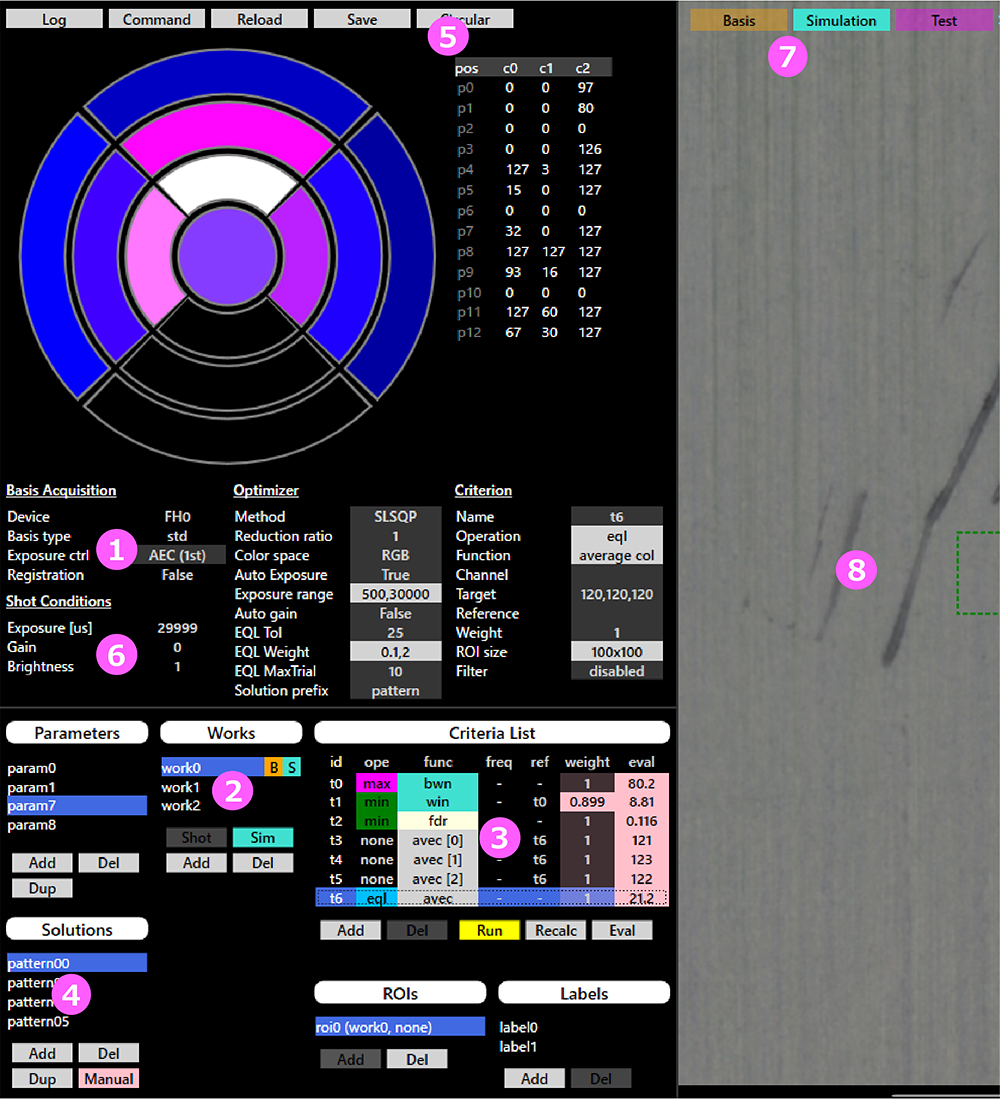
4.3 ソフトウェア実装と実行時間

数値計算はPythonで実装した。行列計算はNumpyを用いているが、式（14）の内積演算に最も時間がかかるためマルチスレッドや画像縮小の前処理を用いている。式（18）のSDPによる最小化には、CvxOpt^7）の実装を利用した。=39の場合の最適化の平均的な所要時間は1～2秒程度である。多目的最適化には、SciPy^8）に実装されているSLSQPを利用した。局所解を回避するために、初期値を回振って複数回最適化を実行し、最も良い解を選択するようにした。初期値を回振って最適化しても所要時間は1秒程度である。

4.4 環境光の漏れ込み対策

画像センサに照明機器以外からの環境光が混入してしまうと実写とシミュレーションの画像差異の要因となる。

対策として、基底画像の撮影において環境光の影響を相対的に小さくするために、照明の光度を常に最大として撮影し、カメラの露出を調整して飽和を回避させる撮影方法を導入した。（AEC撮影）

更なる環境光の対策方法として、環境光はマルチCH照明において常に点灯している照明が1つ存在していることに相当するため、ワークの基底画像の撮影時に照明機器を全消灯させて、環境光画像を1枚撮影すれば補正処理を構築できる。この手法によって、室内環境において問題ないレベルの環境光補正ができることを確認している。本稿では、環境光の影響がない状態でシミュレーション性能を検証するために、ワークピースを暗室内で撮影した場合の結果を掲載している。

4.5 実写とシミュレーションの画像比較

様々なワークピースと発光パターンにおける、画像合成シミュレーションと実写の比較を図3に示す。

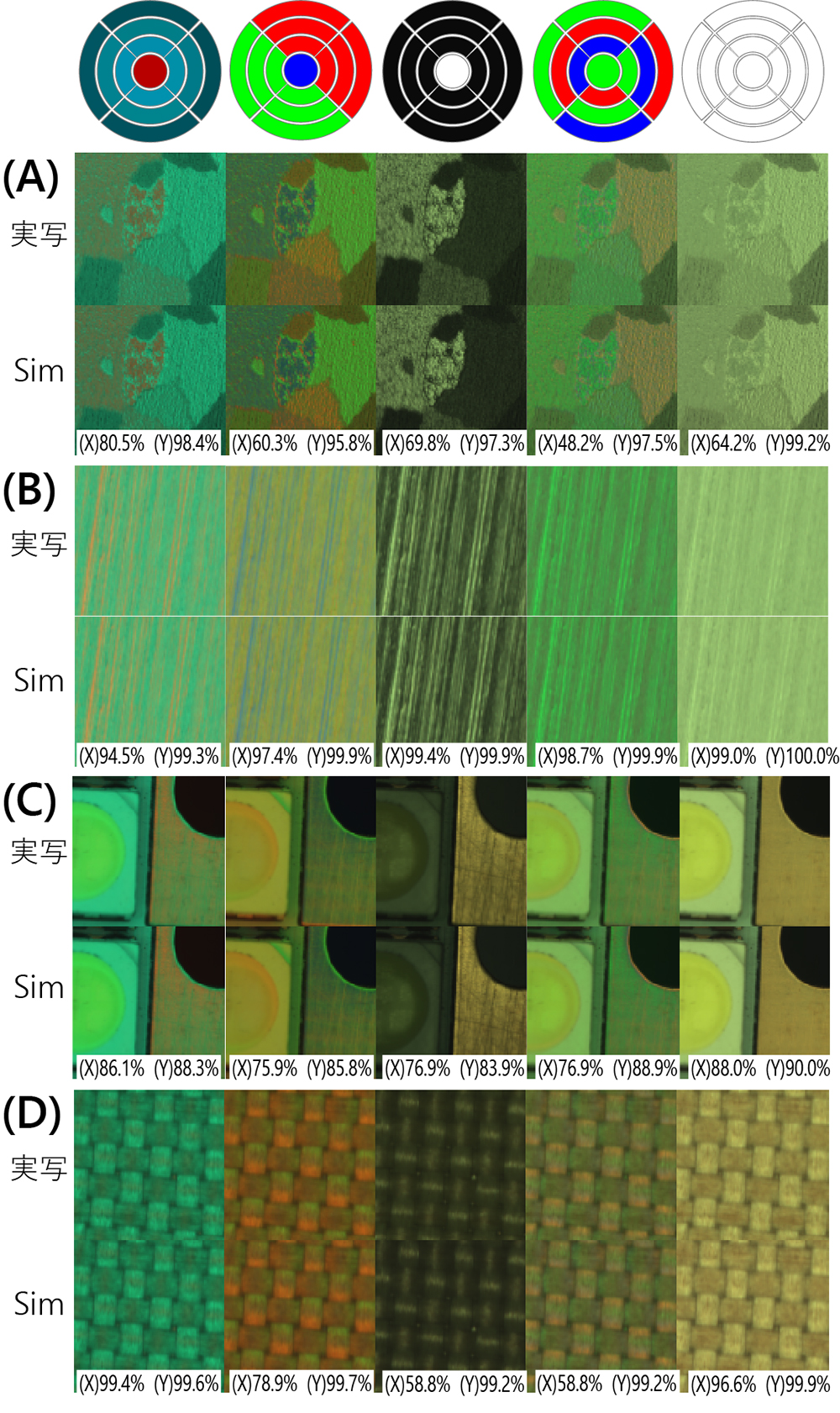
並べて見比べると違いが分かりにくいが、最大で±0.1倍程度の明るさのずれと色回り（色CHごとの明るさずれ）が生じている。明るさのずれは電源の特性が原因であり、色回りは暗電流オフセット値の推定ずれがAEC撮影の露出変換で強調されて起きていると考えられる。補正による改善は可能であると考えられるが、照明最適化の用途では現状の性能で十分であると判断し検討していない。

図中の（X）は、明るさのずれが理想的に補正された場合において、シミュレーション画像の画素値が、実写画像20回におけるショットノイズの3σの範囲内である画素数の割合を示しており、同様に（Y）は、色回りまで理想的に補正された場合のそれを示している。これらを補正できれば、ほぼショットノイズの範囲内に推定可能であることが分かる。ワークピース（C）において（X）（Y）の割合が低いのは、明暗のダイナミックレンジが広いため暗部分のノイズの影響を受けているためである。

その他の特記すべき不一致として、図4に示すように、飽和付近の白にじみの程度が若干異なることが挙げられる。センサが画素飽和すると非線形な特性が生じて階調の情報が失われてしまう。そのため、飽和した画素との間でデモザイキングによる補間処理がされると画像合成と実写の不一致の要因となる。この現象は、飽和領域付近の白にじみの強さの不一致として現れるが、原理的なものであり補正処理による対策はできていない。

4.6 SNを振った最適化

前景と背景のSN比を式（10）（11）（15）によって定義し、として複数の背景の分散、としてキズと背景の距離とする。SN比をいろいろな強さに振って最適化ができるように、背景消しの強さを示すパラメータを導入し、=［+（1-）］のように再定義した。金属ヘアラインのワークピースについてを10段階に振ってSDPによって最適化した結果を図5に示す。背景消しの強さに従ってSN比（/）が変化しているのが分かる。前景背景ともに、最もコントラストが強いのは=0 であるが、前景と背景の強さの比（SN比）が最も大きいのは=1.0であり、背景と背景の判別性が向上している。

=1.0で照明色が変化しているのは、画像の色チャネルを含んでのl2距離の意味で背景をフラットにするために、少しでも有利な色が選ばれるためである。

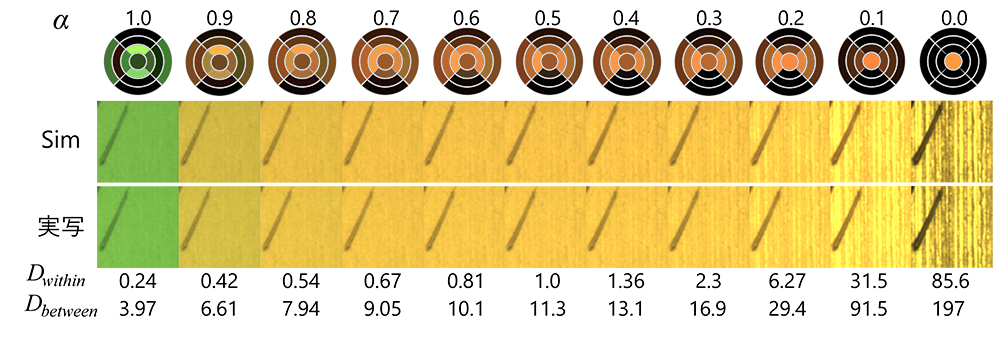
このワークピースでは、ヘアラインのコントラストは同軸照明（中心部）とリング照明（周辺部）の強度比バランスによってほぼ決定される。コントラストを出そうとすると同軸照明だけが選択されるようになり、逆に弱くしようとすると同軸とリングの同時点灯となる。の値が大きくなると照明パターンが複雑になっているが、この場合においては、これらとほぼ同程度な性能の、より単純な照明パターンを見つけることは可能である。理由は、行列がランク落ちに近くなっており、同じ性能を達成する照明パターンが一意に決定しない現象のためである。これはいわゆる過学習の状態であり、これを回避するにはワークピースのサンプル数を増やすか、画素値（明るさ）などの拘束条件の数を増やすか、基底発光パターンHを適切なものに選ぶとよい。事実、=1.0の照明パターンではワークピースを90度回転させるとヘアラインが見えてしまうが、基底発光パターンを回転対象なもので最適化することによって回転にロバストな照明パターンを得ることができる。

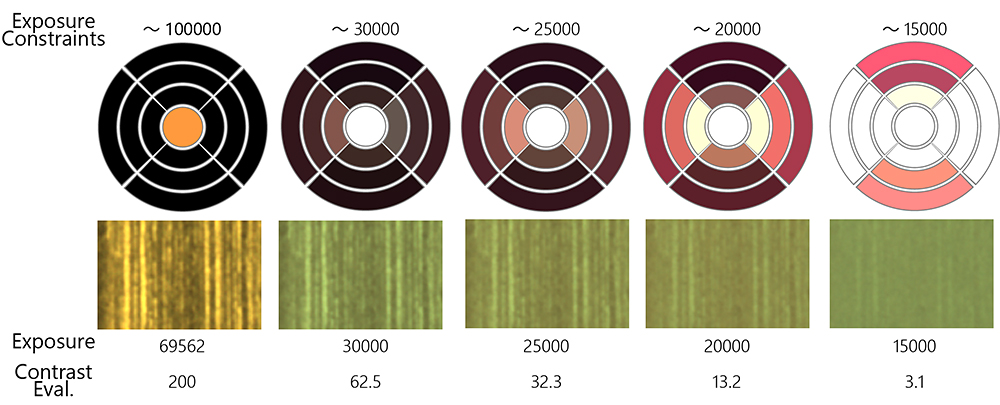
4.7 画素値（明るさ）を含めた最適化

図6では、多目的最適化によって、画素値（明るさ）を指定しつつ、コントラストを最大化するように最適化した例を示す。金属ヘアラインで最もコントラストが高くなるのは同軸照明であるため、露出の制約が最も緩い左側の例では、同軸照明のみが選ばれている。一方、右側は徐々に露出時間の制約を厳しくしたものであるが、それにつれ同軸照明だけでは照度が不足してしまい、指定された画素値を実現させることができなくなってしまう。そのため、複数の照明を同時に点灯させて明るさを稼ぐように最適化されており、その結果コントラストが犠牲になったことが確認できる。これは、指定された明るさを出せる範囲内で最もコントラストを最大化するように照明が最適化されたことを示している。このように、露出とコントラストのトレードオフ問題を、多目的最適化によって数値計算のみで俯瞰できることは、画像合成による照明最適化手法の大きなメリットである。

5. むすび

本稿では、外観検査向けのマルチCH照明の最適化問題に、画像合成による照明シミュレーション技術を用いることを提案した。精度の高い照明シミュレーションが可能であり、最適化に必要な撮影数を、評価パターン数の対数オーダーまで大幅に削減できることを示した。提案技術は、検査パラメータ設定を含めたティーチング作業の自動化やオフサイト化を実現可能な基礎技術である。

今後の展開としては、マルチショット検査や後段の検査も含めた同時最適化への拡張、多目的最適化の操作性向上、ワークピースばらつきシミュレーションを用いた照明最適化によるサンプル範囲外のばらつき対応が考えられる。

参考文献

1）

林 信吾．外観検査における照明パラメータ高速自動決定技術，OMRON TECHNICS. 2020, Vol.52, No.1, p.30-34.

2）

Tseng, E.; Yu, F.; Yang, Y.; Mannan, F.; Arnaud, K.S.; Nowrouzezahrai, D.; Lalonde, J. F.; Heide, F. Hyperparameter Optimization in Blackbox Image Processing using Differentiable Proxies. ACM Transactions on Graphics （TOG）. 2019, Vol.38, No.4.

3）

Chiba, N.; Hashimoto, K. “Sparse Estimation of Light Transport Matrix under Saturated Condition”. The 29th British Machine Vision Conference （BMVC2018）. 2018.

4）

Schechner, Y. Y.; Nayar, S. K.; Belhumeur, P. N. Multiplexing for Optimal Lighting. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2007, Vol.29, No.8, p.1339-1354.

5）

Luo, Z.; Ma, W.; So, A. M.; Ye, Y.; Zhang, S. Semidefinite Relaxation of Quadratic Optimization Problems. IEEE Signal Processing Magazine. 2010, Vol.27, No.3, p.20-34.

6）

Miettinen, K. Nonlinear Multiobjective Optimization. Kluwer Academic Publishers, 1999, p.78-84.

7）

Andersen, M. S.; Dahl, J.; Liu, Z.; Vandenberghe, L. “Interior-point methods for large-scale cone programming”. Optimization for Machine Learning. Sra, S., Nowozin, S., and Wright, S. J. eds. MIT Press, 2012, p.55-83.

8）

Jones, E.; Oliphant, T.; Peterson, P. et al. SciPy: Open source scientific tools for Python. 2001. http://www.scipy.org/,（参照 2020-2-1）．