垂直多関節ロボット動作の高速自動生成技術
- ロボット
- 経路計画
- 軌道計画
- 軌道最適化
- 干渉判定
近年、人件費の高騰や新型コロナウイルスの流行などの影響により、生産現場では省人化が求められている。省人化の手段の一つとして産業用ロボット、特に垂直多関節ロボットのニーズが高まっているが、高い生産性を実現するロボットの動作を生成するには大きな工数がかかるうえ、専門知識も必要となるため、普及が進んでいないのが現状である。そこで、本研究では垂直多関節ロボットを対象に、自動かつ高速に動作生成する技術を開発した。動作生成技術は経路計画技術と動作高速化技術の2つから構成されている。前者は状況に応じたアルゴリズムの選択と高速な干渉判定処理を実現することで、1動作の経路計画を既存技術の数秒から実時間対応可能な100msecに短縮した。後者は動作速度に対して効果の高い加速度パラメータの最適化とロボットの関節にかかる慣性を軽減する経路補正を行うことで、ロボットのデフォルトパラメータで動作させた場合と比べてタクトタイムを約20%改善できた。そして、これらの開発技術の効果を確認するために構築したばら積みピッキングシステムでは、ユーザーにロボット動作生成を全くさせることなく、人と同等のタクトタイム3秒で作業することができた。
1.まえがき
近年、人件費の高騰や新型コロナウイルスの流行などの影響により、生産現場では省人化が求められている。省人化手段の一つとして産業用ロボットの導入が盛んに検討されており、人の行っている作業の置き換えや協働のために、可動領域が広く動作の自由度が大きい垂直多関節ロボットのニーズが高まっている。しかし、実際の生産現場、特に中小企業においてはロボットの導入が進んでいない。この問題に関しては、ロボットの動作生成に時間がかかること、さらには、作業の難易度が高いことが、いくつかの要因のうち主なものとされている1)。
産業用ロボットに作業を行わせるには、ロボットが動く位置・姿勢を設定するティーチングと呼ばれる作業と、設定された動きの速度等のパラメータ調整作業により、動作を生成する必要がある。これらはどちらもロボットを実際に動かしてトライアンドエラーで作業するため時間がかかる。また、作業内容に関しても、関節角度によるロボットの制御やトルクの考慮など、いずれの作業についても専門知識と熟練が必要になる。
そこで、本研究では垂直多関節ロボットを対象に、位置姿勢の設定と動作パラメータの調整を自動で行うロボット動作自動生成技術を開発した。この技術により、ロボットの知識のないユーザーでもロボットを生産現場に導入できるようになる。また、本技術は1動作当たり100msec以下の計算時間で動作が生成できるため、ばら積みピッキングのような都度動作生成が必要なアプリケーションにも対応できる。
以下、2章では産業用ロボットによる動作生成の課題と開発目標について、3・4章では開発したロボット動作自動生成技術について、5章では開発成果をもとに実装したばら積みピッキングアプリケーションについて説明し、6章でまとめと今後の展望について述べる。
2.ロボット動作生成の課題と技術開発目標
2.1 ロボットの動作生成について
垂直多関節ロボットは関節のサーボモータの回転角度により制御される。各関節の回転角度の集合によって構成されるロボットの状態を姿勢(Posture)と呼ぶ。ロボットの動作生成は、単純にはロボットの動作開始姿勢(現在姿勢)から何らかの作業を行うための目標姿勢の二つを指定することで実現できる。このような制御方法をPTP(Point To Point)制御と呼ぶ。しかし、PTP制御による動作は単純に2姿勢間を線形補間でつないでしまうため、開始姿勢と目標姿勢の間に障害物があるようなときに干渉が発生してしまう。
これに対して、開始姿勢と目標姿勢の間の姿勢を細かに指定することで精密な動作を行わせる制御方式があり、これをCP(Continuous Point)制御と呼ぶ。CP制御のために与えられるロボットの開始姿勢と終了姿勢、およびその中間姿勢の集合のことを経路(Path)と呼ぶ。図1にPTP制御とCP制御による動作の違いを示す。
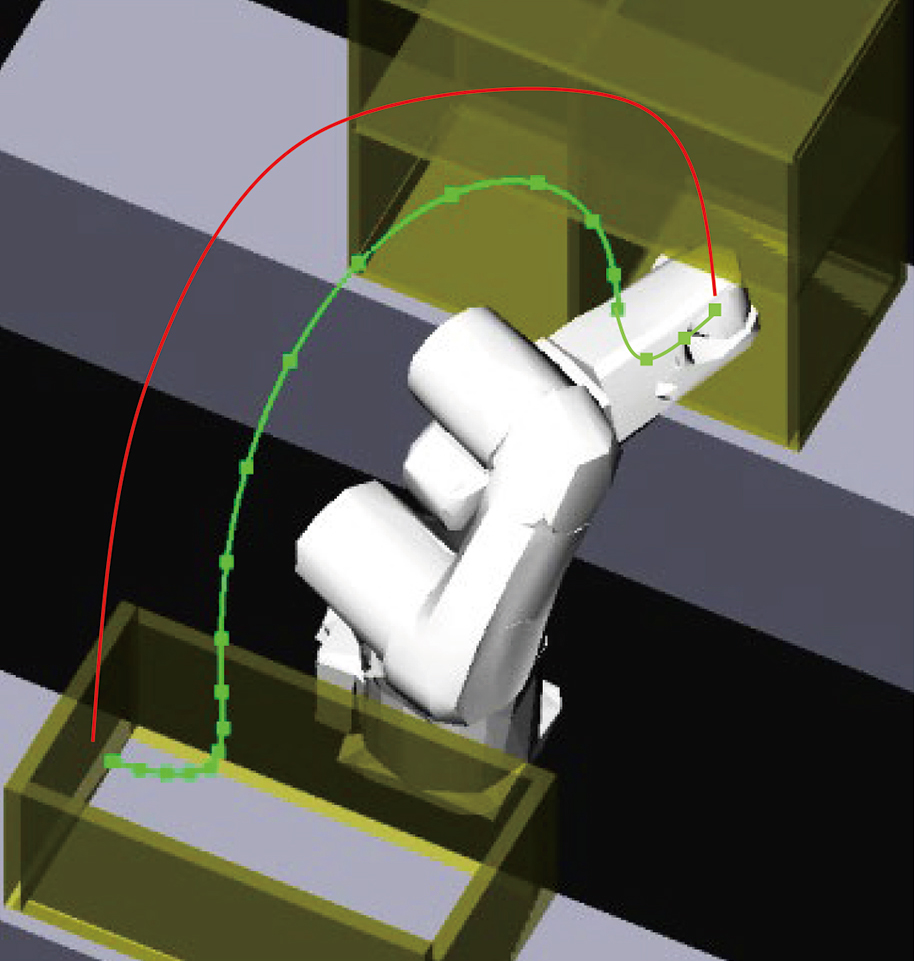
さらに、実際にロボットを動作させるには、設定した経路を時間とともにどのように実行するかを設定する必要がある。この時間的な変化は、サーボモータの回転速度・回転加速度などの動作パラメータを制御することによって実現できる。このように、動作パラメータを与えられて時間軸上で実行される経路のことを軌道(Trajectory)と呼ぶ。つまり、ロボットによる動作生成とは軌道を生成することと言える。
2.2 経路生成の課題
CP制御を行うための経路を生成するには、一般にティーチングと呼ばれる作業を行う。これは、人がティーチングペンダント(TP)と呼ばれるロボットの操作装置を使ってロボットを実際に動かして、経路を構成する姿勢を逐一登録する作業である。ティーチングで与えられる姿勢のことを教示点とも呼ぶ。
作業の複雑さや量にもよるが、一般にロボットを生産設備として使用するには数十から数百の教示点が必要と言われている。正確に教示点を設定するためには、ロボットの動作速度を落としたり停止させたりしながら姿勢を検証する必要がある。したがって、ティーチングには大きな工数がかかるという課題がある。
また、教示点として与える姿勢をとらせるためのロボット操作は熟練を要するという課題もある。これは、人が空間を縦横高さと傾きという直交座標系(実空間)に基づいて認識しているのに対して、ロボットを動かすパラメータが関節の回転角度(関節空間)というギャップがあることに起因する。図2に平面を動く2軸のロボットを例に説明する。
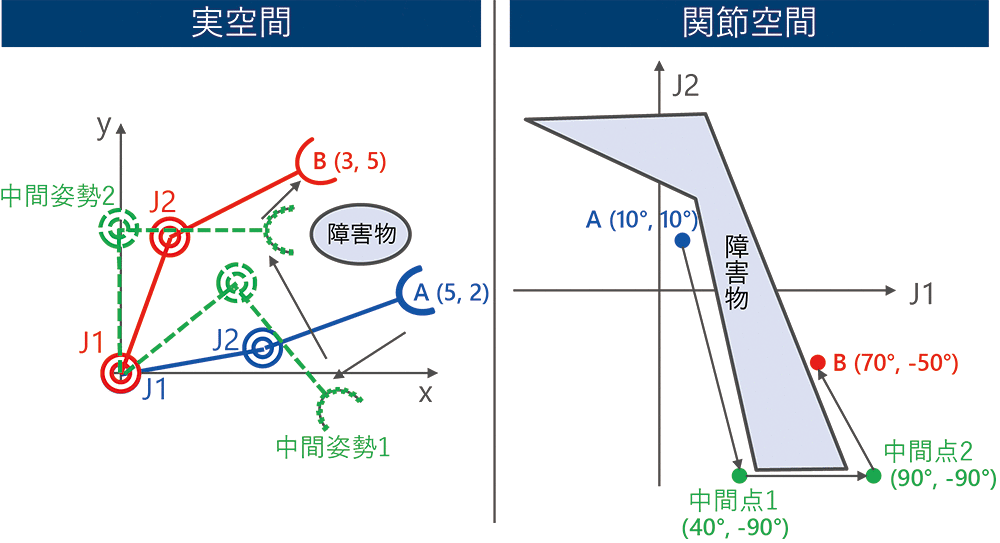
実空間で開始姿勢Aから障害物を回避しつつ目標姿勢Bにロボットを動かそうとした場合、干渉を避けるため中間姿勢1,2を経由する必要がある。中間姿勢の実空間上の位置を人は直感的にあたりをつけることができるが、ロボットを制御するための関節角度に変換するのは容易ではない。TPには直交ジョグ操作というロボットの手先を実空間の座標で並行移動させる機能があり、ある程度は人の感覚に合わせた操作も可能である。しかし、直交ジョグ操作による手先の移動はロボットコントローラが各関節の動きを制御することによって実現されるため、ユーザーはロボットの手先以外の部分(肘・肩)がどのように動くかは制御できない。そのため、直交ジョグ操作だけでティーチングしようとしても、ロボットと周辺環境が干渉する危険がある。また、実空間と関節空間は非線形な関係にあるため、実空間では連続であっても、関節空間では不連続になる領域が存在する。そのような領域ではロボットコントローラで計算する関節値が不定となり、冗長な動作が発生したりロボットが停止したりするため、直交ジョグ操作で長い距離を動かしてもユーザーが望むような動きは得られないことが多い。そのため、実際のティーチングでは関節の回転角度を試行錯誤しながら所望の教示点に近い姿勢まで変化させ、直交ジョグ操作で精密な位置合わせを行うという作業をすることになる。
以上から、現状のロボットのティーチングは熟練者が勘と経験に基づいてトライアンドエラーを繰り返して作業する必要があり、ユーザーにとって非常に負担の大きいものであると言える。
2.3 軌道生成の課題
ロボットを生産設備として使用するには、ティーチングで生成した経路をユーザーが求めるタクトタイムを満たす時間で実行できなければならない。そのためには、経路上の中間姿勢間の関節の回転速度を調整して、高速な軌道を生成する必要がある。
ロボットの関節回転速度は速度最大値と加速度のパラメータによって制御される。基本的にはこれらを大きな値にすれば動作は速くなるが、過大なパラメータを与えた場合は関節のサーボモータにかかるトルク負荷が高くなり、安全装置が動作してロボットが停止してしまうので、適切な値を設定する必要がある。
トルクは以下の式(1)で示されるように、質量や慣性の影響を受けるため、最適なパラメータを求めるためにはロボットに取り付けられたハンドやハンドでつかんだワークの質量や姿勢まで考慮しなければならない。

-
:負荷(トルク)
-
(
) :質量に関する行列
-
(
,
) :遠心力やコリオリ力の項を示すベクトル
-
(
) :摩擦力の項を示すベクトル
-
(
) :重力項を示すベクトル
そのため、ユーザーは推奨値でタクトタイムが満たされない場合は実機を動かしながら試行錯誤してパラメータを調整する必要がある。これはティーチング同様、熟練が必要で時間のかかる作業、すなわちユーザーにとって負担の大きい作業であり、課題となっている。
また、別の課題として、短いタクトタイムを達成しようとするならば、動作パラメータだけでなく経路の再調整が必要になることがある。例えば、腕を伸ばした姿勢で動かすよりも、いったん腕を縮めてから動かしたほうが関節にかかる負荷が小さくなり、より高速に動作させることでトータルの動作時間が短くなるようなケースが存在する。
以上から、ロボットで高い生産性を実現する軌道を生成するには、動作パラメータと経路の両方を試行錯誤で調整するという課題が存在する。
2.4 技術開発目標と評価環境
ロボット動作生成の課題を解決するため、経路の自動生成技術と動作の自動高速化技術を開発した。開発技術の特色は1動作当たり100msecという計算時間の高速性にある。この高速性により、本技術は幅広いアプリケーションへの対応が可能である。
現在、産業用ロボットは、動作の繰り返し精度の高さを生かして、高精度に位置決めされたワークをティーチングされた固定の動作で搬送するような使われ方が主流である。しかし、ばら積みされたワークのピッキングのように事前に動作の条件が固定できないアプリケーションに関しては、ティーチングで対応するには膨大な動作パターンを登録しておいて条件分岐で対応する必要があり、ロボットの適用が困難であるという課題がある。一方、本技術はロボットの動作と並行して次の動作を生成するのに十分な高速性を実現しているため、3Dセンサや認識技術との連携により、この課題を解決できる。つまり、本技術は現在人手で行われているティーチングを自動で行うようにできるだけではなく、ティーチングでは対応が困難だったアプリケーションにもロボットを使用できるようにできるものであると言える。
100msecという目標値は、図3に示すようにばら積みピッキングをターゲットとして設定した。
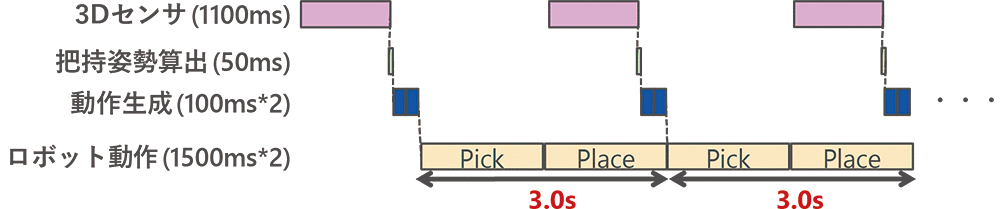
ワークを認識する3Dセンサは、ばら積みの上方に固定する方式とロボットの手先に設置する方式の2通りが考えられるが、本研究では撮影のための動作が不要でより高速な作業が可能な前者の方式を前提とする。
ばら積みピッキングは、ばら積みされたワークを取り出すPick動作と、取り出したワークを整列させるPlace動作で構成される。人同等の作業時間を目標とすると、1ワークあたり3~4secで実行する必要がある。自動でピッキングを行うためには、3Dセンサでばら積みされたワークを計測・認識した後、ピッキングするワークの選定とワークのつかみ方の決定(把持姿勢算出)を行い、Pick動作とPlace動作を生成する必要がある。しかし、Pick動作中は上方に設置されたセンサとばら積みワークの間にロボットが存在してセンサからワークが見えなくなってしまう。そのため、計測からPick/Place動作の生成までの処理は、Place動作の1.5sec中にすべて処理が完了していなければならない。開発目標設定時点では、当時最新のロボット用3Dセンサによる計測・認識には1100msec、オムロンで開発中の把持姿勢算出技術には50msecかかっていた。そのため、動作生成に使える時間はPickとPlaceの2動作で350msecとなる。さらに、通信その他のオーバーヘッドを鑑みて1動作あたり100msecと設定した。
3.経路の自動生成技術
3.1 関連研究
ロボットの経路や軌道を自動生成する技術は、経路計画(Path Planning)・軌道計画(Trajectory Planning)技術と呼ばれ、多くの研究が存在する2)。古典的にはポテンシャル法3)・セル分割法4)などの手法があり、最近ではランダムサンプリング法5,6,7,8,9)や最適化問題として解く手法10,11,12)が存在する。古典的手法は実空間をベースにロボットの通過可能な空間位置を探索してから対応するロボットの経路に変換するもので、探索や変換処理の計算コストが高いほか、実空間と関節空間の非線形性により実行不可能な不連続解を生成してしまう問題がある。ランダムサンプリング法は計算コストが低く、理論上は必ず解を生成するという利点があるが、与えられた状況によって計算時間や生成される経路が大きくばらつくという問題がある。最適化手法は計算時間が安定しており、設定されたコストに応じて最適な経路を生成するが、ランダムサンプリング法と比較して計算時間は長く、経路の生成に失敗する可能性もある。
3.2 既存技術の評価と問題分析
本研究では、計算コストの低さと経路の生成可能性の高さからランダムサンプリング法に分類される手法が有望だと考えた。
ランダムサンプリング方式を、最も基本的なアルゴリアズムであるRRT(Rapidly-exploring Random Trees)5)を例に説明する。RRTは図4に示すように、開始姿勢

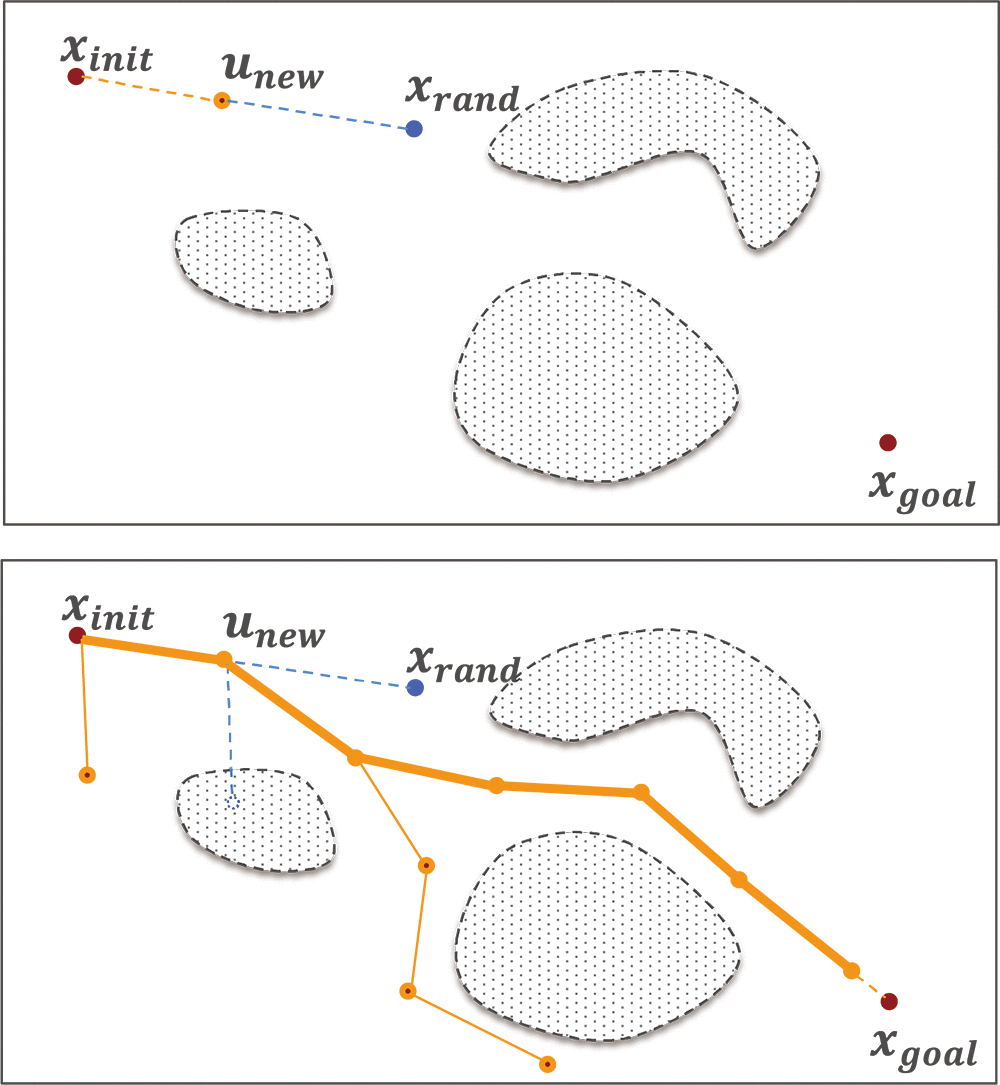
探索は関節空間で行うので、図中の点はロボットの姿勢に対応するベクトルとなる。6つの関節を持つ垂直多関節ロボットならば、関節空間およびベクトルは6次元である。探索は次の手順で行う。ランダムな点












既存研究の中で評価の高いアルゴリズムを選択して評価する。選択したアルゴリズムと概要を表1に示す。
| アルゴリズム | 概要 |
|---|---|
| RRT5) | 図4で説明した手法。評価で用いた実装では5%の確率で をサンプリング点に含めてバイアスを掛けている。 をサンプリング点に含めてバイアスを掛けている。 |
| RRT-Connect7) |  と と の両方からツリーを生成し、他方のツリーの存在する方向に探索することで、障害物の少ないエリアの探索効率を向上する。 の両方からツリーを生成し、他方のツリーの存在する方向に探索することで、障害物の少ないエリアの探索効率を向上する。 |
| TRRT (Transition-based RRT)8) |
 ・ ・ がともに障害物から閾値以下の距離にある場合は がともに障害物から閾値以下の距離にある場合は をツリーに追加しないことで、障害物とツリーが近接することによる成長の阻害を防ぐ。 をツリーに追加しないことで、障害物とツリーが近接することによる成長の阻害を防ぐ。 |
| BIT* (Batch Informed Trees Star9) |
 と と を包含する部分空間を設定してその内部だけを探索することで、探索効率を向上する。 を包含する部分空間を設定してその内部だけを探索することで、探索効率を向上する。 |
評価は図5の条件で開始姿勢から目標姿勢の間の経路を生成させ、計算時間と成功率を計測する。
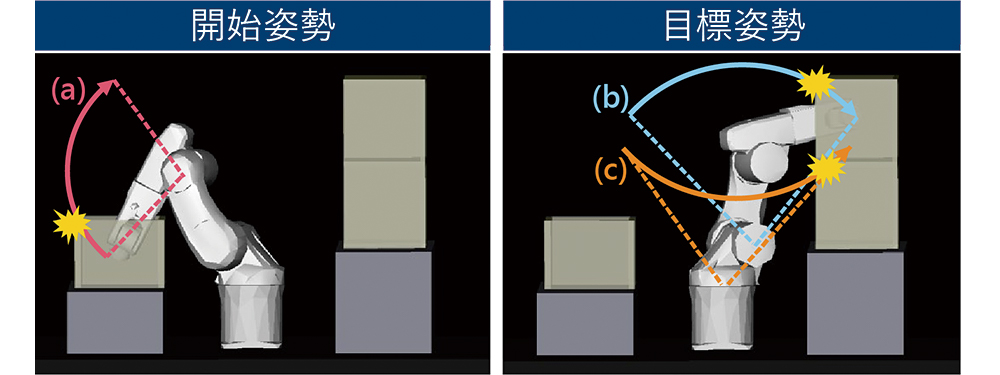
垂直多関節ロボットの第1~3軸は手先の空間位置を変化させ、第4~6軸は手先の向き・傾きを変化させる。つまり、ロボットの動作はほぼ第1~3軸によって決定される。そこで、開始姿勢から目標姿勢の間に第1軸(図5(c))・2軸(図5(b))・第3軸(図5(a))によるロボットの動作をそれぞれ阻害するように障害物を配置した。この条件下でも経路が生成できるのであれば、第1~3軸のどの軸の動作が阻害されても対応可能な、ロボット動作に対して汎用性の高い経路計画アルゴリズムであると言える。なお、計算時間目標に設定したばら積みピッキングの動作としては図5(a)の障害物が回避できれば十分であるが、ばら積みピッキング以外の汎用的な動作生成への適用を考えてこのような条件を設定した。
評価はIntel(R)Core(TM)i5-4310U @2.0GHzのCPUを搭載した計算機で行った。ランダム探索の特性上、計算時間の上限を10秒に設定し、経路生成100回の成功率と成功したときの計算時間を計測した(表2)。その結果、経路生成の成功率はいずれの手法も90%以上と高くなったが、計算時間については100msec以内という目標に対して、大幅に超過した。
| アルゴリズム | 計算時間(msec) | 成功率(%) | |
|---|---|---|---|
| 平均 | 最大 | ||
| RRT | 826 | 2086 | 97 |
| RRT-Connect | 761 | 1629 | 99 |
| TRRT | 892 | 2047 | 94 |
| BIT* | 696 | 2115 | 100 |
アルゴリズム改善のため、ランダムサンプリング方式の問題分析を行った。ランダムサンプリング方式の計算時間

-
:目標姿勢に到達するまでのサンプリング回数
-
:サンプリング点生成にかかる時間
-
:サンプリング点の近傍点探索時間
-
:追加する点と近傍点の距離
-
:干渉判定する間隔
-
:干渉判定1回あたりの時間
したがって、計算時間を短くするには、目標姿勢に到達するまでのサンプリング回数を減らすことと、1回あたりの計算時間を減らすことが必要である。なお、表2で示した実験結果では、サンプリング回数
3.3 探索アルゴリズム改善
既存のアルゴリズムの探索処理を分析したところ、コンテナや棚への出入り部分でサンプリング回数
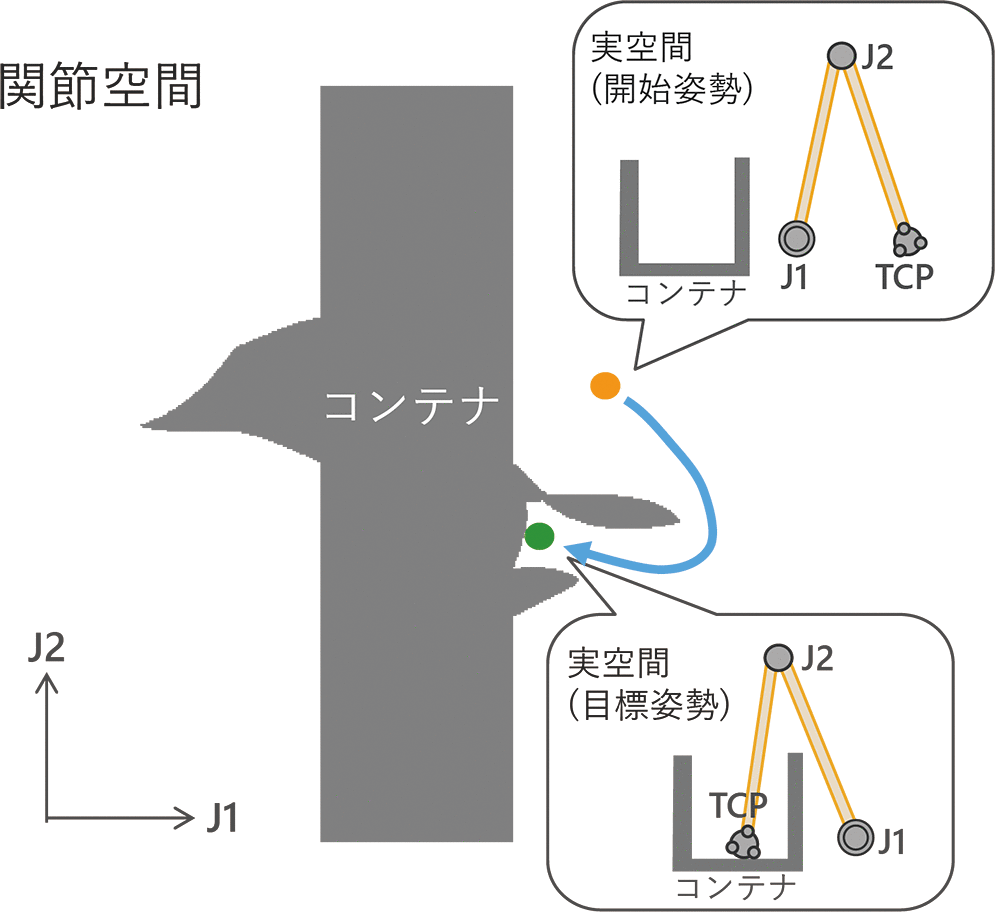
このような問題に対応する手法としては、実空間の情報を使って探索する手法が知られている。代表的なアルゴリズムとしては、実空間で仮想の球を使って探索し関節空間に結果をフィードバックするEET14)がある。この方法は実空間の障害物から離れる方向に向けて探索するので、Bug-Trapの出入り部分に関しての探索性能は高いが、Bug-Trapでないエリアに関しては探索の手掛かりが無くなるため著しく性能が悪化する。一方、表2で評価したアルゴリズムのうち、RRT-ConnectはBug-Trapでないエリアに関して高いパフォーマンスを発揮する。これは、探索範囲に障害物が少ないエリアがあることを期待して設計されたアルゴリズムであり、開始姿勢と目標姿勢の両方からツリーを生成し、他方のツリーの存在する方向に探索するという方針をとっている。そのため、障害物が少ないエリアでは2つのツリーがすぐにつながるため、探索性能が高い。
そこで、これら2つのアルゴリズムを併用するアルゴリズムを新たに考案した。すなわち、Bug-Trap状態にあると判断された場合はEETを使用し、そうでないときはRRTConnectを使用して経路を生成する。なお、図5の例ではロボットの手先とコンテナによるBug-Trapの発生を示したが、これ以外にもジョイント値の上限や、手先以外の部分と障害物の干渉の発生によるBug-Trapも存在するので、考案したアルゴリズムではこれらすべてのBug-Trapの発生要因をチェックしている。
探索アルゴリズムの改善により、サンプリング回数
3.4 干渉判定処理改善
次に、サンプリング1回あたりの計算時間を短くする。計算時間のプロファイル分析を行った結果、干渉判定にかかる時間が処理の9割ほどを占めることが分かった。そこで、干渉判定にかかる時間(


干渉判定はロボットと周辺障害物のCADデータを使った3Dシミュレーションによって行われている。一般的には、式(2)で示した通り経路上の中間姿勢間の関節角度の変化



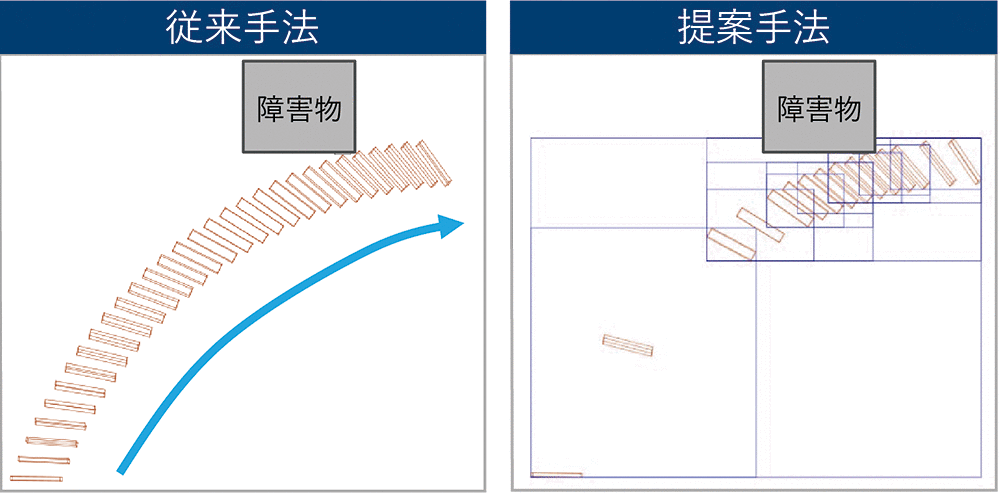
この手法により、干渉判定の正確性を保ったまま、判定回数

さらに、干渉判定1回あたりの計算時間

以上の干渉判定の粗密探索とモデルの簡易化により、サンプリング一回当たりの計算時間を0.05msec以下にすることができた。
3.5 経路自動生成技術の評価
開発した探索アルゴリズムと干渉判定処理を反映して、表2と同じ条件で評価した結果を表3示す。RRT-Connectは表2の結果の転記である。
| アルゴリズム | 計算時間(msec) | 成功率(%) | |
|---|---|---|---|
| 平均 | 最大 | ||
| 開発手法 | 28.9 | 90.4 | 100 |
| RRT-Connect | 761 | 1629 | 99 |
以上から、探索アルゴリズムによるサンプリング回数の削減と、干渉判定処理の高速化により、目標である100msecの計算時間を達成できた。
4.動作の自動高速化技術
4.1 関連研究
ロボットの動作時間を短くするためには、生成する経路の冗長性をなくすことと、動作パラメータを適切に設定する必要がある。そのような技術としては、経路の自動生成技術の関連研究でも触れた軌道計画技術が存在する。軌道計画技術はロボットの経路のほか、ロボットと障害物の距離・手先の向き・関節にかかるトルクをコスト関数のパラメータとして最適化する技術である。この種の技術で有名なものとしてはSTOMP(Stochastic Trajectory Optimization for Motion Planning)11)やTrajOpt(Trajectory Optimization for Motion Planning)12)がある。STOMPは最適化して得られた結果にランダムなノイズを付加して計算することで局所解への収束を抑制して最適解の探索を効率化する、TrajOpt は逐次的に凸最適化を行うことで計算時間を短くする、という特徴がある。しかし、事前の評価によりこれらの効率の良い手法を用いたとしても計算時間が数秒から数十秒かかり、開発目標の100msecには適さないことが分かった。さらに、これらの手法は事前に中間姿勢の点数を決めておく必要があり、その点数が少なすぎれば解を生成できる可能性が低くなり、多すぎれば生成される動作の加減速が多発して動作時間が長くなってしまうという問題もある。
このように、経路の生成・最適化と動作パラメータの最適化を一つの最適化問題として解くと、トレードオフ関係にある多数のパラメータの収束に時間がかかり、設定も複雑になってしまう。そこで、本研究では経路生成技術で生成された経路をベースに、動作パラメータをいったん最適化し、その後で、動作速度に悪影響のある部分を補正するという手順にすることで、高速な動作パラメータ最適化技術を実現した。
4.2 動作パラメータの最適化
ロボットを高速に動作させるためには、速度






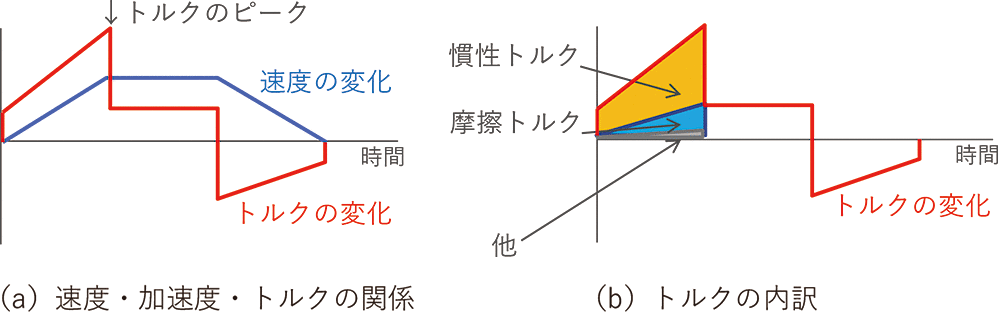
以上から、一般にされているように速度を調整するのではなく、加速度を調整する方が効果は高いことが分かる。そこで、本研究ではロボットの速度はユーザー指定の任意の値かロボット仕様値の最大値のどちらかに固定し、加速度を調整してロボットの動作を高速化させることとした。加速度は以下の手順で調整する。
- 1.
- 経路・与えられた最大速度・ロボット仕様の加速度の50%の値を使って軌道を生成し、1msecごとに離散化して各関節にかかるトルクを計算する
- 2.
- 算出した各関節のトルクの時系列データから関節ごとにピークを抽出し、ピーク位置でのトルクとトルクリミットの差が閾値以下で、かつすべての関節がトルクリミットを超えていなければその加速度を最適値として設定する
- 3.
- ピークトルクがトルクリミットを超過または差が閾値よりも大きい場合は、二分探索で条件を満たす値になるまで加速度を調整し、1.に戻る
4.3 経路の補正
加速度パラメータでロボットの動作を高速化することを考えたとき、慣性トルク






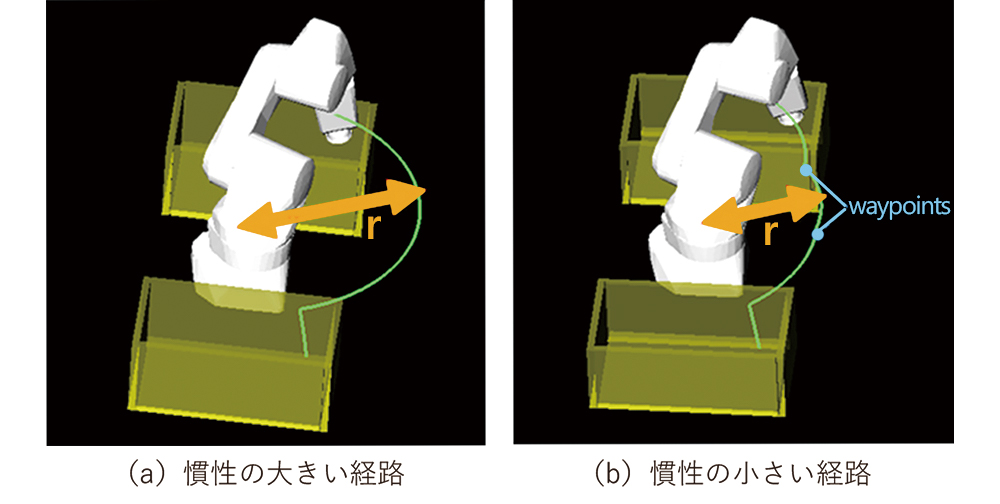
慣性が大きくなるような経路になっていた場合、動作時間が長くならない範囲でロボットの姿勢を慣性が小さくなるように補正することができれば、加速度をさらに大きくすることができる。しかし、経路のすべての区間・すべての関節に対して変更可能かどうかを評価するのは、関連研究で挙げた最適化問題として解く手法と同様の処理となり、計算時間が長くなる。
そこで、関節第1軸に着目して探索範囲を限定し、経路を変更する部分を第2・3軸に限定することで、短時間で補正可能な部分を特定する。第1軸に着目する理由は、垂直多関節ロボットでは根元に近い軸にかかる慣性ほど低減の効果が高いからである。また、変更を第2・3軸にのみ限定するのは、第1軸にかかる慣性は第2・3軸の影響が大部分であるのが理由である。以下に補正方法を説明する。
まず、経路上で第1軸に律速している連続した区間を補正対象区間として抽出する。抽出した区間のうち、第1軸の変化量が十分に長く、区間の中央に第2・3軸を動かして腕を折りたたむ中間点を追加しても動作の減速が発生しないエリアを軌道データから抽出する。そして、第2・3軸をいったん折りたたんでから元の状態に戻すのにかかる時間が、第1軸が補正区間を動くのにかかる時間を超えないように第2・3軸の変化量を設定する。以上の方法で、慣性が小さくなるように経路を補正できる。なお、第1軸に律速する区間とは経路上の隣り合った中間点間において、関節ごとの変化にかかる時間で第1軸の時間が最大になっている区間のことである。
4.4 ロボット動作高速化の効果
動作パラメータの最適化による加速度の最大化と経路の補正による慣性の最小化を交互に繰り返すことで、ロボット動作を限界まで高速化できる。以下に、評価結果を示す。実験ケースは図11に示すような、ロボットの第1軸が180°動きつつ、コンテナから手先を出し入れする動作5パターンで、動作高速化技術を適用する前後の動作時間を比較した。
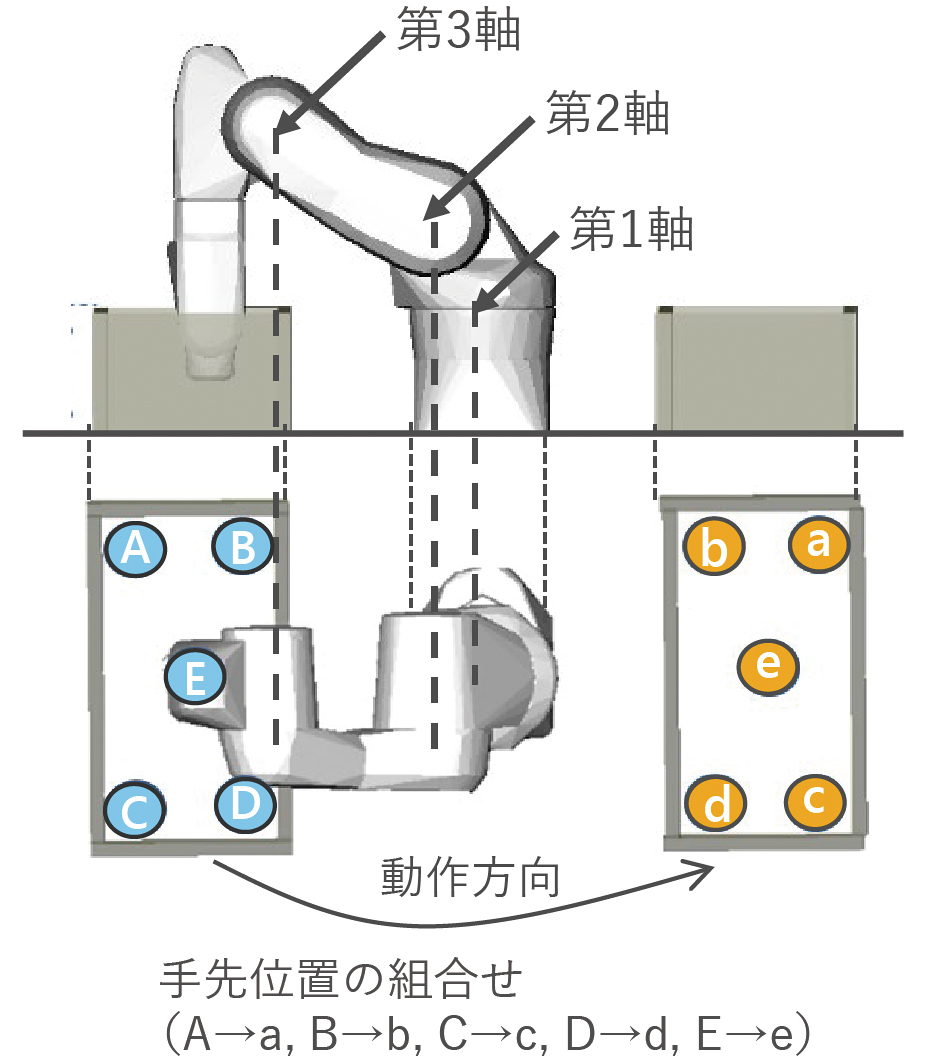
動作時間の比較の際は、ロボット実機動作のばらつきの影響を小さくするため、高速化適用前後の動作をそれぞれ1000回実行して各回の動作時間を計測し、高速化前の動作時間は1000回のうちの最小値、高速化後の動作時間は最大値を使って評価した。また、経路の算出と動作最適の計算は経路計画の評価と同じ計算機で行っている。表4に動作時間の高速化比率と経路計画を含む計算時間を示す。
| 実験ケース | 高速化比率(%) | 最大計算時間(msec) |
|---|---|---|
| A → a | 24.7 | 95.1 |
| B → b | 19.4 | 97.1 |
| C → c | 28.1 | 96.5 |
| D → d | 28.3 | 85.3 |
| E → e | 23.3 | 90.0 |
以上から、100msec以下の計算時間で動作時間を約20%高速化できていることが確認できた。
5.実装したデモシステム
5.1 システム概要
本研究で開発したロボット動作自動生成技術と3Dセンサを組み合わせてばら積みピッキングのデモシステムを開発した。ロボットはオムロンのViper650、センサと認識処理は開発目標の見積もりに使用したロボット用3Dセンサを使用している。図12にデモシステムの外観を示す。

デモシステムでは、ユーザーがGUIから所定のデータを登録することで、ティーチングやパラメータ調整を行うことなくピッキングアプリケーションを実現できる。登録の必要なデータは以下のものである。
- センサ位置
- ばら積みトレイの位置
- 整列トレイの位置
- 整列する座標情報
- ピッキングするワークのCAD形状
- ロボットハンドの形状・仕様
これらは設備の設計で必要なデータのみであり、ロボットの動作生成のための特別なデータは必要ない。
5.2 性能評価
デモシステムで6種類の電子部品のばら積みピッキングをしたタクトタイムを評価した。タクトタイムは図3で示したPick動作とPlace動作のペアを実行するのにかかる時間20回を平均したもので、初回のセンシングから動作生成の時間は評価に含めない。評価結果を表5に示す。
| ワーク(寸法、cm) | タクトタイム(sec) |
|---|---|
| A(2×3×1) | 2.9 |
| B(3×3×2) | 2.7 |
| C(15×1×0.5) | 2.9 |
| D(1×1×1) | 2.9 |
| E(1×0.5×1) | 2.9 |
| F(1×1×0.5) | 3.0 |
この結果は、センシングから動作生成にかかる時間はすべてPlace動作中に完了することで達成されており、計算処理のためのロボット停止は発生していない。以上から、デモシステムが人同等のタクトタイムでピッキングできていることが確認できた。
6. むすび
本研究では、ロボットの生産現場への普及を妨げている要因の一つである、垂直多関節ロボットの動作生成の困難さという問題の解決に取り組んだ。開発した技術はロボットの位置姿勢の設定と動作パラメータ調整を自動で行うロボット動作自動生成技術である。前者は状況に応じたアルゴリズムの選択と干渉判定処理の効率化により短時間での動作生成を実現した。後者はロボットの動作時間に対して効果の高い加速度パラメータを最適化することと、慣性を軽減するように経路を補正することを繰り返し実行することで、ロボットの動作を限界まで高速化することができる。これらの技術は高速に処理可能なので、大量のティーチングが必要なばら積みピッキングにも対応でき、構築したばら積みピッキングのデモシステムでは人と同等のタクトタイムを実現した。開発成果は、ばら積みピッキングアプリケーションやロボットティーチングツールとして商品化の見込みである。
今後は、より複雑なロボットシステムにも対応できるよう、複数台のロボットの同時・協調動作の自動生成への拡張を検討している。
謝辞
本論文の成果は、2016年から2019年にかけての研究開発をまとめたものである。
執筆者のほかに本研究開発に尽力した中島茜氏、森谷俊洋氏、殿谷徳和氏、鈴村章洋氏、倉谷僚一氏に深く感謝申し上げる。
また、本研究の要件設定と商品化検証にご協力いただいたOMRON Research Center of America及びOMRON Robotics and Safety Technologies, Inc.のメンバに感謝申し上げる。
参考文献
- 1)
- 近畿経済産業局.“平成27年度「 産業用ロボットの新分野展開における導入阻害要因調査」”.経済産業省.2016-05-31.https://www.kansai.meti.go.jp/3jisedai/report/report2015.html,(参照 2020-11-16).
- 2)
- 比留川博久.経路探索問題―ロボットの動作計画―.情報処理.1994, Vol.35, No.8, p.751-760.
- 3)
- Loeff, L. A. Algorithm for Computer Guidance of a Manipulator in Between Obstacles. Diss. Oklahoma State University, 1973.
- 4)
- Schwartz, J. T.; Sharir, M. On the “piano movers” problem. II. General techniques for computing topological properties of real algebraic manifolds. Advances in Applied Mathematics. 1983, Vol.4, No.3, p.298-351.
- 5)
- LaValle, S. M. Rapidly-exploring random trees: A new tool for path planning. Computer Science Dept. Oct. 1998, Vol.98, No.11.
- 6)
- LaValle, S. M.; Yakey, J. H.; Kavraki, L. E. “A probabilistic roadmap approach for systems with closed kinematic chains”. Proceedings of 1999 IEEE International Conference on Robotics and Automation(Cat. No. 99CH36288C). 1999, Vol.3. p.1671-1676.
- 7)
- Kuffner, J. J.; LaValle, S. M. “RRT-connect: An efficient approach to single-query path planning”. Proceedings of 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065)IEEE, 2000, p. 995-1001.
- 8)
- Jaillet, L.; Cortés, J.; Siméon, T. “Transition-based RRT for path planning in continuous cost spaces”. 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2008, p.2145-2150.
- 9)
- Gammell, J. D.; Srinivasa, S. S.; Barfoot, T. D. “Batch informed trees(BIT*): Sampling-based optimal planning via the heuristically guided search of implicit random geometric graphs”. 2015 IEEE International Conference on Robotics and Automation. IEEE, 2015, p.3067-3074.
- 10)
- Ratliff, N., et al. “CHOMP: Gradient optimization techniques for efficient motion planning”. 2009 IEEE International Conference on Robotics and Automation. 2009, p. 489-494.
- 11)
- Kalakrishnan, M., et al. “STOMP: Stochastic trajectory optimization for motion planning”. 2011 IEEE International Conference on Robotics and Automation. IEEE, 2011, p.4569-4574.
- 12)
- Schulman, J.; Ho, J.; Lee, A. X.; Awwal, I.; Bradlow, H.; Abbeel, P. Finding Locally Optimal, Collision-Free Trajectories with Sequential Convex Optimization. Robotics: Science and Systems. 2013, Vol.9, No.1, p.1-10.
- 13)
- LaValle, S. M. PLANNING ALGORITHMS. Cambridge University Press, 2006, 842p., ISBN978-0-52186-205-9.
- 14)
- Rickert, M.; Sieverling, A.; Brock, O. Balancing exploration and exploitation in sampling-based motion planning. IEEE Transactions on Robotics. 2014, Vol.30, No.6, p.1305-1317.
- 15)
- Ericson, C. Real-Time Collision Detection. CRC Press, 2005, 632p., ISBN978-1-55860-732-3.
- 16)
- Gaschler, A.; Fischer, Q.; Knoll, A. The bounding mesh algorithm. Technical Report TUM-I1522, Technische Universität München, 2015.
本文に掲載の商品の名称は、各社が商標としている場合があります。














