商品開発における技術要素間のトレードオフを解消するバランス設計手法の革新
商品開発においては、開発の後工程で不具合が発生すると設計変更が必要となり、開発リードタイムやコストの超過、更には品質の低下を招くことが共通的な問題になっている。発生する不具合は多岐にわたるが、複数の技術要素間のトレードオフが解消しきれないまま、後工程にリスクが持ち込まれることが、主要な原因の1 つとして挙げられる。
本論文では、複数の技術要素間のトレードオフを商品開発の上流で解消するバランス設計手法として、設計最適化手法の活用を検討した。検討においては、実際の設計課題を対象に試行し、CAE と連携したコンピュータによる自動計算により、2 週間で約1800 件の設計案を検証すると共に、これまでの機能特性を超える最適解の抽出を実現した。試行を通じて、バランス設計を実現できる確証を得たことに加えて、従来の勘・コツ・経験ベースの設計では抽出しきれなかった最適解を抽出できる可能性を得た。
1.まえがき
商品開発においては、後工程で不具合が発生すると、設計変更が必要となり、開発リードタイムやコストの超過、更には品質の低下を招くことが共通的な問題になっている。発生する不具合は多岐にわたるが、複数の技術要素間のトレードオフが解消しきれないまま、後工程にリスクが持ち込まれることが、主要な原因の1 つとして挙げられる1)。
この原因の背景には、2 つの点が考えられる。第1 に、近年、商品の高性能化や高機能化が急速に進み、限られた設計自由度の中で、新技術の活用、より詳細なすり合わせといった高度な設計力が必要となっていることである。これまで開発現場では、技術要素別に設計を分業化(例:メカ・エレキ・ソフトなど)し、個々の設計力を洗練化することで対応してきたが、技術要素間のすりあわせが不足しがちになっている1)。
第2 に、商品開発に必要な開発リソース(期間、工数、経費など)の確保が難しくなっていることである。これまでは、人手による設計計算や、実機試作による検証を行っても十分な量の設計検証ができていた。しかし、近年では、検討が必要な技術要素・パラメータの数が膨大になり、従来の設計手法では対応しきれず、設計品質の低下を招く要因にもなっている1)。
近年では、CAE(Computer Aided Engineering の略)などのコンピュータにより設計検証を行う技術が発達している。これらの技術活用により、個々の技術要素の設計に対し、手計算では対応できない複雑な計算を高速に実行すると共に、現物(試作品)が無い中でも検証できるようになってきた。また、世間では、設計者の勘・コツ・経験といった設計知見による製品アイデアの発想や、設計結果の妥当性判断を支援するため、コンピュータにより、個々のCAE 結果を統合して分析し、トレードオフなど多くの設計要件に対する最適な設計値の検証・探索を行う設計手法(以後、設計最適化手法と呼ぶ)の研究も進められている2)。しかし、これらの技術を実際の商品開発で連携させて活用するには、設計者の手作業・判断に依存しているのが現状である。
本論文では、新たな設計手法として、複数の設計要件を満たす設計案(以後、適正解と呼ぶ)を導出するために、設計者に代わりコンピュータがCAE と設計最適化手法を連携して実際の設計問題を解決する新たな設計手法を実践し、従来の設計者主導の設計手法と効率・効果の両面で有効性と、実用化に向けた課題について考察する。
2.設計最適化手法
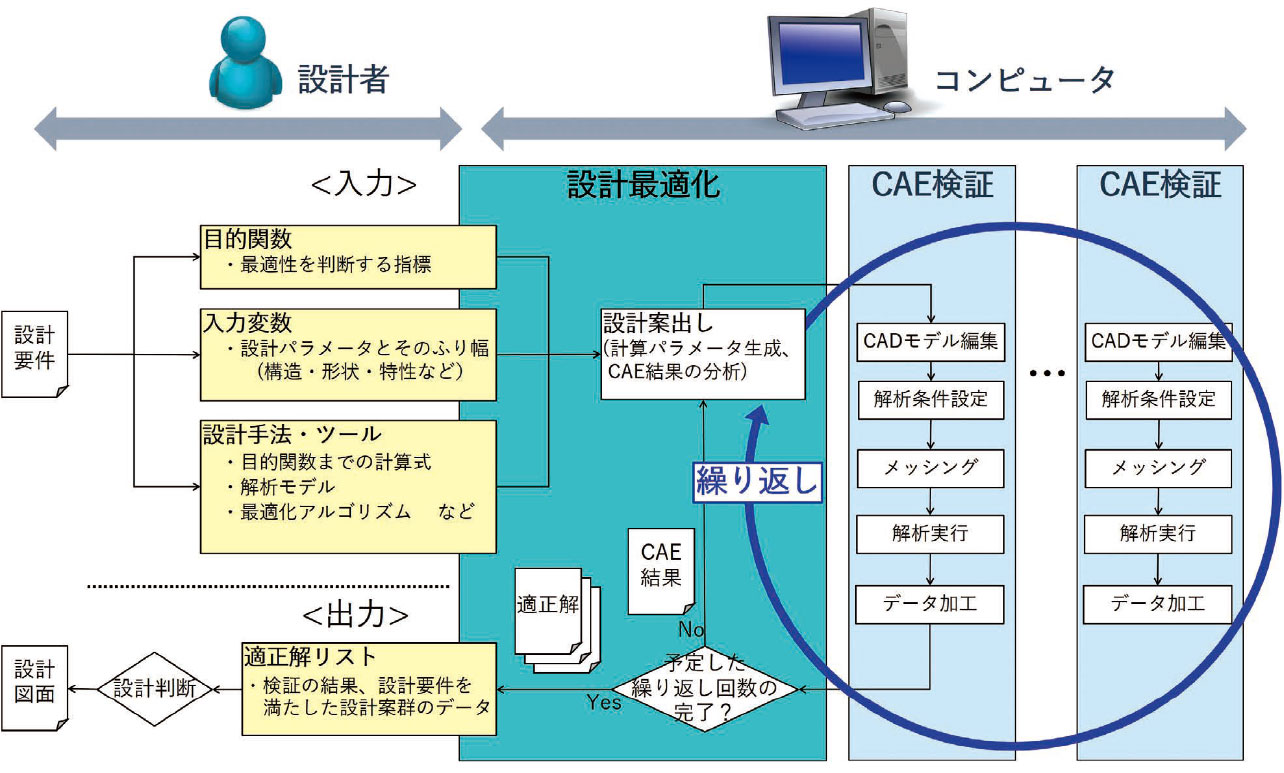
図1 は、本論文で検討した設計最適化手法の全体像である。これまで設計者が行ってきた一連の作業や判断をコンピュータに実行させることを特徴としている。まず、設計者は、与えられた設計要件に対する設計内容として、目的関数、入力変数、および使用する設計手法・ツールをコンピュータに入力する(各語句の説明は、図1 中に記載)。特に、設計手法は、設計者が商品を設計するために行う一連の計算、検証などの作業や、要件に対する合否判定などの判断の工程であり、この工程をコンピュータに行わせるために、図1 右側のようにプログラム化する。
また、本手法における出力は、適正解のリストである。設計者はリストから最も良い設計値(以後、最適解と呼ぶ)を判断・選定する。
本手法で重要なのは、図中に示した「設計案出し」工程と「CAE検証」工程を、コンピュータにより自動的に繰り返し実行させることである。これは、従来、設計者がより良い設計値を追求するために、多くの仮説立案と実験により行ってきた試行錯誤の取り組みに相当する。
2.1 「設計案出し」工程
従来、設計者は、多くの設計経験により培われた設計手法やノウハウを駆使し、設計案の検討を行ってきた。しかし、設計経験が無いコンピュータに設計案を抽出させるには、下記2 つのロジックを与える必要がある。
- 設計範囲の絞り込み
- 最適解の絞り込み
各ロジックの概要と基本的な手法について次に述べる。
2.1.1 設計範囲の絞り込み
商品の設計には、多くの設計パラメータが関与しており、各パラメータには寸法や材料特性などの許容範囲がある。設計とは、許容範囲がある設計パラメータのすべての組み合わせ(以後、設計空間と呼ぶ)から、設計要件を満たす設計値の組み合わせを抽出する行為である。無数の組み合わせがある設計空間から効率よく設計検証を進めるには、まず、設計要件を満たす可能性がある範囲(設計範囲)を抽出する必要である。「設計範囲の絞り込み」とは、そのロジックであり、一般的に実験計画法を用いる。統計的に設計空間を均等に分割し、設計要件に対する特性をサンプリングすることで、設計空間全体の傾向を把握することができる。
<実験計画法の例2)>
一様乱数法、モンテカルロ法、ラテン超方格法など
2.1.2 最適解の絞り込み
抽出した設計範囲内から最適解を追求するロジック(以後、最適化アルゴリズムと呼ぶ)が「最適解の絞り込み」であり、主な手法としては、数理計画法と発見的手法がある1)。
前者は、数学的に解を求める手法である。厳密な解が得られるが、適用する設計内容には、「定式化できる」、「連続的な問題である」、などの制約がある。
一方後者は、サンプリングしたデータから、より良い解になる方向性を統計的に分析し、最適解を追求する手法である。時間的な制約などの影響により解の厳密性が数理計画法よりも低いが、設計内容に対する制約が少ないため汎用性が高い。今回の試行では、多様な技術要素が関わる商品開発への適用を想定し、制約が少ない後者を最適化アルゴリズムとして採用している。
<最適化アルゴリズムの例2)>
- 数理計画法(線形計画法、非線形計画法など)
- 発見的手法(遺伝的アルゴリズム、焼きなまし法など)
2.2 「CAE 検証」工程
図1の「CAE検証」工程の枠中に、CAEを活用した設計検証の概略工程を示す。従来、これらの工程は、設計者の関与(手作業、判断など)によって行われるが、人の作業や思考のスピードに依存するため、限られた時間で多数の設計案を検証するには限界があった。従って、これらの工程を大量に繰り返し実行するには、一連の工程をコンピュータにより自動的に実行させる必要があり、そのためのプログラム(以後、計算プログラムと呼ぶ)を準備する必要がある。具体的には、API (Application Programming Interface の略) など、連携させるツールの機能やデータを外部から使用・操作するためにツール毎に定義されているインタフェースを活用してプログラムを記述する。しかし、このインタフェースは、連携させるツール毎に異なると共に、活用するには高度な知識・スキルが必要であるため、プログラムの準備は容易ではない。そこで、近年の設計最適化ツールでは、主要な市販CAD/CAE ツールに対するインタフェースが予め用意され、計算プログラムが記述しやすくなってきている3)。
3.試行
具体的な実施事例として、リレー開発における設計最適化事例を紹介する。
3.1 適用事例
リレーとは、外部から入力された電気信号に応じて、電気回路のオン/オフを制御する部品である。図2 に、代表的なリレーにおける主要な構成と動作状態を示す。
コイルへの通電が無い状態では、ばねには力が加わらないため、接点は離れている(接点オフ状態(図2a)。次に、コイルへの通電により電磁石が励起すると、発生した電磁力により鉄片が回転変位して可動ばねを押しこみ、2 つの接点は接触する(接点オン状態(図2b)。その後、コイルへの通電が切れるとばねの反力により接点が離れ、接点オフ状態に戻る。電磁力とばね反力のバランスが崩れると、接点オン/接点オフ状態の切り替えがスムーズに行われなくなる。極端な場合、ばね反力が電磁力より強すぎると可動接点が変位しないため、接点オン状態に移行できず、リレーとしての機能が成立しない。このため、2 つの力の最適なバランスの実現が重要な設計要件となる。
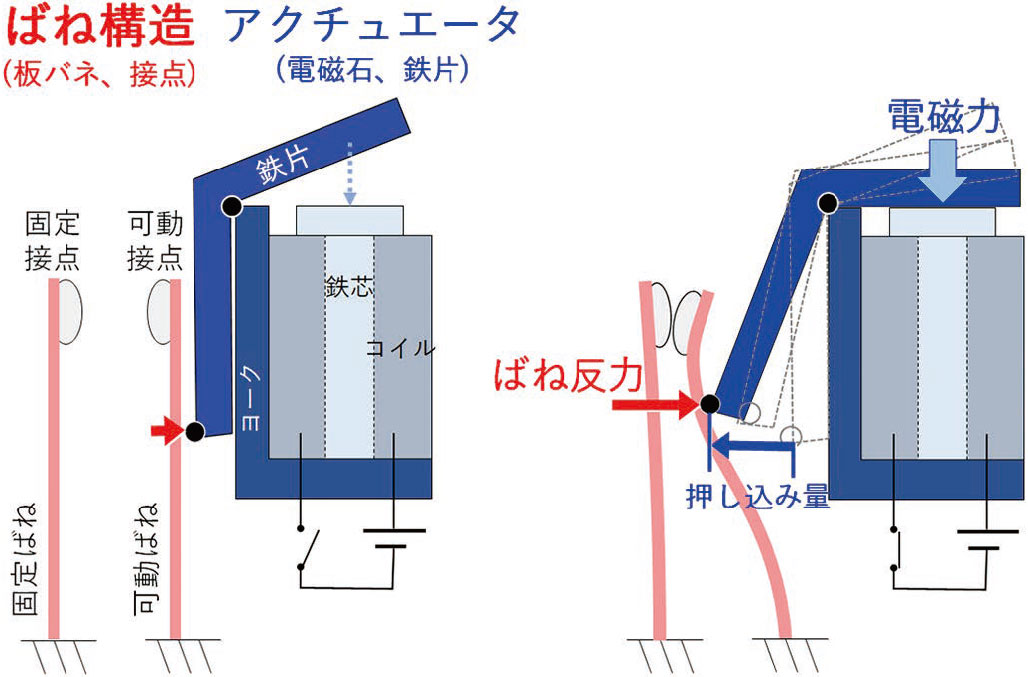
本試行では、アクチュエータの電磁力特性を固定条件とし、最適なバランスを得るためのばね構造の導出に取り組んだ。
3.2 計算プログラム
図3 に、試行に向けて準備した計算プログラムを示す。
3.2.1 最適化条件の記述
まず、最適化を行う条件として、主に、下記4 点について記述した(付記した例は、試行時の内容)。
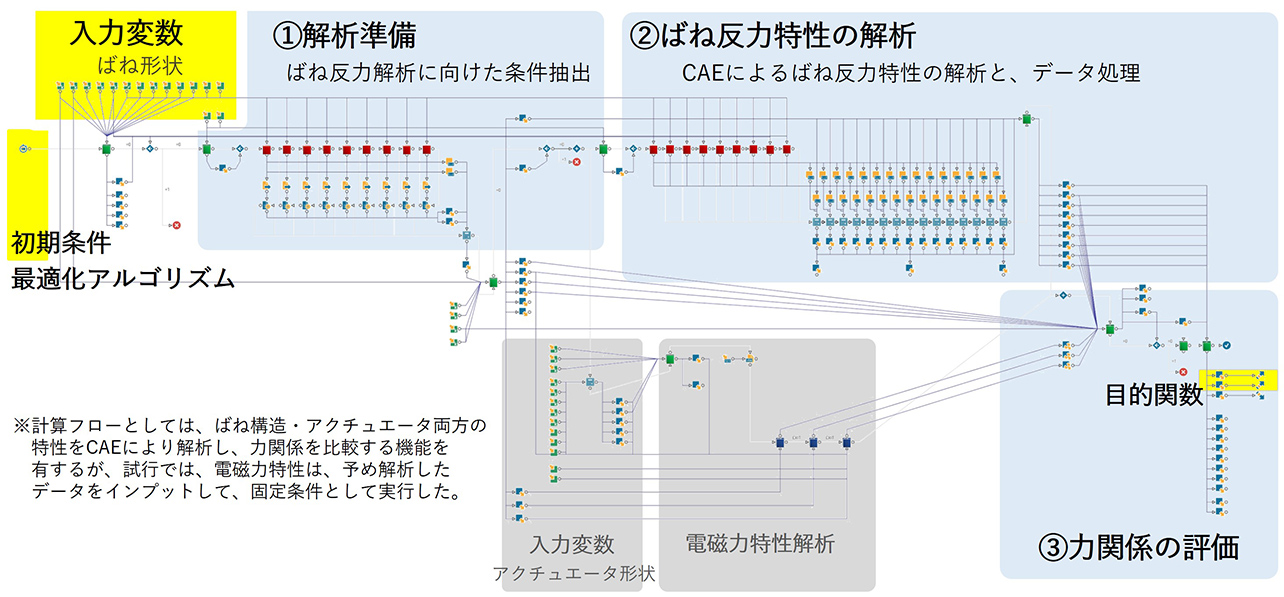
- 初期条件:最適解探索の起点となる設計案
設計空間全体を均等に分割するため、実験計画法として一様乱数法を用いて複数のばね設計案を生成し、入力した。 - 最適化アルゴリズム
適正解が離散的な設計空間や、複数の目的関数に対する設計内容に汎用的に対応させるため、遺伝的アルゴリズム(GA)を使用した4)。 - 入力変数:設計案を構成するパラメータ
ばねの厚み・幅・長さ方向の寸法、アクチュエータの可動ばね押し込み位置などのパラメータを設定した(9 項目)。また、各パラメータに対して、設計上の許容範囲となる最小値-最大値を設定した。 - 目的関数:各設計案の良し悪しを評価する指標・基準
オン/オフ状態のスムーズな切り替えに必要な電磁力とばね反力の力関係(2 項目)を指標とした。
3.2.2 「CAE 検証工程」の記述
今回の試行テーマでは、市販の構造解析CAE ツールと連携してばね反力の解析を行う工程(図中②部)を中心に、解析条件を抽出する工程(図中①部)、解析結果から目的の力関係を評価する工程(図中③部)をタスクや設計パラメータの単位で記述した。記述には、設計最適化ツールで用意されたアイコン化されたインタフェースを用いた。また、従来人手で行ってきた作業や判断については、それぞれ専用のスクリプトやマクロなどを作成し、実装している。
3.3 計算結果
3.3.1 計算工程の実績
本節では、計算とは、図1で示した「設計案出し」、「CAE検証」工程のくりかえしにより、適正解を収集する工程を示す。試行では、実際の開発テーマにおける構想設計段階を想定し、計算期間を2 週間と設定した。
その期間で行った計算の実績を表1 に示す。この期間中に、約1800 件の計算を行い、728 件の適正解を抽出することができた。この工程は、設計案出しの手計算に加えて、CAD モデルの変更などの作業までを含んでおり、全てを実行すると1 日に数件程度しか実行できなかった。工程をすべてコンピュータで自動化したことにより、従来の約180 倍の効率で計算を実行したことになる。
| 計算期間 | 2週間 |
|---|---|
| 計算期間中に検証した設計案数 | 1800件 |
| 抽出した適正解数(設計要件を満たした設計案) | 728件 |
3.3.2 適正解の分析
計算結果(適正解のリスト)から最適解を抽出する工程は、判別指標や基準の妥当性を見極めるため、設計者に依頼した。
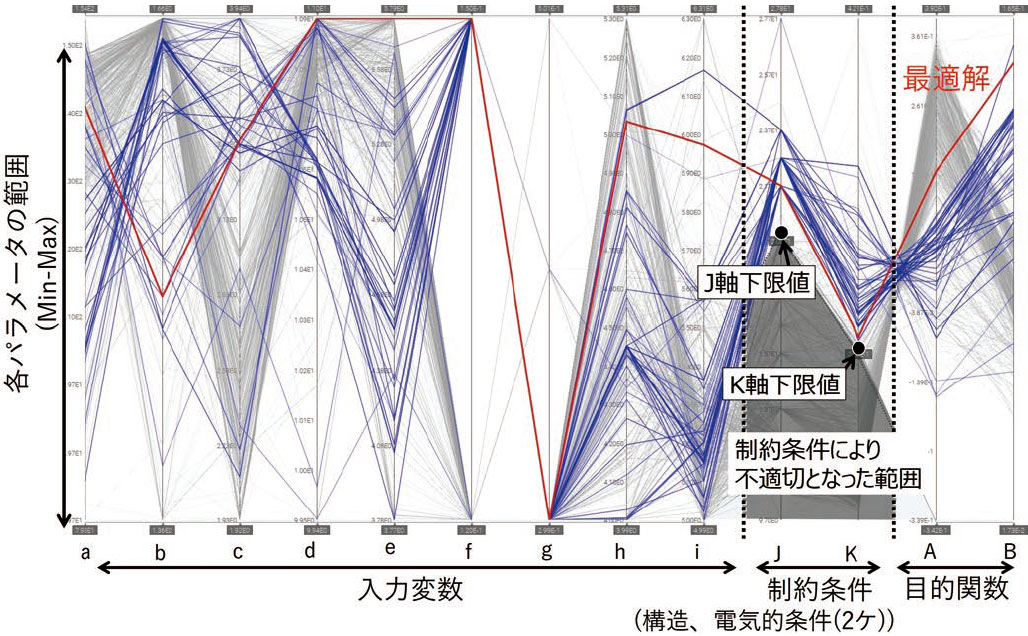
図4 は、計算結果から得られた適正解データの一覧を多次元解析チャートと呼ばれる手法で可視化したものである。図中、各適正解のデータ(9 ケの入力変数値と、その検証結果である2 つの目的関数値)は、横方向に配置した各パラメータ軸上の点をつなぐ折れ線(青線)により、表示している。また、図中、縦軸のレンジは、パラメータ毎の最小値-最大値の範囲である。
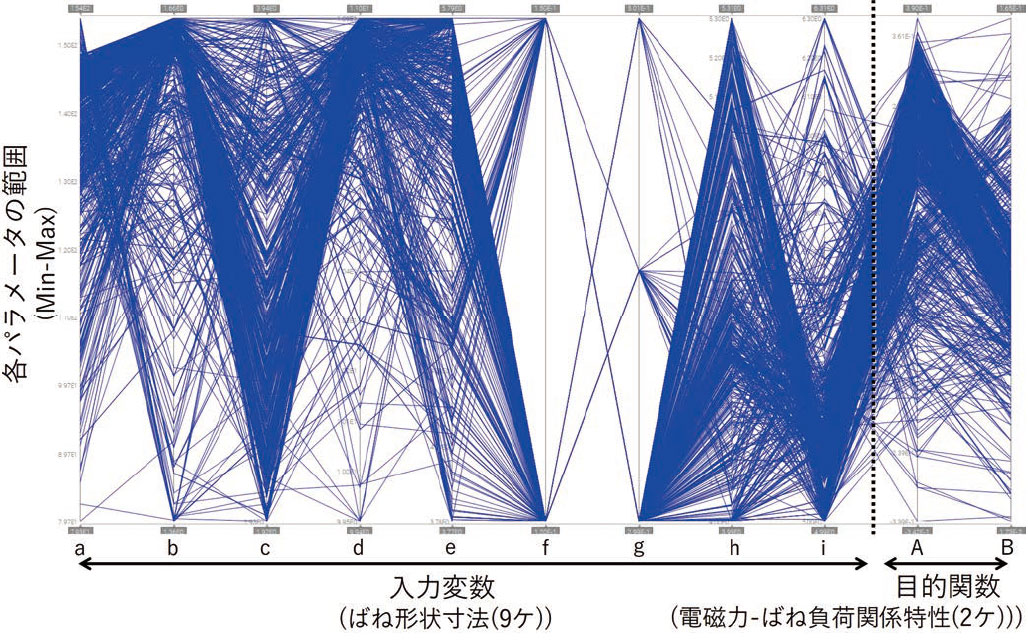
この結果から、入力変数が下記2 つのグループに分かれることが分かった。
- 設計上の自由度が高い入力変数(図中、a~e,h,i)
折れ線が通過した点が各軸のレンジ全体に分布している - 拘束条件となる入力変数(例:f,g)
折れ線の通過点がほぼ限られた値に集中しているパラメータ
3.3.3 最適解探索の履歴
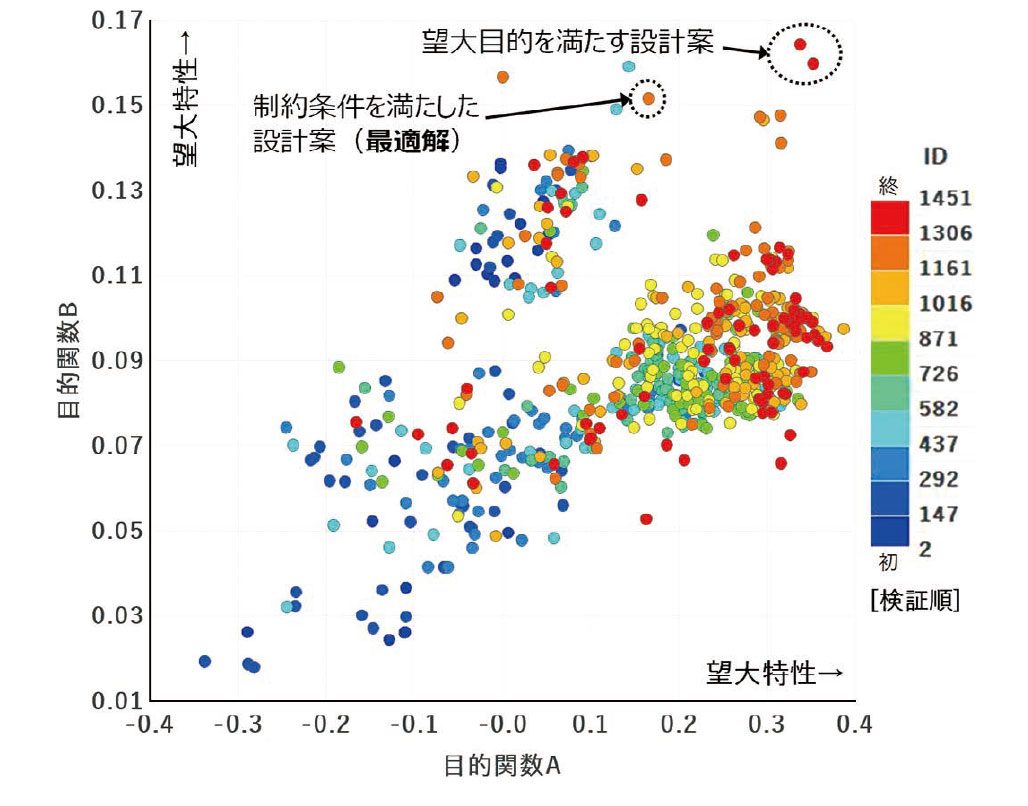
次に、適正解の中から最適解を抽出するために、目的関数A, B をそれぞれX 軸、Y 軸に設定して、適正解リストをプロットしたグラフを図5 に示す。図では、各適正解の点に対し、検証が行われた順で時系列的に、青から赤の順に色付けしている。
試行では、目的関数A, B を最大化することを目的(望大特性)としているため、グラフの右上方向にある点ほど理想的な結果となる。グラフ上の右上方向に向かって赤色の点が増えていることから、最適化アルゴリズムが効果的に作用し、両目的関数の最大化に向け、着実に設計案の探索が行われたことが分かる。
3.4 最適解の抽出
次に、図4、5 を用いて、最適解を抽出した経緯について述べる。
まず、図5 の右上端にある2 点のように、2 つの目的関数が同時に最大になる適正解を最適解の候補として、その妥当性の検証を行った。具体的な観点としては、入力変数値をCAD 上で可視化したばね形状や、可動ばねの変位特性などの挙動が挙げられる。その結果、2 つの構造上および電気的特性(以後、制約条件と呼ぶ)に対する設計要件の不足があることを確認した。これらの制約条件は、従来、設計者が経験を基に判断していた事象であり、熟練者の暗黙知を新たな設計要件として顕在化できた事例でもある。
図6 は、図4 の多次元解析チャートに、顕在化した2 つの制約条件の軸を追加し、適正解の比較評価を行えるように改良ものである。各制約条件軸上に新たな判断基準(今回は、設計者の判断基準として両軸共に下限値)を設定してフィルタリングした結果、図5 で最適解候補とした右上端の2 点を含む多くの適正解が不適切であることが分かった(灰色の折れ線グラフ)。この結果から、フィルタリングの結果で残った適正解(青色の折れ線)の内、目的関数が最大となる設計案(赤色の折れ線)を最適解として選定した。なお、この最適解については実機試作による検証を行い、期待どおりの特性を実現できていることを確認している。
4.考察
実際の設計課題を対象に試行した設計最適化手法について、その効果と、実用面での課題を考察する。
4.1 設計手法の効果
設計最適化手法の活用により、2 つの目的関数に対するトレードオフを解消する最適なばね構造の設計案を抽出することを実現した。また、コンピュータにより算出した結果に頼らず、適正解リストを多次元解析チャートなどの手法で可視化し、設計者視点を加えることで、より実現性の高い解を得たことは価値が高い。
更に、得られた最適解は、設計者が経験上、別の設計要件への影響を懸念して避けてきた形状だったが、実機確認の結果、懸念された設計要件も合わせて改善するものであることが分かった。この結果から、設計最適化手法は、設計空間全体を網羅的に検証することで、論理的に最適値を見出す手法として効果が期待できることを示している。
4.2 実用化に向けた課題
今後の実用化に向けては、より多くの設計要件に対するトレードオフを解消できるようになる必要がある。試行でトレードオフ対象となった目的関数や制約条件は、製品全体に対する設計要件としては、ごく一部である。例えば目的関数が増えると統計上必要なサンプリング数が増え、CAE 検証の繰り返しにかかる時間が増加する。設計最適化手法の実用化に向け、現実的な計算時間で十分な設計検証を行うには、下記のような検討が必要である。
-
CAE 検証時間の削減
-CAD,CAE モデルの簡素化/合理化
-計算インフラの強化 など -
設計要件、設計パラメータの最適化
-検証する技術要素に対する寄与度による設計
パラメータ数の削減
-手戻り規模・頻度などによる設計要件の優先
順位付け など
4.3 設計知見の蓄積に向けた課題
設計最適化手法では、これまで現場で培われてきた設計手法・ノウハウを計算プログラムの形で形式知化できたことが重要な成果である。開発現場の設計者毎の作業、判断の工程や基準を集約して記述できたことで、属人的な設計の質のばらつきを抑えることが期待できる。さらに、3.4 節で追加した制約条件や、4.1 節で発見した従来の設計知見に代わる新たな設計知見のように、設計最適化手法の活用を通じて得られる新たな知見を計算プログラムにフィードバックし続けることで、設計力の継続的な改善が期待できる。
しかし、3.2 節で紹介した計算プログラムを構築するのに、約1 年を要した。主な要因は、下記の2 点である。
- 熟練した設計者の長年の経験の蓄積に基づく感覚的・暗黙的な作業・判断の形式知化
- 活用するCAD・CAE ツールを計算プログラムから自動実行させるためのツール間インタフェースの構築
前者は、近年、社会でも重要な課題として取り上げられ、様々な取り組みが行われているが、まだ明確なソリューションの実現には至っていない。熟練の設計者と連携し、計算プログラムに実装する設計知見を効率的、効果的に収集、加工するしくみ・体制の構築が重要な課題と考える。
また、後者については、今回の試行では、2.2 節で述べた設計最適化ツールで用意されたインタフェースでは対応しきれない設計内容(複雑なモデル形状や、特殊な解析条件など)が多く、技術的に解決するのに時間がかかった。特に、インタフェース構築には、設計最適化・CAD・CAEなど各ツールを高度に使いこなす専門的な知識(例:APIなど)が必要であり、各ツールのベンダとのテクニカルな連携が課題となる。
前記2 つの課題から、設計最適化の実用化には、関係者(開発現場の設計者、設計最適化担当者(計算プログラム構築/運用担当)、各ツールベンダ)が密に連携するしくみやネットワークの構築が重要と考える。
5. むすび
本論文では、商品開発の上流で複数の技術要素間のトレードオフを解消する設計手法の1 つとして、設計最適化手法の活用を検討した。また、試行テーマとして、リレー設計におけるアクチュエータの電磁力とばねの反力のバランス設計を行い、短期間で大量のばね形状の設計、検証を行い、従来の設計知見を超えてトレードオフを解消した最適解を抽出することができた。
今後は、社内の幅広い商品の開発現場に向けて、設計最適化手法の展開を目指す。そのために、多様な技術要素を対象にした設計最適化事例を獲得していく。そして、事例から得られる設計者知見やインタフェース情報を、主要な設計内容ごとに雛形となる計算プログラムを整備することで、効率的な本手法の展開と、設計手戻りのさらなる削減に向けた設計力強化を推進する。
参考文献
- 1)
- 池田義雄.プロントローディングによる上流設計力強化.東芝レビュー.2007, Vol.62, No.9, p.2-8.
- 2)
- 山川 宏,他.最適設計ハンドブック―基礎・戦略・応用―.朝倉書店,2003, 518p.
- 3)
- Esteco SpA. modeFRONTIER ユーザーガイド,2019.
- 4)
- 三宮 信夫,他.遺伝アルゴリズムと最適化.朝倉書店,1998,185p.
本文に掲載の商品の名称は、各社が商標としている場合があります。














