パワーコンディショナにおける系統インピーダンスの影響を打ち消す制御方式の開発
- パワーコンディショナ
- ACリアクトル小型化
- 系統インピーダンス推定方法
- インピーダンス抑制補償器
PCS(Power Conditioning System)の体積とコストを低減させるために、インバータ出力を平滑するACリアクトル(以下ACL)の小型化が検討されている。しかし、PCS-系統間の導線が持つインピーダンス(系統インピーダンス)のリアクタンス成分に対してACLインピーダンス値が小さくなると、制御安定性を損なうという問題が指摘されている。制御設計で安定性改善を試みる例も提案されているが、CPU演算負荷が増加するという懸念がある。本論文では、演算負荷が少ない手法で系統インピーダンスをPCS自身が推定し、最適な制御パラメータを設定する方式を提案する。本方式によりPCS設置後の系統インピーダンスに合わせて安定性を確保できるため、さらなるACLの小型化が可能になる。その結果、PCS全体の小型・ローコスト化に貢献できる。
1. まえがき
1.1 再生可能エネルギーを普及させる意義
エレクトロニクスが発展した私たちの社会において、電気エネルギーは様々な形で利用され、欠かすことのできないエネルギー源である。しかしながら、国際エネルギー機関(IEA: International Energy Agency)の調査によると2015年の全世界発電量の81.4%が石炭、天然ガス、石油による発電となっており、世界規模で枯渇性資源に依存した発電構成となっている 1)。この構成が今後も続くと、社会要求を満たす発電量を維持できなくなることが危惧されている。課題の解決手段として、再生可能エネルギーの利用が検討されている。従来再生可能エネルギーは導入コストが多いことが普及の妨げになっていたが、電力変換器の高効率・小型化によって導入コスト低下が進み、普及が広がっている。持続可能な社会を実現するためには、今後さらなるローコスト化によって再生可能エネルギーの普及拡大が求められる。
1.2 PCSの役割と課題
当社では再生可能エネルギーとして太陽光発電に着目し、PCS(Power Conditioning System)を製品化している。PCSとは、太陽電池によって発電された電気エネルギーを系統電力網で使用されている交流電力に変換し、連系する装置である。図1に太陽光発電用PCSの外観を示す。

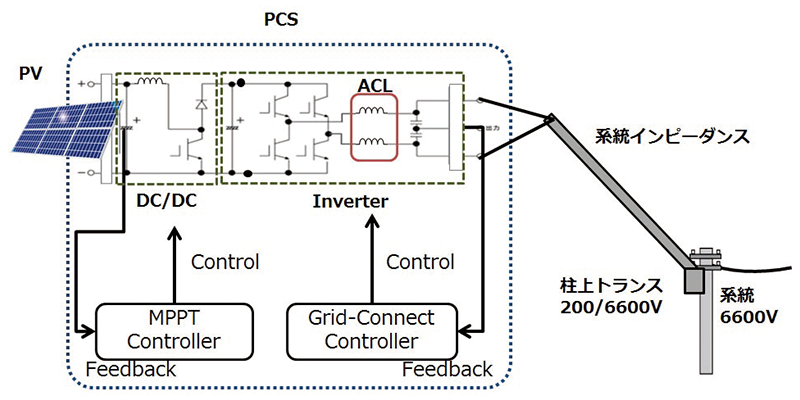
太陽電池を接続したPCS概略図を図2に示す。PCSは前段のDC/DCコンバータと後段のインバータという2つの電力変換器で構成されている。前段は太陽電池からの入力電力を最大電力追従制御(Maximum Power Point Tracking Control)によって常に最大電力となるよう制御して、後段のインバータに送り込む。後段のインバータは直流電力を交流電力に変換し、系統連系制御(Grid-Connect Control)により、系統の変動に追従しながら電力を系統網に送り込む。
これらの電力変換器を構成する部品のうち、コスト・体積をしめる割合が多いのがリアクトルである。特にインバータのLCフィルタに用いられるACリアクトル(以下ACL)を小型化することは、PCS全体の小型・ローコスト化につながる。
しかしながらACLが小さくなると、ACL、LCフィルタキャパシタ(以下ACC)、そして系統-PCS間の導線が持つインピーダンス(系統インピーダンス)のリアクタンス成分(以下 Lz )の電流共振により系統連系制御が不安定に陥るという課題がある。この電流共振はACLインダクタンス値に対して Lz が大きくなればなるほど、共振周波数が低く、共振ゲインが大きくなる。 Lz が十分小さいと共振周波数が制御周波数より十分高くなるため課題とならない。一方、 Lz が大きいと位相が180 deg以上回っている周波数帯域で共振によりゲインが増加するため、ゲインマージン不足となり安定性悪化を引き起こす。従来はこれを懸念して想定される Lz 値に対して十分大きなACLインダクタンス値を設定していたため、ACLの小型化が制限されていた。
1.3 先行研究と本論文の位置づけ
ACLを小型化させるための方法として、制御ソフトウェアで共振を抑制させる方法が考えられる。
先行研究のうち系統インピーダンスを推定せず安定性を確保する手法として、文献 2)-4)は H∞ 制御や、LQG(Linear-Quadratic-Gaussian)コントローラといったロバスト制御を用いる例が報告されている。しかし、CPUの演算負荷がかなり大きいためPCSにとっては実用的ではない。
推定した系統インピーダンスを基に制御器を設計する手法も提案されている。文献 5)は高調波を出力電圧に注入し、振幅変動をもとにインピーダンス絶対値の推定を試みる。しかし、この手法では精度向上のために演算負荷が高いSOGI(Second Order Generalized Integrators) を複数実装する必要がある。文献 6)では有効・無効電力を変動させた際の出力電圧変動よりインピーダンスを推定する手法が提案されている。しかし、有効・無効電力を独立して操作するための制御系構築が必要であり、演算負荷が増加するという懸念がある。
本論文では、系統インピーダンスの影響を打ち消し、小さなACLでも安定となる手法を示す。補償器は先行研究よりも簡素な演算で実現した推定法による系統のインピーダンス推定値を元に、最適な補償器パラメータに調整するため、設置場所によって異なる系統インピーダンスに対して想定される Lz 最大値で設計する必要がない。そのため、さらなるACLの小型化を実現できる。
第2章では従来の制御系構築を行った際の系統インピーダンスの影響と課題を示す。第3章では系統インピーダンスの推定方法と補償器設計方法を示す。第4章ではシミュレーションの結果によって提案手法の有効性を示す。第5章にて本論文のまとめを述べる。
2. 系統連系制御への系統インピーダンスの影響
2.1 系統連系制御の構成
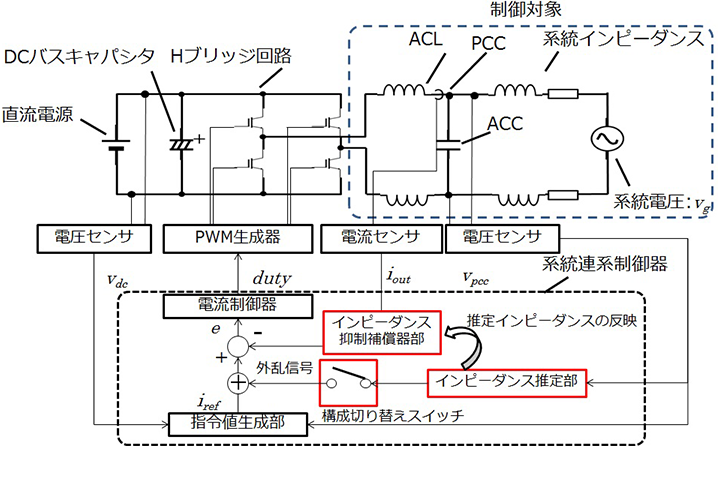
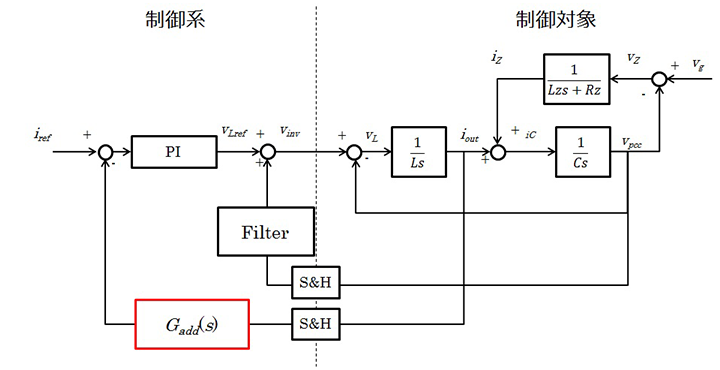
インバータの系統連系制御の全体像を図3に示す。系統連系制御は、系統連系点(PCC: Point of Common Coupling)の交流電圧位相と同期した電流指令値を生成する指令値生成部と、出力電流を制御する電流制御器と、インバータ回路、系統インピーダンス、系統電圧からなる制御対象で構成されている。制御系はPWM信号duty幅によりインバータ変調率を操作し、出力電流を制御する。
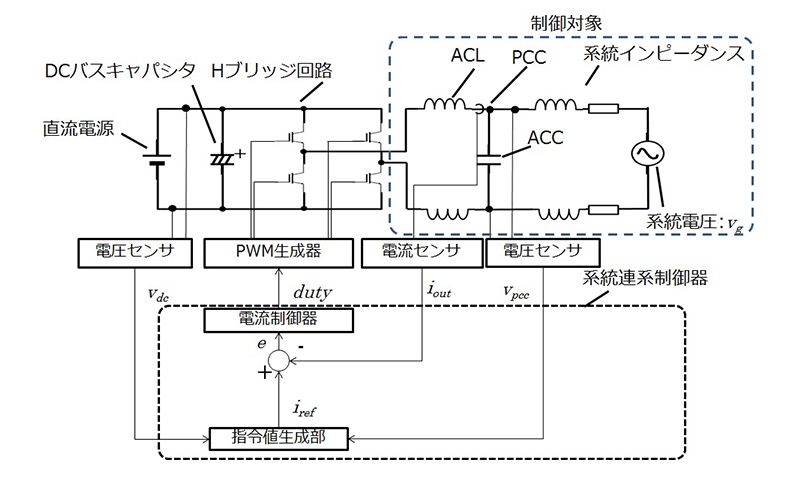
2.2 系統インピーダンスが引き起こす電流制御不安定
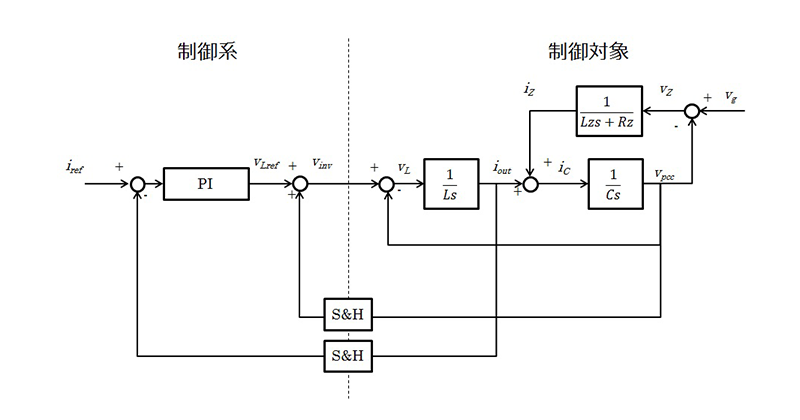
電流制御系の安定判別をMATLAB/Simulink上で実施するために、制御系と制御対象をモデル化した。図4にモデル化された電流制御系ブロック線図を示す。図5に電流制御系一巡伝達関数ボード線図を示す。各条件のパラメータは表1の通りである。
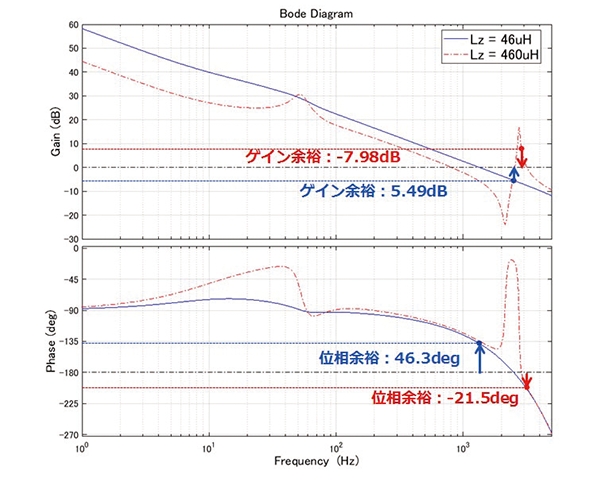
図5に実線で示されているグラフはLz =46 µH、Rz =38 mΩにおける一巡伝達関数を示す。制御系の安定度はゲイン余裕と位相余裕をもって評価される。ゲイン余裕は位相が180 deg回った地点での位相値である。Lzが十分に小さいので共振ピークは制御帯域(PWMキャリア周波数の半分)より高い周波数に発生するため、安定性を損なうことはない。この例ではゲイン余裕5.49 dB、位相余裕42 degとなっており安定である。また帯域幅は1 kHzを超えており、商用周波数より十分高く応答性も十分であると考える。
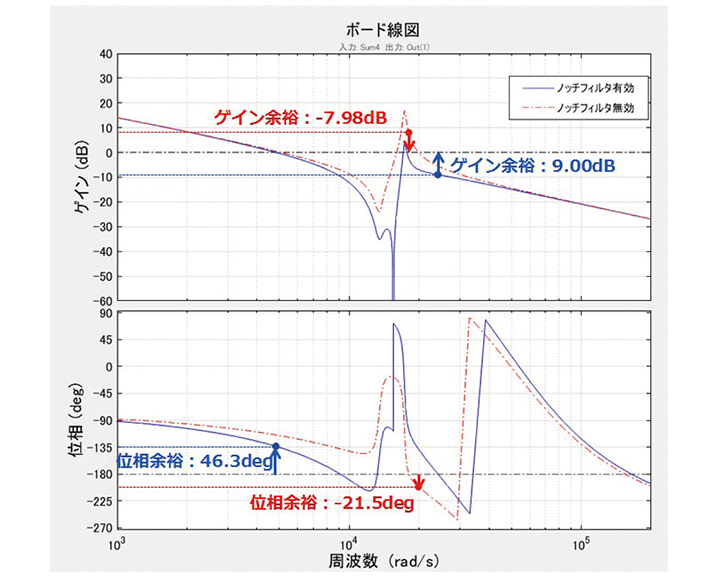
図5に破線で示されているグラフはLz=460 µH Rz=380 mΩの条件での一巡伝達関数を示す。Lzが大きくなったことで共振点がキャリア周波数より低くなったため、3 kHz付近で反共振が観測される。位相が-180 deg以下の領域でゲイン増加が起こっており制御不安定となる。ゲイン余裕は-7.98 dB,位相余裕は-21.5 degであった。これをPI制御のみで改善を行うと、帯域幅を減らさなければならず、高周波応答性が悪化し、出力波形が歪み、高調波規制を満たすことができなくなる可能性がある。
| 条件No. | 1 | 2 |
|---|---|---|
| 系統電圧 | 202Vrms | 202Vrms |
| 系統電圧周波数 | 60Hz | 60Hz |
| 系統インピーダンス虚部:Lz | 46uH | 460uH |
| 系統インピーダンス実部:Rz | 38mΩ | 380mΩ |
| ACリアクトル | 720uH | 720uH |
| ACキャパシタ | 12uH | 12uH |
| PWMキャリア周波数 | 10kHz | 10kHz |
| PI制御器 Pゲイン | 6.48 | 6.48 |
| PI制御器 Iゲイン | 454.4 | 454.4 |
3. 制御補償器の設計
3.1 系統インピーダンス推定手法
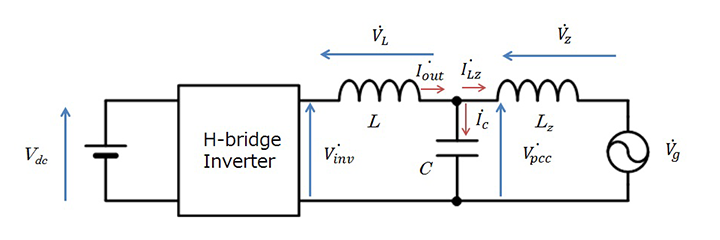
制御対象の等価回路を図6に示す。図6と後述する式ではACLのインダクタンス値を L、ACCのキャパシタンス値を C と表記する。系統インピーダンスにおいては Lz が支配的であると仮定し、Rz は省略する。
図6に示す系統連系点電圧は Vpcc 式(1)で表される。
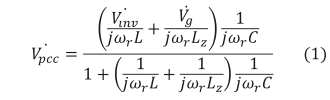
式(1)において、( V ̇pcc )が極大値となるのは、
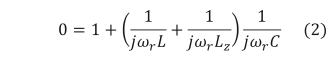
を満たすときであり、そのとき、 Lz は
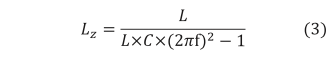
である(ただし、2πf=ωr )。図7に式(3)をグラフ化した結果を示す。
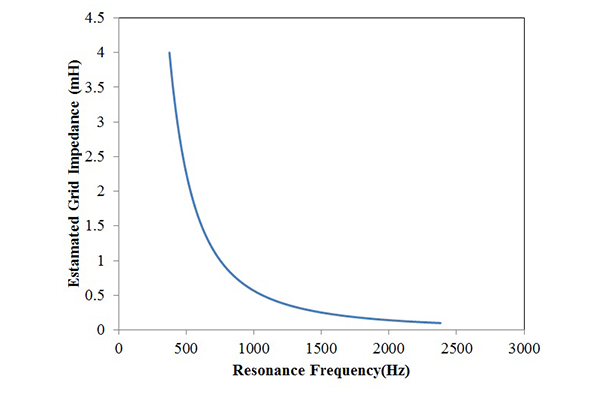
式(3)に示された変数のうちL, C は設計者が設定する値であるので既知である。そのため、何らかの方法で共振周波数 fcを推定し、式(3)の f に代入すれば、未知のパラメータ Lz を推定することが可能となる。電流制御系の指令値に小信号外乱を注入すると Vpcc に式(1)に示す形で応答が現れる。小信号外乱の周波数をスイープさせて Vpcc が最大となる条件を探索することで fc は推定可能である。
また、今回はインバータの出力フィルタがLCフィルタの例を示すが、LCLフィルタの場合でも同様に Lz を導出可能である。式(3)から得られる結果はLCLフィルタ系統側のACLインダクタンス値L2と Lz の和となるため、既知の L2 を引くことで同様に Lz を導出できる。
3.2 提案システムの構成とアルゴリズム
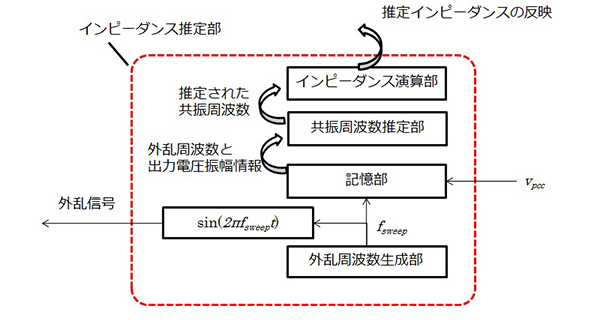
提案するシステム全体構成を図8に示す。これは図3に示した構成にインピーダンス推定部とインピーダンス抑制補償器部と構成切り替えスイッチを追加したものとなる。追加されたインピーダンス推定部の内部構成を図9に示す。
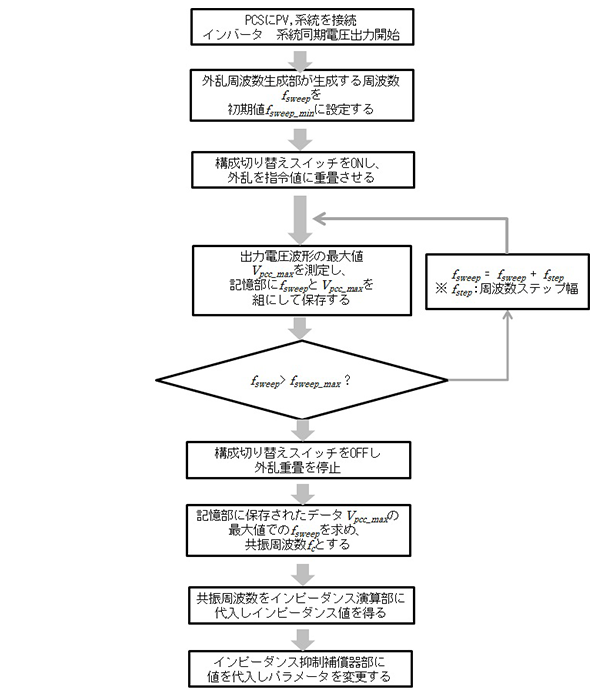
インピーダンス推定手順について述べる。PCSの制御系を動作させ、系統電圧と連系した電圧を出力する。この時、PCSが出力する電流は0で完全に系統と同期した電圧が出力される。次に、図9の外乱周波数生成部に重畳される外乱周波数 fsweep に初期値 fsweep_min を代入する。これにより、正弦波外乱生成部より外乱信号が生成され、構成切り替え部をONにすることで指令値に外乱信号が重畳し Vpcc に外乱電圧が重畳する。この時、外乱が重畳した Vpcc の最大電圧 Vpcc_max と現在出力している fsweep を組として記憶部に記憶し、外乱周波数に fstep を加えて更新する。これを外乱周波数が最大値 fsweep_max になるまで繰り返す。
最後に構成切り替え部をOFFにし、外乱重畳を停止させる。記憶した Vpcc_max のうち最大電圧をとった組をとりだし、その時の fsweep を共振周波数とする。この共振周波数 fc を式(3)の f に代入すれば系統インピーダンスを得ることができる。
スイープ範囲であるは設計者がL,Cの値を決定したのち、推定したい Lz の範囲を指定すれば式(3)を用いることで決定できる。
一連の動作をフローチャートにしたものを図10に示す。
3.3 補償器の設計
推定された系統インピーダンスから補償器を設計する。図6の等価回路モデルを元に電流の共振周波数 frcurrent を求めると式(4)のようになる。
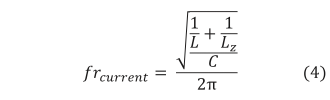
この式より得た frcurrent に不安定要素を引き起こす共振ゲイン増加が発生することがわかる。よって、その帯域のゲインを抑制する補償器 Gadd(s) を追加実装する。補償器の伝達関数を式(5)に示す。これは特定の周波数帯のゲインを低下させるノッチフィルタである。
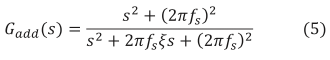
4. シミュレーション結果
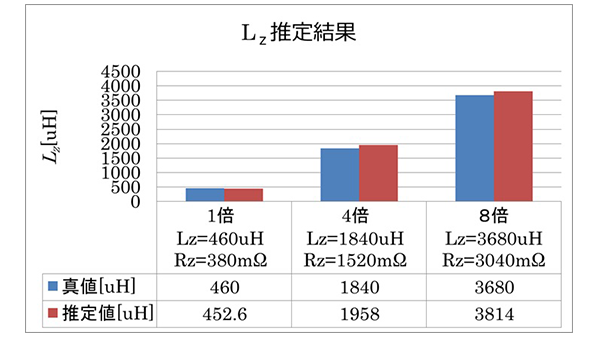
系統インピーダンスを推定するアルゴリズムをMATLAB/Simulink上で実装し、その精度を測定するためにSimscapeで実装した回路シミュレータと組み合わせてインピーダンス推定を行った。系統インピーダンス値 Lz およびRzは表1の条件2の値をベースに、1倍、4倍、8倍にした3条件で推定を行った。シミュレーションの結果を図11に示す。各条件で真値に近い推定値が得られている。
次に、推定されたインピーダンスを元に補償器の設計を行い制御不安定が改善するかどうかを確かめた。L および C は表1条件1のものを用いた。式(5)に Lz =460 µH Rz=380 mΩでの Lz 推定結果を代入すると、
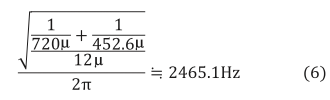
となる。
電流制御系安定判別を実施するために、図12に示すブロック線図をSimulinkで構築し、Gadd(s) ブロックに式(6)の結果を代入した。
図13に電流制御系の一巡伝達関数を示す。青の実線が補償器 Gadd(s) を追加した条件、赤の破線が補償器なし(図5 破線グラフと同一)条件である。補償器を追加することで安定な制御系を達成していることが把握できる。ゲイン余裕は9.0 dB、位相余裕は46.3 deg、帯域幅は769 Hzであった。図5の Lz =46 µH条件より帯域幅は狭くなっているものの、商用周波数において20 dB以上のゲインが確保されており、波形歪みへの影響は少ないと考える。
5. まとめ
本論文ではPCSインバータの出力フィルタLCおよびLCLタイプに対して、周波数スイープ法を用いて系統インピーダンスを推定する手法とインピーダンスを元に補償器を設計した例を示した。PCS設置後の系統インピーダンスに合わせて補償器を設計することで安定性を損なうことなくACLを小型化することができる。
この手法はインピーダンス推定部とインピーダンス抑制補償器部と構成切り替えスイッチ、そして2次系の補償器1つを従来構成に追加するだけで制御系の安定性を向上させることができるため、CPU演算負荷を大きく増やすことなくACL小型化に対するデメリットに対応することができる。
今後は、演算負荷が少ない設計でありながらインピーダンスの推定速度と精度を向上させることを検討していく予定である。
参考文献
- 1)
- International Energy Agency "Key World Energy Statistics 2017." https://www.iea.org/publications/freepublications/publication/KeyWorld2017.pdf (accessed:2018/02/19)
- 2)
- J. Chen, F. Yang and Q. Han. Model-Free Predictive H∞ Control for Grid-Connected Solar Power Generation Systems. IEEE Transactions on Control Systems Technology. Sept. 2014, vol.22, Issue 5, pp.2039-2047.
- 3)
- V. P. Singh, S. R. Mohanty, N. Kishor and P. K. Ray, Robust H-infinity load frequency control in hybrid distributed generation system. International Journal of Electrical Power & Energy Systems, March 2013, vol. 46, pp.294-305.
- 4)
- F. Huerta, D. Pizarro and S. Cobreces, LQG Servo Controller for the Current Control of LCL Grid-Connected Voltage-Source Converters. IEEE Transactions on Industrial Electronics, December, 2011, vol.59, Issue 11, pp.4272-4284.
- 5)
- J. Moriano, V. Bermejo, E. Bueno, M.Rizo and A. Rodriguez. A Novel Approach to the Grid Inductance Estimation based on Second Order Generalized Integrators. ECCE Cincinnati, October, 2017, pp.1794-1801.
- 6)
- M. Ciobotaru, R. Teodorescu, P. Rodriguez, A. Timbus, and F. Blaabjerg, Online grid impedance estimation for single-phase grid-connected systems using PQ variations. Power Electronics Specialists Conference, Jun. 2007, pp.2306-2312.


















