リレー高容量化を実現する動的挙動 シミュレーション技術
- リレー高容量化
- 動的挙動シミュレーション技術
- 開閉性能設計
- 電磁界解析
- 環境エネルギーマネジメント機器
近年、環境問題の取組みの一環として、電気機器のエネルギー効率化が推進されている。それに伴い、電子部品であるリレーにも小型化と高容量開閉性能の両立が求められるようになった。リレーの開閉性能を向上させるためには、金属接点の開閉動作および開閉時に発生するアーク放電現象、接点消耗過程を制御し、開閉性能を設計する必要がある。
そこで今回、シミュレーション技術で動的な金属接点開閉動作を制御設計することで開閉性能を向上させる取組みを行った。リレーの電気接点を駆動する電磁石の吸引力を電磁界解析により算出し、吸引力とばね弾性力から金属接点の動的な開閉動作を定量化した。今回の解析技術と実測評価を組み合わせることで、3倍の接点開離速度を実現し、開閉寿命を向上することができた。
1. はじめに
近年のハイブリッドカーや太陽電池パネル等の環境エネルギーマネジメント機器ではバッテリを利用するため直流が採用されている。また、これらの機器ではエネルギー効率化を追求するために機器の高電圧化、大電流化が進んでいる。これら環境エネルギーマネジメント機器には電路の開閉のためにメカニカルリレーが搭載されている。これら用途でのメカニカルリレーについては高電圧、大電流の直流を確実に遮断することが求められている。
一般的にメカニカルリレーやスイッチのように電気接点(以下、接点という)を用いて直流電流を遮断するには、接点開離時に発生するアーク放電の発生継続時間を短くすることが重要である。なぜならば、アーク放電はジュール発熱により高温状態になるため 1) 2)、接点表面を消耗させたり、接点周囲の部品変形を生じさせたりすることがあり、リレーやスイッチが故障する恐れがあるためである。そのため接点での直流遮断時は接点の開離速度を大きくし、短時間で接点間隔を確保することで、アーク放電の継続時間を短くすることが必要とされている 3)。
リレーの基本形であるシングル・ステイブル形リレーは、電圧印加した電磁石吸引力で接点対を閉じて、電磁石から電圧を除去したときのばねの力(以下、ばね負荷という)で接点対を開く構造となっている。したがって、電磁石のストロークに対する電磁石の吸引力およびばね負荷のバランスがリレー設計の基礎である。図1に電磁石ストロークに対する吸引力とばね負荷の模式図を示す。図1の模式図は、磁気吸引力が全ストロークにわたってばね負荷カーブを超えるようなコイル電圧を印加すると電磁石が動作することを示している 3)。吸引力カーブはコイル巻き線や磁性材で構成される電磁石の構造や材料、バネ負荷カーブは接点の動作範囲やバネ定数がそれぞれ設計要素になる。これらの要素を組み合わせて動作設計を行い、開閉の機能を実現していた。この図1は電磁石とばねのつり合いを表したもので、静的な動作設計(以下、静的設計という)である。
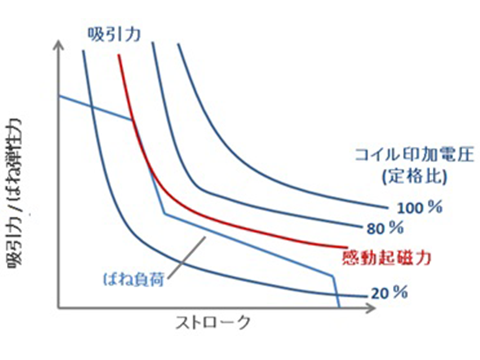
直流遮断に要求されるのは、素早い接点開離動作による短時間での接点間隔の確保である。すなわち、接点開離時の過渡的な挙動設計(以下、動的設計という)が必要である。しかしながら、動的設計は静的設計に比べ格段にパラメータが多いために理論的な手法確立が遅れていた。そのため従来の動的挙動設計は試作と実測検証を主体に行われていた。実測検証には試作評価が必要であり、開発リードタイムが長くなる問題がある。そこで今回CAEを活用して動的な接点開離動作の最適化を試みた。
2. テストサンプルと評価指標
2.1 テストサンプル概要
CAEの実施を行う上で接点開離動作の設計目標を明らかにするためにリレー原理モデルを作製して、その電気的耐久性試験を行った。図2にリレー原理モデル模式図を示す。今回の検討で用いた原理モデルは、ばね負荷の評価が簡便なコイルばねのみで構成されたリレー構造である。また、ヒンジ型電磁石の可動部に直接可動接点接続され、電磁石の可動部と可動接点とが完全に連動する構造とした。
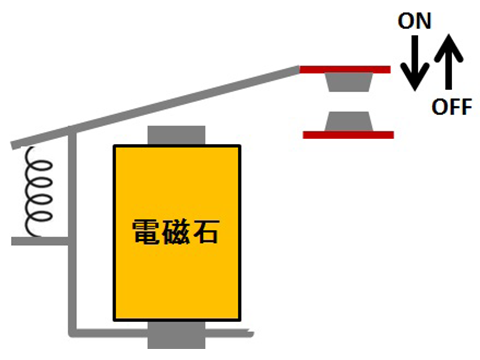
2.2 高容量化に伴う技術課題
図2で示したリレー原理モデルにて440 V/60 Aの負荷条件において電気的耐久性試験を行った。電磁石コイルにサージ吸収用ダイオードを接続して2,000回、サージ吸収用ダイオードを接続せずに50,000回の開閉寿命だった。図3にコイル駆動回路の回路図を示す。
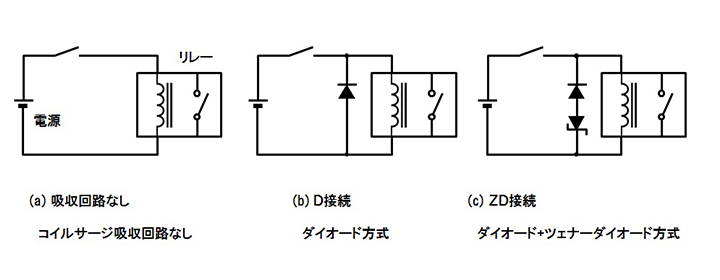
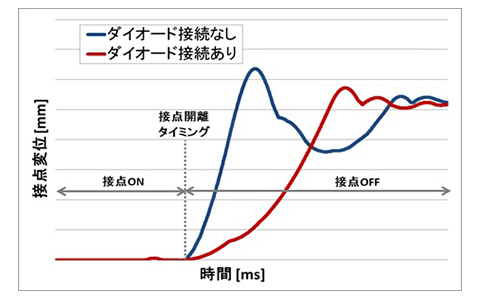
サージ吸収用ダイオードを電磁石コイルに並列に接続した図3の(b)の場合、スイッチオフ時に、コイル電流変化に伴う誘導起電力が発生する。これによりコイル-ダイオード間に誘導電流が流れ、吸引力が維持されることで接点開離速度が小さくなると考えた。そこで、ダイオード接続の有無による接点開離速度の差異と開閉性能の相関性に着目して、高速度カメラで測定した接点開離時の過渡的な接点動作をダイオード接続の有無で比較評価した。図4に接点開離時の過渡的な接点動作の実測評価結果を示す。図4の接点変位の傾きからも明らかなようにサージ吸収用ダイオードを接続した場合は接点開離時の接点速度が遅くなっていることが分かる。図4の接点が変位し始める接点開離タイミングから10 ms間の接点平均速度で比較すると、ダイオード接続した場合に比べ、ダイオード接続しない場合の方が約4倍大きい平均速度を持っていることが分かった。
これらのことから、過渡的なばね負荷と吸引力のバランスを定量化することで動的設計を行い、接点開離速度を最適化することが必要である。
2.3 溶着故障メカニズム仮説と評価指標
2.2で述べた接点開離速度と電気的耐久性試験の開閉寿命の相関性を評価するために、サージ吸収用ダイオードの有無やツェナーダイオードの接続などにより、意図的に接点開離速度を調整したサンプルを複数準備し、各サンプルで電気的耐久性の開閉回数と接点開離速度を評価した。図5に接点開離速度と電気的耐久性試験の開閉回数との相関性を示す。
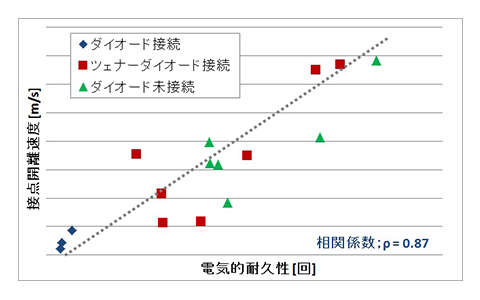
図5のグラフから接点開離速度と電気的耐久性試験の開閉回数は相関係数が0.87と非常に高い相関性を持っていることが分かる。図5で示した電気的耐久性試験の開閉寿命は、接点開離時に発生するアーク放電による接点消耗が起因となる接点溶着によるものである。接点溶着とは、接点同士がアーク放電により溶融し、接触した状態で再凝固する現象である。接点開離速度が遅くなり、接点間隔の確保に時間がかかると、アーク放電の継続時間が長くなり、接点消耗や接点溶融が発生しやすくなることが考えられる。このことから、接点開離速度を大きくすることで、接点溶着の故障頻度が低減できると考えられる。
これらのことから、アーク継続時間を短くし、接点消耗を抑えるための評価指標として接点開離速度を導入し、CAEにより接点開離速度の最適化を行う。
3. 解析内容
3.1 テストサンプル3次元CADモデル
図6にリレー原理モデルで用いた電磁石の3次元CADモデルを示す。
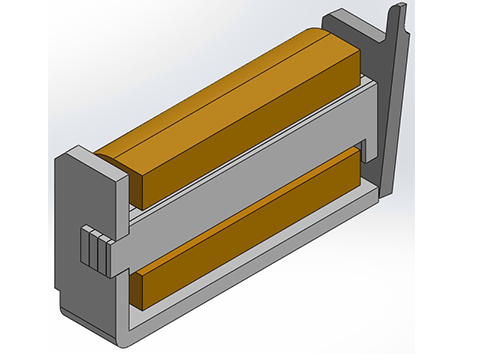
本モデルは図2のリレー原理モデルで用いた電磁石を3次元CADソフトSolid Worksで作成したものである。今回用いた電磁石モデルは対称構造のため、計算コスト低減を目的とし、対称面でカットしたハーフモデルとした。また、今回は電磁石と接点の挙動が連動した動きをするという前提に基づき、CAEにより算出した過渡的な電磁石挙動から接点開離速度を推定する手法を採用した。
3.2 電磁界解析による接点開離速度検討
3.2.1 解析モデル
図6で示した原理モデルの過渡的な挙動について電磁界解析をベースに計算を行った。図7に今回の電磁界解析モデルの計算フローを示す。今回の電磁界解析では、①電磁石駆動回路、②電磁石の吸引力、③電磁石可動部の過渡的挙動の連成解析を行い、電磁石挙動を算出している。
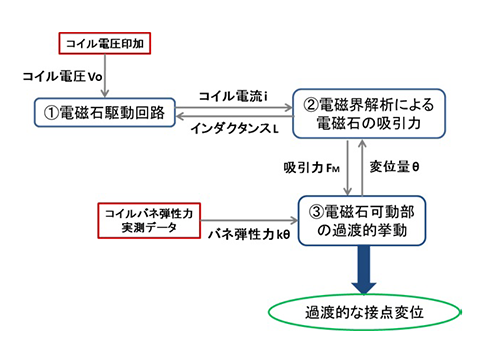
① 電磁石駆動回路
電磁石の磁界解析から算出されたインダクタンスLを基に(1)式により電磁石コイルに流れる電流iを算出する。
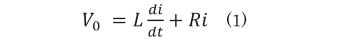
V0;コイル電圧、L;コイルインダクタンス
i;コイル電流、R;コイル抵抗
②電磁石の吸引力
(1)式で導出されたコイル電流iから、(2)式によりベクトルポテンシャルA、磁束密度B、電磁石可動部で発生する吸引力 FM を算出する。今回は過渡的に磁束密度変化が発生するため、過渡的な磁束密度変化を阻害する渦電流の発生を考慮した磁界解析を行っている 4)。
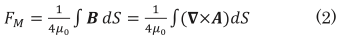
FM;電磁石の吸引力、µ0;真空の透磁率
B;磁束密度、A;ベクトルポテンシャル
③電磁石可動部の過渡的挙動
リレー原理モデルのヒンジ型電磁石可動部の挙動は回転運動と見なすことができるので、(2)式により計算された吸引力 FM を運動方程式(3)に挿入し各時刻の電磁石可動部の変位量θを算出する。(3)式で用いたバネ定数kについては、事前に荷重測定器により測定したバネ弾性力と変位量の関係から算出している。
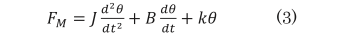
J;慣性モーメント、θ;電磁石鉄片の回転角
B;減衰定数、k;バネ定数
①~③の計算を各時刻で繰り返し行い、各時刻における電磁石可動部の変位を算出することで、接点の過渡的挙動の推定を行う。
3.2.2 解析結果
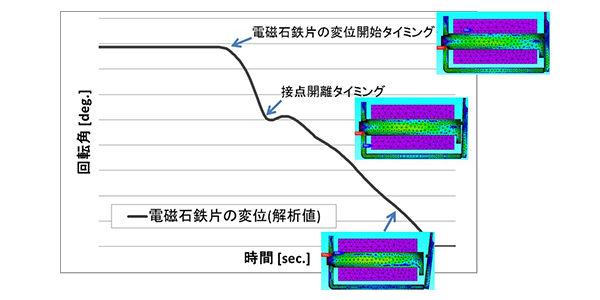
3.2.1で述べた解析モデルにて過渡的な電磁石可動部挙動を計算し、接点開離速度の推定を試みた。図8に電磁石挙動解析による電磁石可動部挙動のグラフ、および、代表的な変位での電磁石の磁束密度分布コンター図を示す。接点開離タイミングについては、電磁石可動部と金属接点が連動した挙動をするという前提で、解析的に算出した電磁石鉄片の変位開始位置と実際のリレー寸法から推定した。
3.2.3 評価方法
図8の電磁石可動部の過渡的挙動の解析結果から推定した接点開離タイミングを基準とし、その基準位置から10 ms間の平均速度を算出し接点開離速度とした。今回の検討では、電磁石の材質、形状の変更はせずに、ばね定数の大きさのみを変更することで、最も大きい接点開離速度が得られるばね負荷条件を解析的に検討した。接点の過渡的挙動は電磁石吸引力とばね弾性力の合力で決まるため、基本的にばね弾性力を大きくしていくことで、より大きな接点開離速度が得られると考え、より大きなばね定数を設定し、3.2.1で示した解析モデルを用い接点開離速度を算出する検討を行った。また接点開離速度とばね弾性力、電磁石吸引力との関係性の定量化を行った。
3.3 実機との比較
解析結果の精度評価を行うために、電磁石可動部の各変位における吸引力の大きさで実測値と解析値の比較を行った。図9に吸引力の実測値と解析値の比較結果を示す。実線が実験値、点列が解析値を表している。図8の点線枠で示した箇所が電磁石可動部と鉄心が完全吸着した位置を示しており、完全吸着位置のみ最大で5%程度の解析誤差だったが、可動部が動き出してからは1%を十分下回る解析誤差の精度を確保した。これは完全吸着時では吸着面の微小磁気ギャップに対して、磁性部材同士の接合部などのその他微小磁気ギャップ寸法の実機とモデルとの差異が無視できなくなるためと考えられる。今回の接点開離速度の検討では、吸引力解析誤差が1%以下の領域における電磁石可動部の解析データを用いるため、十分な解析精度が得られていると考える。
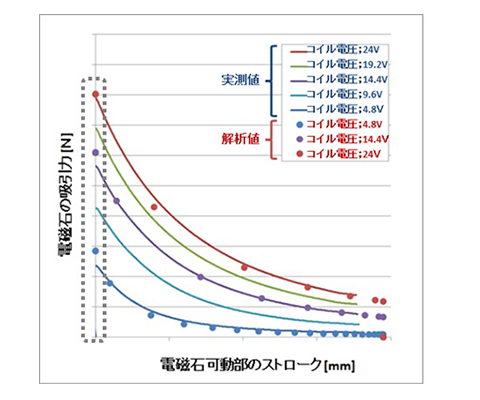
図10にコイル駆動回路に接続するサージ吸収素子、3種類のばね定数の各条件における接点開離速度の解析結果を示す。接点開離速度の解析値と実測値を棒グラフで示す。また接点開離時の吸引力、ばね弾性力を折れ線で示す。サージ吸収用ダイオード接続をした場合に比べ、ツェナーダイオードを接続した場合、ダイオードを接続しない場合の方が接点開離時の吸引力が小さくなっていることが分かる。
ダイオードを接続した場合、図3の(b)で示したように、リレー制御用スイッチOFF時にコイルとダイオード間でショート回路が構成される。この時、ショート回路内で(4)式に示したコイルの誘導起電力Vが発生し、コイルに一定時間誘導電流が印加される。これにより、吸引力が減少しにくくなり、接点開離時の吸引力が大きくなる。

(V;誘導起電力、L;インダクタンス)
吸引力が大きくなると、(5)式で表される接点開離力が小さくなり、接点開離速度の減少に繋がる。
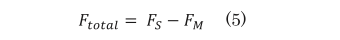
(Ftotal;接点開離力、FS;バネ弾性力、 FM ;吸引力)
これらのことから、ダイオードを接続しない場合は、接点開離速度を大きくすることができる。しかし、サージノイズによる電子機器保護の観点でダイオードは必要であるため、ダイオード接続条件において、接点開離速度の向上を検討する。
(5)式からばね弾性力を大きくすることで、接点開離力、および、接点開離速度の向上が期待できる。一般的にばね定数を大きくすることで、ばね弾性力を大きくすることができるが、図10に示したように、ばね弾性力が大きくなると同時に吸引力も大きくなることが分かった。
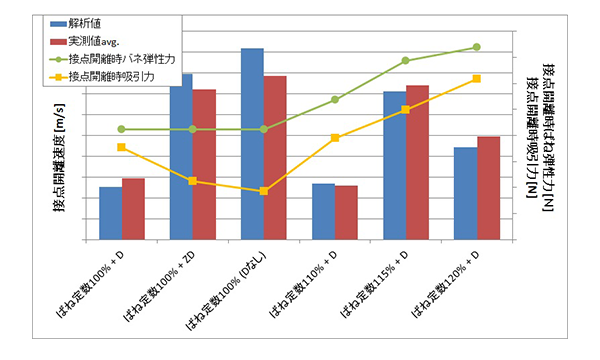
(棒グラフ;接点開離速度、折れ線グラフ;吸引力、ばね弾性力)
図11に接点開離時のコイル電流解析結果を示す。図中の矢印は電磁石可動部が動き出すタイミングを表している。ばね定数を大きくし、ばね弾性力を大きくすることで、電磁石可動部が動き出すタイミングが早くなる。これにより、電磁石可動部や接点が動き出すタイミングにおけるコイル電流が増大するため、接点開離時の吸引力も大きくなる。
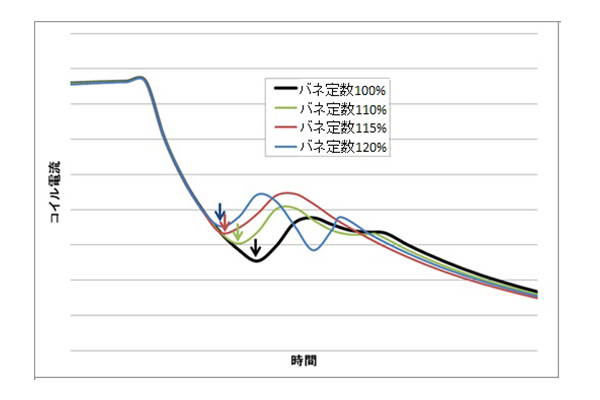
これらのことから、ばね定数を大きくすることで、バネ弾性力は大きくなるが、同時に電磁石吸引力も大きくなるため、図10で示したように接点開離速度は極大値を持つことが分かる。
4. 試作品への活用
図10の接点開離速度の解析結果を参考に最も大きな接点開離速度が得られるようにバネ定数を決定し、電気的耐久性試験の開閉寿命向上を目的とした試作品を作製した。表1にリレー原理モデルと今回の接点開離速度改善品の開閉性能比較を示す。今回の試作品では、基準となる原理モデルに比べ、接点開離速度が3倍となり、440 V/60 Aの負荷条件においては電気的耐久性試験の開閉寿命回数が約25倍となった。
| 負荷条件 | 開離速度 代表値 [m/s] |
電気的耐久性 代表値 [回] |
|
|---|---|---|---|
| 原理モデル | ダイオード接続 | 0.15 | 2,000 |
| 原理モデル | ダイオード未接続 | 0.48 | 50,000 |
| 試作品 | ダイオード接続 | 0.45 | 50,000 |
今回の検討においては、接点の過渡的な挙動を制御するために、ばね弾性力の増大を目的とし、ばね定数の最適化のみを行った。しかし、電磁石の磁気特性の最適化により、接点開離時の吸引力減少を実現できるため、電磁石の磁気特性も接点の過渡的な挙動を制御する因子になり得る。今回の電磁界解析と動的挙動解析を組合せた検討方法を用いると、電磁石の磁気特性の最適化も行うことができる。
5. まとめ
直流リレーでは接点消耗、接点溶着を低減するために、アーク放電の継続時間を低減する必要がある。アーク放電継続時間の低減のため、接点開離速度を大きくし、短時間で接点間隔を確保することが重要である。
今回、接点開離速度向上のため、電磁界と運動の連成解析により、接点開離時の過渡的な挙動を定量化する試みを行った。リレー原理モデルのばね定数を大きくさせると、バネ弾性力および電磁石吸引力が共に大きくなることが分かり、接点開離速度は極大値を持つことが分かった。
接点開離速度が最大となるバネ定数に変更した試作品にて、電気的耐久性試験評価を行うと、基準となる原理モデルに対し、開閉寿命回数が約25倍となった。これは、接点開離速度向上による接点消耗、接点溶融が抑えられたことが要因だと考えられる。
今後の課題としては、より複雑な実際のリレー構造について、本検討で行ったCAEによる接点の過渡的挙動の定量化手法を適用することである。本検討で用いたリレー原理モデルでは、電磁石可動部と接点が連動しているが、実際のリレーでは、電磁石可動部と接点が完全に連動することはない。これは、実際のリレーでは接点開離動作時に生じる接点可動部のたわみにより電磁石と接点の過渡的挙動に差異が発生することに起因する。今回の解析モデルでは、モデル全体を剛体として運動を取り扱ったが、実際のリレーの過渡的挙動を再現するには、接点可動部のたわみを考慮した計算モデルの構築が必要となる。たわみを考慮したリレー全体の挙動解析技術を構築し、実際のリレーの開閉寿命向上に貢献する技術開発を行う所存である。
参考文献
- 1)
- 電気学会放電ハンドブック出版委員会. 放電ハンドブック. 電気学会, 2003, p.1945
- 2)
- Fei Yang et al., Low-voltage circuit breaker arcs - simulation and measurements, J. Phys. D:Appl. Phys., 2013, Vol.46
- 3)
- 眞野 國夫. リレーハンドブック. 森北出版株式会社, 1992, p.335
- 4)
- 河瀬順洋, 菊池春秀, 伊藤昭吉. 直流電磁石の過渡動作特性の三次元数値解析. 電気学会論文誌B, 1991, Vol.111, No.10, pp.1051-1056.
















