Forecasting call arrivals at call center using dynamic linear model
- AI
- Time Series Analysis
- Space State Model
- Prediction
- Call Center
Many companies have call centers to answer telephone calls from their customers. Call centersŌĆÖ two major indices, service quality and running costs, have a trade-off relation; improving service quality needs additional operators, who require additional costs. To optimize the number of operators under the restriction of this trade-off, forecasting future call arrival volumes plays important role and accurate forecasting model is needed. Such model has to be capable of handling gradual fluctuations and effects of the special days (holidays, special events, etc.), and can be improved by utilizing knowledge of staffs. Dynamic Linear Model is a model with such capability. In addition, we can forecast the probability density of the call arrival volumes with this model, which can be utilized in determining the optimal number of operators.
In this paper, we propose a forecasting method using dynamic linear model, and also apply this model to a real data of a call center to show that we can make appropriate forecast of the future call arrival volumes over 2 months and thereby can reduce over-arrangement of operators by 39.3%.
1. Introduction
The OMRON Field Engineering Group (OFE) has a service network consisting of 140 operational sites and 1,200 customer service engineers spread across the country. Through this network, we serve customers all over the country with engineering, field, and backup services. Call center operations play one of the key functions in providing these services. The operations at call centers fall largely into two categories. The first one is outbound operations that involve operators making phone calls to consumers and others for telemarketing. The second one is inbound operations that respond to calls received typically through customer help desks. OFE╩╝s call centers mainly handle the latter of these two categories of operations. For inbound operations, the ratio of the volume of calls effectively answered within a predetermined time to the total volume of received calls is regarded as one of the important service quality indicators. Therefore, we have to keep a sufficient number of operators to answer received calls. At the same time, however, this gives rise to personnel costs. Accordingly, the number of operators must be optimized to strike the proper tradeoff balance between service quality and cost. At OFE, the sufficient number of operators to meet the required service quality level is calculated from the mean hourly call volume and the mean call duration in order to deploy personnel accordingly. The problem here is that the call volume and call duration at a future point are unknown. This means that the number of operators has to be calculated using values predicted from past data. Therefore, the forecast accuracy for call volumes or call durations is of critical importance.
In some simple forecasting methods, the mean values for the preceding month, those on a same month year-ago basis, and those for each of the seven days of the week are used unchanged. If, however, a call volume shows more complex fluctuations, such methods alone fail to make accurate forecasts. In such an operational situation, an analyst often has to rely on their experience and intuition to adjust forecast values with considerations given to fluctuation factors unique to their call center. This kind of operation poses challenges, such as a timeconsuming forecasting process and an analyst-dependent forecast accuracy.
These challenges have led to a proposal for various call volume forecasting methods. Among examples of these forecasting methods are those based on general time-series analysis models, such as ARIMA models or exponential smoothing models1’╝ē. These models can properly handle periodic fluctuations in time-series data. It is, however, difficult for them to handle patterns involving peculiar fluctuations unique to specific dates. Examples of forecasting methods for handling such peculiar fluctuations may include multiple regression model-based forecasts2’╝ē. A multiple regression model can easily take into explicit consideration fluctuation factors unique to individual call centers, in addition to calendar information such as years, days of the week, and week numbers, and therefore can serve as a model with high explanatory power. Multiple regression models, however, have difficulties in handling nonstationary time series that involve a gradual change in the mean value or in the magnitude of the impact from fluctuation factors. With data of this kind, they may show a gradual decrease in forecast accuracy over time. In actual call volume data, patterns have been observed with a change in the mean value or in the magnitude of fluctuations over time. Hence, we consider it necessary to develop a model capable of properly handling such changes.
Among the so-called state-space models, there are models called dynamic linear models. These models have more than one fluctuation factor and can flexibly handle time-series data containing unsteadiness, structural changes, or irregular patterns3’╝ē. Not only can these models easily take into consideration fluctuation factors unique to call centers, but can also make forecasts that follow long-term, gradual fluctuations. Moreover, what characterizes these models is their ability to determine the uncertainty of forecast results in the form of probability distributions. This allows quantitative evaluation of the occurrence probability of, and magnitude of, the error between forecast and actual results3’╝ē. We expect that, based on the probability distribution of the obtained error, we will be able take risk reduction measures of increasing the number of operators according to the magnitude of the predicted error on a day when a significant deviation from the forecast results is very likely to occur.
For this paper, we examined the results of dynamic linear model-based forecasts made for ATM-related call volume data handled at OFE╩╝s call centers for financial institutions. Our examination found that our model can make call volume forecasts up to two months ahead with reasonable accuracy and that the improved forecast accuracy helps to decide on more appropriate operator deployment.
This paper is structured as follows: Chapter 2 provides descriptions of call volume characteristics, Chapter 3 presents a dynamic linear model and describes specific models, and Chapter 4 presents the results of forecasts based on actual data.
2. Call volume characteristics
2.1ŃĆĆOverall tendency
Fig. 1 shows the plot of the volumes of intraday calls received at OFE╩╝s call centers from financial institutions in the period from April 1, 2015, to March 31, 2018. The first point revealed by the figure is that weekday call volumes significantly differ from those on Saturdays and holidays. Second, while the behaviors of the weekday call volumes exhibit a certain degree of seasonality, their fluctuation band is unstable and they as a whole constitute a non-stationary time series. Note that the solid line in Fig. 1 shows the moving mean of the weekday call volumes and can be regarded as a trend reflecting seasonal factors.
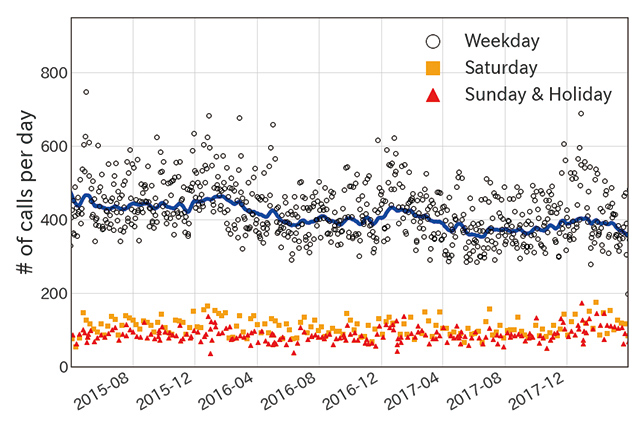
2.2ŃĆĆTendencies unique to call centers
Many of our call centers are considered to have their own tendencies that contribute to increases or decreases in call volume. We considered it possible to enhance the accuracy of forecasts by incorporating such tendencies identified through interviews with related frontline staff and observation of data.
<<<<<<< HEAD
OFE╩╝s call centers handle ATM equipment-related inquiries from financial institutions. It has been empirically known among frontline staff that the call volume tends to increase on days expected to see more frequent use of ATMs than usual. Such days include the 25th day of each month on which the monthly payday usually falls, the 15th day of each month on which the monthly pension payment day falls, and the days immediately before and after consecutive holidays. Data analysis has confirmed that such tendencies do actually exist (Figs. 2 and 3).
On the other hand, in some cases, data has revealed that some empirically assumed factors responsible for increases or decreases do not, in fact, make much difference. Therefore, it takes careful study to determine what factors are actually responsible for increases or decreases. For example, despite the traditional assumption that the call volume would increase on the first day of each month and the days in increments of 5 also known as the days ending in 5 or 0, no significant differences were detected from the available data (Fig. 4).
Hearing sessions were held with OFE personnel to make a list of factors probably responsible for fluctuations. We examined the magnitude of impact of these factors on call volume. Based on the obtained results, we decided to incorporate into the forecasting model the nine items shown in Table 1 as special factors responsible for fluctuations in call volume.
=======
OFE╩╝s call centers handle ATM equipment-related inquiries from financial institutions. It has been empirically known among frontline staff that the call volume tends to increase on days expected to see more frequent use of ATMs than usual. Such days include the 25th day of each month on which the monthly payday usually falls, the 15th day of each month on which the monthly pension payment day falls, and the days immediately before and after consecutive holidays. Data analysis has confirmed that such tendencies do actually exist (Figs. 2 and 3).
>>>>>>> dev
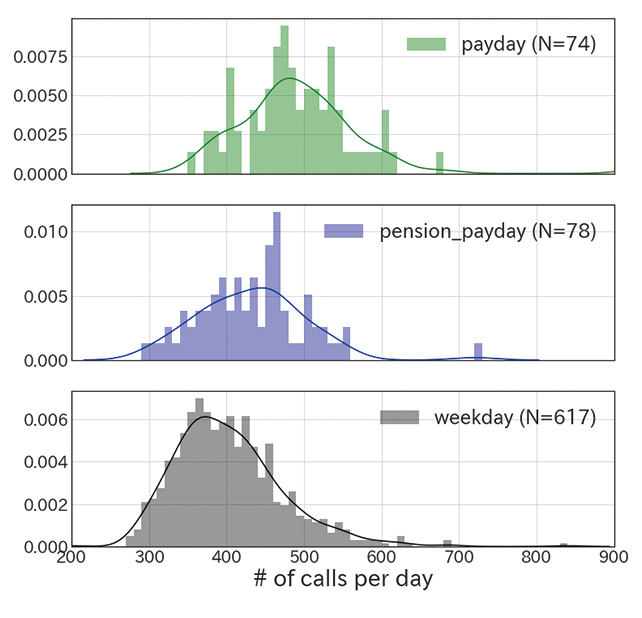
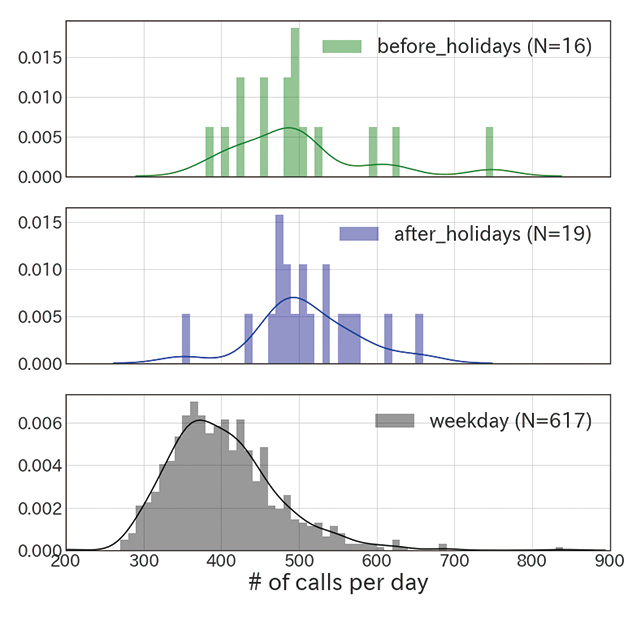
On the other hand, in some cases, data has revealed that some empirically assumed factors responsible for increases or decreases do not, in fact, make much difference. Therefore, it takes careful study to determine what factors are actually responsible for increases or decreases. For example, despite the traditional assumption that the call volume would increase on the first day of each month and the days in increments of 5 also known as the days ending in 5 or 0, no significant differences were detected from the available data (Fig. 4).
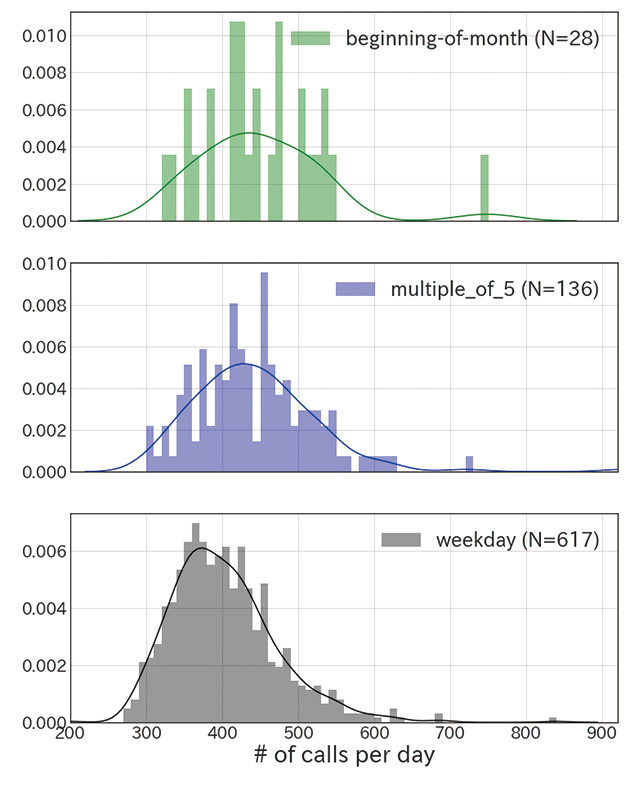
Hearing sessions were held with OFE personnel to make a list of factors probably responsible for fluctuations. We examined the magnitude of impact of these factors on call volume. Based on the obtained results, we decided to incorporate into the forecasting model the nine items shown in Table 1 as special factors responsible for fluctuations in call volume.
| Factor | Details |
|---|---|
| Saturday | Saturdays |
| Sunday or holiday | Sundays and national holidays |
| Year-opening business day | Year-opening business day |
| Year-end business days | The business days falling on and after December 20, and Fridays in December |
| End of each month | The last business day of each month |
| Payday | The 25th day of each month (if this day falls on a Saturday, Sunday, or a national holiday, the immediately preceding weekday) and the next business day |
| Pension payment day | The 15th day of each month (if this day falls on a Saturday, Sunday, or a national holiday, the immediately preceding weekday) and the next business day |
| Day immediately before consecutive holidays | The day immediately before three or more consecutive holidays |
| Day immediately after consecutive holidays | The day immediately after three or more consecutive holidays |
3. Methods of call volume forecasting
3.1ŃĆĆMultiple regression model
This section outlines a multiple regression model, which has been conventionally used to analyze time-series data including unique fluctuation factors such as those described in Chapter 22’╝ē. This multiple regression model is expressed by Equation (1). It is a model specified by regarding the subject as a linear combination consisting of an 




-
(1)
With the time-series factors of years, months, and days of the week included as explanatory variables, this model can be applied for time-series analysis. Moreover, it can be easily added with fluctuation factors other than time-series ones to provide an easy method of describing call center-specific factors responsible for fluctuations in call volume.
The multiple regression model, however, has difficulties in handling non-stationary time series with a moving mean over time. As can be seen in Fig. 1, the mean call volumes at OFE╩╝s call centers have been changing over the years. For such data, a model capable of more flexibly handling non-stationary time series is desirable.
3.2ŃĆĆState-space models and dynamic linear models3’╝ē
An example of model having characteristics such as those mentioned above is provided by a state-space model. Statespace models are highly flexible models applicable to time series containing unsteadiness, structural changes, or irregular patterns. Among these models, ones that is assumed to be linear and the noise of which is assumed to follow a Gaussian distribution are called dynamic linear models.
A state-space model does not directly model the fluctuations of the observed value 





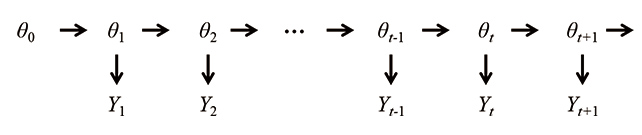
The formulation for our dynamic linear model is given as follows: the observed value 













-
(2)
<<<<<<< HEAD
where 






















=======
where 























>>>>>>> dev
Model learning occurs as a process that selects the parameters, means and variances of the Gaussian distributions that the above 

Let us assume here that there are random variables 












-
(3)
On the other hand, when the right-side term is the probability density of Gaussian distribution, its mean 


-
(4)
where 






-
(5)
3.3ŃĆĆFormulation for the dynamic linear model
Taking into consideration the call volume characteristics explained in Chapter 2, we created a call volume forecasting model based on the following idea:
First, let us assume that each expected intraday call volume is obtained by the expected base weekday call volume added or subtracted with the difference due to one of the fluctuation factors shown in Fig. 1. In addition, the expected weekday call volume and the magnitude of the difference due to the fluctuation factors are assumed to show random changes from day to day. Moreover, the actually observed call volume is assumed to be this expected value added with random deviations.
Let us assume then that each intraday call volume, the magnitude of increase or decrease due to fluctuation factors, and the magnitude of their intraday fluctuations respectively follow Gaussian distributions. Then, this model is formulated as below within the framework of dynamic linear models:
-
(6)
where the call volume to be predicted is 





It should be noted that the increase in the variance of the system error causes a proportional decrease in the forecast accuracy for the corresponding fluctuation factor, thereby suggesting the possibility that the actual value may significantly deviate from the forecast value. Hence, the forecast accuracy will be useful as, for example, an indicator for determining the adequacy of a selected fluctuation factor.
| dtype | Value | |
|---|---|---|
  |
Weekday | 6.6 |
| Saturday | 0.9 | |
| Sunday or holiday | 1.1 | |
| Year-opening business day | 16.0 | |
| Year-end business days | 0.0 | |
| End of each month | 12.1 | |
| Payday | 0.3 | |
| Pension payment day | 0.0 | |
| Day immediately before consecutive holidays | 910.5 | |
| Day immediately after consecutive holidays | 0.0 | |
| vt | ŌĆö | 1815.3 |
4. Test results
As explained in Chapter 2, our call centers receive ATM terminal-related inquiries from financial institutions. For the call volume data of this kind, we made forecasts using the model presented in Section 3.3. While the purpose of call volume forecasting is to optimize the work shift of operators, the work shift is usually determined at the latest several weeks before the beginning of the relevant month. Therefore, it is necessary to predict the call volume up to several weeks ahead when the work shift comes under consideration. In this paper, the results of call volume forecasts up to two months ahead are presented to suit the operations at OFE.
4.1ŃĆĆResults of two-month ahead forecasts
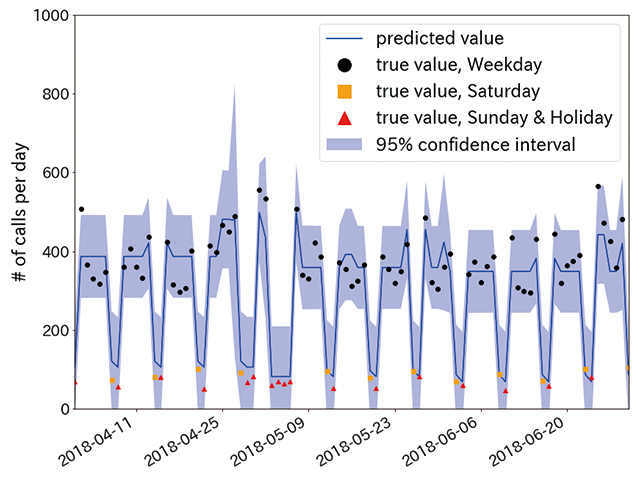
Fig. 6 compares the actual and predicted call volumes during the period from April 1, 2018, to June 30, 2018. Note here that a forecast was made for each month based on the data covering the period up to the last day of the second prior month to the relevant month (e.g.: the call volume forecast for the period from April 1 to 30, 2018, is based on the data for the period up to February 28, 2018). As shown in Table 3, 76 percent of the total call volume fell within a 68-percent confidence interval and 98 percent fell within a 95-percent confidence interval, thus indicating the validity of the forecast results.
In a dynamic linear model-based forecast, forecast values are given in the form of a probability distribution. Hence, a high risk of low forecast certainty due to large errors is made visible in the form of a higher variance of forecast values spread thinly in a wider confidence interval. As can be seen in Table 2, in the case of the model applied this time, the forecast values for increases and decreases due to a factor (day immediately before consecutive holidays) show a high variance, which means a lower forecast accuracy than on other days. The factors considered responsible for the lower forecast accuracy for the days immediately before consecutive holidays in the model used this time are first the sample size as small as 16 days for the days immediately before consecutive holidays, hence and second, the strong influence of outliers, and consequently and last, insufficient model learning.
| Outside 95% | 1 day (1.6%) |
|---|---|
| Within 95%, outside 68% | 14 days (22.6%) |
| Within 68% | 47 days (75.8%) |
4.2ŃĆĆComparison with multiple regression model-based forecasts
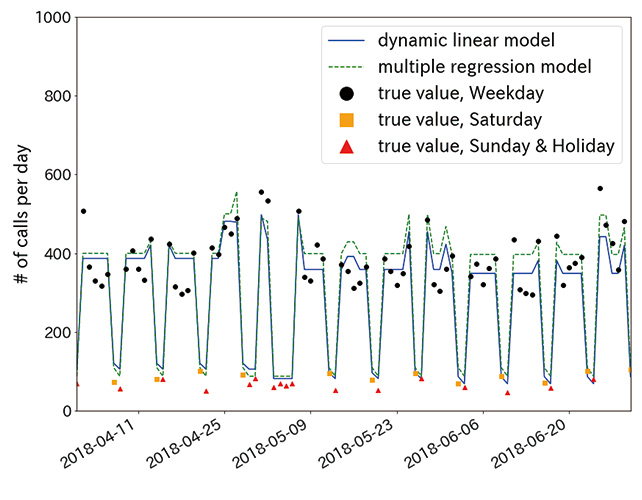
We also created a multiple regression model for use with the same fluctuation factors as those used in the dynamic linear model. This multiple regression model was intended as a baseline for comparison of the forecast results for the same data. While the dynamic linear model was designed for distribution estimation, the multiple regression model was designed for point estimation. Therefore, only predicted means were used for comparison. As in Fig. 7, the two models each showed forecast results generally similar to those of the other. Yet, a comparative evaluation of the forecast and actual results in terms of their mean squared errors revealed a 30-percent decrease from 3435.0 in the multiple regression model-based forecasts to 2389.9 in the dynamic linear model-based forecasts. Thus, even an evaluation only in terms of the point forecast accuracy confirmed that the dynamic linear model equals or outperforms the multiple regression model. It should be noted that on the whole, the multiple regression model predicted slightly larger call volumes than the dynamic linear model. This is due to the influence of the difference between the dynamic linear model that updates the mean 
4.3ŃĆĆOperator deployment optimization based on call volume forecasts
The purpose of call volume forecasting is to calculate the number of required operators and optimize operator deployment. Hence, we evaluated the effectiveness of call volume forecasts in terms of the magnitude of the difference between the number of required operators calculated from the predicted call volume and the optimal number of operators.
At OFE, the ratio of the volume of calls effectively answered within a specified number of seconds to the total volume of received calls is used as one of the service quality indicators. When calculating the number of required operators, the minimum number of operators is determined in such a manner that this indicator will exceed the predetermined level. Then, the number of operators thus determined is used. This indicator is calculated, using the Erlang C formula4’╝ē based on the number of operators 



For each of the weekdays in April, May, and June 2018 (62 days in total), the number of required operators calculated from the actual intraday call volume was regarded as the optimal number of operators and compared with the number of required operators calculated from the predicted call volume to determine the degree of overstaffing or understaffing. The results of this comparison are summarized in Table 4. Put simply, it can be said that the forecast accuracy increases with the increase in the number of days in the ┬▒0-person line highlighted in the table and with the decrease in the number of days in the other lines. For the parameters 

Using the conventional method in which the OFE staff relies on their experience and hunch to correct the past mean call volume, we predicted the call volume and compared the number of operators calculated using this predicted value with that calculated from the call volume predicted with the dynamic linear model. The comparison found that the number of days more overstaffed by one or more operators than the optimal number of operators decreased by 39 percent from 28 days to 17 days and that the number of days understaffed by one or more operators also decreased, albeit slightly, from 9 days to 8 days. Only excessive deployment of operators was reduced without compromising service quality. Hence, it can be said that a proper deployment of operators was achieved.
A comparison with the multiple regression model-based forecast results in terms of the number of operators reveals that the number of days overstaffed by one or more operators decreased by 29 percent from 24 days to 17 days whereas the number of days understaffed by one or more operators slightly increased from 8 days to 9 days. Although it is difficult to make a simple comparative judgment from this result, the staff deployment based on our method seems to be at least comparable with or better than that achievable by multiple regression model-based forecasting.
| Overstaffed/ understaffed by |
OFE calculation | Multiple regression model | Proposed method |
|---|---|---|---|
| ŌłÆ2 persons | 1 day | 1 day | 1 day |
| ŌłÆ1 person | 9 days | 7 days | 8 days |
| ┬▒0 persons | 24 days | 30 days | 36 days |
| +1 person | 26 days | 23 days | 17 days |
| +2 persons | 2 days | 1 day | 0 days |
5. Conclusion
This paper proposed a call volume forecast method based on a dynamic linear model. This dynamic linear model could flexibly handle the gradual fluctuations of call volume data with peculiar fluctuations encountered only under certain conditions.
For our test, we created a forecasting model for ATM-related call volume data handled at the call centers under the OMRON Field Engineering Group and examined the forecast results. The examination results revealed the following: our forecast results were valid with 76 percent of the actual call volume falling within a 68-percent confidence interval and 98 percent within a 95-percent confidence interval; a high forecast accuracy was achieved with the mean squared error lower by 30 percent than in the forecast made using the multiple regression model as the baseline; and an improved forecast accuracy effectively reduced excessive deployment of operators by 39 percent.
The call centers under the OMRON Field Engineering Group have spent approximately one day a month in manually performing call volume forecasting and developing operator deployment plans. The introduction of the forecasting method based on our dynamic linear model into this process allows a more appropriate deployment of operators and contributes to a significant reduction in workload. Currently, an experimental implementation is underway of a forecasting system based on our dynamic linear model, and its effectiveness has actually been confirmed.
<<<<<<< HEAD
Our method does not limit itself to call volume forecasting at call centers but allows its application to making various timeseries data forecasts. For example, non-stationary time series with a moving mean over time, which are difficult to handle with general time-series models, such as ARIMA models, or multiple regression models, our method particularly well serves the forecasting needs in such cases. There must be various data with similar characteristics. Among such data may be customer visit volumes and sales volumes at shops and stores and road and other traffic time series. We would like to apply our method to such data forecasts.
=======
Our method does not limit itself to call volume forecasting at call centers but allows its application to making various time-series data forecasts. For example, non-stationary time series with a moving mean over time, which are difficult to handle with general time-series models, such as ARIMA models, or multiple regression models, our method particularly well serves the forecasting needs in such cases. There must be various data with similar characteristics. Among such data may be customer visit volumes and sales volumes at shops and stores and road and other traffic time series. We would like to apply our method to such data forecasts.
>>>>>>> dev
Examples of the remaining challenges for our method are as follows: reviewing its structure or parameter update method to achieve higher forecast accuracy and devising a method of performing automatic identification and selection of fluctuation factors without assuming reliance on human knowledge5’╝ē.
References
- 1’╝ē
- Ibrahim, R.; Ye, H.; L╩╝Ecuyer, P.; Shen, H. Modeling and forecasting call center arrivals: A literature survey and a case study. International Journal of Forecasting. 2016, Vol.32, No.3, p.865-874.
- 2’╝ē
- Ito, M. Call Center Inbound Volume Forecasting. Unisys Technology Review. 2005, Vol.87, p.293-304 (in Japanese).
- 3’╝ē
- Petris, G.; Petrone, S.; Campagnoli, P. Dynamic Linear Models with R (translated into Japanese by Wago, H.; Hagiwara, J.). Tokyo: Asakura Publishing, 2013, 272p.
- 4’╝ē
- Chromy, E.; Misuth, T.; Kavacky, M. Erlang C Formula and its Use in the Call Centers. Advances in Electrical and Electronic Engineering. 2011, Vol.9, No.1, p.7-13.
- 5’╝ē
- Tahara, T.; Wang, Y.; Yamaura, Y.; Onishi, T. Towards Improvement of Call Arrival Prediction. Proceedings from the 31st Annual Conference of the Japanese Society for Artificial Intelligence. 2017, Vol.JSAI2017, p.1-4 (1L14) (in Japanese).
The names of products in the text may be trademarks of each company.
















