安定性解析とシミュレーションを活用した
サーボドライバパラメータ調整技術の開発
- 制御工学
- ゲイン調整
- サーボドライバ
- 周波数特性解析
- シミュレーション
近年の消費者ニーズの多様化に対応するために、変種変量生産を大量生産に劣らない低コストで実現する取り組みが盛んに行われている。その実現には、個々の装置でのタクトアップと装置立ち上げ時間の短縮が必要となる。特に、装置の重要パーツであるサーボドライバには、装置の最大性能を短時間で実現することが望まれる。しかし、現在主力となっている時間応答波形に基づくサーボパラメータ調整手法は、制御系の安定性を定量的に評価していない。このため、装置で実現可能な位置決め時間や追従誤差といった実現性能を十分に引き出せなかったり、装置の個体差やワーク変更といった僅かな動作環境の変化で、制御系が不安定になったりするという問題がある。
この問題に対して、装置を含む制御系の周波数解析を実施し、安定性を定量的に評価することで、調整の専門家ではなくても装置の最大性能を短時間に引き出せるサーボパラメータのオートチューニング手法を開発した。安定性解析には、実機だけでなくシミュレーションを活用し、装置の加振回数を削減することで、調整時間の削減と装置ダメージの抑制を図った。シミュレーションを活用することで、ノッチフィルタなどのサーボパラメータの組み合わせについて、一回の加振動作で約400通りの評価が可能になり、調整の専門家であっても調整時間の制約から到達が難しい実現性能を数分で達成可能にした。
本手法により、現場作業者には難解な調整完了条件設定が不要になるとともに、これまで数日かかっていた調整時間を数分に短縮した。その結果、顧客は装置本来のコンピタンス構築に集中することが可能になった。
1. まえがき
近年の消費者ニーズの多様化に対応するために、Just In Time生産方式に代表されるように、変種変量生産を大量生産に劣らない低コストで実現する取り組みが盛んに行われている。その実現には、個々の装置でのタクトアップと立ち上げ時間の短縮が必要となる。特に、装置の重要パーツであるサーボドライバには装置の最大性能を短時間で実現することが望まれる。これに応えるべくサーボドライバの搭載機能は多様化しているが、少子高齢化による労働人口の減少も相まって、サーボドライバの搭載機能を使いこなせる人材の確保・育成が難しい。これに対し、現在主力となっているサーボパラメータ調整手法は、装置を試運転したときの時間応答波形に基づくものであり、制御系の安定性を定量的に評価するものではない。そのため、装置で実現可能な位置決め時間や追従誤差といった実現性能を十分に引き出せなかったり、装置の個体差やワーク変更といった僅かな動作環境の変化で、制御系が不安定になったりするという問題がある1-4)。
そこで、装置を含む制御系の安定性を定量的に評価することで、調整の専門家でなくても装置の最大性能を引き出せるオートチューニング手法を開発したので紹介する。
2. 従来手法の課題
2.1 サーボドライバの役割と従来のパラメータオートチューニング手法
サーボドライバは、サーボモータの位置・速度をユーザからの指令値に追従させる制御機器であり、当社からは1Sサーボドライバシリーズ(図1)などが提供されている。サーボモータを使用するためには、サーボモータに電流を供給するサーボドライバに対してサーボパラメータの調整を行い、各種制御パラメータを装置に最適化する必要がある。特に、目標値と実測値の誤差補正感度であるフィードバックゲインや共振を除去するノッチフィルタ調整の良否が装置の実現性能や安定性に大きく影響する。

サーボパラメータの調整では、フィードバックゲインを大きくすると指令に追従できる周波数範囲(制御帯域)を拡げられるが、これを上げ過ぎるとゲイン余裕・位相余裕が不足し制御系が不安定化してしまう。従来の調整手法では、装置の時間応答波形を監視し、装置が振動を発生しない範囲でフィードバックゲインを最大化して指令追従性の向上を図っている。具体的には、装置にサーボパラメータ調整用の動作を行わせ、動作指令完了後から実際に装置が位置決め完了するまでの時間が目標以内になるまでフィードバックゲインを徐々に上昇させる。
2.2 従来手法の課題
2.2.1 制御構造の不適合
従来手法では、例えフィードバックゲインが適切に調整できていたとしても、サーボドライバの制御構造が顧客アプリケーションの目的に適合していない場合には十分な実現性能を得る事は難しい。
顧客アプリケーションの制御目的は、大きく2つに分類される。1つ目は、搬送アプリケーションの様に、目標位置までオーバーシュート無く最短時間で移動させる位置決め時間重視のアプリケーションである。そして2つ目は、レーザーカットアプリケーションの様に、目標軌道に偏差なく追従させることが重要な軌道追従性重視のアプリケーションである。
1つ目の位置決め時間を短縮するには、フィードバック制御系の制御帯域を拡大するとともに、目標軌道の加減速を抑制することも重要である。ユーザによって与えられた目標軌道の加減速が大きい場合には、装置の加減速に必要なトルクも比例して大きくなり、必要トルクがサーボドライバの出力可能範囲を超えた場合には制御不可能な状態に陥ってしまう。従って、位置決め時間を短縮するためには、フィードバック系に与える目標軌道がトルク飽和を起こしにくい制御構造を選択する必要がある。
2つ目の軌道追従性を高めるには、誤差が発生する前にフィードフォワード制御で補正することが重要である。従って、軌道追従性重視のアプリケーションでは、フィードフォワードトルクで装置をほぼ目標軌道通りに動かすことが可能な制御構造を選択する必要がある。
当社の1Sサーボドライバシリーズでは、これらの要求に応えるために複数の制御構造を搭載している。しかし、サーボドライバに搭載されている機能は多岐に渡っており、ユーザがこれらの機能を把握するには本来の業務とは関係の無い作業に多くの時間を割く必要があり、現実的には難しい。従って、サーボパラメータ調整はデフォルトの制御構造のままで実施されるケースが殆どであり、制御構造がアプリケーションの目的に適合していない場合には十分な実現性能を得られないという問題があった。
2.2.2 実現性能不足または安定性不足
従来の時間応答波形に基づくサーボパラメータ調整手法は、装置の安定性を定量的に指定及び評価することができないので、以下の何れかの問題が発生しやすい。
- 調整完了条件である目標整定時間が大きすぎると、フィードバックゲインを十分に上昇させることができず、装置で実現可能な性能を出し切れない。
- 調整完了条件である目標整定時間が小さすぎると、フィードバック制御系が不安定化直前のフィードバックゲインを選択される可能性がある。この場合、装置の個体差やワーク重量変化といった僅かな動作環境変動で実運転時に制御系が不安定化する。
2.2.3 動作範囲逸脱による装置破損
時間応答波形に基づくサーボパラメータ調整は、十分な加減速を伴う動作を行わせた上で動作波形を評価する必要がある。原理的に装置の移動量を大きくとる必要があるので、もしサーボパラメータの調整開始位置が装置の動作範囲限界近傍であった場合に、動作範囲限界を超えて装置を破損してしまうリスクがある。このことは、サーボパラメータ調整を行うオペレータの心理的負担になっている。
3. 本開発の内容
サーボパラメータ調整の専門家ではなくても、装置の限界性能を短時間で引き出せる調整手法として、Advanced Auto-Tuningを提案する。専門家以外では設定が難しい調整完了条件パラメータの設定を一切なくし、装置の制御目的を選択するだけの調整手法とした。本章の構成は以下の通りである。
3.1では、制御目的を指定するユーザインタフェースと選択される制御構造の特徴について説明する。
3.2では、装置の最大性能を引き出すための、安定性に基づくサーボパラメータの調整原理について説明する。
3.3では、サーボパラメータ調整時の装置動作範囲を数mm以内に抑制し装置破損リスクを低減する方法について述べる。
3.1 制御目的指定による制御構造の選択
3.1.1 調整ユーザインタフェース
本開発では、アプリケーションの制御目的に適合した制御構造が必ずしも選択されていないという問題の解決を目指した。そのため、制御目的を選択指定するだけで自動的に最適な制御構造が採用される方式とし、専門的な知見や装置の再起動などの煩雑なオペレーションを不要にした。
図2にAdvanced Auto-Tuningのユーザインタフェース画面を示す。画面の上段ではアプリケーションの制御目的を選択し、下段では調整強度を3段階の中から選択する。上段の制御目的で位置決め時間重視を選択した場合にはモデル追従制御構造が選択され、軌道追従性重視を選択した場合には100%フィードフォワード制御構造が選択される。下段の調整強度で、「High」を選択した場合には実現性能が優先され、「Low」を選択した場合には動作環境の変動に対する安定性が優先される。

選択される制御構造の特徴については、3.1.2以降に示す。調整強度の働きについては、3.2で述べる。
3.1.2 位置決め時間重視の制御構造
制御目的が位置決め時間の場合、サーボドライバはモデル追従制御構造を採用する。図3は、そのブロック線図である。モデル追従制御は、装置モデルを用いて制御シミュレーションを行うモデル制御ループ(同図上部)と実際に装置を制御するフィードバック制御ループ(同図下部)からなる。そして、モデル制御ループで得られた装置モデルの位置をフィードバック制御ループの指令値(内部指令値)として与える。
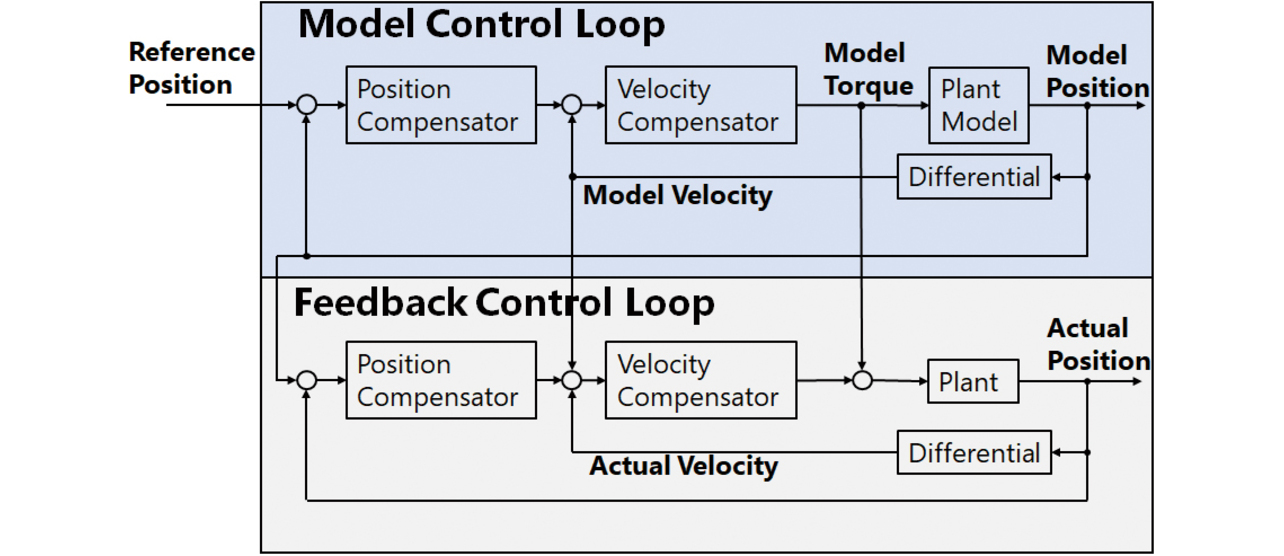
仮に、ユーザからの指令値が急激に変化してもモデル制御ループで実現できた装置位置をフィードバック系の内部指令値として与えるので、装置は内部指令値に対しては遅れなく追従できる。つまり、モデル制御ループが、目標軌道に含まれる周波数成分から制御対象が追従できない周波数成分を取り除くローパスフィルタとして作用している。このことは、ユーザ指定の指令値に対して乖離があるものの、整定時にオーバーシュートが発生しない目標軌道を内部的に生成していることに相当する。これにより、目標軌道をそのままフィードバック制御ループに与えてオーバーシュートが発生する場合より、整定時間を短くしている。
また、目標軌道は台形速度で指定される場合が多いが、モデル追従制御構造は最大速度を高く設定し易い。これは、位置軌道の2回微分である加速度は必要トルクに比例するが、モデル制御ループのローパスフィルタとしての作用が加減速に必要なピークトルクを抑制するからである。
3.1.3 軌道追従性重視の制御構造
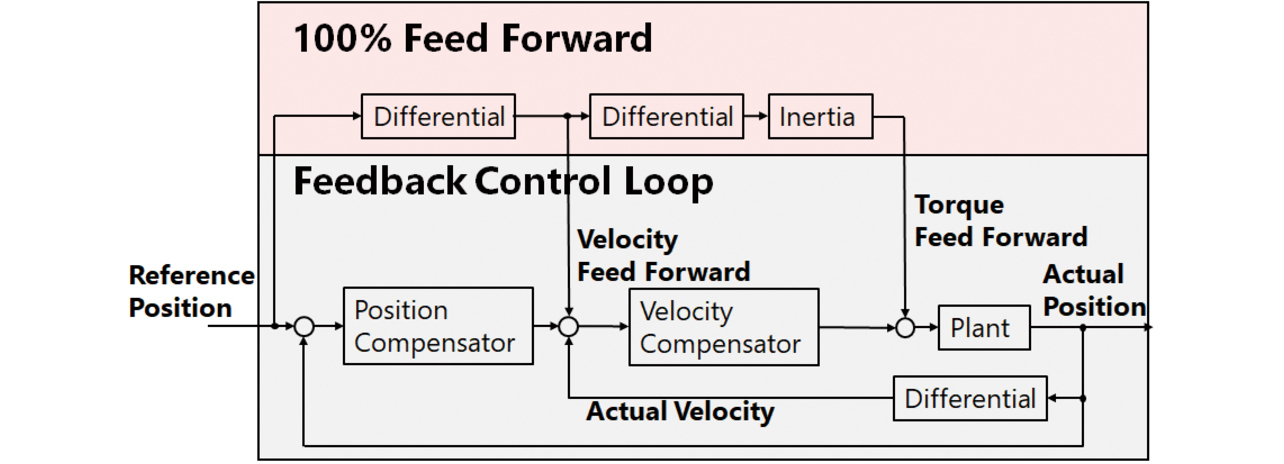
制御目的が軌道追従性重視の場合、サーボドライバは100%フィードフォワード制御構造を採用する。図4は、そのブロック線図である。同図上部がフィードフォワード部で、下部がフィードバック制御ループである。制御対象を単慣性で近似できる場合は、フィードフォワード部で目標軌道から計算した必要トルクを制御対象に与えるだけで、実際の装置もほぼ目標軌道に近い動作を実現できる。モデルと実機の相違から発生する僅かな誤差は、フィードバック制御ループで補償する。目標軌道に装置が追従できない高周波成分が含まれない場合には、フィードフォワード制御の効果で高い軌道追従性能を実現できる。
3.2 安定性に基づくサーボパラメータ調整
装置の最大性能を引き出すためには、装置で実現可能な性能限界を定量的に把握した上で調整を行う必要がある。Advanced Auto-Tuningは、周波数解析機能(FFT解析)を用いてフィードバックゲインを変数とする制御系の安定性マップを作成する。この安定性マップを用いてアプリの制御目的に沿ったサーボパラメータ調整を行う。その具体的な方法は、3.2.1に示す。
安定性解析に必要な実機データ取得回数は、時間削減及び装置ダメージの観点から最小限に抑えたい。そこで、ある1条件でのデータ取得後は、シミュレーションを用いることで実機データ取得回数の削減を図る。シミュレーションを用いた安定性マップの作成方法について3.2.2に示す。
また、制御帯域を拡大するためには、フィードバックゲインの他に、機械共振を抑制するノッチフィルタの数や減衰特性の最適化も重要である。実際、ノッチフィルタの最適化により、制御帯域を数倍拡げられるケースも存在する。フィードバックゲインとノッチフィルタ形状の最適化で安定性を向上させ、制御帯域を拡大する手順について3.2.3に示す。
以上に加え、安定性マップを使用したサーボパラメータの自動調整フロー全体を3.2.4に示す。
3.2.1 安定性マップによるフィードバックゲインの調整原理
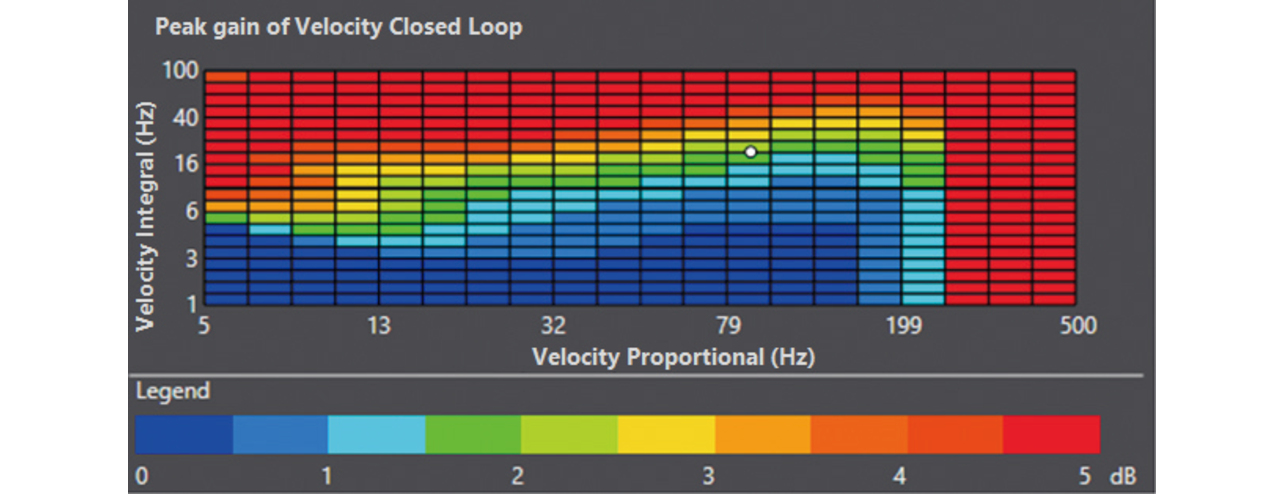
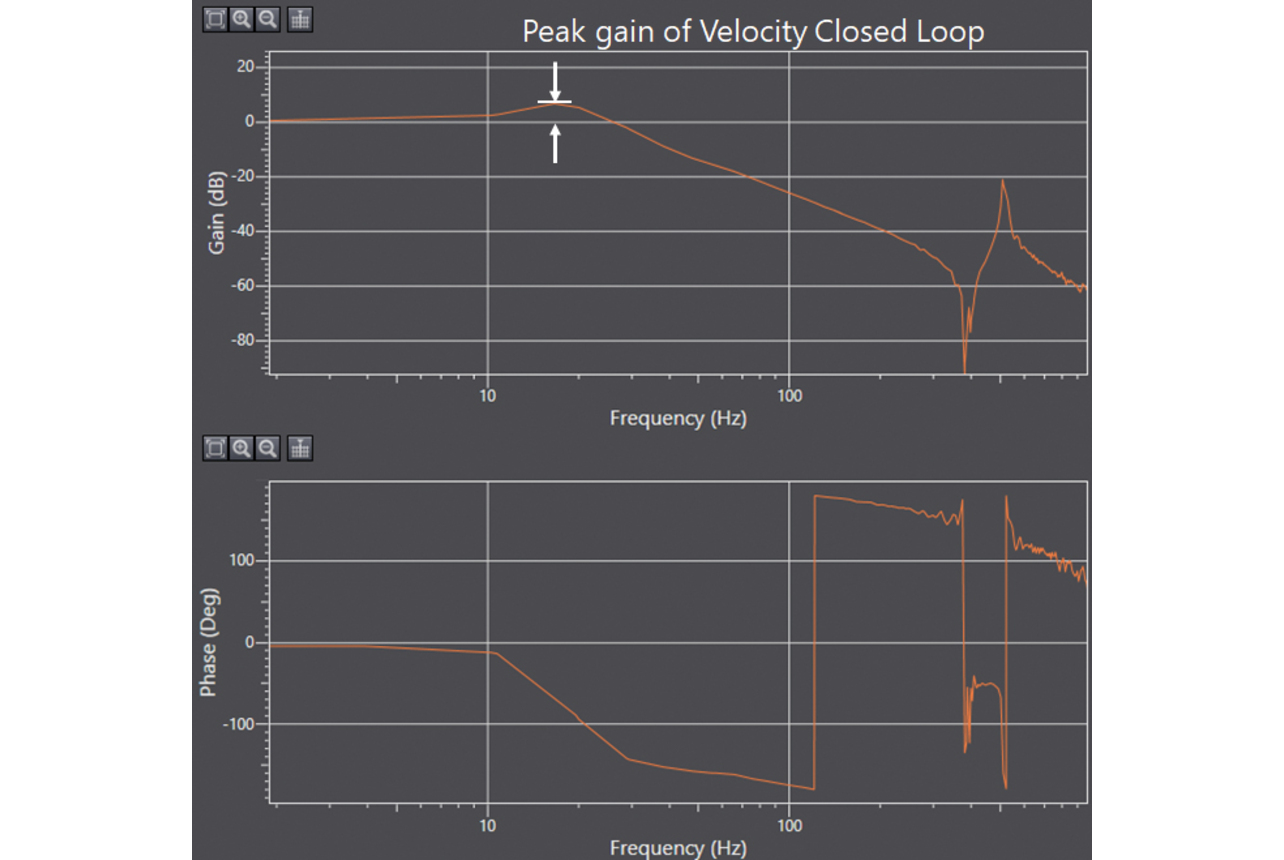
図5に速度制御ループの安定性マップを示す。これは、横軸を速度比例ゲイン、縦軸を速度積分ゲインとした時の安定性をコンター図として表現したものである。安定性は、マップ領域を微小区間に分割し、その区間の代表ゲインを用いて装置を加振試験した時のFFT解析結果より決定する。図6にFFT解析により求めた速度閉ループの周波数伝達関数をボード線図として示す。望ましい速度閉ループのゲイン特性は、出来るだけ高周波数まで0 dBであることである。ゲインが0 dBとは指令速度に対して装置の実速度も同じ大きさであることを示す。ゲインが0 dBより大きければ、指令速度に対して装置の実速度の方が大きく、制御系が不安定化し始めていることを示唆している。このボード線図のゲインピーク値を安定性と定義し、0 dB以下を青色の安定領域、5 dB以上を赤色の不安定領域として定義した。
次に、安定性マップを用いた実現性能と安定性のトレードオフの図り方について述べる。高周波指令への追従性能は、速度比例ゲインに比例する。従って、ユーザによる調整強度が「High」の場合、安定性マップの安定領域内においてできるだけ大きな速度比例ゲインを選択する。速度積分ゲインに関しては、速度比例ゲインと同様に安定領域内においてできるだけ大きなゲインを選択することが考えられる。しかし、装置の摩耗原因となるオーバーシュート抑制の観点から、係数図法5)に基づき速度比例ゲインの1/4とした。
ユーザによる調整強度が「Middle」および「Low」の場合は、環境変動に対する安定性をより重視し、安定性指標が0 dB未満となるフィードバックゲインの組み合わせの中から選択する。このことは、安定性マップの安定領域のより内側のゲインセットを選択することに相当する。
位置制御ループゲインの決定については、速度ループのフィードバックゲイン決定後、位置比例ゲインをパラメータとした安定性マップを作成し、速度ループと同様に調整強度に従った安定性を確保できるゲインを選択する。
3.2.2 シミュレーションを活用した安定性マップの作成
安定性マップを作成するには、マップ領域の微小区間数だけFFT解析を行い、更に得られたボード線図からピークゲインを求める必要がある。これら全てに対して実機を用いて実施すると、データ収集時間及びFFT解析時間が膨大になる。また、加振回数の多さから装置へのダメージも危惧される。そこで、安定性マップの作成にシミュレーションを活用することで、安定性マップの作成時間削減と装置へのダメージ抑制を図る。
図7に、速度制御ループのブロック線図を示す。安定性の評価は、速度閉ループのゲインピークで行う。これについては、図7から明らかな様に一度装置の周波数伝達関数が判れば、その他の制御補償要素は既知であるので、実機を用いた加振試験を行う事無く速度閉ループ周波数伝達関数の計算が行える。
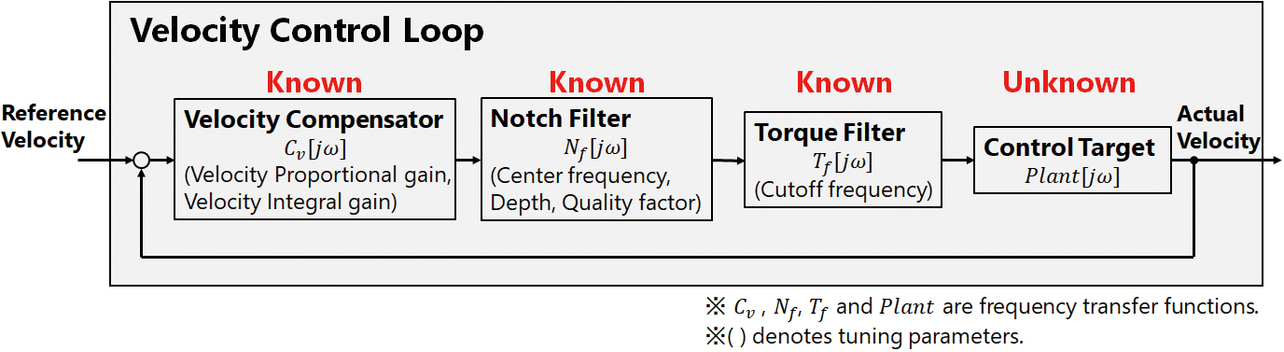
尚、装置の周波数伝達関数はトルク指令を入力とした開ループの加振試験で求めることが一般的だが、本提案手法では制御系が閉ループの状態で加振試験を実施している。これは、開ループ状態で加振試験を実施すると装置の移動距離が特定できず装置破壊につながるおそれがあるからである。また、フィードバック制御が実施されていないと装置が落下する垂直軸に対応するためでもある。
図8にシミュレーションを活用した安定性マップの作成フローを示す。
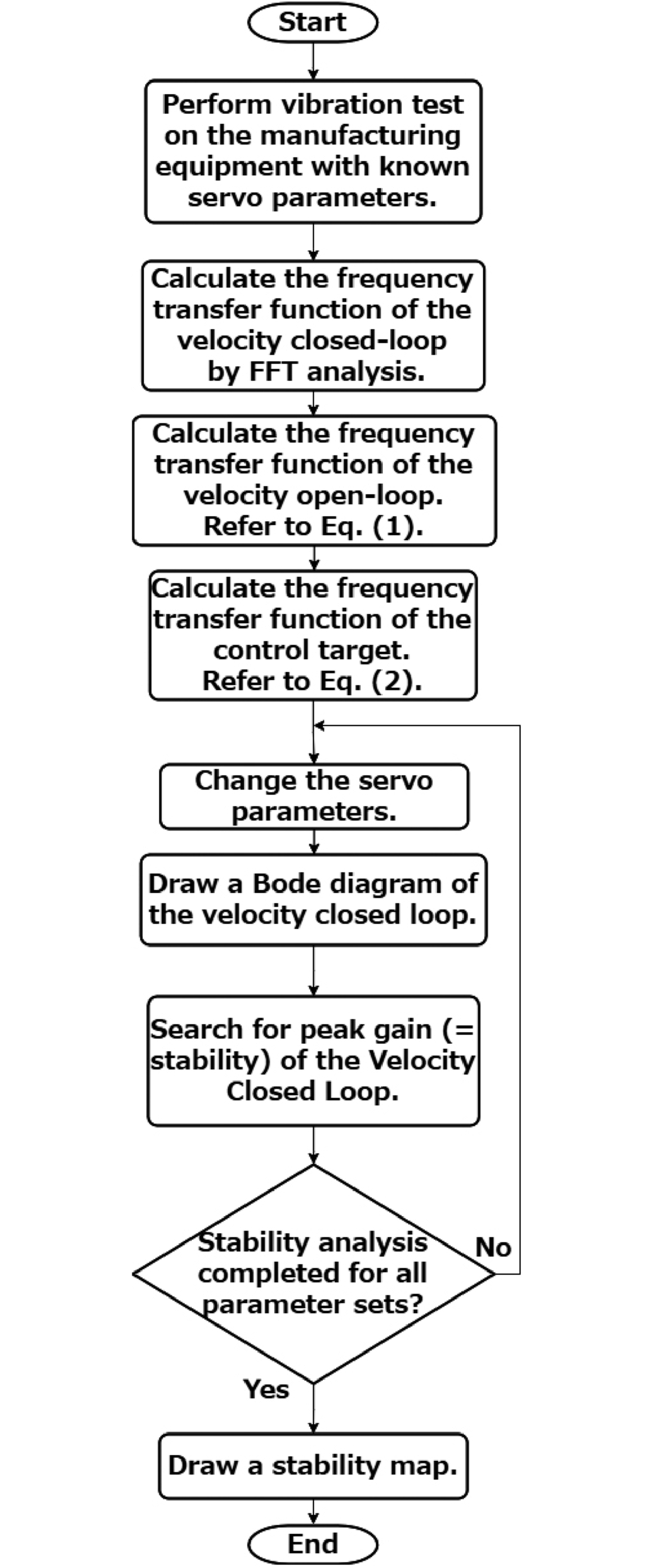
まず、既知のサーボパラメータを用いて図9に示す加振パタンで装置の加振実験を実施する。得られた入出力波形からFFT解析を実施し、図6に示す速度閉ループのボード線図を得る。図6の上段がゲイン線図、下段が位相線図になっている。次に、得られたゲインと位相を複素数表現することで周波数伝達関数(









一度 

3.2.3 安定領域の最大化
3.2.2ではフィードバックゲインを変更した場合の安定性マップの導出方法を述べたが、速度ループの補償器にはその他にノッチフィルタやトルクフィルタも存在する。これらのフィルタパラメータの調整の良否は、安定領域すなわち速度制御帯域の大きさに大きく影響する。これまではサーボパラメータ調整技術者が、ボード線図を視察しながらフィルタパラメータの最適化を実施していた。そのため、調整時間の制約から十分に最適化が行えるとは限らなかった。本提案手法では、フィルタパラメータにもシミュレーションを活用している。これによって、幅広いパラメータの組み合わせについて安定性を評価し、最も安定領域が広がるフィルタパラメータを選択している。
3.2.4 サーボパラメータ自動調整フロー
図10にサーボパラメータの自動調整フローを示す。自動調整の流れは、次のようになる。
- (a) 速度ループの周波数解析結果に基づきシミュレーションを活用して安定性マップを作成する。
- (b) ユーザが指定した調整強度に従って、速度ループのフィードバックゲインを仮決定する。
- (c) (b)で仮決定したフィードバックゲインを用いて再度実機を用いた加振試験を実施し、安定性マップの精度を改善する。
- (d) ノッチフィルタパラメータ(中心周波数、深さ、Q値)を変更する。当社独自のアルゴリズムに従って、安定領域が最大となるノッチフィルタパラメータを探索する。
- (e) ノッチフィルタパラメータの変更で安定領域が更に拡大していれば、(b)に戻って再度フィードバックゲインの向上を試みる。安定領域を拡大できなければ、ノッチフィルタパラメータを確定し、位置ループのフィードバックゲインの決定に進む。
- (f) 位置フィードバックゲインを変更した場合の位置ループの安定性マップを作成する。
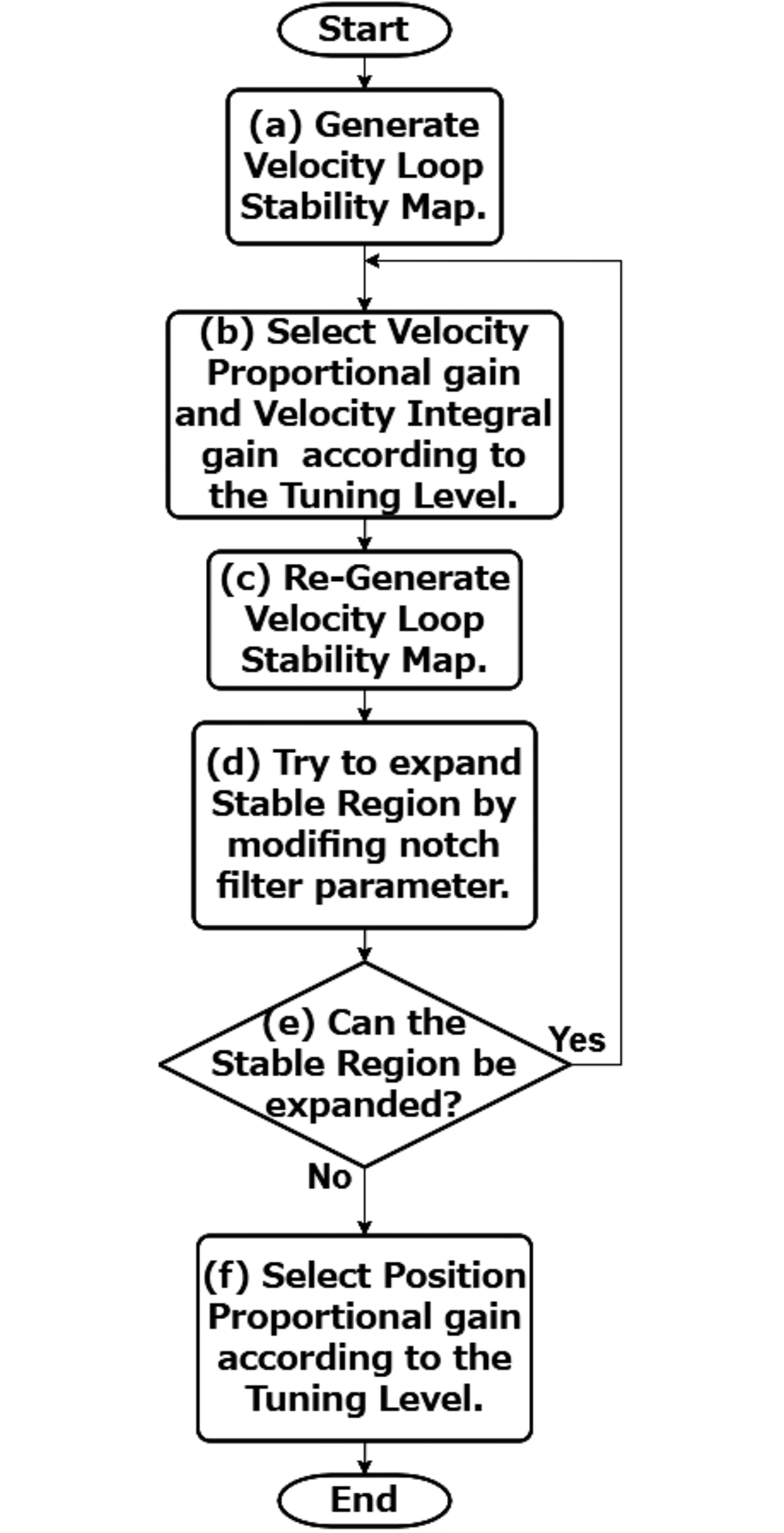
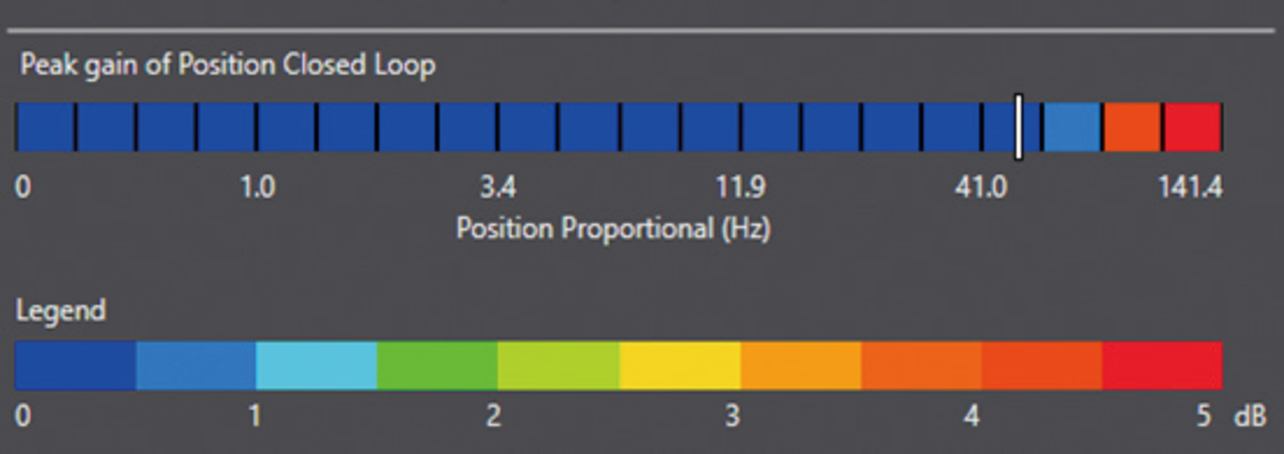
図11に位置ループの安定性マップを示す。位置ループの補償器は位置比例ゲインのみなので1次元のマップとなっている。速度ループと同様に、ユーザが指定した調整強度に従って実現性能と安定性のトレードオフを図り、適切な位置フィードバックゲインを決定することができる。
3.3 調整時動作範囲の抑制
本提案手法は、装置を加振しその周波数解析結果に基づきサーボパラメータを決定する。速度のフィードバック制御が有効な状態で装置を加振するので、移動量が確定的であり、周波数解析に必要な指令値の振幅が数mm以内である。このことから、装置が意図せず動作範囲外に移動し破損するリスクは小さい。
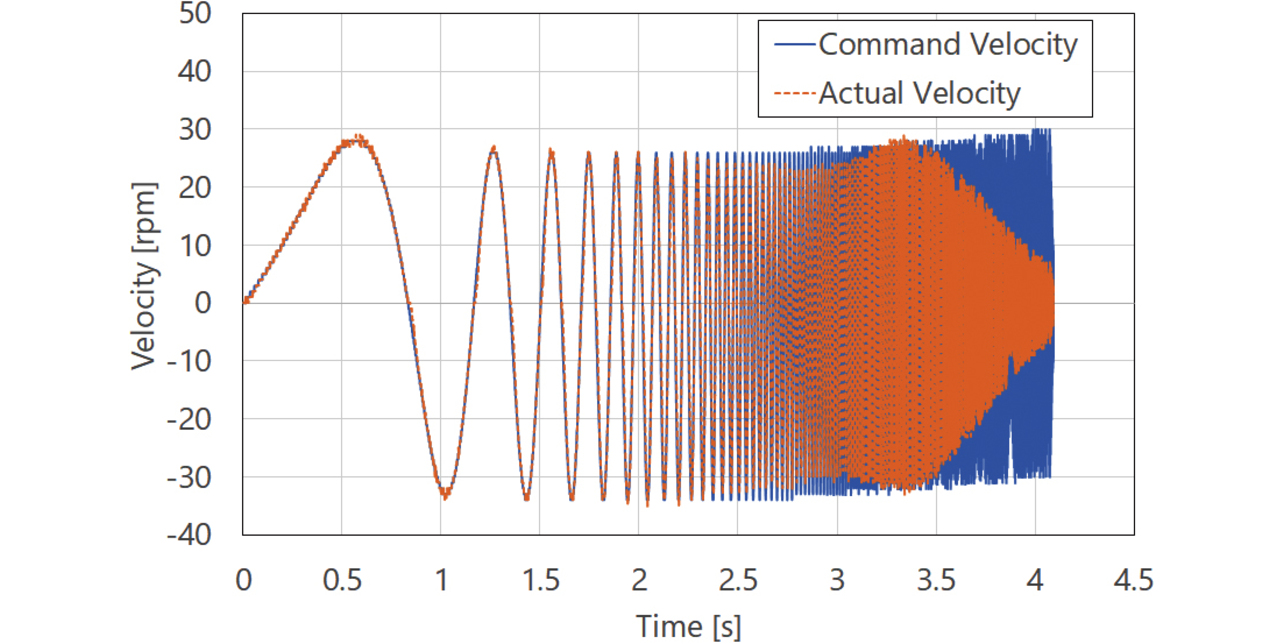
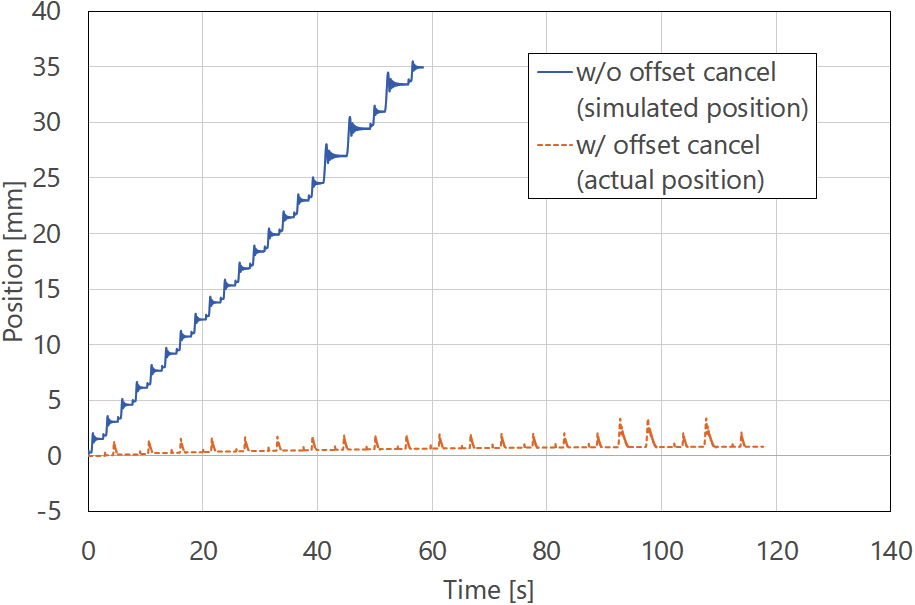
しかし、3.2.4のサーボパラメータ自動調整フローで示した通り、安定性マップの精度をより確からしくするために加振操作を繰り返し実施している。もし、加振操作の度に装置の現在位置が徐々に移動すると、最終的に装置が動作範囲外になるおそれがある。図12に実線(w/o offset cancel)で、一般的な周波数解析用の加振信号波形を示す。時間とともに加振周波数を掃引するSweptSine波形であるが、最終的な位置が加振開始位置から移動してしまう(図13の実線:w/o offset cancel)。
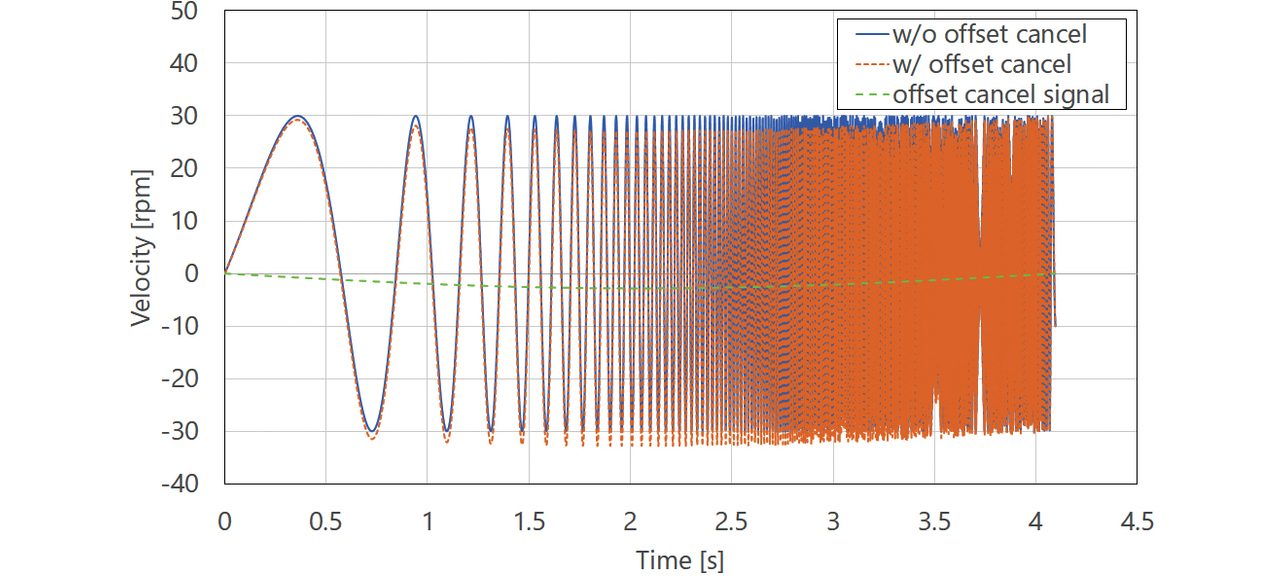
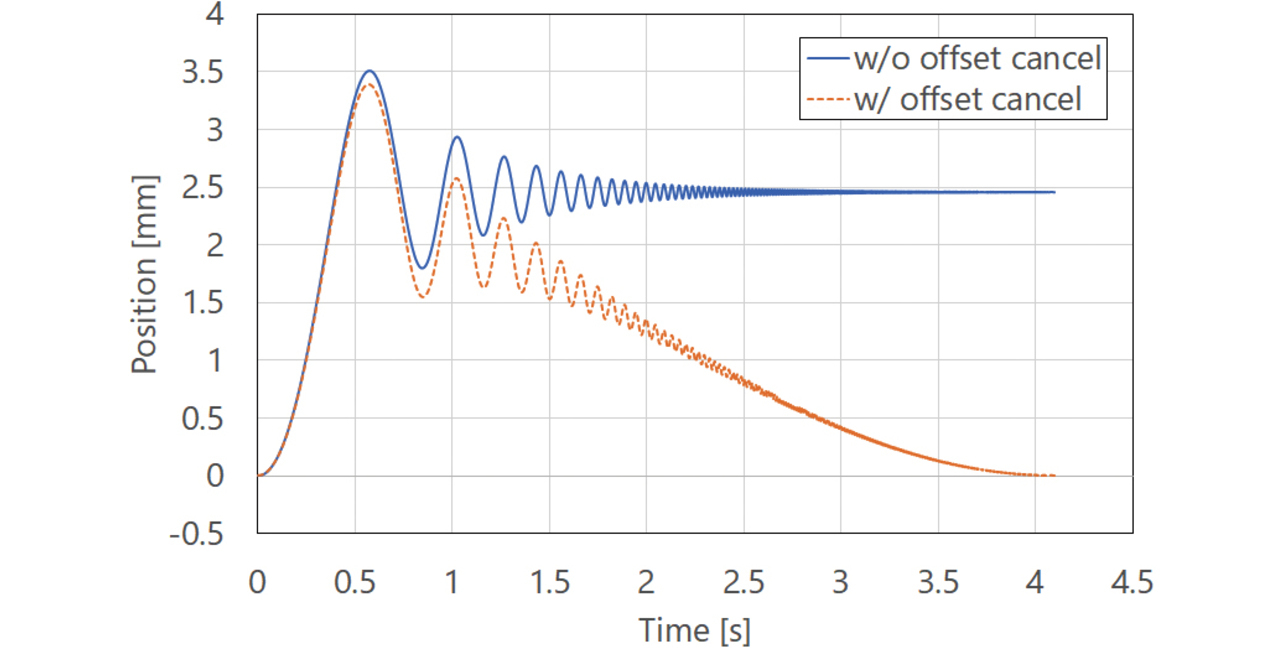
そこで、本提案手法では、加振完了位置が加振開始位置に戻る対策を講じた。具体的には、SweptSineの加振波形により生じる位置オフセットをキャンセルするように低周波正弦波を重畳した。図12に点線(w/ offset cancel)で低周波正弦波を重畳したSweptSine波形、図13に点線(w/ offset cancel)でそのときの位置応答をそれぞれ示す。
重畳する低周波正弦波の同定方法を以下に示す。(3)式のように振幅を

重畳前のSweptSine波形によって生じる位置オフセットをL、総加振時間を

同定が煩雑になることを防ぐため、生じた位置オフセットとは反対の一方向のみに移動する速度正弦波を重畳する。このとき重畳する正弦波は半周期が加振時間 

(5)式を(4)式に代入して整理すると、(6)式から振幅 

(5)、(6)式を(3)式に代入すると、重畳する正弦波は(7)式となる。

4. 実験結果
4.1 制御目的に応じた制御構造を選択した効果
制御目的に則した制御構造を採用することの効果を示すために、位置決め時間の最小化を目指す実験と、軌道追従誤差の最小化を目指す実験を実施し、制御構造の違いによる実現性能の差を比較した。前者の実験では図14に示す円盤負荷装置、後者の実験では図15に示すボールねじをそれぞれ用いた。比較したのは、モデル追従制御構造(Model Following Control)と100%フィードフォワード制御構造(100% Feed Forward)の2方式である。


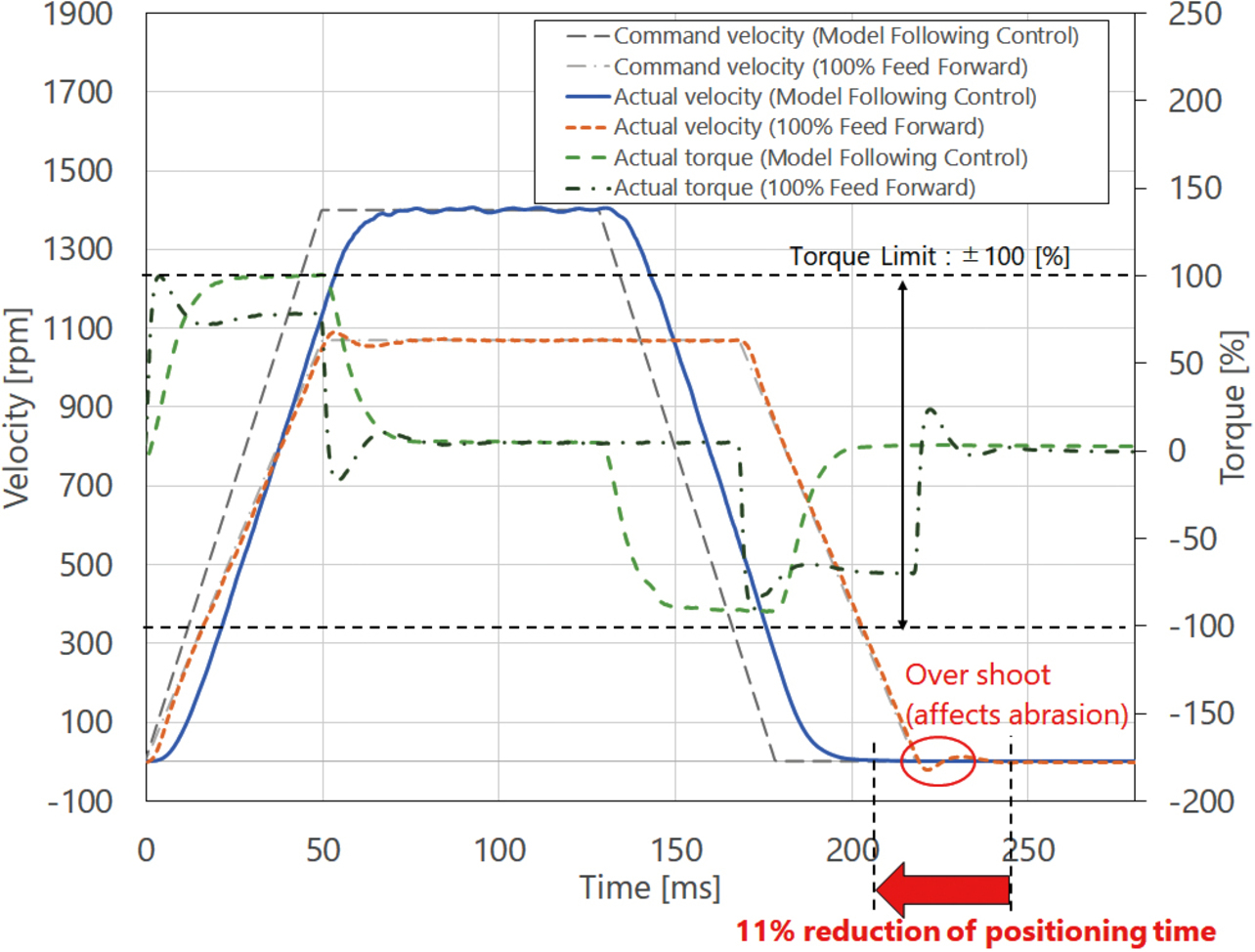
図16は制御構造の違いによる位置決め時間の違いを示すもので、各制御構造においてトルクが出力制限を超えない範囲で実現可能な最速の目標軌道を与えている。表1に実験条件を示す。モデル追従制御では、目標軌道と内部指令値に乖離が発生する。その一方で、オーバーシュートを抑制することができ、装置へのダメージを減らせる。また、トルク飽和を抑制できるので最大速度を大きく設定することが可能になる。その結果、100%フィードフォワード制御構造に対して、位置決め移動時間を11%短縮できている。
| 条件項目 | 値 |
|---|---|
| 最大速度(モデル追従制御) | 1070 rpm |
| 最大速度(100%フィードフォワード制御) | 1400 rpm |
| 加減速時間 | 50 msec |
| 移動距離 | 3 revolutions |
| トルク出力制限 | ±100%(±0.318 N.m) |
| Advanced Auto-Tuningの調整強度 | Middle |
図17は制御構造の違いによる目標軌道への追従性の差を示すもので、目標軌道との誤差を200倍拡大したものを目標軌道に加算した誤差円で示している。図18は追従誤差が最大となる象限突起部6)の拡大図である。表2に実験条件、表3に制御構造毎の目標軌道との平均誤差、最大誤差をそれぞれ示す。表3から、目標軌道から推定した必要トルクをフィードフォワードで与える100%フィードフォワード制御構造の方が、モデル追従制御より42%追従誤差が小さいことが分かる。このことから、目標軌道に対するローパスフィルタ効果があるモデル追従制御構造は、目標軌道追従性重視のアプリケーションには適していないことが判る。
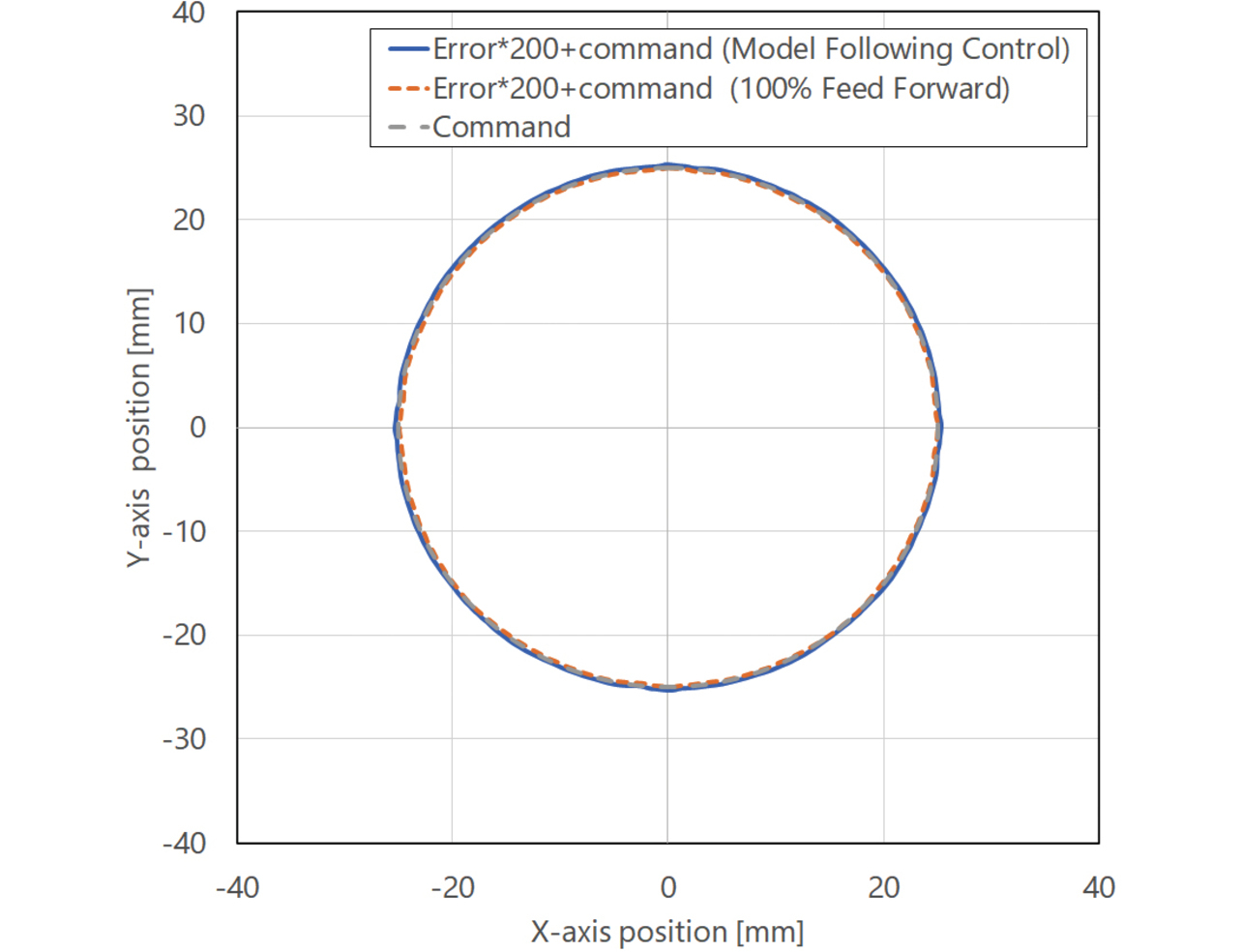
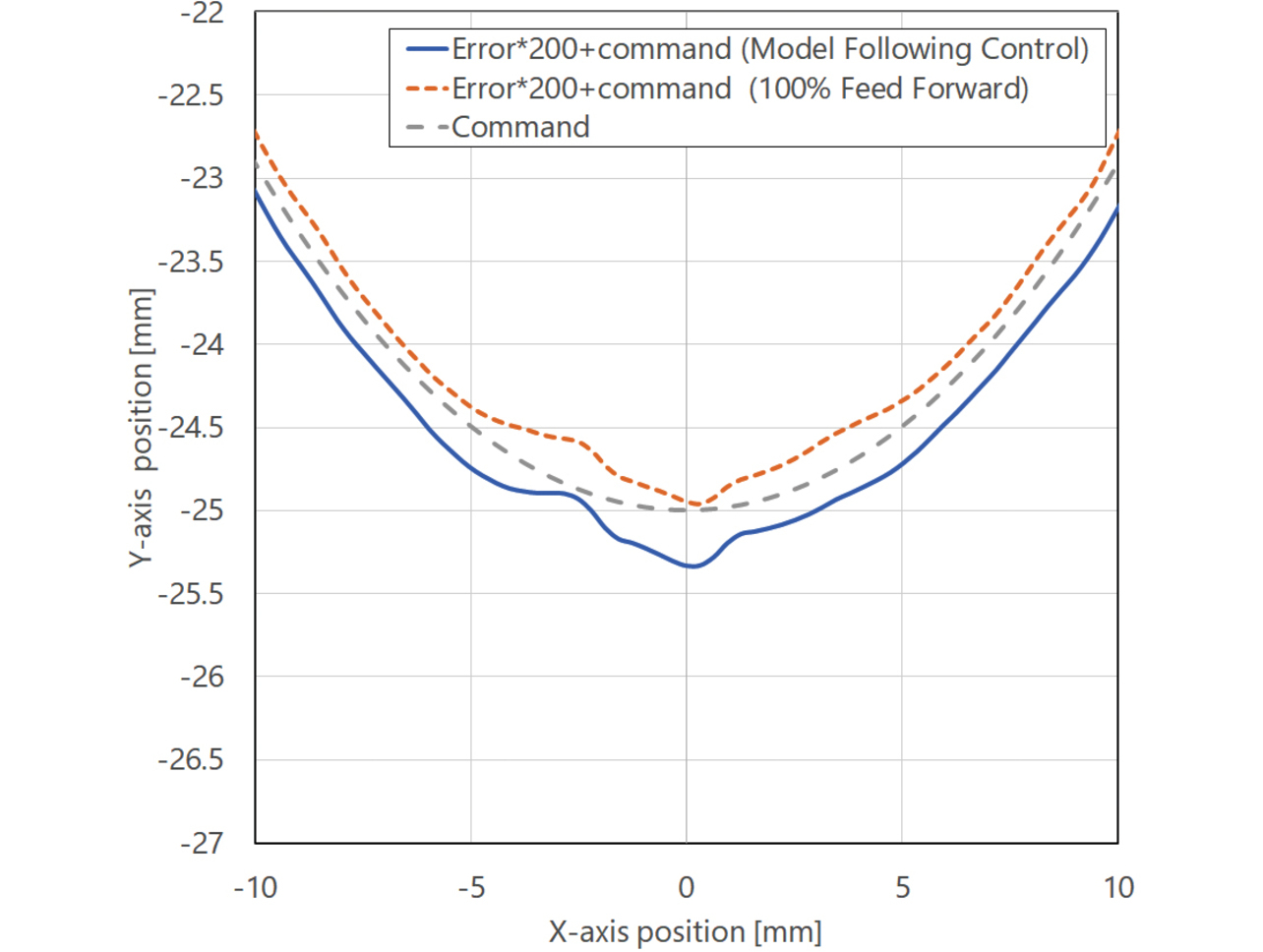
| 条件項目 | 値 |
|---|---|
| 円半径 | 25 mm |
| 移動速度 | 2π rad/s |
| Advanced Auto-Tuningの調整強度 | Middle |
| 目標軌道との誤差 | モデル追従制御 | 100%フィード フォワード制御 |
|---|---|---|
| 平均誤差 | 1.1 μm | 0.7 μm |
| 最大誤差 | 4.1 μm | 2.4 μm |
4.2 安定性解析に基づく調整の効果
図19に従来の時間応答波形に基づくゲイン調整方法(Easy Tuning)と、本手法(Advanced Auto-Tuning)による整定時間の比較結果を示す。Easy Tuningの制御構造、目標整定時間は何れもデフォルト値とし、それぞれ「モデル追従制御」、「50 ms」とする。本手法での制御目的は、「位置決め時間重視」、調整強度は「Middle」とした。その他の実験条件は表4に示した。制御構造はどちらもモデル追従制御構造で差はない。本手法ではフィードバック系の安定性を定量的に評価しながら、フィードバックゲインを上昇させて制御帯域を拡大する。このことで、Easy Tuningに対して90%もの整定時間の削減が行えた。
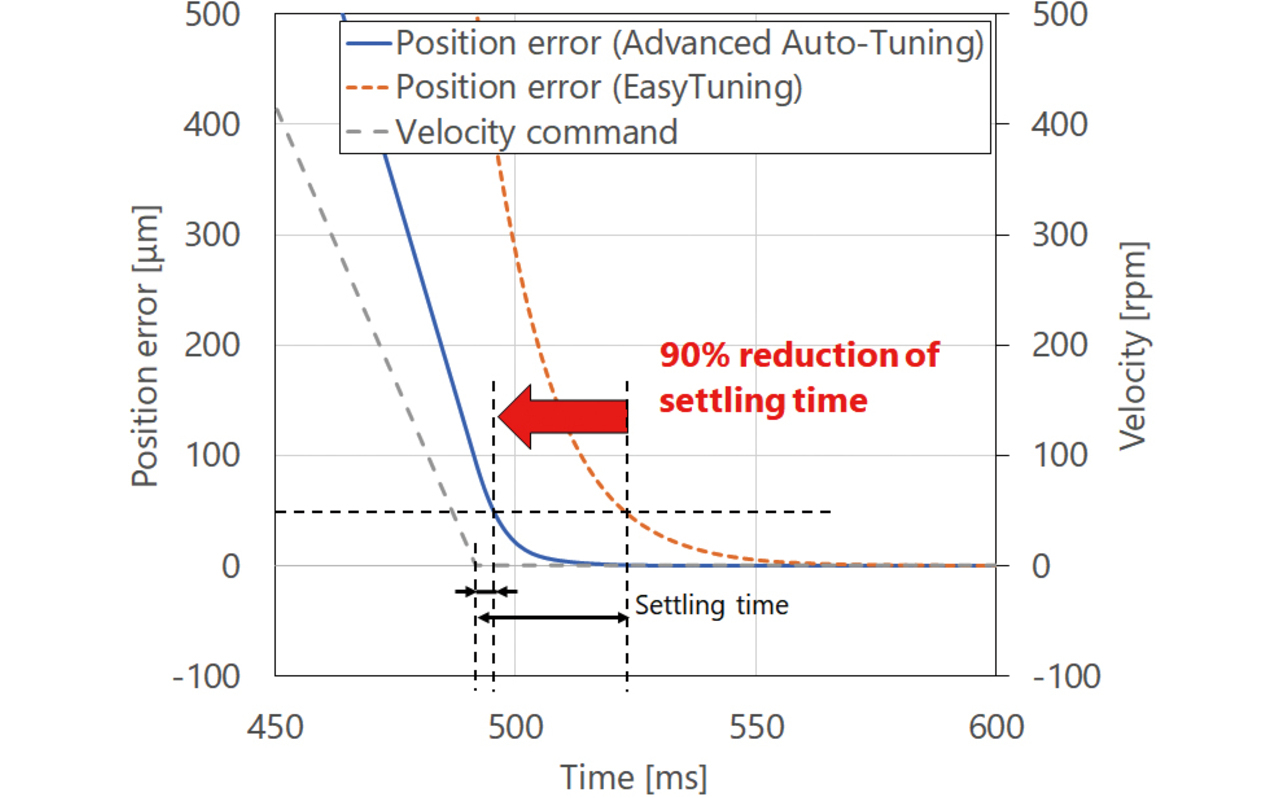
安定性解析なし:EasyTuning、安定性解析あり:Advanced Auto-Tuning
| 条件項目 | 値 |
|---|---|
| 最大速度 | 500 rpm |
| 加減速時間 | 50 msec |
| 移動距離 | 3 revolutions |
図20にEasy Tuningと本手法(Advanced Auto-Tuning)による軌道追従性の比較結果(誤差円)を示す。本手法での制御目的は「軌道追従性重視」、調整強度は「Middle」とした。その他の実験条件は、表2に示したものと同様である。本手法では、制御構造に100%フィードフォワード制御構造が選択されるため、内部的に目標軌道をフィルタリングすることは無く、またフィードフォワードトルクにより遅れ無く目標位置に動作させることが可能になる。更に、安定性を定量的に評価しながら制御帯域を最大限拡大することで、装置モデルに含まれない象限突起に対しても高速に補正動作が行える。その結果、Easy Tuningに対して98%もの軌道追従誤差の削減が行えた。
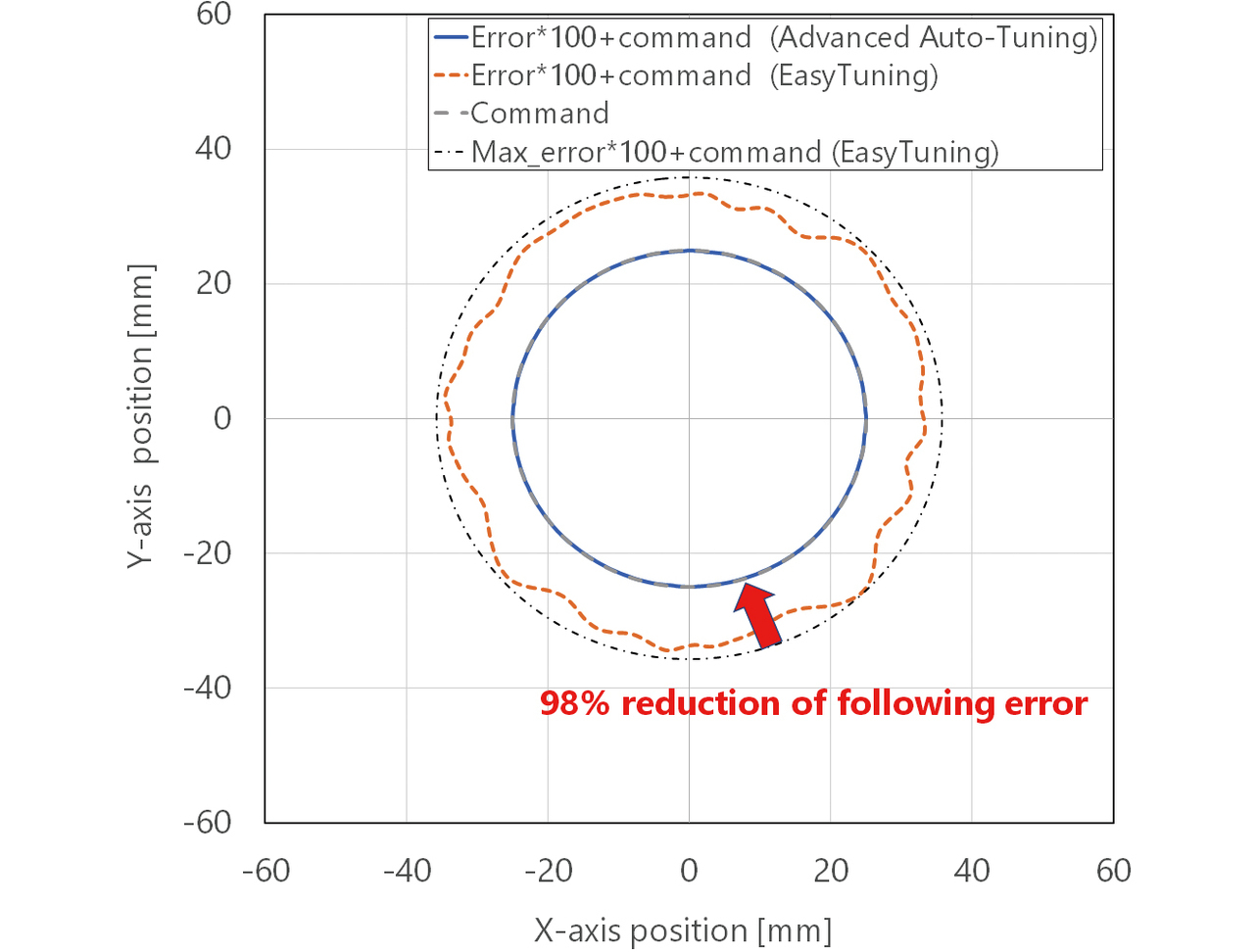
安定性解析なし:EasyTuning、安定性解析あり:Advanced Auto-Tuning
4.3 調整時動作範囲削減の効果
図21に、SweptSineの加振波形により生じる位置オフセットをキャンセルする低周波正弦波の重畳効果を示す。本提案手法(Advanced Auto-Tuning)では、調整完了までに多い場合は40回程度の装置加振試験を実施する。リードピッチ10 mmのボールねじの場合、本提案手法によらない場合、調整完了までに35 mm程度の装置移動が発生する。一方、本提案手法では、1回の加振試験での最大移動量は2.5 mm、39回加振後の位置のオフセット量は実測値で0.8 mmに抑えられた。このことは、装置が動作範囲外に移動して破損するリスクを極めて小さく抑えられ、本提案手法がオペレータの心理的負担軽減に貢献できることを意味する。
5. むすび
従来の時間応答波形に基づくサーボパラメータ調整では、十分な実現性能が得られなかったり、僅かな動作環境の変化で装置が不安定になったりするという問題がある。この問題に対して、サーボパラメータ調整の専門知識を必要とすることなく制御目的を指定するだけで装置の最大性能を引き出せるサーボパラメータ調整手法を提案した。
本提案手法では、装置を含む制御系の安定性について、周波数解析技術を用いて定量的に評価することで、実現性能と安定性のトレードオフを図っている。安定性解析には、実機だけでなくシミュレーションを活用し、装置の加振回数を削減することで調整時間の削減と装置ダメージの抑制を図った。シミュレーションを活用することで、ノッチフィルタなどのサーボパラメータの組み合わせについて、一回の加振動作で約400通りの評価が可能になり、調整の専門家であっても調整時間の制約から到達が難しい実現性能を数分で達成可能にした。更に、周波数解析の加振軌道の工夫により装置の動作範囲を数mm以内に抑制し、誤操作による装置破壊リスクと現場オペレータの心理的負担の軽減に貢献できた。尚、安定性についてフィードバックゲインを変数とする安定性マップとして見える化した。これによって、実現可能な制御帯域の限界や安定性の余裕度が直感的に把握でき、実現不可能な性能を追い求め続けることの回避や、装置の機械剛性の改善度評価に活用することが期待できる。
今後は、上記の安定性解析とシミュレーションを活用したサーボドライバパラメータ調整手法を、複数のモータが機械的に結合された装置に展開し、対応可能なアプリケーションの拡大を図っていく。
参考文献
- 1)
- オムロン, “サーボモータを調整するための制御装置および方法,” 特許第6409886号, Oct. 24, 2018.
- 2)
- オムロン, “処理装置、制御パラメータ決定方法、及び制御パラメータ決定プログラム,” 特許第6460138号, Jan. 30, 2019.
- 3)
- オムロン, “設定支援装置,” 特許第7119760号, Aug. 17, 2022.
- 4)
- オムロン, “設定支援装置,” 特許第7119761号, Aug. 17, 2022.
- 5)
- S. Manabe and Y. C. Kim, Coefficient Diagram Method for Control System Design, Springer, 2022.
- 6)
- 松原厚, 精密位置決め・送り系設計のための制御工学, 森北出版株式会社, 2008, pp. 185-198.
本文に掲載の商品の名称は、各社が商標としている場合があります。














