ヒトの動きやバイタルサインを計測する人体センシングは、計測デバイスの普及と関連サービスの拡大に伴い我々にとって身近な存在となっている。様々な計測デバイスの中でも、人体と接触せずに非接触でヒトのバイタルサインを精度よく計測できるミリ波レーダが注目されている。バイタルサインの一つである呼吸を体表面の変位としてレーダで計測した呼吸波形には、複数の反射信号の存在や周囲環境変化の影響により、実際の呼吸には存在しない不連続部が現れることがある。このような不連続性は、特に長時間の波形トレンドから健康状態を推定するうえで妨げとなり得るため、低減することが望ましい。

本論文では、波形の特徴とレーダで得られる空間情報に基づいて、推定された波形群の中から不連続性が小さくなる波形を選択する手法を提案している。ミリ波レーダを用いて複数人の呼吸波形を同時に計測する実験を行い、提案手法を用いて長時間の呼吸波形を構成した結果、不連続性を考慮しない場合と比較して波形に含まれる不連続性が低減することを示している。

1. まえがき

ヒトの動きやバイタルサインを計測する人体センシングは、急速なセンサの高度化・普及とパーソナルヘルスケアサービスの拡大に伴い、我々の生活において身近な存在となっている。例えばスマートウォッチに代表されるウェアラブルデバイスで心拍数、血中酸素飽和度や皮膚温度などを計測し、ストレス状態や睡眠パターンと紐づけて心身状態を日常的にモニタリングすること^1,2）が広く行われている。また、カメラを用いた自動車ドライバーの覚醒状態判定^3）や、対象物を立体として認識できる深度センサを用いたヒトの運動・姿勢計測^4）といった応用も進められている。こうしたことから、人体センシング技術の重要性は、医療・ヘルスケアや労働安全の分野において、今後ますます高まることが期待される。

一方で普及が進むこれらの計測手段には、実用上の懸念点も存在する。例えばウェアラブルデバイスなどの接触型センサは、計測中常にユーザの皮膚に接触させる必要がある。そのため、長時間にわたる計測では不快感を覚えたり、アレルギーを持つユーザの場合は皮膚炎を生じたりすることがある。カメラなどの光学センサでは、センサに接続される通信ネットワークを介して顔画像などの個人情報が流出し、ユーザのプライバシーを侵害するおそれがある。

このような懸念に対応する手段として、レーダなど電波を用いた人体センシング技術が注目されている。電波を用いた計測は、一般に身体とは非接触で行うため、センサの装着に関する様々な課題から解放される。また、ヒトの顔を識別できるほどの空間分解能を持たず、プライバシーに関する懸念も小さい。電波の中でもマイクロ波やミリ波は着衣を透過し、ヒト体表面の動きを捉えることができる。とりわけミリ波を送信信号として用いるミリ波レーダは、その波長の短さと信号の広帯域性に基づく、微小変位に対する精度の高い計測手段として注目されており、ヒトの呼吸や心拍を計測対象とした様々な検討が行われている^5-7）。

呼吸に伴う換気量の推移や体表面の微小変位を時間波形として表した呼吸波形は、呼吸の深さや吸気・呼気の時間比率などの情報を含んでおり、睡眠や健康の状態を推定する手段として有用である^8,9）。レーダを用いて呼吸波形を計測するとき、後述するように、計測の繰り返し周期として数秒から数十秒の時間区間（以下、観測区間）を設定することがよく行われる^5-7）。数分以上の連続波形を得るには、数秒から数十秒単位の各観測区間で推定した波形同士を接続することになる。健康や睡眠の状態変化を把握するには、数分以上の単位で呼吸を観察することが有効である。しかし、従来の報告は単一の観測区間における計測結果を扱うものが殆どであり、複数の観測区間において波形を接続するときの整合性は考慮されていない。その結果、波形の接続部である観測区間境界において不連続性を生じることがある。これは実際の呼吸には存在しない成分であり、波形をもとに様々な推定をするときの妨げとなり得るため、低減することが望ましい。

本論文では、連続呼吸波形に含まれる不連続性を小さくするための、各観測区間における波形選択手法を提案する。2.でレーダを用いた呼吸波形計測の原理について述べ、3.では不連続性の評価指標を導入する。4.で提案手法の詳細について述べ、5.ではミリ波レーダを用いて計測した複数観測区間の波形群から提案手法を用いて波形を選択し、連続波形を構成したときの不連続性の評価結果を示す。

2. レーダを用いた呼吸波形計測

2.1 信号モデル

簡単のため、連続波（Continuous Wave: CW）方式のレーダにおいてアンテナを送受信共用とし、ヒトの体表面における電波の反射が一点のみで生じる場合を考える。このとき、送信信号が体表面で反射され、アンテナで受信される受信信号を直交検波して得られるベースバンド信号は次のように表せる^10）。

（1）

ここでtは時間、Aは複素振幅、f₀は送信信号の周波数、d(t)は呼吸に伴うレーダ視線方向の体表面変位、cは光速、s_DCは静止物からの反射波などに相当する静止クラッタと呼ばれる直流成分、n(t)は雑音である。上式からわかるように、体表面変位成分が位相項 に含まれており、その位相変化量は周波数に比例する。同じ体表面変位に対して周波数が高いほど位相変化量が増大するため、呼吸に伴う微小変位については、ミリ波を用いることでマイクロ波よりも感度の高い計測が可能となる。いま、Albaneseらの研究^11）から、d(t)を次のように定式化する。

（2）

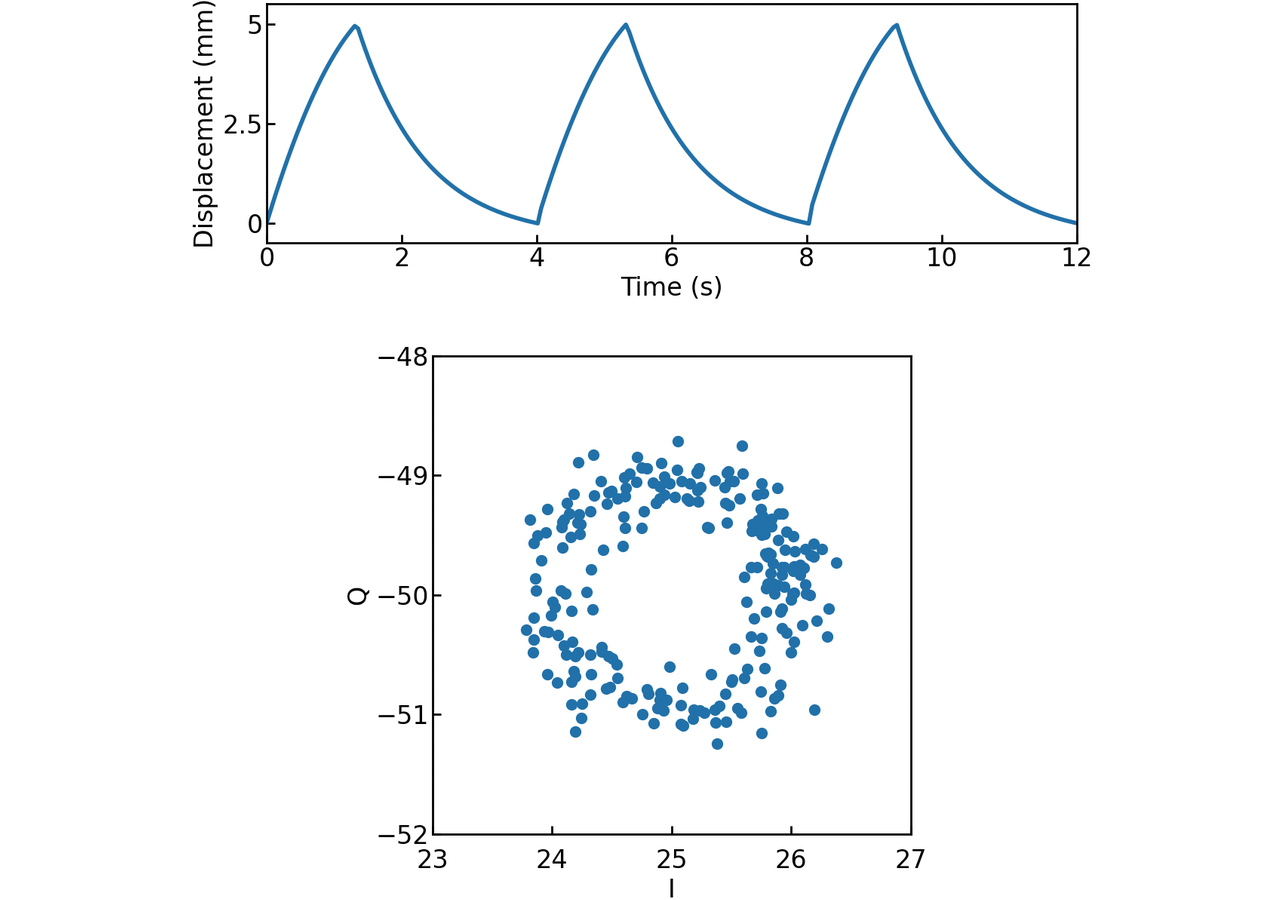
ここでKは変位量を表す係数、T_Iは呼吸周期における吸気時間、T_Eは同呼気時間、T＝T_I + T_Eは呼吸周期、τ は呼気における時定数である。例として、式（2）において体表面変位のピークトゥピークをK＝0.005（5 mm）、呼吸周期をT＝4 s、吸気と呼気の時間比率をT_I: T_E＝1:2と仮定し、式（1）に代入してベースバンド信号を求める。ただし式（1）においてf₀＝60 GHz、|A|＝1、s_DC＝25–50j、信号対雑音比を12 dBとし、信号は周期50 msでサンプリングされた離散時間信号であるとする。

図1上は上記で設定した体表面変位の時間波形、図1下はそれに対して求めたベースバンド信号を複素平面上でプロットしたものである。信号は、複素平面上で静止クラッタ成分を中心とした円弧を描くことがわかる。この性質を利用し、円フィッティングなどで推定した円の中心を基準とする信号偏角から位相（体表面変位成分）を求め、呼吸波形を推定する逆正接復調と呼ばれる手法が提案され広く用いられている^12,13）。この手法では、円の中心を正確に推定できなければ波形に歪みが生じる。そのため、クラッタの経時変化が大きい場合には計測精度が低下することに注意する必要がある。

2.2 複数信号の分離

前節で扱った理想的な反射信号に対し、実際の反射信号について考える。体表面における電波の反射は人体の様々な部位において同時に生じ得るため、反射信号は一つだけでなく複数受信されることが普通である。さらにレーダの計測エリア内に複数のヒトが存在すると、異なる呼吸に対応した体表面変位成分が信号に重畳する。各々の呼吸波形を精度よく計測するためには、適切に信号を分離・推定することが必要である。その手法は様々であるが、本論文ではレーダと反射点間の距離や反射信号のアンテナ入射角推定結果に基づいて信号を空間的に分離する手法をとる。ミリ波レーダでは、周波数変調した送信信号を用いて距離推定を行う周波数連続変調波（Frequency Modulated Continuous Wave: FMCW）方式による広帯域信号の送受信や、複数の送受信アンテナを用いて仮想的なアレーアンテナを形成し方位推定性能を高める多入力多出力（Multiple-Input Multiple-Output: MIMO）レーダ技術を採用することで、センチメートルオーダの空間分解能を実現できる^14）。

2.3 観測区間における呼吸波形計測

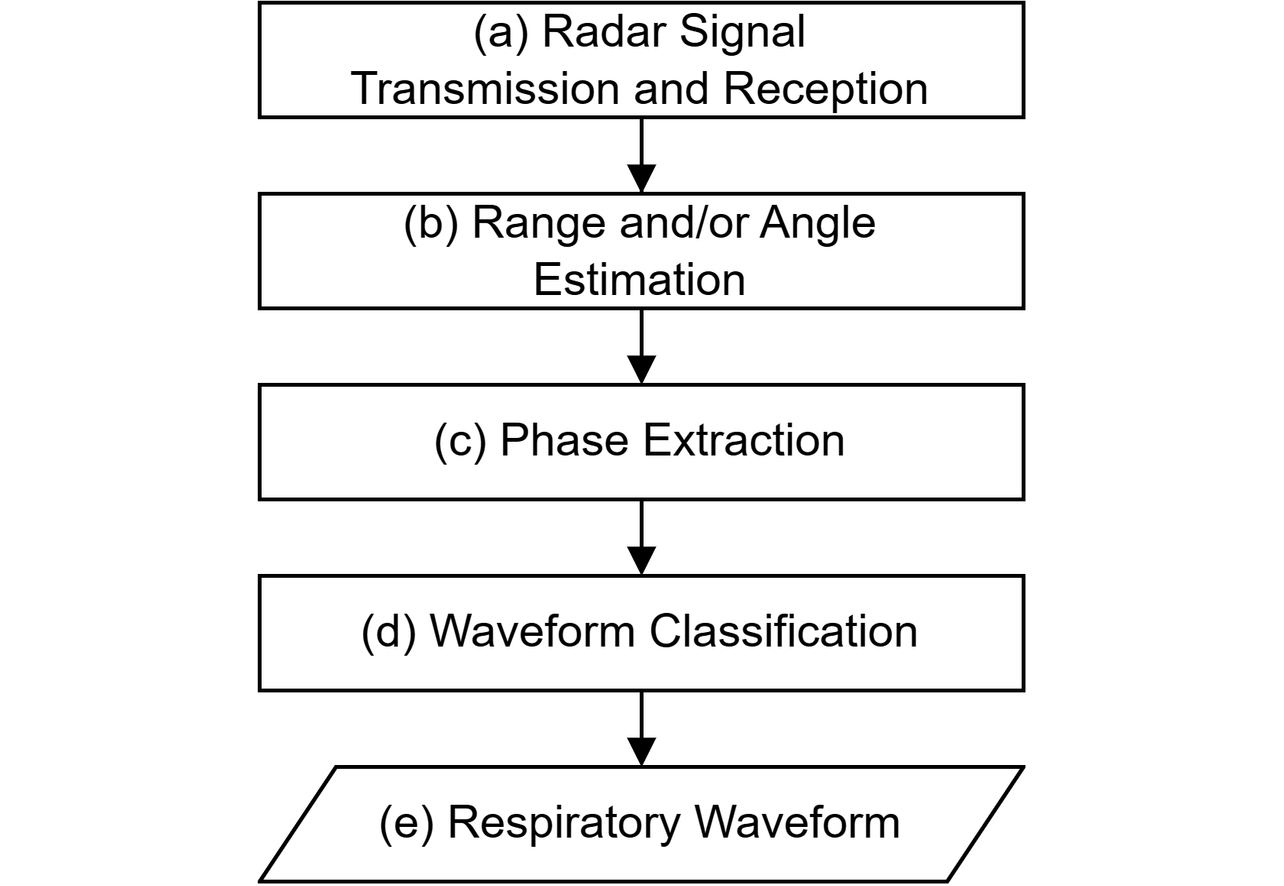
呼吸波形計測で行われる信号処理について説明する。図2はレーダを用いた呼吸波形計測の、観測区間における信号処理フローの一例を示している。はじめにレーダ信号の送受信を行う（図2（a））。反射信号を空間的に分離するため、得られたベースバンド信号をもとに距離や方位に対する空間プロファイルを求める（図2（b））。これらの計算にはフーリエ変換がよく用いられ、計測空間を距離や方位方向に離散的にサンプリングして得られる空間上の各点をビン（bin）と呼ぶ。各ビンは振幅と位相からなる複素振幅のデータを持つ。レーダ信号送受信と空間プロファイル算出は所定周期で繰り返し行う。後に推定する波形のエリアシングを防ぐため、空間プロファイルの算出周期は想定される呼吸周期に対して十分短くなるように設定する。

次に観測区間が終了するまで空間プロファイルを蓄積してから、各ビンの時間方向データに対して静止クラッタを推定・除去して逆正接復調を行う（図2（c））。想定される呼吸周期よりも観測時間を長く設定することで、波形に含まれる（準）周期性の検出が容易になる。一方で数分以上の長い観測区間を設定すると、周囲環境やヒトの位置が経時変化することで歪んだ波形が推定され、長時間にわたり正確な計測結果が得られなくなるという課題がある。また、観測区間が長くなるほど信号処理対象のデータサイズと計算規模が増大し、計測システムのコストアップにつながる。そのため、観測区間は数秒から数十秒程度に設定されることが多い。

その後、各ビンで得られた波形が呼吸に由来するものであるかを判定し、呼吸と相関があると考えられた信号成分が含まれるビンを抽出する（図2（d））。呼吸周期に対応したバンドパスフィルタの適用や、クラスタリングによる分類など様々な手法が提案されている^5-7）。ここで得た波形（群）をもとに、観測区間における出力として代表となる波形を構成する（図2（e））。

3. 呼吸波形の不連続性と評価指標

3.1 呼吸波形に含まれる不連続性

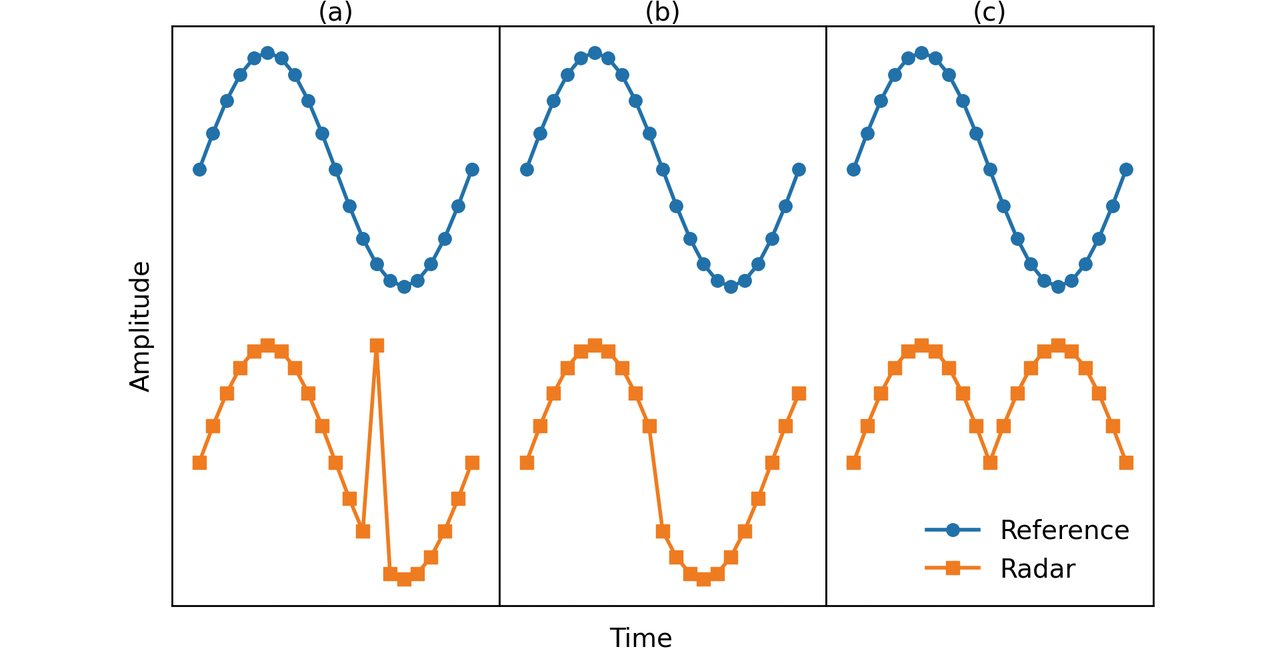
呼吸波形に含まれ得る不連続性の一例を図3に示す。図中ではレーダで推定した波形と、フローセンサやベルト型センサ（以下、呼吸ベルト）など信頼性の高い他の計測手段を用いて得た波形（以下、リファレンス波形）を併せて示している。ここで各波形は、離散時間信号としてサンプリングされているものとする。図3（a）は、単一のサンプリング点でスパイク状の応答が得られた場合に相当する。計測中に何らかの外乱が混入することや、波形の歪みなどで生じる。図3（b）は、ある時点（例えば観測区間の境界）を境に波形がオフセットした、あるいは位相差が生じた場合を示している。こうした現象が起きるのは、2.で述べたように、受信信号に含まれる静止クラッタの推定精度は経時変化などによって観測区間ごとに変化し得るため、各観測区間で異なった歪み成分が波形に重畳することなどによる。また、体表面における反射信号が空間分解能やビンの空間上の広がりよりも狭い範囲で複数得られることや、反射信号が複数の伝播経路を経るマルチパスにおいて、レーダとヒトの位置関係の僅かな変化に伴い状態が変化することも原因になり得る。たとえ同一ビンであっても、支配的となる信号成分が経時変化することで推定される波形は観測区間前後で変化し得る。図3（c）は、ある時点で波形の位相が反転した場合を示している。これは、レーダで推定した波形がレーダ視線方向の体表面変位を反映していることに起因する。特に送信波が体表面に対して浅い角度で入射すると、変位方向と視線方向が直交するようになり、ヒトの部位形状によってはレーダから見て互いに逆方向の変位成分が同時に計測されることもある。また、我々の観察によると、人によっては呼吸時に腹部と胸部が互いに逆方向に変位することがしばしば生じる。この場合、送信波が体表面に対して垂直に近い角度で入射したとしても、同相・逆相の関係にある波形が得られる。

3.2 不連続性の評価指標

呼吸波形に含まれる不連続性の低減について検討するため、不連続性の大小を定量的に評価する指標を導入する。波形は呼吸の状態に応じて様々な傾きをとるため、単に隣接するサンプリング点間の値の変化量だけで不連続性を評価することは適切でない。そこでリファレンス波形との値の差に注目する指標（以下、差の指標）と、波形傾きの変化に注目する指標（以下、傾きの指標）という観点の異なる二つの指標を導入する。なお、本論文では特に観測区間境界の不連続性に注目するが、スパイク応答状の不連続性は境界以外でも生じ得るため、観測区間境界以外も含む波形中の全てのサンプリング点を不連続性の評価対象とする。また、以降の議論において、各観測区間内の波形はN個の離散点n＝1, ..., Nを用いて等時間間隔でサンプリングされているものとする。

3.2.1 差の指標

隣接するサンプリング点間の差分値を、リファレンス波形とレーダで推定した波形とでそれぞれ求める。それらの差の絶対値を求めたものが差の指標であり、式（3）のように表される。ここで は、現在の観測区間で指標計算対象となる波形のn番目のサンプリング点における変位推定値である。ただし は、直前の観測区間で指標計算対象となる波形のN番目のサンプリング点における変位推定値を指すものとする。サンプリングタイミングは両波形とも共通とし、値の比較を容易にするため標準化によってスケーリングする。この指標では両波形の形状が近しいほど指標値が小さくなり、不連続性が小さいと見做される。ただし、同じ呼吸を対象に計測したとしても、計測原理の違いによって得られる波形が異なる場合がある。レーダは呼吸に伴う体表面変位から波形を得ているが、例えばフローセンサは呼吸に伴う気流変化から波形を得ており、計測原理が全く異なる。レーダと計測原理が大きく異なる手段でリファレンス波形を取得すると、図3に示したような不連続部がレーダの推定波形に含まれていなかったとしても、指標値が大きくなり不連続性が大きいと見做される可能性があることに注意が必要である。

（3）

3.2.2 傾きの指標

傾きの指標は、レーダで推定した波形において評価対象となるサンプリング点前後の傾きの平均値と、サンプリング点における傾きの差の絶対値を求めたものであり、式（4）のように表される。ここで は現在の観測区間で指標計算対象となる波形のn番目のサンプリング点における後方差分で求めた傾きである。ただし は直前の観測区間で指標計算対象となる波形のN番目のサンプリング点における後方差分で求めた傾き、 は直後の観測区間で指標計算対象となる波形の1番目のサンプリング点における後方差分で求めた傾きを指すものとする。差の指標と同様に、標準化でスケーリングした波形を対象とする。この指標は傾きの変化率を反映しており、変化率が小さい滑らかな波形形状であれば指標値が小さくなり不連続性が小さいと見做される。一方で指標の算出にリファレンス波形が関与しないため、リファレンス波形と大きく形状が異なる波形が推定されたとしても、不連続性が小さいと見做される可能性もある。

（4）

3.3 指標の検証

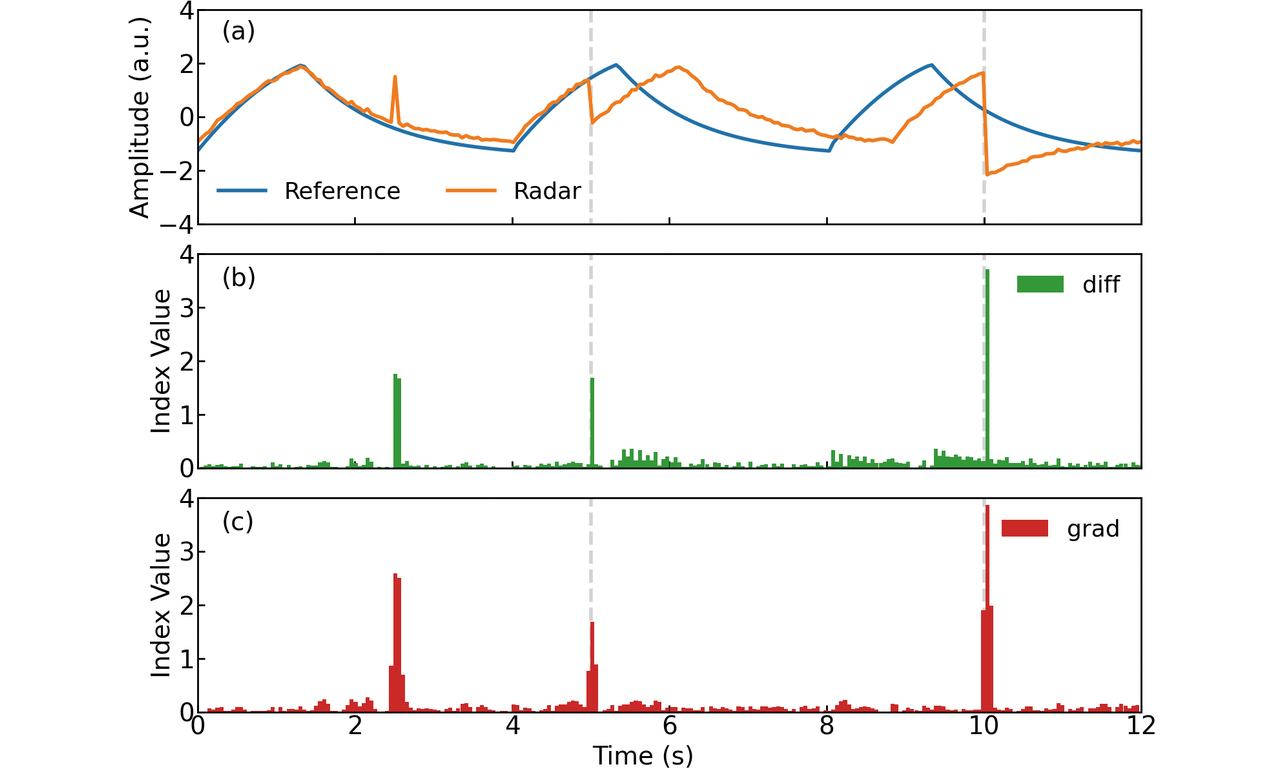
上記の評価指標が機能することを確認するため、シミュレーションを行う。リファレンス波形とレーダに関する設定は2.で述べた条件に基づくものとし、観測区間長は5 sとする。図4（a）は評価対象となるリファレンス波形と、レーダで推定した呼吸波形を示している。両波形は標準化でスケーリングしている。図中の破線は観測区間境界を表している。いま、レーダで推定した波形において観測区間の1周期目2.5 s時点にスパイク応答、2周期目にリファレンス波形に対して呼吸周期5分の1相当の位相差、3周期目にリファレンス波形に対して逆相となる不連続部を与えている。この波形について差の指標値を求めたものが図4（b）、傾きの指標値を求めたものが図4（c）である。両指標ともに、不連続部では指標値が相対的に大きく、それ以外では小さくなっている。両指標が機能することを確認できたため、これらを用いて不連続性の評価を行うこととした。

4. 波形選択手法

前述したように、一般にレーダでは複数の反射信号が同時に受信されるため、呼吸に対応した成分を持つ波形も同様に複数得られる。各観測区間で推定した呼吸波形群をもとに長時間にわたる不連続性の小さい連続波形を構成するには、それら波形群の中から適切な波形を何らかの手法によって選択する必要がある。これは図2の信号処理フローにおいて、同図（d）と同図（e）の間の処理として実行される。なお、波形をリアルタイムに連続出力するためには逐次的な処理が必要となる。そこで以降の説明では、図5に示すように直前の観測区間において波形群が既に選択済みという前提で、現在の観測区間における未選択の波形群の中から1つ以上の波形を選択する場合の手法について考える。本論文では、上記二つの波形群の情報を利用して、差（difference）・傾き（gradient）・ビン（bin）というそれぞれ異なる基準を用いて波形を選択する、三つの手法を提案する。

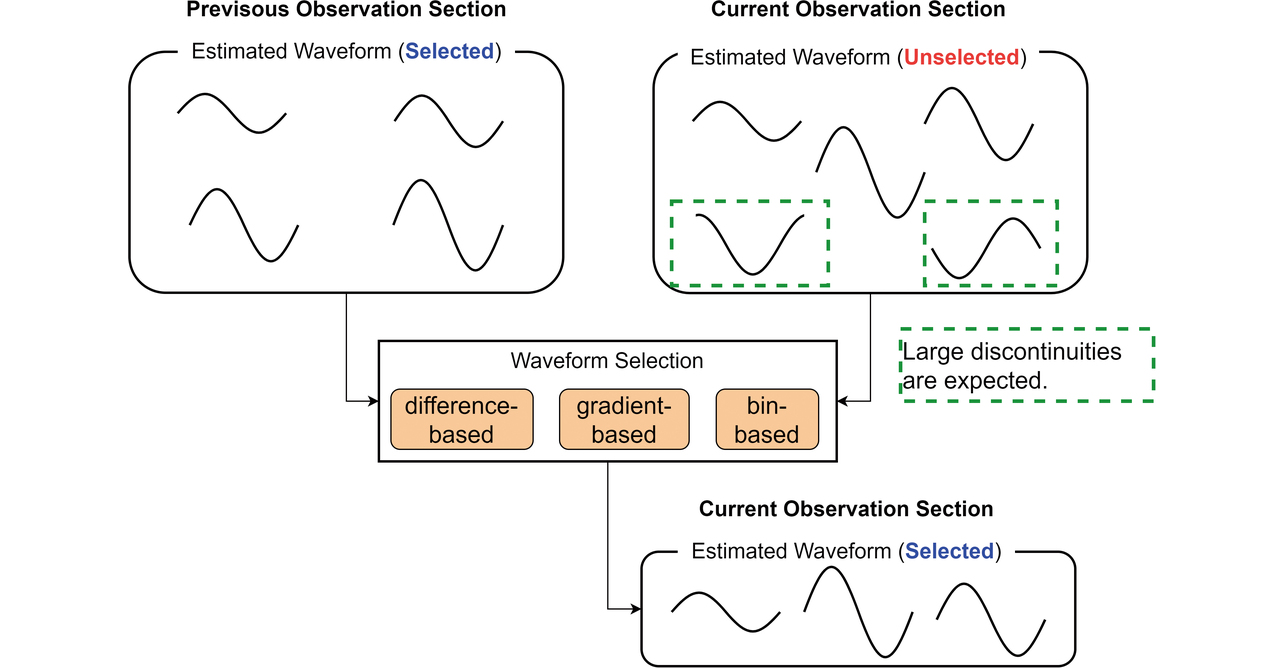
4.1 差による選択基準

現在の観測区間sにおいて推定したM_s 個の呼吸波形群について、i個目（i＝1, ..., M_s ）の波形の1番目のサンプリング点における変位推定値を とする。同様に、直前の観測区間 において推定した 個の波形群について、j個目 の波形のN番目のサンプリング点における変位推定値を とする。現在の観測区間におけるi個目の波形の変位推定値について、観測区間境界における直前の観測区間の波形群の平均変位推定値との差を式（5）のように求める。この値について昇順にソートすると、各観測区間の波形同士を接続したとき、観測区間境界前後で値の変化が小さくなるような波形が上位となることが期待される。計測条件に応じて適切な波形選択数を設定し、その数だけ上位の波形を選択する。

（5）

4.2 傾きによる選択基準

直前の観測区間において推定した呼吸波形群について、j個目の変位推定波形のN番目のサンプリング点における後方差分で求めた傾きを とする。同様に、現在の観測区間において推定した波形群について、i個目の変位推定波形の2番目のサンプリング点における後方差分で求めた傾きを とする。これらの平均値と、同じくi個目の変位推定波形の1番目のサンプリング点における後方差分で求めた傾き との差を、 にわたって平均したうえで式（6）のように求める。ここで は、観測区間境界前後の変位推定値を用いて求める。この値について昇順にソートすると、各観測区間の波形同士を接続したとき、観測区間境界前後で波形傾きの変化が急峻でない、滑らかな波形が上位となることが期待される。差による選択基準と同様に、設定した波形選択数だけ上位の波形を選択する。

（6）

4.3 ビンによる選択基準

呼吸に伴う体表面変位は、皮膚で繋がった複数の部位が連動して生じる。そのため、空間的に近い部位同士での反射信号には相関の高い体表面変位成分、つまり互いに形状の近い呼吸波形が含まれ得ると考えられる。また、レーダでの計測が困難となる大きな体動が生じなければ、同一部位からの反射が得られる空間座標は、隣接する観測区間において同じであるか、大きく変化しないことが期待できる。この仮定に基づいて、波形が得られた空間プロファイルにおけるビンの分布から基準となるビンを決定し、基準ビンとより近い距離にあるビンから得られた波形を選択する。基準ビンは、直前の観測区間において推定した波形群について、j個目の波形が得られたビン の集合

（7）

に対して、集合内のビンが対応する空間座標の中央値となる座標に対応するビン とする。現在の観測区間において推定した波形群について、i個目の波形が得られたビン と基準ビンとのユークリッド距離を次式のように求める。

（8）

この値について昇順にソートし、他の選択基準と同様、設定した波形選択数だけ上位の波形を選択する。本手法では、空間座標に基づいて波形が選択されるため、観測区間の境界における波形の値そのものは考慮されない。また、ビンの情報が存在しない、距離方向や方位方向の信号分離能力を持たないレーダを用いて計測を行う場合には適用できないことに注意が必要である。

5. 実験評価

不連続性評価指標を用いて、呼吸波形に含まれる不連続性の低減効果について検証した。具体的には、ヒトを対象にした呼吸波形計測実験を行い、提案手法の適用有無による波形不連続性への影響を評価した。

5.1 実験環境

送信信号の中心周波数を62 GHz、帯域幅を3.3 GHzに設定したFMCW方式のミリ波レーダを用いる。送信2素子、受信3素子のアンテナを備え、MIMOアレーとして素子間隔が0.5波長である6素子のリニアアレーアンテナを形成する。レーダ（空間プロファイル）サンプリング周期は80 ms、観測区間長は20 s（サンプリング点数N＝250）である。図6は実験における被験者とレーダの配置関係を示している。家庭における家族の就寝シーンを想定し、被験者は3名（A, B, C）として、仰向けの状態で肩を接するように0.45 m間隔で横並びに配置する。レーダは被験者頭側、中央の被験者Bが正面に来るように設置し被験者胸部からの水平距離を0.5 m、設置高さを被験者背面からの垂直距離を0.3 mとする。レーダの計測と同時にリファレンス波形を取得するため、呼吸ベルトを各被験者の体幹に装着する。レーダと呼吸ベルトは、体表面の変位を捉えて呼吸波形として表すという点で共通しており、理想的には両者の波形は高い相関を持ちうる。呼吸ベルトのサンプリング周期は10 msである。レーダのサンプリングタイミングと同期させることで、共通のサンプリング点において両者の値を比較できるようにする。

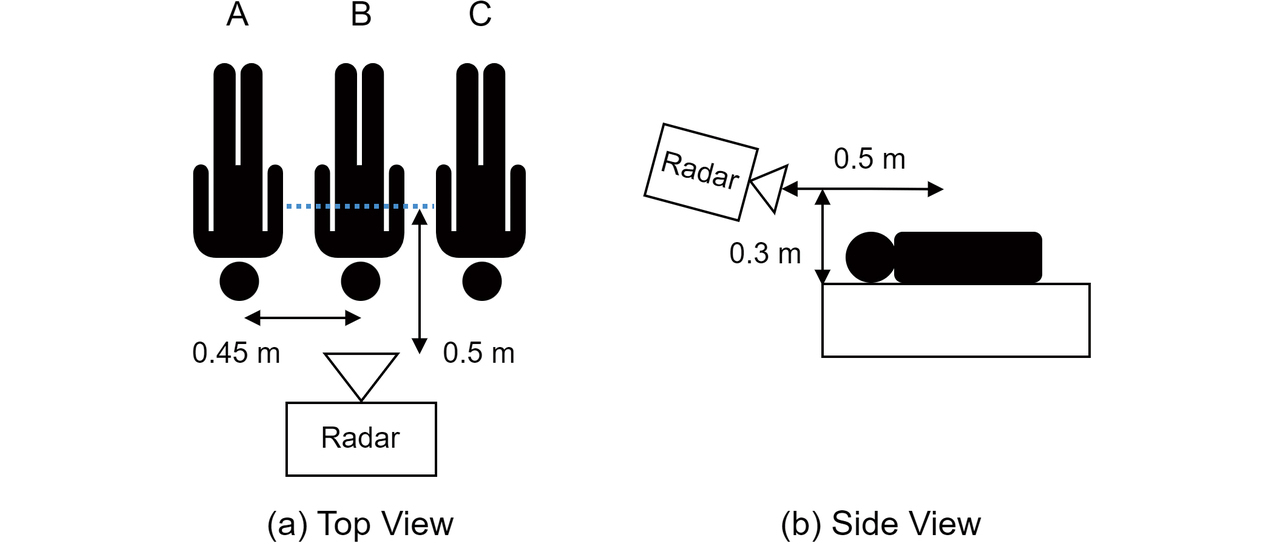
以上の構成により、各被験者の呼吸波形を連続的に計測した。観測区間30周期分に相当する600 sにわたる計測結果を対象として、時系列クラスタリング^15）を用いて各観測区間で被験者ごとに呼吸波形群を抽出した。提案手法における波形の選択数は、各観測区間の計測条件に応じて適応的に設定することで、波形不連続性の低減効果が高まることが期待される。その点は今後の課題とし、今回は全観測区間で共通の波形選択数とした。そのために、全観測区間のうち得られた波形数が最も少ない区間の波形数を、提案手法における波形の選択数として設定した。これをもとに、各観測区間で提案手法を用いて波形を選択した。

5.2 評価結果

提案手法を用いて各観測区間で波形を選択し、全観測区間にわたる連続呼吸波形を構成した。連続波形は、各観測区間で選択した波形群の各サンプリング点における中央値から構成した。このときの、各観測区間境界のサンプリング点における不連続性指標の平均値を表1に示す。なお、比較対象として設定した選択基準なしの場合では、各被験者に対応した波形群を抽出するクラスタリングの過程において、ビンに対して一意に付与されるインデックスに基づき昇順に選択している。これは信号処理の過程で副次的に得られるものであり、不連続性の低減を意図したものではない。

表1から、提案手法を用いることで、元々不連続性が小さい被験者Bを除き不連続性が低減されていることがわかる。また、三つの提案手法の間では指標値の差が小さく、いずれも観測区間境界の不連続性低減に対して同程度の効果が得られた。被験者Bのみ指標値が変化しなかった理由として、レーダの正面に位置しているため、正面方向で信号分解能が高くなるという方位推定の性質によって、適切に空間分離された信号が毎回の観測区間で得られ易かったことや、後述するマルチパスによる反射信号が比較的少なく、波形の歪みが小さかったことなどが考えられる。

表2は連続波形を構成したときの、観測区間境界を除くサンプリング点における不連続性指標の平均値を示している。観測区間境界の場合と同様に、提案手法を用いることで不連続性が低減されている。3.1で述べたように、各波形に重畳する歪み成分は異なっている。歪みが比較的大きい波形は瞬時的に変位推定値が大きく変化し得る。そのため、歪みが小さい波形と比較して、差・傾きの選択基準において不連続性が大きいと見做される可能性が高くなる。歪みが大きい波形が選択されなくなることで、観測区間境界以外においても指標値が小さくなり、不連続性が低減される。また、各観測区間におけるマルチパスの状態も不連続性に影響する。ヒトからの直接反射信号は前後の観測区間で比較的安定して受信される傾向にある一方、マルチパスによる反射信号は、ヒトや周囲環境の状態に応じて各観測区間で異なる伝播経路を取ることがある。直接反射信号とマルチパスによる反射信号は、互いに干渉することで受信強度の変動や波形の歪みを引き起こす。ビンによる選択基準は他の選択基準とは異なり、各観測区間で伝播経路が大きく異なる反射信号や、安定した受信強度が得られない反射信号を選択しづらくする働きがある。様々な伝播経路をとることで波形の歪みを増大させる、マルチパスによる反射信号の影響を抑制し、ヒトからの直接反射信号をもとに推定した波形が選択され易くなることで、不連続性の低減が期待できる。

図7は、表1と表2に示した結果において提案手法による不連続性指標値の低減効果が最も高かった被験者Aのリファレンス連続波形、選択基準なしとして構成した連続波形と各提案手法を用いて構成した連続波形を併せて示している。図中の破線は20 sごとの観測区間境界を表している。図8は、観測区間境界における不連続性低減の一例として、図7の160 s時点と560 s時点付近の波形を拡大して示したものである。同図から、選択基準なしの場合に見られる不連続性が、いずれの提案手法を用いた場合でも同程度に低減され、リファレンス波形に近い波形が得られていることがわかる。

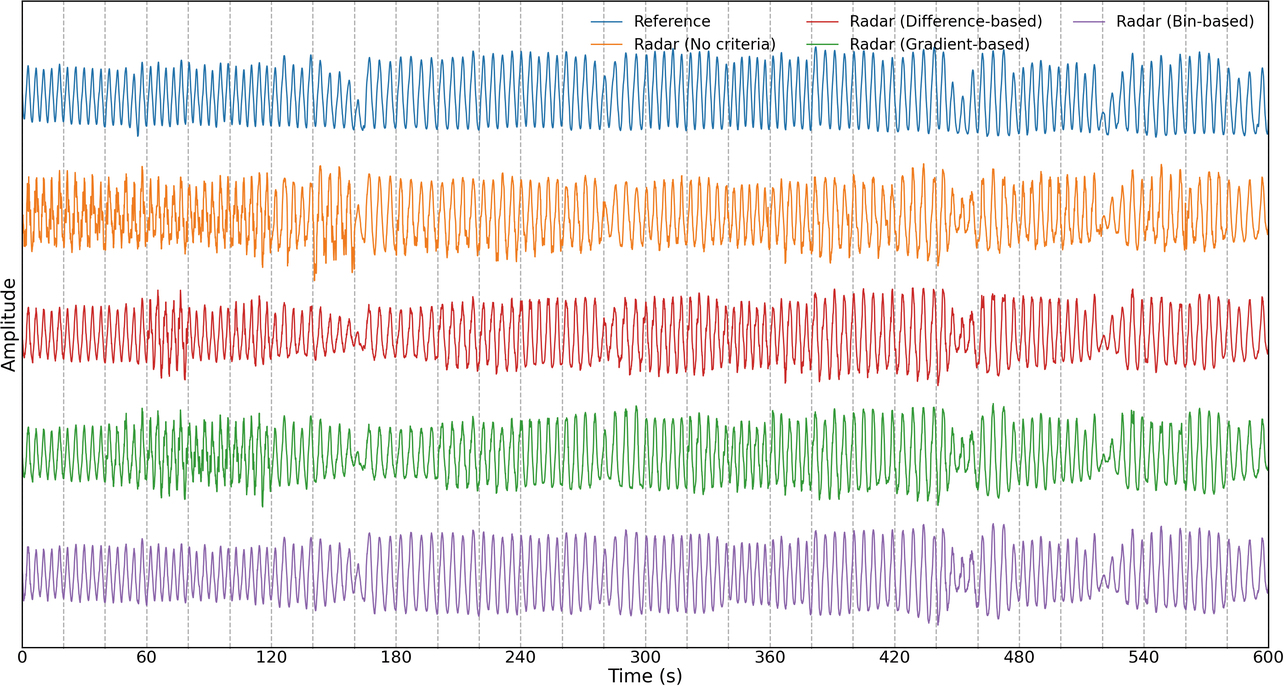
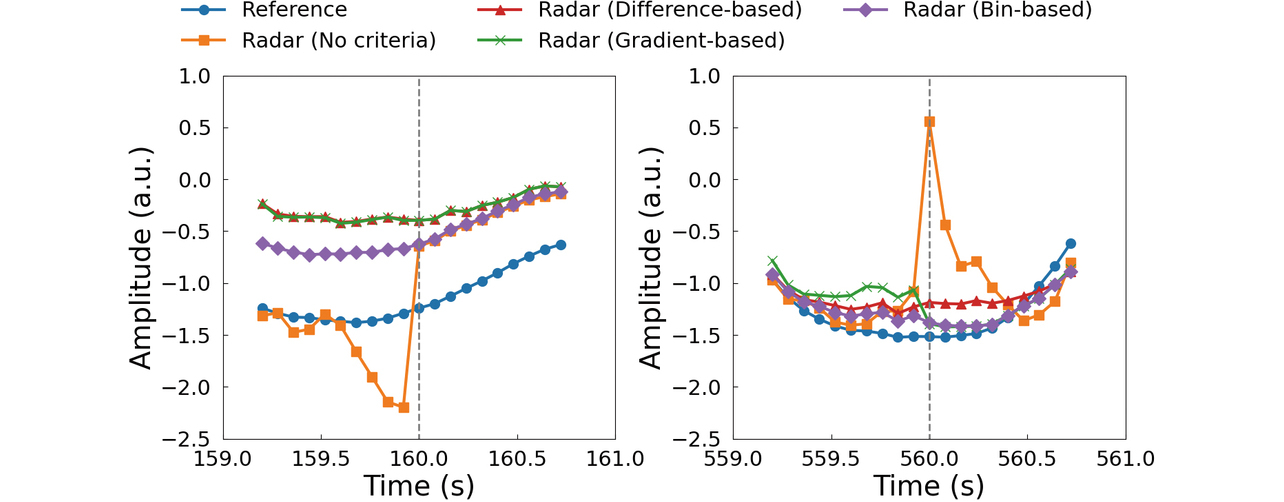
また、図7の選択基準なしとして構成した波形において、特に0 sから160 sにかけて顕著に見られる波形の歪みが、同図の提案手法を用いて構成した波形では明らかに低減されていることがわかる。ここに、表2で示した観測区間境界以外での不連続性指標値の低減効果が表れている。差・傾きによる選択基準を用いる手法では観測区間境界付近の変位推定値を判断基準としているが、前述したように観測区間境界以外においても、ある程度の波形不連続性の低減効果がある。さらにビンによる選択基準を用いて構成した波形に注目すると、他の選択基準を用いた場合の波形と比較して歪みがさらに低減され、しかも各観測区間における波形振幅の変化傾向がリファレンス波形に近づいていることがわかる。これは、歪みが少なく、安定した波形を得やすいビンによる選択基準の効果を反映していると考えられる。以上のことから、限られた被験者数ではあるものの、三つの提案手法にはいずれも波形不連続性の低減効果があり、中でもビンによる選択基準を用いる手法が最も高い効果を示す傾向にあることを確認した。

6. むすび

本論文では、レーダにおけるヒトの呼吸波形計測を対象として、所定周期で繰り返される観測区間で推定した波形群をもとに不連続性の小さい連続波形を構成するための波形選択手法を提案した。提案手法の有効性を評価するための不連続性指標を導入し、シミュレーションによって指標が機能することを示した。ミリ波レーダを用いた複数人の呼吸波形計測実験において提案手法を適用し、限られた被験者数ではあるものの、指標を用いた評価で各被験者の連続波形に含まれる不連続性が低減することを示して提案手法の有効性を明らかにした。

今回得られた結果は、限られた数の被験者を対象にしたものに留まるため、より多くの被験者に対して提案手法の有効性を明らかにすることが必要である。また、提案手法は本来の呼吸波形には不連続性が含まれないことを前提にしているが、呼吸の状態に異常が生じた場合、波形として選択されないような不連続性が含まれることも想定される。そのため、連続波形をもとにヒトの状態を推定する実際のアプリケーションにおいて、提案手法が推定結果に与える影響を検証していくことも必要である。

今後、これらの課題も踏まえ、レーダを用いたバイタルサイン計測の展開を検討していく。

参考文献

1）

Y. S. Can, B. Arnrich, and C. Ersoy, “Stress detection in daily life scenarios using smart phones and wearable sensors: A survey,” J. Biomed. Inform., vol. 92, 2019, 103139.

2）

A. L. Alfeo, P. Barsocchi, M. G. C. A. Cimino, D. L. Rosa, F. Palumbo, and G. Vaglini, “Sleep behavior assessment via smartwatch and stigmergic receptive fields,” Pers. Ubiquitous Comput., vol. 22, no. 2, pp. 227-243, 2018.

3）

日向匡史, 木下航一, 西行健太, 長谷川友紀, “自動運転時代におけるドライバモニタリング技術,” OMRON TECHNICS, vol. 50, no. 1, pp. 36-31, 2018.

4）

J. Yin, D. Zhu, M. Shi, and Z. Wang, “Depth Maps Restoration for Human Using RealSense,” IEEE Access, vol. 7, pp. 112544-112553, 2019.

5）

G. Paterniani et al., “Radar-Based Monitoring of Vital Signs: A Tutorial Overview,” Proc. IEEE, vol. 111, no. 3, pp. 277-317, 2023.

6）

M. Alizadeh, G. Shaker, J. C. M. D. Almeida, P. P. Morita, and S. Safavi-Naeini, “Remote Monitoring of Human Vital Signs Using mm-Wave FMCW Radar,” IEEE Access, vol. 7, pp. 54958-54968, 2019.

7）

T. Koda, T. Sakamoto, S. Okumura, and H. Taki, “Noncontact Respiratory Measurement for Multiple People at Arbitrary Locations Using Array Radar and Respiratory-Space Clustering,” IEEE Access, vol. 9, pp. 106895-106906, 2021.

8）

T. Penzel et al., “Cardiovascular and respiratory dynamics during normal and pathological sleep,” Chaos, vol. 17, no. 1, 2007, 015116.

9）

H. D. Cohen, D. R. Goodenough, H. A. Witkin, P. Oltman, H. Gould, and E. Shulman, “The Effects of Stress on Components of the Respiration Cycle,” Psychophysiology, vol. 12, no. 4, pp. 377-380, 1975.

10）

阪本卓也, ワイヤレス人体センシング, オーム社, 2023.

11）

A. Albanese, L. Cheng, M. Ursino, and N. W. Chbat, “An integrated mathematical model of the human cardiopulmonary system: model development,” Am. J. Physiol. Heart Circ. Physiol., vol. 310, no. 7, pp. H899-H921, 2016.

12）

B.-K. Park, O. Boric-Lubecke, and V. M. Lubecke, “Arctangent demodulation with DC offset compensation in quadrature Doppler radar receiver systems,” IEEE Trans. Microw. Theory Tech., vol. 55, no. 5, pp. 1073-1079, 2007.

13）

Q. Lv, D. Ye, S. Qiao, Y. Salamin, J. Huangfu, and C. Li, “High dynamic-range motion imaging based on linearized Doppler radar sensor,” IEEE Trans. Microw. Theory Tech., vol. 62, no. 9, pp. 1837-1846, 2014.

14）

山田寛喜, “ミリ波レーダによる高分解能イメージング技術,” 電子情報通信学会論文誌 B, vol. J104-B, no. 2, pp. 66-82, 2021.

15）

松浦圭記, 川上莉穂, 谷本雄大, 齋藤啓介, “ミリ波レーダを用いた時系列クラスタリングによる複数人の呼吸数計測の実現,” OMRON TECHNICS, vol. 56, no. 1, pp. 97-104, 2024.