低接触抵抗と高容量開閉を両立するリレー開閉機構の開発
- 低接触抵抗
- 高容量開閉
- 集中抵抗
- 開閉機構
- 衝撃力
近年、環境問題への対策として利用が高まっている太陽光発電などに代表される再生可能エネルギーにおいてシステムの高効率化とメンテナンスフリー化が推進されている。高効率化のためにシステムの高電圧化が加速しており、また大電流通電時の発熱における種々の不具合抑制のため、系統連系部に使用されるリレーについても大電流通電時の発熱抑制および高電圧大電流の高容量開閉を両立するリレーが求められている。
本検討では、はじめに低接触抵抗を実現する接点材料・機構の選定を行った。次に、高容量開閉時に発生する接点溶着の引きはがしに適した構造およびその構造での引きはがし力の導出方法を検討した。高容量開閉を可能にするため、従来の設計で使用していた接点接触力や接点押込み量などに加え、引きはがす瞬間における運動量変化を、新たな設計パラメータとした。今回の検討により、低接触抵抗と高容量開閉を両立する開閉機構の技術を確立した。
1. まえがき
地球温暖化などの環境問題に対する意識の高まりから、太陽光発電等を用いた再生可能エネルギー市場が拡大している。太陽光で発電された直流電圧を、商用および家庭用で使える交流電圧に変換するための太陽光発電用インバータ(以下、PVインバータ)において、系統連系部にリレーが使用される。
系統連系部に使用されるリレーは、システムの安全用途として朝晩における定期的な開閉および緊急時の遮断に用いられ、また最大発電時には大電流の通電も必要となる。大電流通電時において、リレー接点ON時に生じる接触抵抗が大きい場合には発熱が大きくなり、PVインバータへの悪影響がある。そのため従来の家電・産業機械向けなどの汎用リレーと比較し低接触抵抗が求められる。今回の検討ではこの発熱課題を解決するため、初期接触抵抗0.2mΩ以下という業界トップラスの低接触抵抗を目標値とした。
ただし低接触抵抗を実現するためには導電率の良い接点材を使用する必要があり、そのような材料では電気的な開閉時に、アーク放電による接点溶融が起こりやすく、接点ON状態で止まってしまう溶着故障が発生する可能性が高まる。
また、PVインバータの高効率化のための高電圧化トレンドに伴い部品自体の高絶縁性能が求められる。このため回路の直接的な遮断機能を担うリレーにおいては、限られたスペースの中で空間絶縁距離を大きく取る必要がある。その方策としては、一対の接点によるシングルブレイク構造よりも、二対の接点を直列に配置するダブルブレイク構造の方が、大きな空間絶縁距離を取ることができるため望ましい。ただし、ダブルブレイク構造では接触点が増えるため接触抵抗が増大する問題がある。
従来技術では、高容量遮断のためには添加剤入りの接点を使用しており、接触抵抗低減のためには大きな接点接触力が必要であった。一方で、添加剤入りの接点は接触抵抗のばらつきが大きく、異常発熱のリスクがある。また接点接触力の増大に伴いリレーの駆動コイルが大型化し、全体サイズが拡大する問題がある。
そこで我々は低接触抵抗と高容量開閉を両立するリレーを以下の構成で実現した。
- 低い通電抵抗の実現のため純Ag系接点を使用
- 接触抵抗低減のためリレー内部の通電路を並列化
- 高電圧を安全に遮断するためダブルブレイク構造を採用
- 電気的開閉時の溶着事象を開離する構造仕様を運動量変化による力積で設定
また本稿では以下の構成で述べる。
第2章では低接触抵抗を実現するための理論式の構築、接点材質の選定、および実測値の比較評価から実現可能な構造を導いた結果を述べる。
第3章では溶着事象を引きはがす機構の選定、および設計仕様として開離機構の運動量変化から計算される力積に着目した検討結果を述べる。
第4章では第2、3章の検討結果に基づく開閉機構における力積の設計パラメータ検討結果を述べる。
第5章では本検討結果の振り返りと残課題及び今後の展望について述べる。
2. 低接触抵抗を実現する材料と構造の検討
2.1 初期接触抵抗の理論式構築
リレーの接点材質は、純Ag系接点と添加材入りAg接点に大別される。更に添加材入りAg接点はAg+金属(Me)およびAg+金属酸化物(MeOx)のものが一般的である。一般的に接触抵抗は純Ag系接点<Ag+Me<Ag+MeOxであるが、耐溶着性は逆の傾向となる。従来の負荷開閉に利用されるリレーは、アークによる溶着に対して強い金属酸化物(MeOx)の添加材入り接点材質を選定することで開閉性能を向上させつつ、接触抵抗については数十mΩまで許容されていた。PVインバータ向けリレーでは開閉性能と共に1mΩ以下の低接触抵抗も求められる。本検討では、目標とした初期接触抵抗0.2mΩ以下を実現するため、Ag+MeOxの接点材質は適さないと判断し、抵抗率の低いAg含有量99%以上の純Ag系接点:接点材質A、および従来の汎用リレーに使われているAg含有量90%程度のAg+Me接点接点材質Bの二種類に絞り込み、理論式と実現可能な構造を検討した。
リレーの接触抵抗は、導電部の導体抵抗、接触部の集中抵抗、接触面の境界抵抗の3つに分類される。導体抵抗は導体部の材料の導電率と部品形状により算出でき、固定値となる。本章では、集中抵抗と境界抵抗の和の低減を検討の対象とした。そのため集中抵抗理論式から理想の接触抵抗を想定した上で、実測値における集中抵抗値+境界抵抗値を理論値に近づけるパラメータ値及び構造検討を行った。
接点接触部の集中抵抗の理論としては、ホルムの近似式が知られている1,2)。

- Rk
- :集中抵抗[Ω]
- ρ
- :抵抗率 [Ω.m]
- r
- :接触半径[m]

- P
- :接触力 [N]
- E
- :縦弾性係数[MPa]
- ν
- :ポアソン比[-]
- R
- :曲率半径 [m]
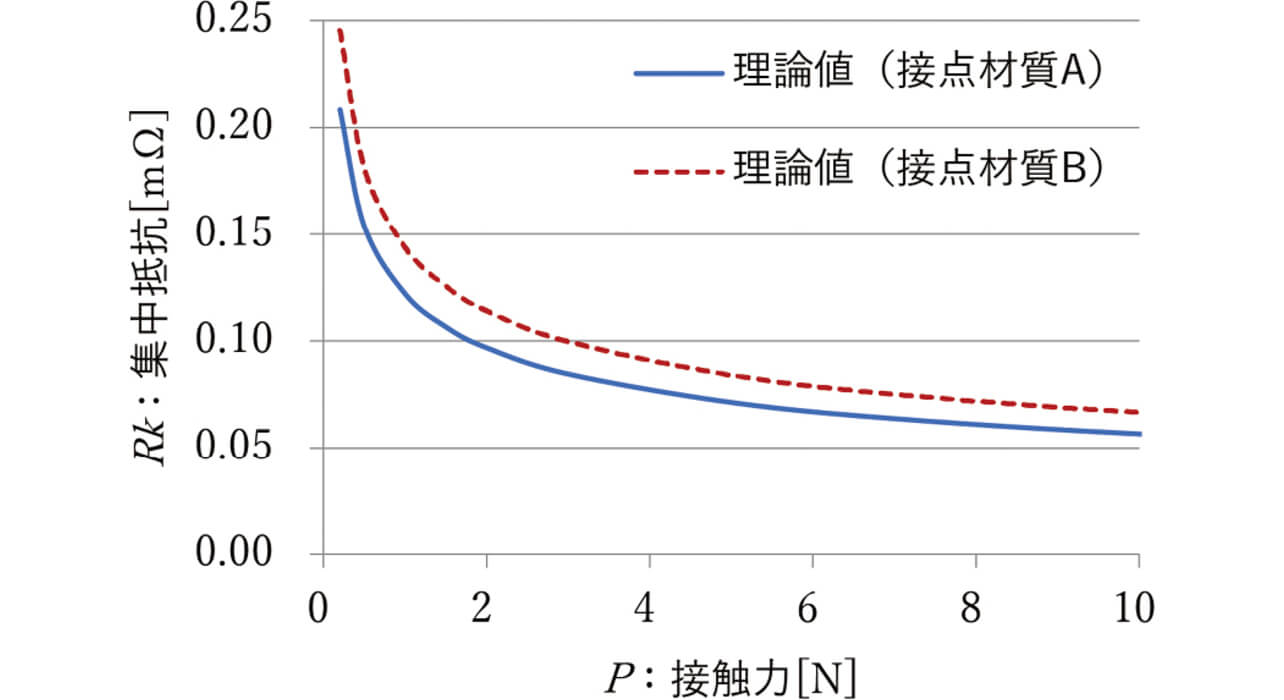
式(1)、(2)に示した理論式において、接点材質AおよびBを用いて、接触力を変化させた時の集中抵抗の計算結果を図1に示す。また計算に使用した数値を表1に示す。
| 接点材質A | 接点材質B | ||
|---|---|---|---|
| 抵抗率[Ω] | 1.63×10-8 | 1.92×10-8 | |
| 縦弾性係数[MPa] | 90000 | ||
| ポアソン比[-] | 0.33 | ||
| 曲率半径[m] | 可動接点 | 0.020 | |
| 固定接点 | 平面(∞) | ||
理論計算では、抵抗率の比15%がそのまま集中抵抗の違いとして表れた。
2.2 初期接触抵抗の実測結果
図2に示すプランジャ型リレー構造を用い、接点材質A、Bを接触力2N近傍で実測した比較を表2に示す。抵抗値は電圧降下法により測定した3)。実測においては導体抵抗も含まれているため、算出した導体抵抗を実測した値から除外した。また測定した構造において接点の接触部が二か所あるため、両接点の平均値を実測値とした。
| 接点材質 | |||
|---|---|---|---|
| A(n=7) | B(n=4) | B/A | |
| 理論値[mΩ] (P :2N近傍) |
0.091~0.095 | 0.110~0.117 | 118% |
| 実測値[mΩ] (平均値) |
0.098~0.123 (0.111) |
0.156~0.170 (0.166) |
(149%) |
| 実測値/理論値 (平均値) |
107%~132% (119%) |
142%~153% (147%) |
|
表2より以下のことが確認できた。
- 1)
- 理論値ではAとBの差は18%だが、実測値では平均値の比較で49%の差がある。この差異は、実測値の材料硬度のばらつきなどによる実接触部面積の違いや表面被膜などの影響を含んでいるためと推定した。
- 2)
- 接点材質Aは実測値/理論値が119%に対し、接点材質Bでは147%であり、理論値との差を生む要因の影響が大きい。
1)、2)より、低接触抵抗を安定して実現する目的から、これ以降は理論値と実測値の差異検討を接点材質Aに絞って実施した。
ここで、図2のプランジャ型リレーを用いて接点材質Aの接触力を変化させた時の接触抵抗値を実測した結果を図3に示す。ここで実線は集中抵抗の理論計算結果を表す。
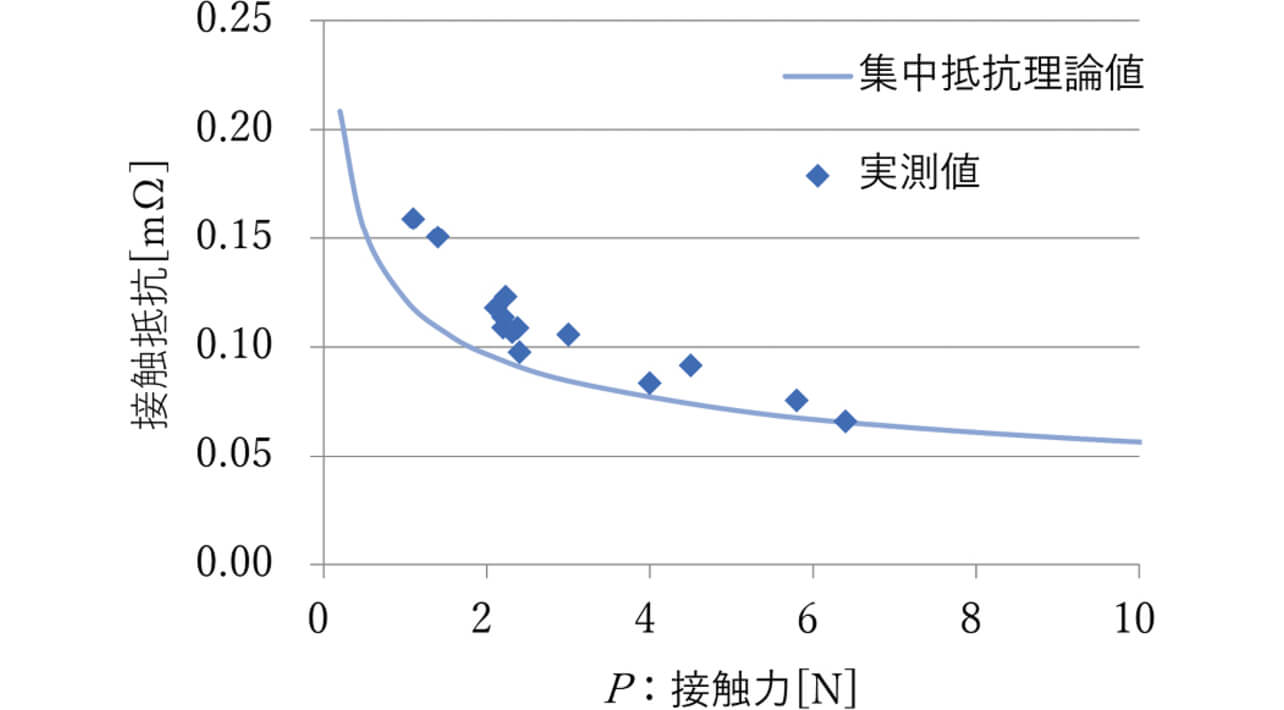
接触力が低い領域では接触抵抗は理論値から上方にばらついているが、接触力が上がるにつれ理論値と概ね合致した。ここで接触力に対して接触抵抗の実測値/理論値の比率を図4に示す。
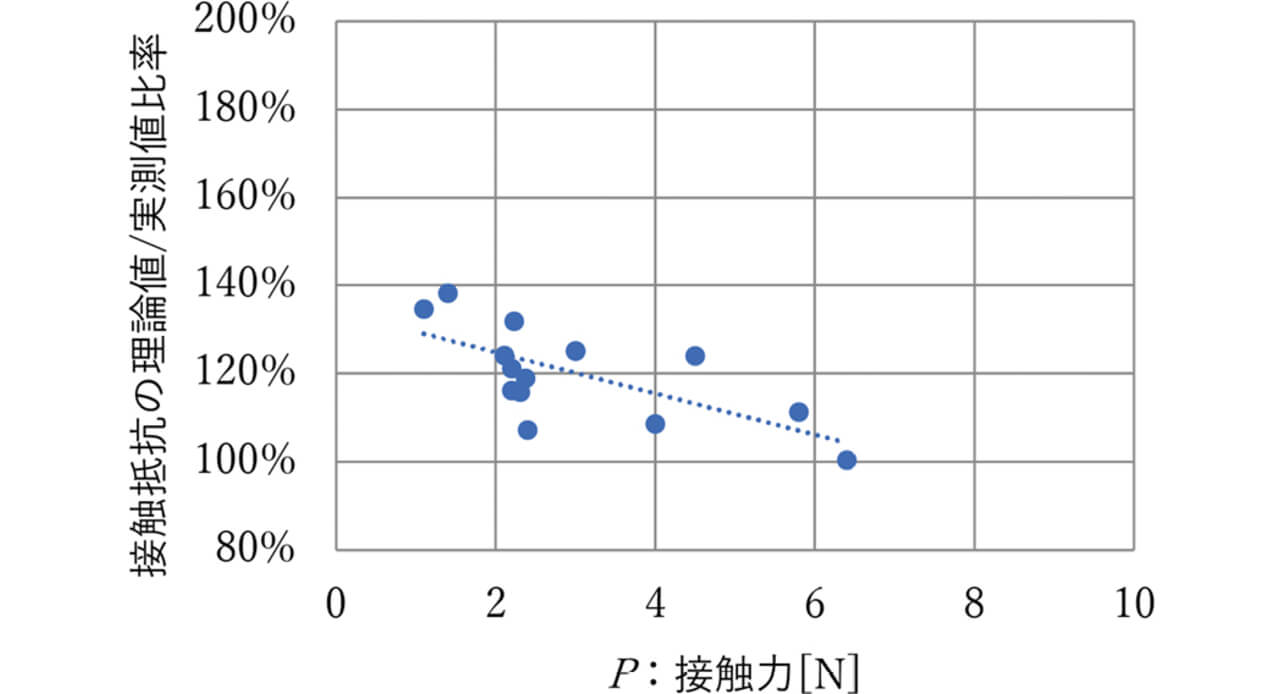
純Ag系接点では1N程度の接触力で表面粗さの違いによる接触抵抗への影響は小さくなることが知られている4)。本検討でも接触力が高くなると実測値が理論値に近づいていくことより、理論式との差異の要因として推定した接触面積や表面皮膜の影響について、接触力を適切な設計値とすることで低減できることが確認できた。この実測値と理論値との差異を考慮し構造検討を実施する。
2.3 低接触抵抗を実現する構造の検討
第1章でも述べたように高容量のPVインバータにおいては高電圧仕様になるため、リレーの開閉構造はダブルブレイク構造を採用する。その場合、接点が二対あるため接点部の接触抵抗が二か所で発生する。導体抵抗を0.05mΩと仮定すると、目標の0.2mΩの達成には集中抵抗と境界抵抗を合わせた値を0.15mΩ以下に抑えなければならず、ダブルブレイク構造では一対の接点当たり0.075mΩに抑える必要がある。この時一対の接点に必要な接触力は、図3に示す集中抵抗理論値において約4Nであり、両側接触力で8N必要となる。この接触力を発生させるためには駆動力が大きくなってしまい、コイルブロックが大型化し、リレーの小型化に影響が出る。
この課題を解決するため、同じ接触力でも接触抵抗が小さくなるよう、通電路となる可動端子が一つのシングル接点構造から、二つの可動端子を並列化するツイン接点構造を検討する。同じ駆動力において一つ一つの接点にかかる接触力は分散するため一か所の接点での接触抵抗は大きくなるが、図5のように並列化により全体の接触抵抗は小さくすることができる。
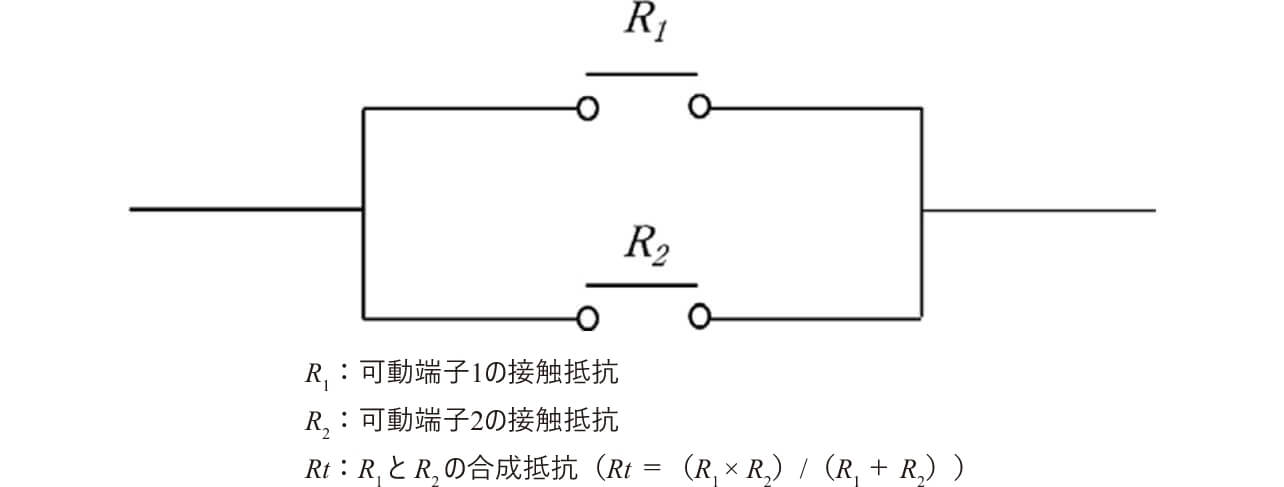
各接点にかかる接触力の和をPtotal とし、Ptotal とダブルブレイク構造でのシングル接点構造およびツイン接点構造での集中抵抗の理論値を図6に示す。
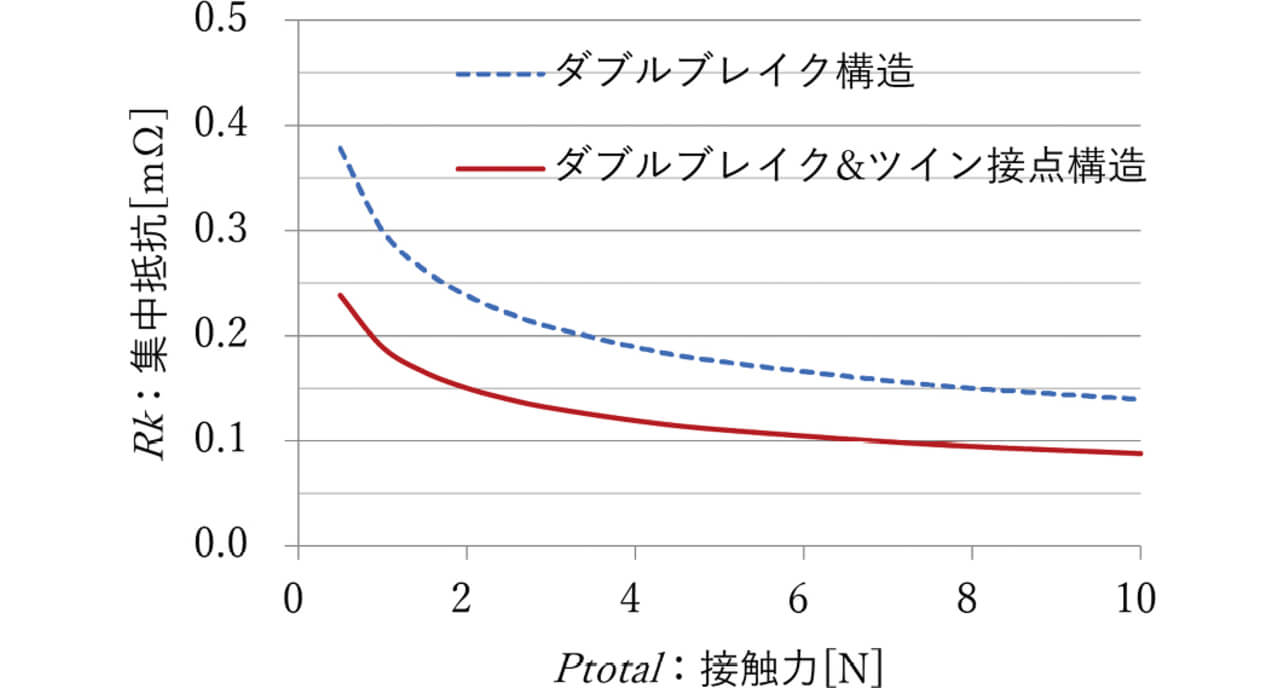
先述の内容と同様に導体抵抗を0.05mΩと仮定した時、許容可能な集中抵抗は0.15mΩであり、シングル接点構造では理論値でもPtotal は8N必要だったのに対し、ツイン接点構造ではPtotal が2Nで達成できることがわかる。またツイン接点構造では、各接触力がばらつき接触抵抗差がある場合でも合成抵抗差は小さくなり、接触抵抗を安定化させることがシングル接点構造に比べ容易なため、ダブルブレイク& ツイン接点構造を採用する。
3. 高容量開閉における開閉機構の運動量変化による溶着引きはがしの検討
3.1 純Ag系接点を用いた高容量開閉構造
低接触抵抗を実現するために、純Ag系接点を用い、かつダブルブレイク& ツイン接点構造を定めた。
ここで、リレーは電気的な開閉を行うことが必須機能であるが、純Ag系接点においては電気的開閉時の接点バウンスによる断続的な電流遮断時に発生するアーク放電により溶着故障を起こしやすい問題がある。
溶着故障を回避するためには、そもそも溶着が発生しないようにするか、溶着しても引きはがしできればよい。溶着が発生しないようにするには接点接触時のバウンスをなくすことで達成されるが、機械的挙動によるリレーにおいてそのような動きを簡単な機構で実現するのは困難である。そこでまずは単純なダブルブレイク構造で開閉機構の検討を行った。
3.2 運動量変化で計算される力積に着目した溶着引きはがしの検討
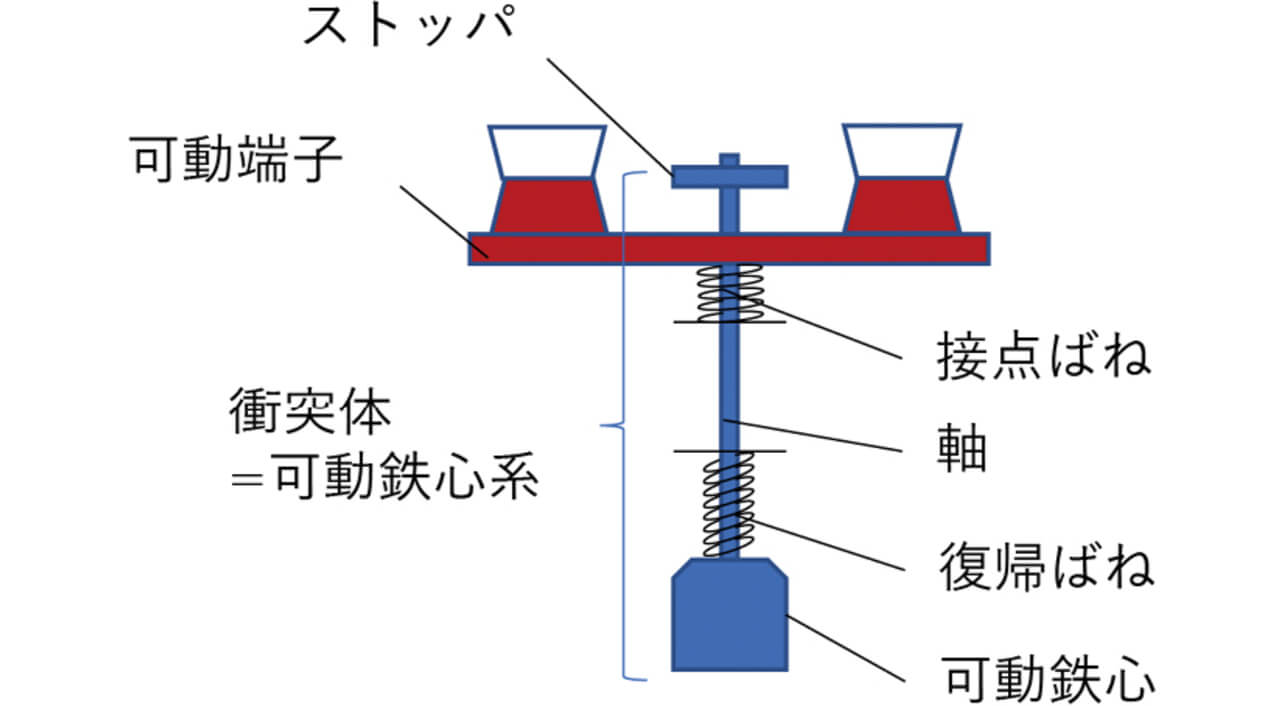
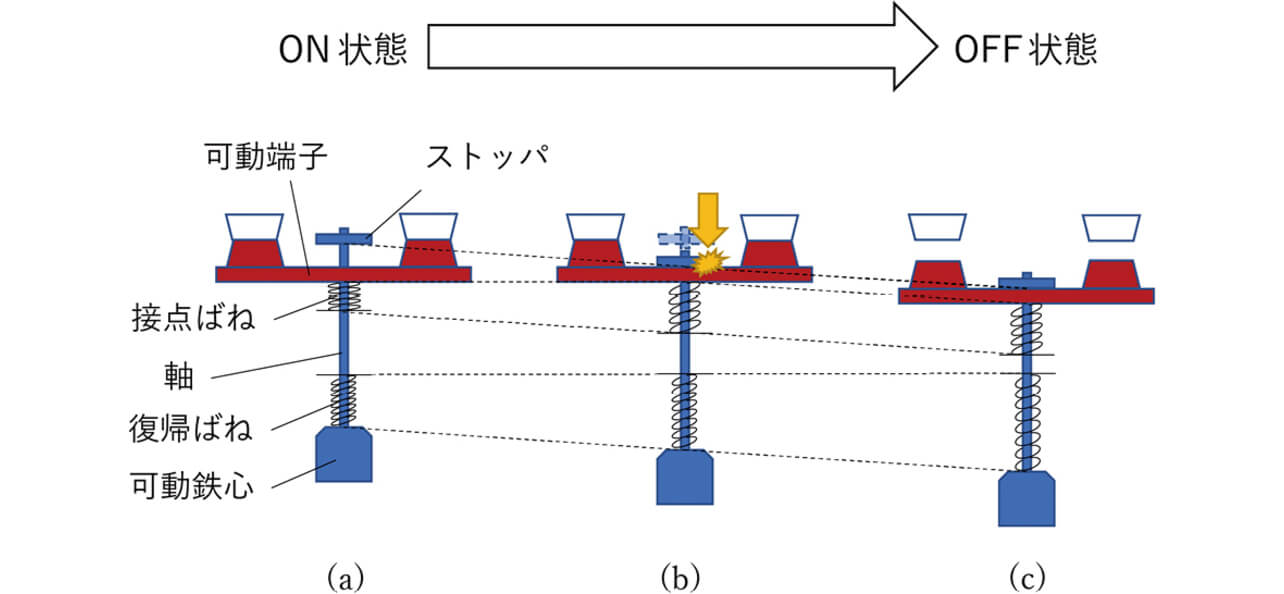
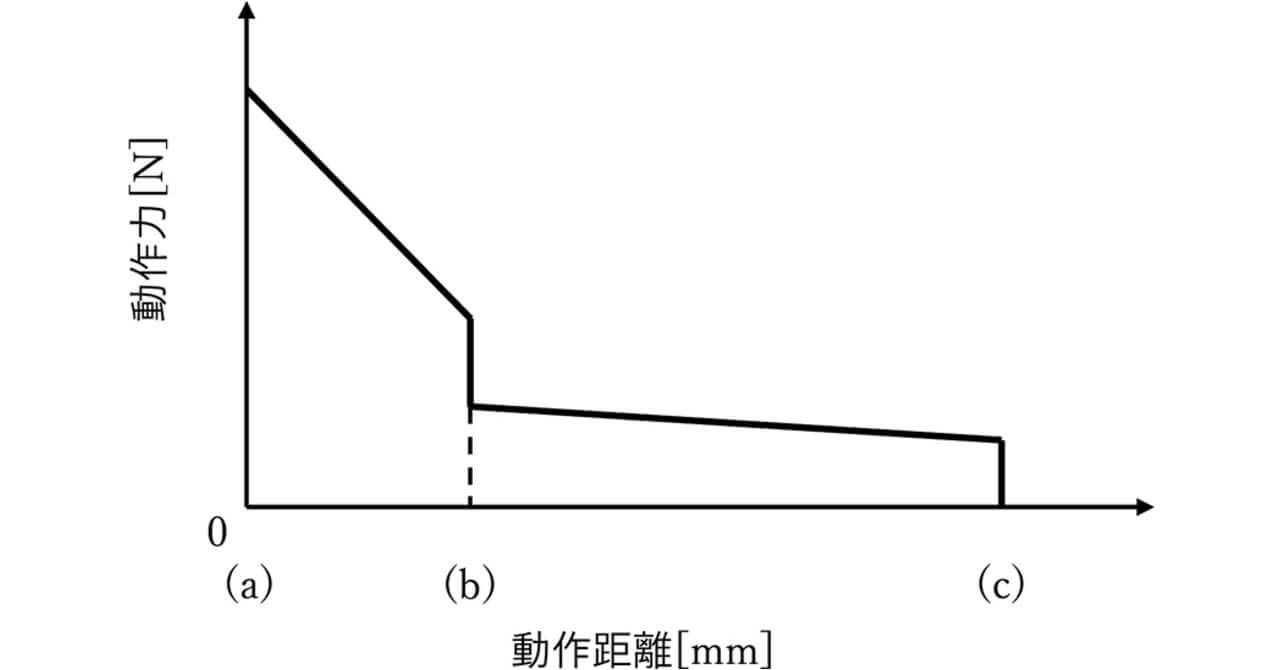
PVインバータ用途の一般的なリレーの開閉構造を図7に示す。本構造ではばねによる接点の開離時の運動のみで溶着を引きはがしており、引きはがし力を上げるにはばね定数を上げるか接点の押し込み量を大きくする必要があり、リレーが大型化する問題がある。一方、図8に示したプランジャ型リレー構造では、図9のように遮断時に可動鉄心と軸を介して接続されているストッパが可動端子に衝突するタイミングで、大きな衝撃力が発生する。この衝撃力により強い溶着を引きはがすことを期待できる。図9において、(a)は接点が完全に押し込まれた状態、(b)はON状態からOFF状態に遷移する時に接点が開離する(ストッパが可動端子に衝突する)瞬間、(c)は完全にOFFになった状態である。この(a)~(c)に至る遷移を、横軸に衝突体の動作距離、縦軸に衝突体の動作力(可動鉄心系を押し込んだ時の接点ばねおよび復帰ばねによる力)として図10に示す。なお、衝突体は可動鉄心および軸、ストッパを含めた可動鉄心系全体で構成される。この衝撃力は衝突体の運動量変化によって発生するため、運動量変化で計算される力積に着目した引きはがし効果について検討を行った。
衝撃力F は衝突体の運動方程式より以下の式で計算できる5)。

- m
- :衝突体の質量 [kg]
- α
- :衝突体の加速度 [m/s2]
- ν
- :衝突体の衝突直前速度[m/s]
- ν’
- :衝突体の衝突後速度 [m/s]
式(3)にΔt をかけると、

となり、衝撃力F は運動量の変化量で表される力積I により代替可能である。
図11に示すように、衝突体の質量m は可動鉄心および軸、ストッパを含めた可動鉄心系全体の質量となる。
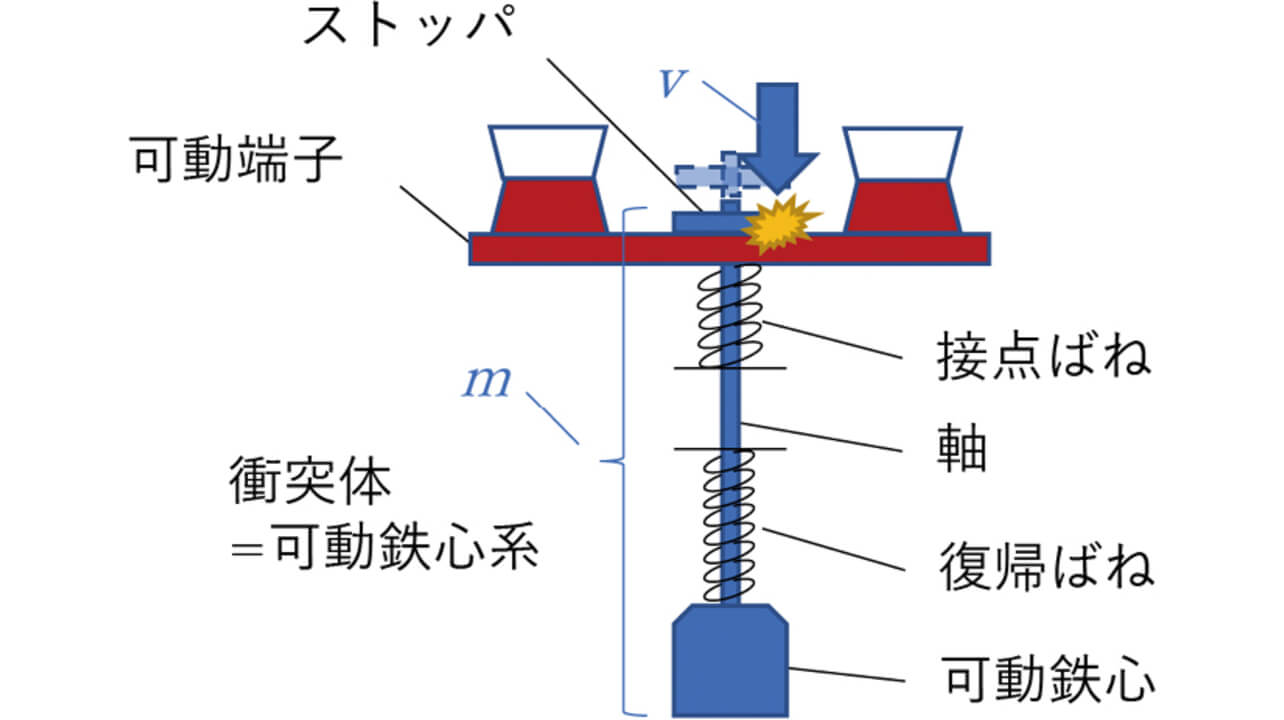
衝突体の速度導出のため高速度カメラによりストッパの変位を測定する。ストッパが可動端子に当たった瞬間をより正確に判別するため、接点が開離するタイミングをオシロスコープにて電気的に取得し、高速度カメラと同期させて測定した。
接点開離直前のストッパの速度を変位より算出し、接点開離のタイミング直前における速度をv とした。この測定例を図12に示す。ここで横軸は変位測定の時間、縦軸はストッパの変位および速度である。
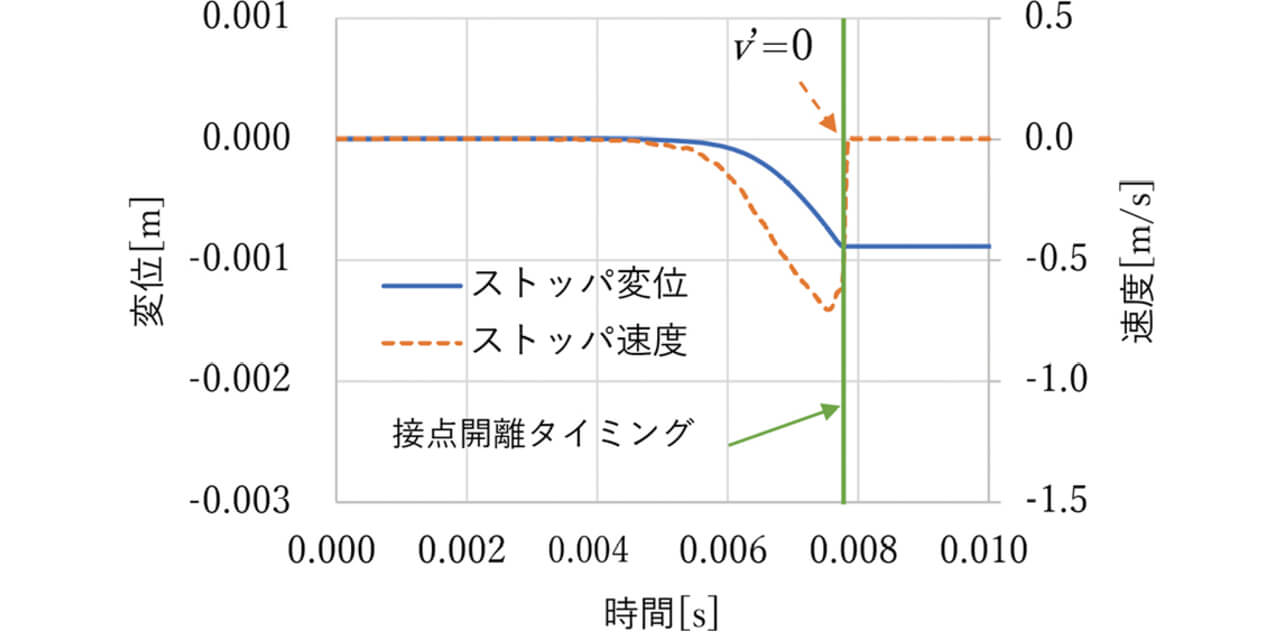
ここで接点が完全に溶着している状態を仮定し、ストッパが速度v で可動端子に当たり、速度v’=0になるとした場合の力積I を式(4)を用いて算出し、電気的開閉試験による目標回数内での溶着故障の有無の関係について確認したところ、図13のように力積I の大小で2分化された。ここで力積I は目標回数に達した中で最も小さいものを1として比率で示した。目標回数を達成するための力積I のしきい値が確認できた。
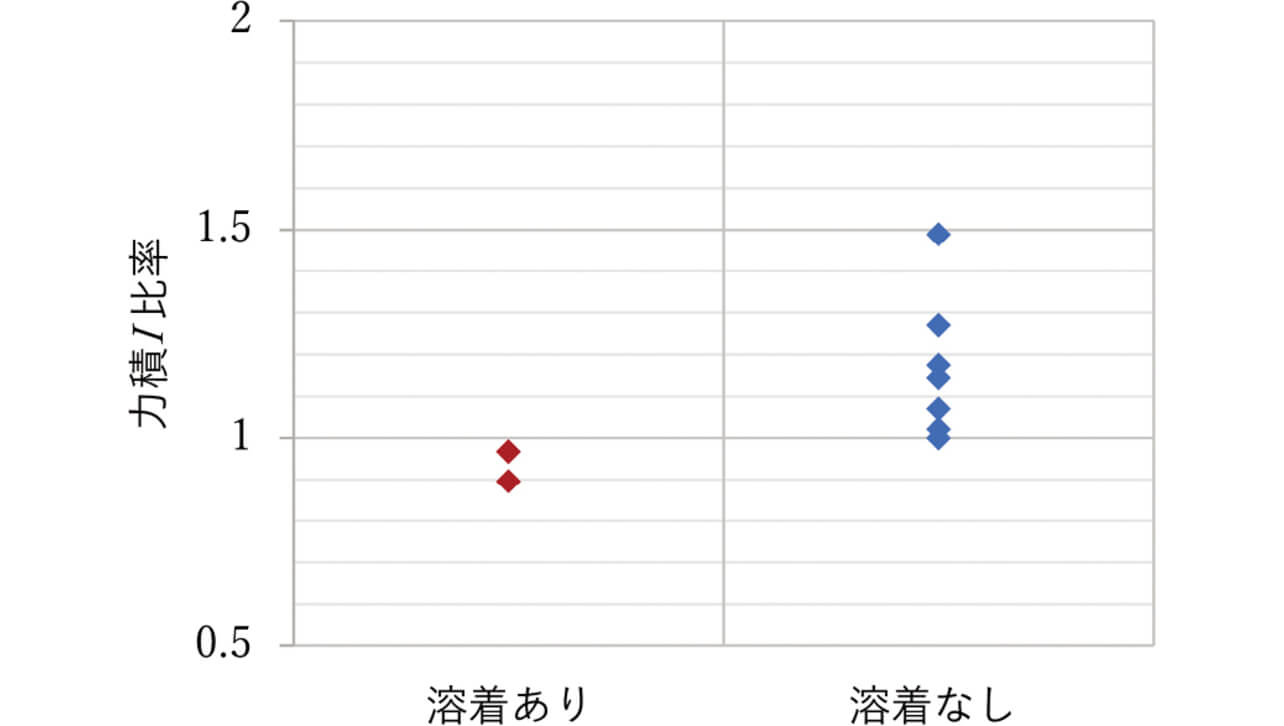
ここで力積I についてエネルギー保存の法則の観点より考察を行う。図8のようなプランジャ型リレーにおいて、(a)のリレーON状態では接点ばねおよび復帰ばねが圧縮されることで弾性エネルギーが蓄積されている。リレーON状態からOFF状態に遷移する時に弾性エネルギーが衝突体の運動エネルギーに変換されることでストッパが可動端子に衝突し、大きな運動量変化が発生する。ここでリレーがON状態から接点開離する瞬間までに消費されるばねの弾性エネルギーU [N・m] は、図10のリレー動作距離と動作力の関係より図14のハッチング部の面積で表される。
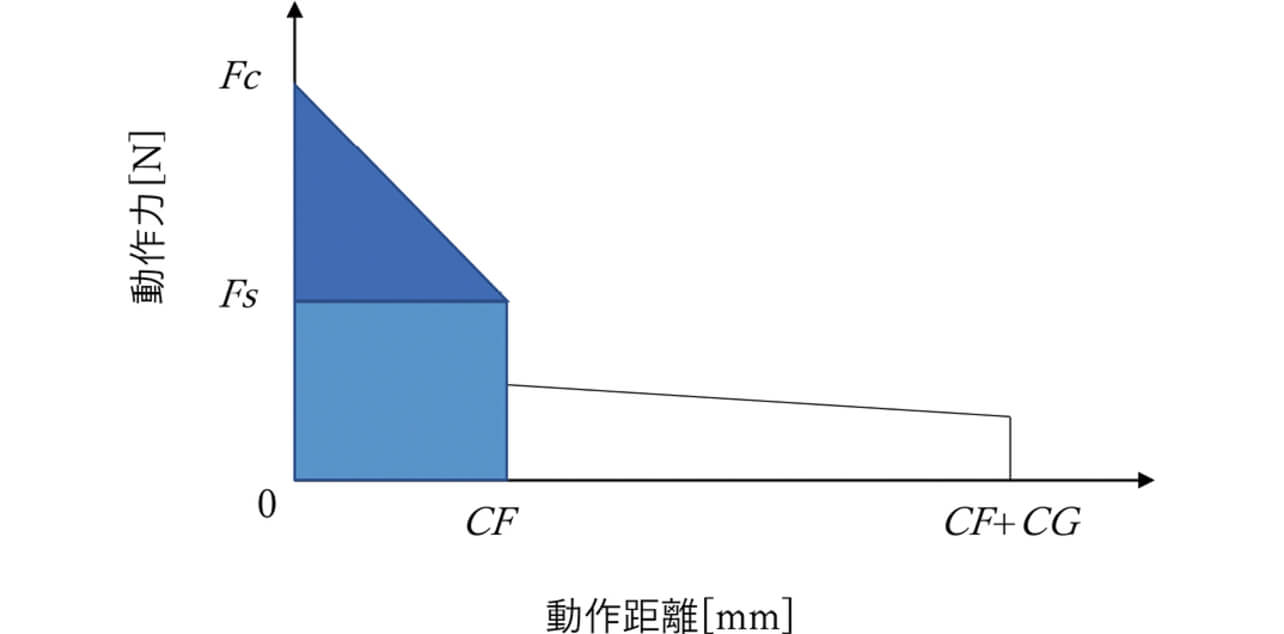

- Fc
- :ON状態の時の荷重[N]
- Fs
- :接点が開離する瞬間の荷重[N]
- CF
- :ON状態から接点が開離するまでの可動鉄心系の動作距離[mm]
- CG
- :接点が開離してからOFF状態になるまでの可動鉄心系の動作距離[mm]
ばねの弾性エネルギーU を横軸に、力積I を縦軸に取ったグラフを図15に示す。なお、ある基準サンプルにおけるFc 、Fs 、CF の値で式(5)を使用し算出したばねの弾性エネルギーU と、そのサンプルのストッパ速度を高速度カメラで測定し算出した力積I をそれぞれ1とし、比率で示す。
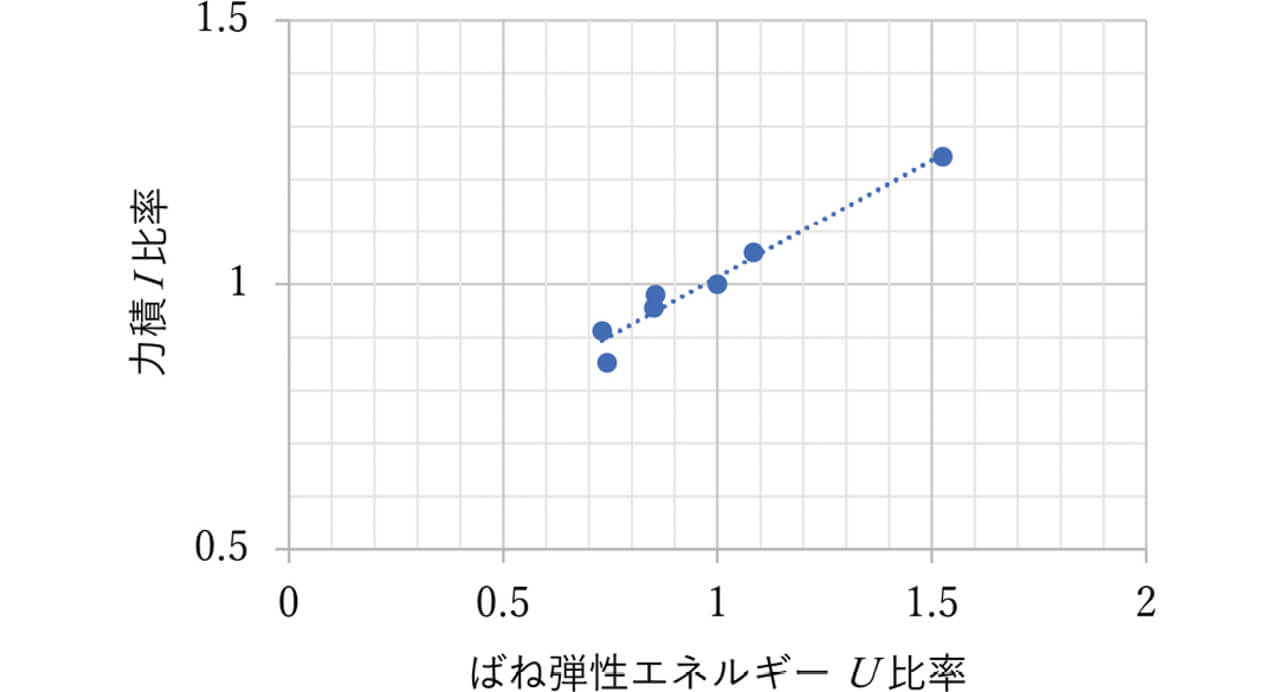
図15よりばねの弾性エネルギーU が力積I と線形の関係にあることがわかる。この結果より、機構の設計方法として、シャルピー衝撃試験などに代表される考え方と同様に、ばね弾性エネルギーで溶着部の引きはがし性能を設定できることを確認した。
4. ダブルブレイク&ツイン接点構造における溶着引きはがしの検討
これまでの検討結果より、低接触抵抗を実現しながら高容量開閉を行うために、図16に示すような、開閉部は図5と図8を合わせたダブルブレイク&ツイン接点構造とし、開閉機構はプランジャ型に定める。
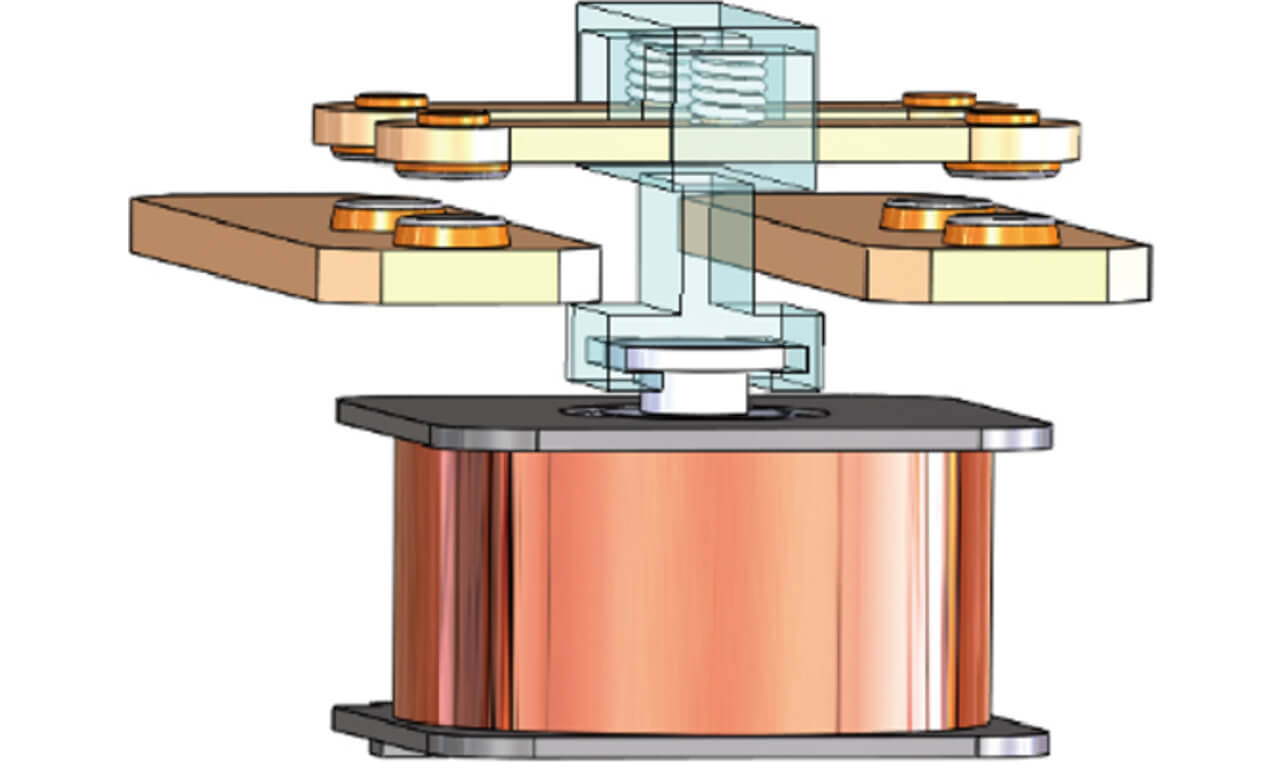
このダブルブレイク& ツイン接点構造かつプランジャ型機構における開閉性能についても、第3章で述べた従来のダブルブレイクのプランジャ型機構での引きはがし検討結果の考え方が問題なく設計活用できるか検討した。
ダブルブレイク& ツイン接点構造では独立した可動端子が二つあるため、ばねによるリレーの動作力と動作距離の関係は図17のようになる。
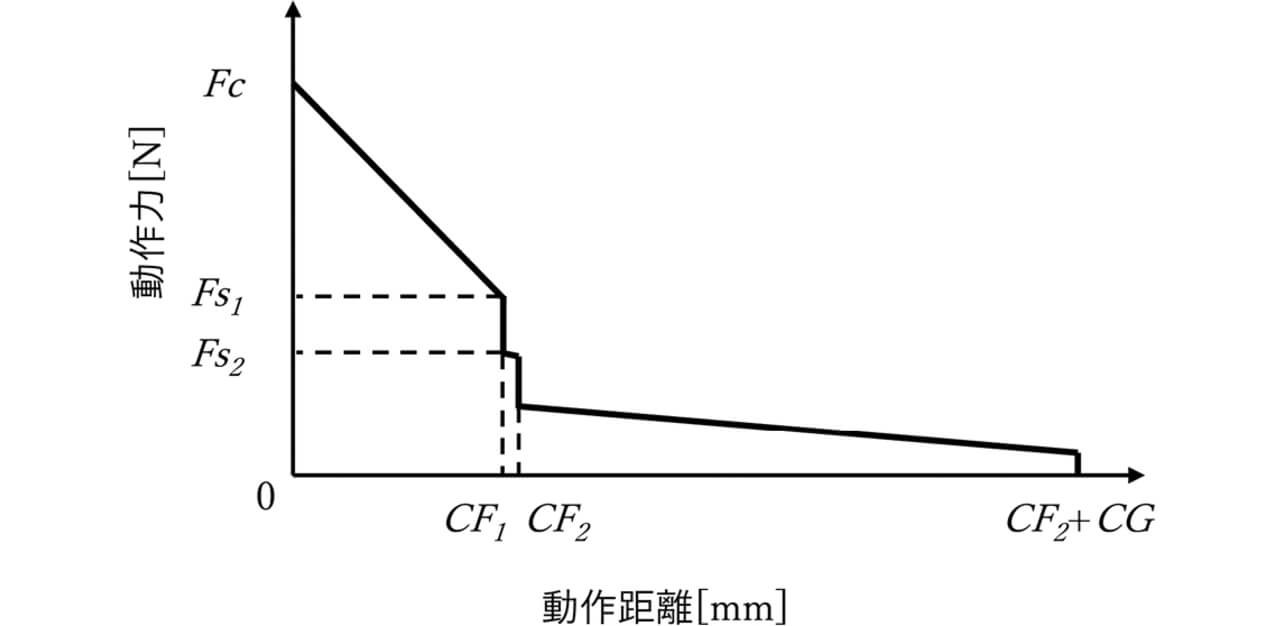
- Fc :
- ON状態の時の荷重[N]
- Fs1 :
- 可動端子1が開離する瞬間の荷重[N]
- Fs2 :
- 可動端子2が開離する瞬間の荷重[N]
- CF1 :
- ON状態から可動端子1(CFが小さい側)が開離するまでの可動鉄心系の動作距離[mm]
- CF2 :
- ON状態から可動端子2(CFが大きい側)が開離するまでの可動鉄心系の動作距離[mm]
- CG :
- 可動端子2が開離してからOFF状態になるまでの可動鉄心系の動作距離[mm]
ここで、二つの端子はそれぞれ開離するタイミングが異なるが、二つの端子のCF が小さい側をCF1と定義しており、開離のタイミングはCF1が早くなる。3.2項と同様にCF1側の端子およびCF2側のそれぞれの接点開離のタイミング直前における速度v1i 、v2i を高速度カメラにより測定し、力積を算出した。
二つの可動端子について、CF1のグラフを図18、CF2のグラフを図19に示す。ここで横軸はCFの設計最小値からのCF1もしくはCF2の実測値の比率、縦軸はそのCF に対応した可動端子に与えられる力積I について、3章で使用した数値で比率化したものである。またCF1とCF2の差を比差とし、その差を小・中・大と区別しプロットした。
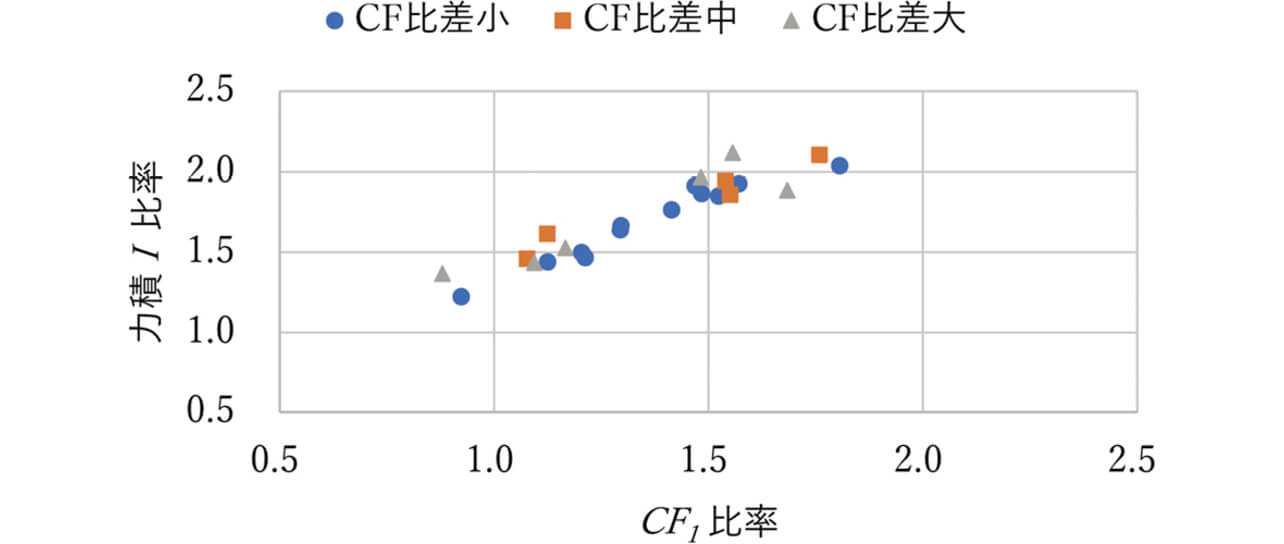
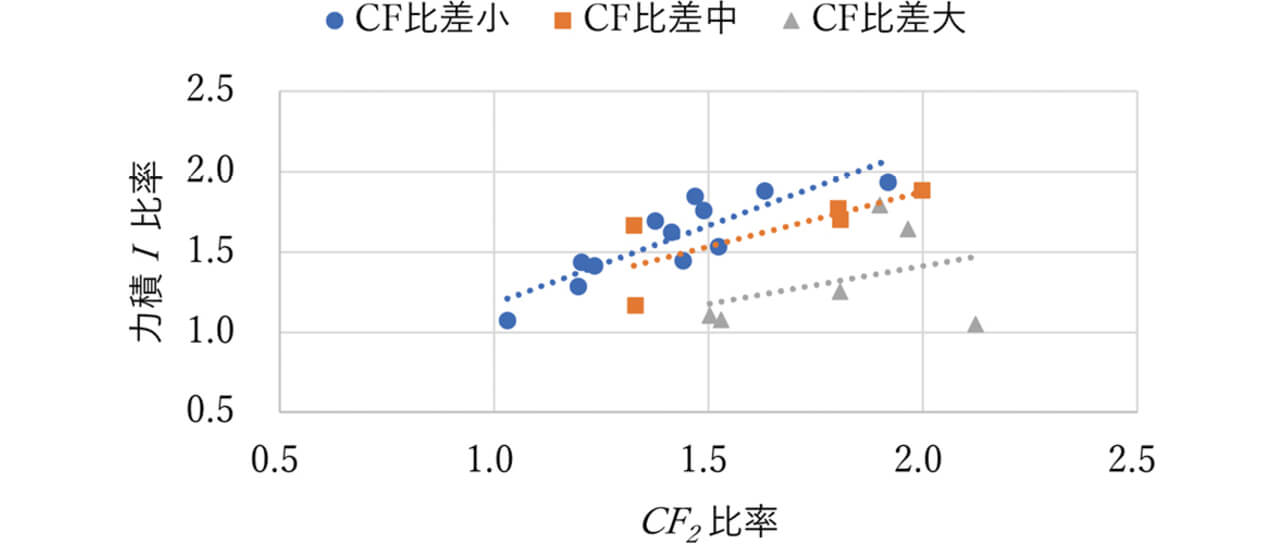
図18より、CF1と力積I との間にはCF 比差による影響は見られない。
一方で、図19よりCF2側の端子はCF 比差が大きい方が衝突体の力積が低下し、かつばらつきも増加する傾向にある。これは先に衝突するCF1側端子の衝突の影響をCF2側端子は受けるが、CF 比差が大きいほどCF1側端子衝突後からCF2側端子衝突までの衝撃体の速度が減少し、力積が増加しないためと考えられる。
これらの結果から、ダブルブレイク& ツイン接点かつプランジャ型機構を持つリレーにおいては、以下を確認できた。
- 3章で述べたばね弾性エネルギーに加えて、CF1とCF2の差も力積の設計パラメータとして重要である。
- 力積I が小さくなるCF2側を、3章の検討結果における力積I 比率が1以上となるように設計することで開閉性能が達成できる。
5. むすび
太陽光発電システムに用いられるPVインバータの大容量化と高効率化に伴い、使用されるリレーにおいても高電圧大電流の高容量開閉および大電流通電時の発熱抑制を両立していく必要がある。発熱抑制のために純Ag系接点を使用し、リレー内部の通電路を並列化することで低接触抵抗を実現した。さらに、純Ag系接点での電気的開閉時の溶着事象を、運動量変化で計算される力積で設計可能な衝撃により引きはがす機構の妥当性を、実験から検証できた。これらの検討結果を用いた開閉機構により、高容量パワーリレー群の中でも低接触抵抗と高容量開閉を両立するPVインバータ向けリレーとして、形G9KAを実用化した。
実使用条件においてはコイル駆動部の逆起電圧防止用のダイオードの有無や種類、リレー自体の取り付け方向性により開閉機構は影響を受けるが、今回の検討方法でしきい値を決定することで、それらを考慮した設計が可能となる。
今後はプランジャ型以外のリレーも考慮し、様々な溶着状態での複雑な開閉挙動における引きはがし力の算出に取り組み、再生可能エネルギーのより一層の普及に向け、安全かつ安定して通電・遮断のできるリレー商品開発を引き続き行う。
参考文献
- 1)
- 真野国夫.接触部品の信頼性,3版,総合電子出版社,1981, P303, 3055-20133-2213.
- 2)
- 澤田滋,清水佳織,島田茂樹,服部康弘.錫及び銀めっき電気接点の接触抵抗予測.SEIテクニカルレビュー.2010, No.177,7月号,p.36-42.
- 3)
- 愛知久史,松村年郎,宮地巌.銀、銅およびアルミ点接触子の直流300A通電時における接触抵抗特性.電気学会論文.1998, Vol. 118, No.7-8, p.825-830.
- 4)
- 浅井聡,関川純哉.銀接点対を用いた場合の接触抵抗―荷重特性の測定.[継電器・コンタクトテクノロジ]研究会.2017, No.203-2.
- 5)
- 小出昭一郎.物理学.35版,裳華房,1990, p.378, 4-7853-2019-2.
本文に掲載の商品の名称は、各社が商標としている場合があります。














