アレー拡張処理を用いたミリ波レーダによる屋外人物の3Dイメージング
- ミリ波レーダ
- 3Dイメージング
- インフラセンサ
- 安全運転支援
- ドップラレーダ
安全で円滑な道路交通社会の実現に向けて、車両に搭載されたセンサからの情報に加えて道路交通インフラに設けたセンサからの情報を活用する路車協調システムに関する研究開発が推進されている。ミリ波レーダは雨・霧などの天候の影響を受けにくく、昼夜を問わず物標検出が可能なことから次世代のインフラセンサとして注目されている。人や車両が行き交う交差点などの環境において、ミリ波レーダを用いて様々な物標を分離検出し識別するには狭ビームによる3Dイメージングが有効である。3Dイメージングを行うには多数の受信アンテナから成る平面アレーアンテナが必要だが、単一のICチップではアンテナ数が不足し狭ビーム化が実現困難であった。また、複数のICチップを用いた場合、ハードウェアの複雑化やレーダ大型化の問題が生じる。
著者らは1チップのミリ波レーダに対してアレー拡張処理を用いることで仮想平面アレーの垂直・水平方向のアンテナ素子数を増加させ、狭ビーム化を実現した。屋外人物の3Dイメージングを行った結果、人物概形の検出が可能であることを確認し、物標識別性の向上を示した。
1. まえがき
近年の交通事故死者数は減少傾向にあり、警察庁によると2020年における24時間死者数(交通事故発生から24時間以内に亡くなった死者数)は3,000人以下にまで減少した1)。しかし、政府が第10次交通安全基本計画に掲げた、2020年までに24時間死者数を2,500人以下にする目標値には届いておらず、多くの人命が交通事故により失われている。より安全な道路交通の実現を目指し2021年に定められた第11次交通安全基本計画では、2025年までに24時間死者数を2,000人以下にすることを目標としている2)。また、政府の定める官民ITS構想・ロードマップ2020では、2030年までに「世界一安全で円滑な道路交通社会」の構築を目標に掲げており、安全なだけでなく交通渋滞を緩和し円滑な道路交通を実現することで環境負荷の低減にも貢献する社会の構築が望まれている3)。この目標達成に向けて路車協調システムを用いた自動運転に関する研究開発が推進されている。路車協調システムは、車両に搭載されたセンサからの情報に加えて、道路交通インフラからの情報を活用する。道路交通インフラに求められる要件として、車両から認識できない周辺車両や歩行者情報の取得が挙げられており、これらの情報を車両、及び運転手へ提供するセンサがインフラ側に必要とされている。
物標に電波を照射し、反射波から物標までの距離や速度を検出するミリ波レーダは、その性能が雨や霧などの影響を受けづらく、太陽光などの照明条件に左右されない特徴がある。そのため、上記の安全運転支援と円滑な交通を実現し得る次世代のインフラセンサとして注目されている。
著者らは交通状況の監視・制御を行うインフラセンサとしてミリ波レーダの開発を進めており、これまでに距離・速度・方位角情報から車両の位置を検出する2Dイメージングレーダに関する検討を行ってきた4)。さらに、開発を進める中でレーダによる物標検出をより高精度に行うため距離・速度情報と方位角・仰角情報を用いた物標の3Dイメージングに関する検討を行い5)、車両検出を目的とした道路監視だけでなく人や車両が混在する環境下での利用を考えている。本稿では、ミリ波レーダを用いた屋外人物の3Dイメージングの詳細について述べる。
2. ミリ波レーダの測定原理
2.1 距離・速度の測定
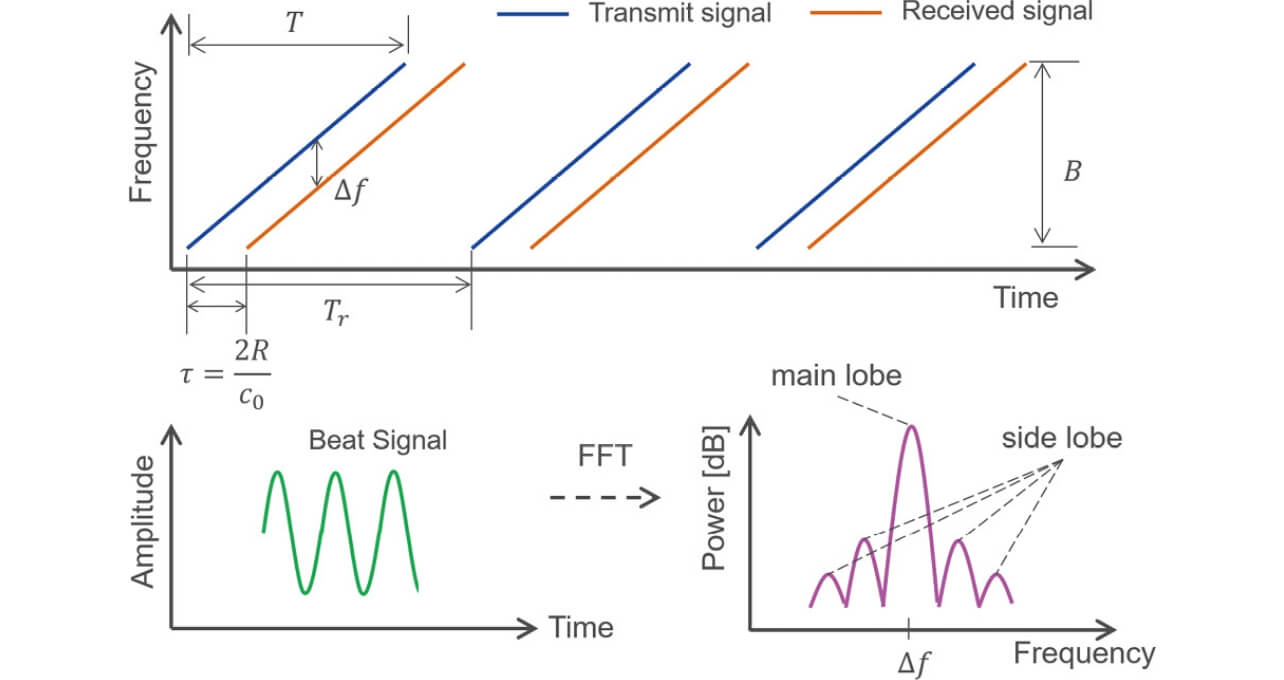
レーダ方式には様々な種類が存在するが、ここでは今回採用したFrequency Modulation Continuous Wave(FMCW)方式のレーダによる距離、速度の測定原理について説明する。FMCWレーダは図1に示すようなチャープ信号と呼ばれる周波数変調された信号を送信し、物標によって反射された受信信号と送信信号をミキシングすることで得られた差周波成分をもつビート信号を用いて物標までの距離R を測定する。受信信号はチャープ信号に対して、レーダと物標間の往復伝搬距離に応じて遅延して受信されるため、ビート信号の周波数Δf は遅延時間τ=2R ⁄ c0、すなわち物標との距離に比例し、次の関係が成り立つ。

ここで、B は掃引周波数帯幅、T は周波数掃引時間、c0は光速を表す。ビート信号をフーリエ変換し、周波数スペクトラムから物標応答に相当するピーク情報を読み取ることでレーダと物標間の距離を算出できる。また、物標が移動している場合、ドップラ効果によりレーダと物標の相対速度に応じた周波数成分(ドップラ周波数fd )が受信信号に重畳する。ドップラ周波数と相対速度v は次の関係が成り立つ。

ここで、f0はFMCWレーダで使用する中心周波数、λ0は中心周波数に対応する波長を表す。ドップラ周波数はチャープ信号の送受信を複数回行うことで得られる受信信号をフーリエ変換し、周波数スペクトラムのピーク情報を読み取ることで求めることができる。なお、検出可能な最大ドップラ周波数は送信周期Tr に依存し、送信周期が短いほど高いドップラ周波数を検出できる。サンプリング定理から一意に決定できる検出可能な最大ドップラ周波数は1/(2Tr )であり、対応する速度は(2)式のドップラ周波数と相対速度の変換時に生じる係数を適用したλ0 /(4Tr )である。
2.2 角度の測定
レーダが複数のアンテナからなるアレーアンテナで構成され、物標とレーダ間の距離がアレー開口よりも十分に大きい場合、レーダへの物標からの入射波は平面波とみなすことができる。このとき、レーダに対する物標からの反射信号は、受信アンテナごとにレーダと物標の相対角に基づいた経路長差をもって入射する。そのため、各受信アンテナにおける受信信号の間には、経路長差による遅延量の違い、すなわち位相差が生じる。この位相差をもとに、レーダの視線方向を基準とした際の物標の角度を算出することができる。角度の算出はアレーアンテナから得られた受信信号をフーリエ変換し、得られる周波数スペクトラムのピーク情報を読み取ることで得られる。図2に受信N 素子の等間隔リニアアレー(Uniform Linear Array,ULA)における各受信アンテナの経路長差を示す。
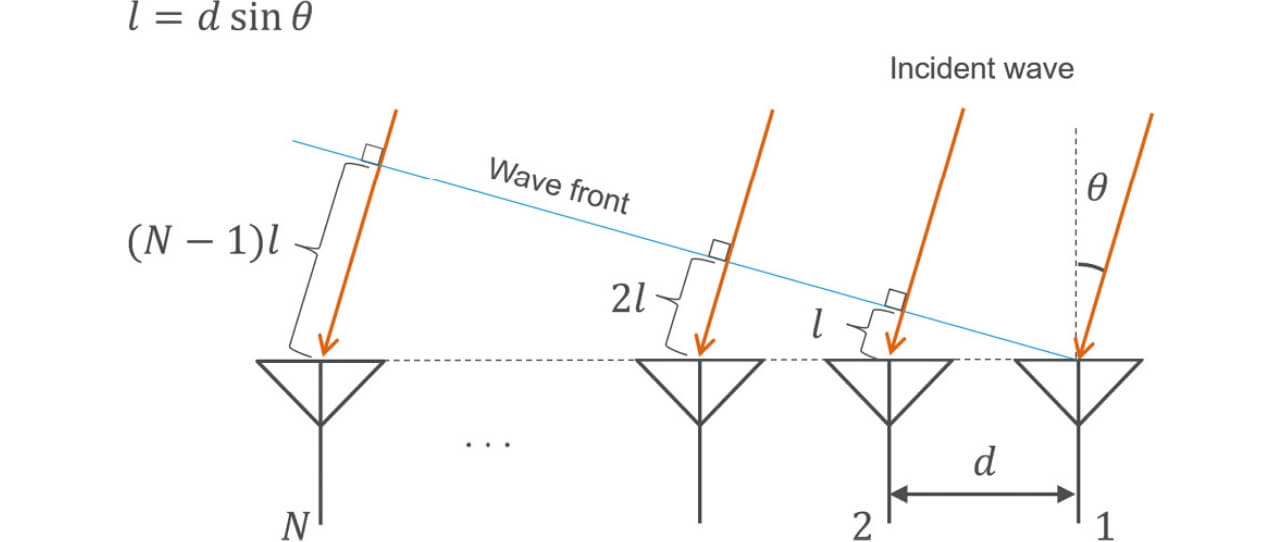
なお、ULAを水平方向に配置した場合は方位角を測定可能であり、垂直方向に配置する場合、仰角の測定が可能となる。方位角・仰角を同時に検出する場合はアンテナを平面上に配置した平面アレーアンテナを利用する。
3. 物標検出の高精度化に必要な機能
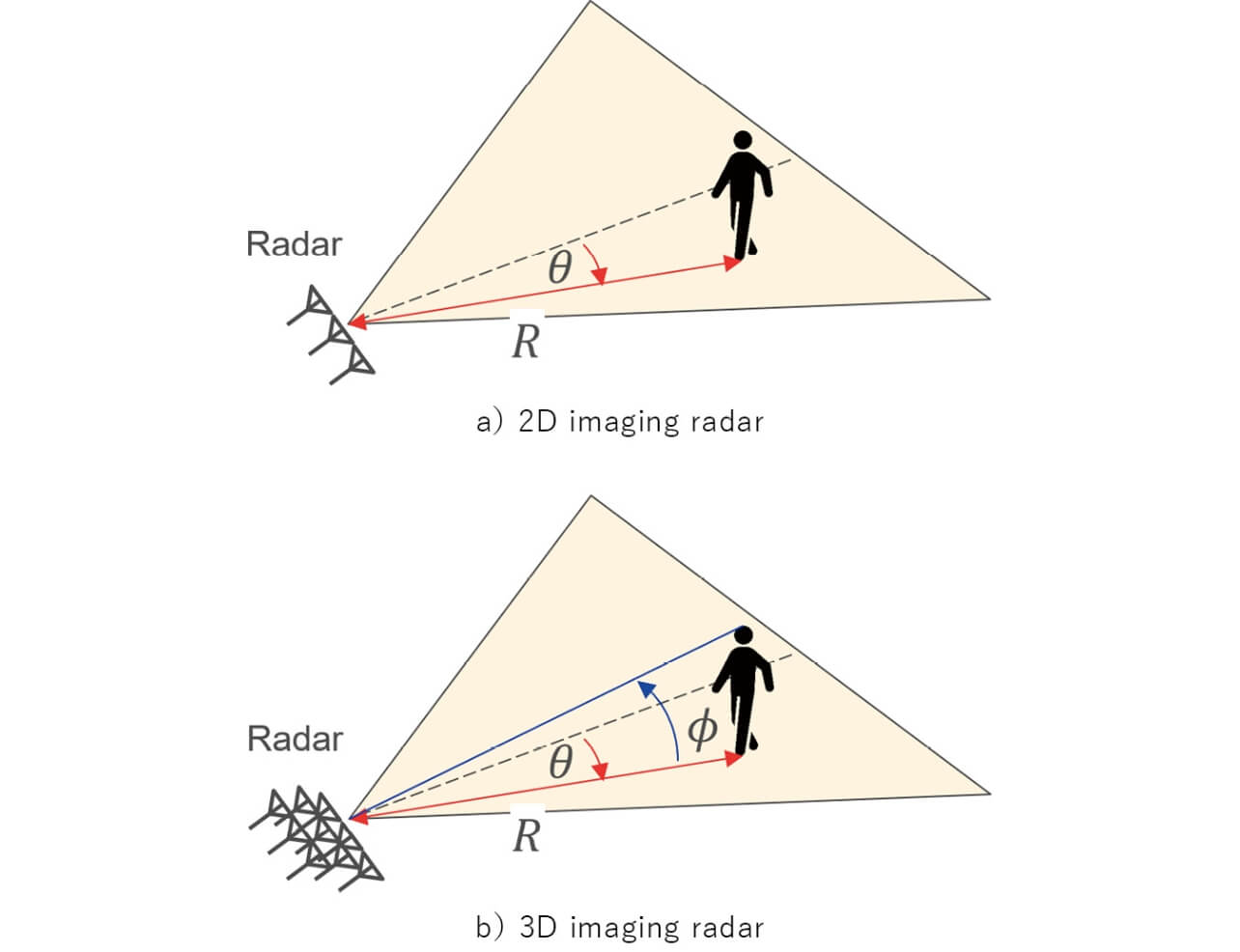
図3a)に示すように、距離・速度・方位角情報から物標位置を検出する2Dイメージングレーダでは水平方向に並ぶ受信アレーアンテナを有するレーダが使用される。ここで、R はレーダと物標間の距離、θ はレーダ視線方向と物標の成す角(方位角)を表している。また、距離・速度・方位角・仰角情報から物標位置を検出する3Dイメージングレーダでは図3b)のように受信アンテナに平面アレーアンテナを利用することにより2Dイメージングレーダで検出可能な距離・速度・方位角情報に加えて仰角φ を検出する。レーダを用いて交差点や車道の監視を行う際には、人物だけでなく車両や建造物・看板や標識など様々な物標からの反射波が受信される。従来の水平方向にアレーアンテナを備えたレーダによる距離・速度と方位角情報を用いた2Dイメージングでは、図4 a)のようにアレーアンテナの配置と同一の水平面内の物標位置・速度を検出する。しかし、物標の高度情報はこの平面上に射影されてしまい高度の異なる物標が同一平面内に検出される。そのため、垂直方向に広がりをもつ物標は形状の識別が困難になる。また、速度情報はインフラセンサにおいて車両接近による危険度や逆走の判断、速度超過の検出へ使用されると考えられるが、2Dイメージングレーダで検出可能な速度は同一平面内の値として検出される。レーダを高所に取り付けて地表の物標を観測する場合など、レーダの視線方向に対して物標の移動方向が異なるときは物標速度情報の測定精度が低下する。一方、3Dイメージングでは水平・垂直方向にアレーアンテナを備えたレーダを用いて、方位角だけでなく仰角を加えた到来角情報を測定する。距離・速度・方位角に加えて仰角情報を用いることで図4 b)のように物標の3次元空間分布情報(3Dイメージング)が取得可能になり、高度の異なる物標を分離して検出できるほか、レーダから見た3次元空間上の物標形状が把握可能になるため、物標識別や状態(人物の姿勢等)の判断が行いやすくなると考えられる。
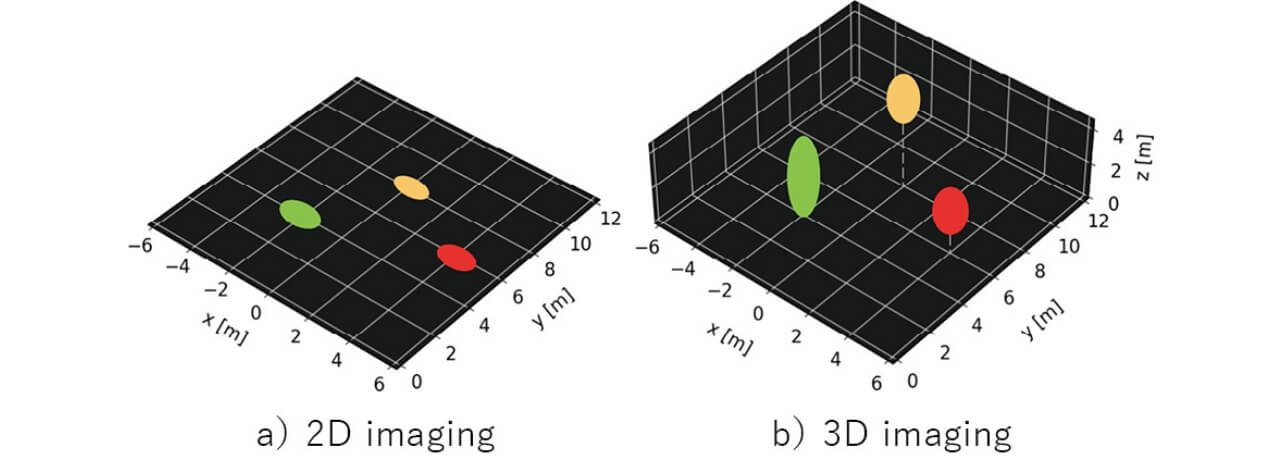
また、方位角に加え仰角情報を利用することで物標の速度情報を3次元空間に分解することが可能になるため、2Dイメージングレーダで問題であったレーダを高所に設置し地表の物標を観測するような場合に、より正確な物標速度の検出が可能になる。インフラセンサは車両側に搭載されたセンサでは検出が困難な物標の検出を行うため、高所に取り付けて地表を観測することが想定される。その際には、人物や車両等の反射波だけでなく周辺の標識や看板といった高さの異なる物標からの反射波を受信しやすいと考えられる。そのため、3Dイメージングによる高さでの分離、および方位角・仰角情報によって物標移動速度を分解し、より正確な情報を提供することが必要になる。
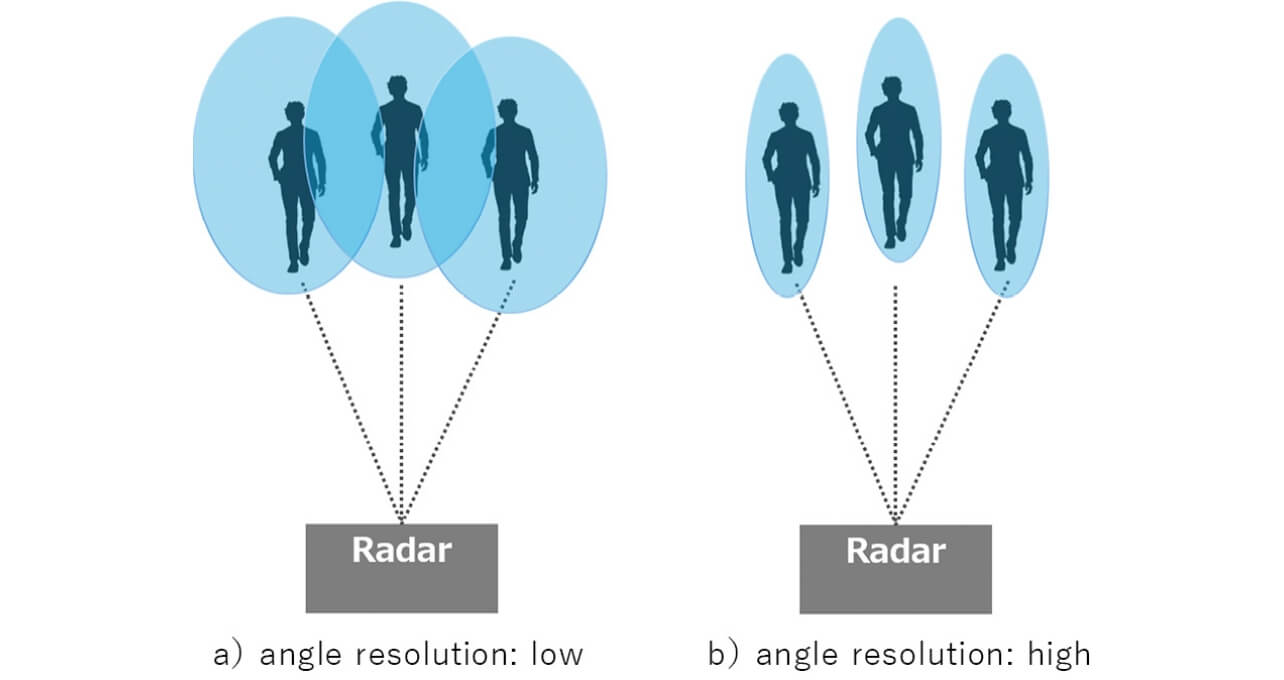
また、レーダの観測空間内に複数物標が存在する状況では、個々の物標位置を分離検出できるような狭ビーム化の実現、すなわち分解能の向上が必要になる。電波の反射から物標情報を検出するレーダは距離や速度を検出しやすく、距離分解能は周波数帯幅、速度分解能は観測時間を増加することで高めることができる。しかし、レーダから見た複数物標が近接して並走する場合において、距離や速度における分離は困難になる。中でも人物は車両よりも電波を反射しづらいため、図5のように複数人が近接すると距離や速度での分離検出が困難になる。したがって、人物や車両などの近接する複数物標を分離検出するには角度方向での狭ビーム化が必要になる。
以上のことから、レーダにより観測した物標を分離検出するには、距離・速度だけでなく角度方向の狭ビーム化が必要であり、高度の異なる物標を区別し、物標の形状や状態を識別するには3Dイメージングが有効であると考えられる。狭ビームによる3Dイメージングを行うには多数の受信アンテナ数を有する平面アレーアンテナが必要になる。しかし、現在のミリ波レーダのICチップは主に1チップあたり3つの送信アンテナと4つの受信アンテナで構成されるのが一般的であり、1チップではアンテナ数が不足し、狭ビームでの3Dイメージングが困難である。複数のチップを用いることでアンテナ数の不足を改善できるが、ハードウェア構成が複雑になる他、多数のアレーアンテナを用いることによりレーダシステムの大型化につながる。著者らはこの問題に対し、1チップのミリ波レーダにおいて次章で述べる狭ビーム化技術を適用して平面アレーアンテナを構成し物標の3Dイメージングを試みた。
4. 狭ビーム化技術
角度方向の狭ビーム化を実現するにはアレー開口長の拡大、すなわち受信アレーアンテナを構成するアンテナ素子数の増加が必要になる。しかし、アンテナ素子数の増加はレーダICチップによるアンテナ数の制約が存在するため、マルチチップ利用に伴うハードウェアの複雑化やレーダの大型化につながるといった問題がある。アレー信号処理には限られたアンテナ素子数で、受信アンテナ数を増やすことなくアレー開口長を拡大する様々な手法が提案されている。本章では狭ビーム化を実現する手法について説明する。
4.1 最小冗長アレー
最小冗長アレー(Minimum Redundancy Array,MRA)はアレー素子を不等間隔に配置するスパースアレーの一種である6)。MRAでは素子間距離の冗長度を最小にすることで同一素子数において最大の開口長を実現することができる。
4.2 Khatri-Rao積拡張アレー処理
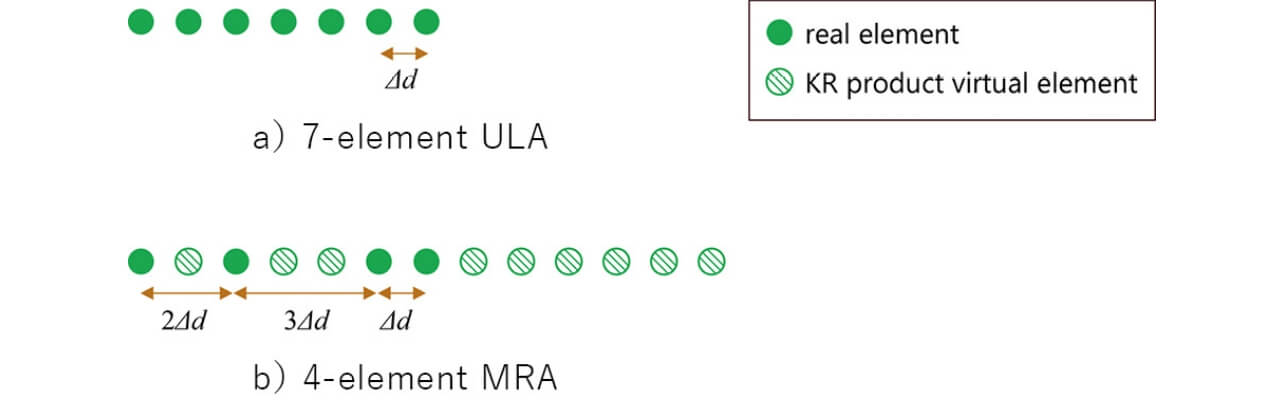
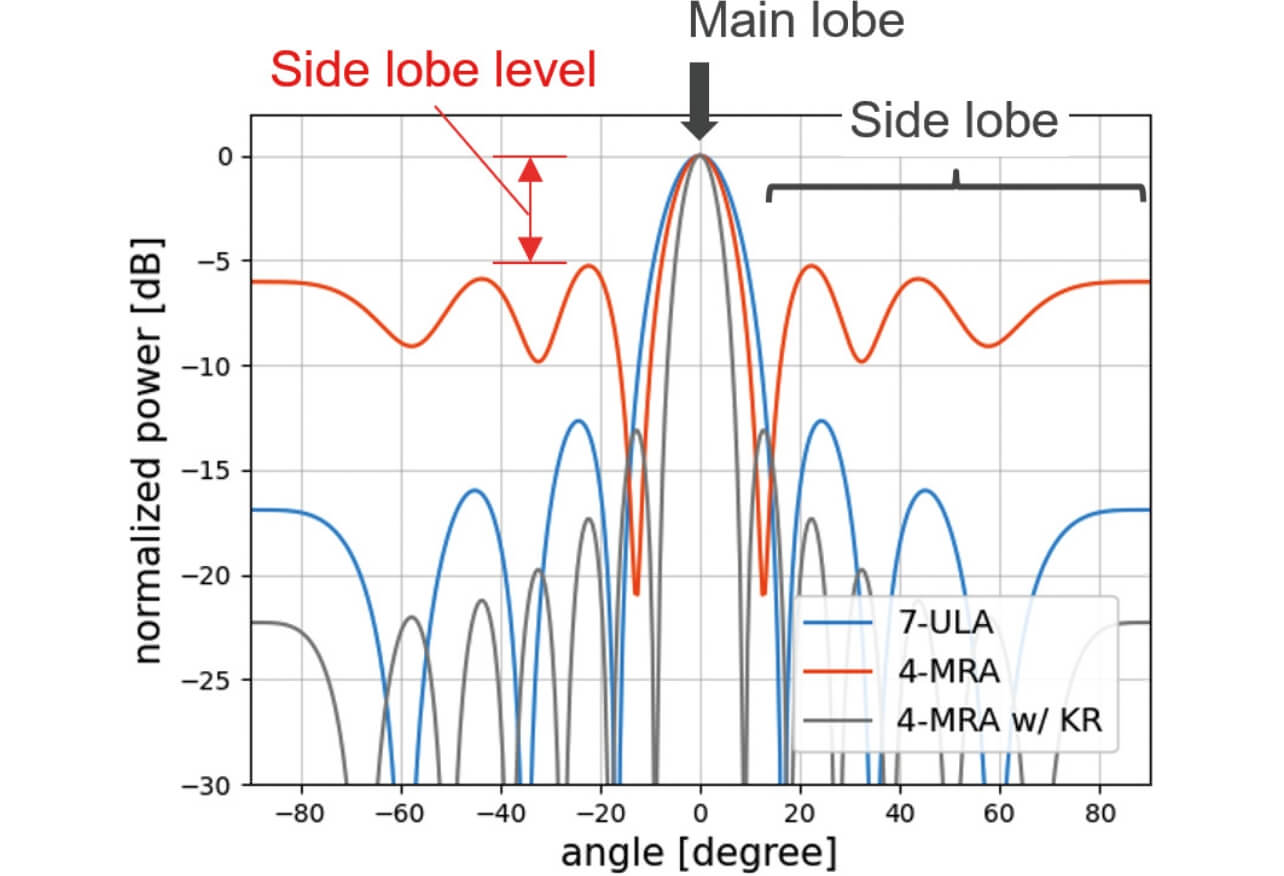
Khatri-Rao(KR)積拡張アレー処理はアレー開口長を仮想的に増加する手法の1つである7)。この手法はアレーデータの2次統計量である相関行列を利用しており、相関行列から非重複要素を抽出したものを仮想アレーデータとして使用する。平面波到来時において、アレーデータから算出する相関行列は2つのアンテナ素子間の距離差に対応する位相差が要素として現れる。一般に、平面波到来時のN 素子ULAに対してKR積拡張アレー処理を適用すると、2N -1素子の仮想アレーが得られることが知られている。また、この手法は等間隔アレーに適用するよりも、不等間隔アレーと組み合わせることで効率的に仮想アレー数を増加させることができる8)。これは不等間隔アレーにおける相関行列の非重複要素数がULAの場合よりも多くなるためである。不等間隔アレーとKR積拡張アレー処理の併用効果を計算機シミュレーションにより確認する。図6に計算機シミュレーションにおけるアレー配置を示す。ここで、Δd は最小受信素子間隔であり、本シミュレーションではΔd =3.79mmとした。これは79GHzを中心周波数とするミリ波レーダにおける半波長に対応する。はじめに0°からの1波到来時における受信アレーアンテナが7素子ULA、4素子MRA、および4素子MRAにKR積拡張アレー処理を適用した際の角度スペクトラムを図7に示す。4素子MRAの角度スペクトラムはサイドローブレベルが高いものの、メインローブ幅は7素子ULA相当となることが確認できる。また、4素子MRAにKR積拡張アレー処理を適用した場合、13素子ULAと同等の仮想アレーが得られるため、7素子ULAよりも狭ビーム化が実現可能となる。
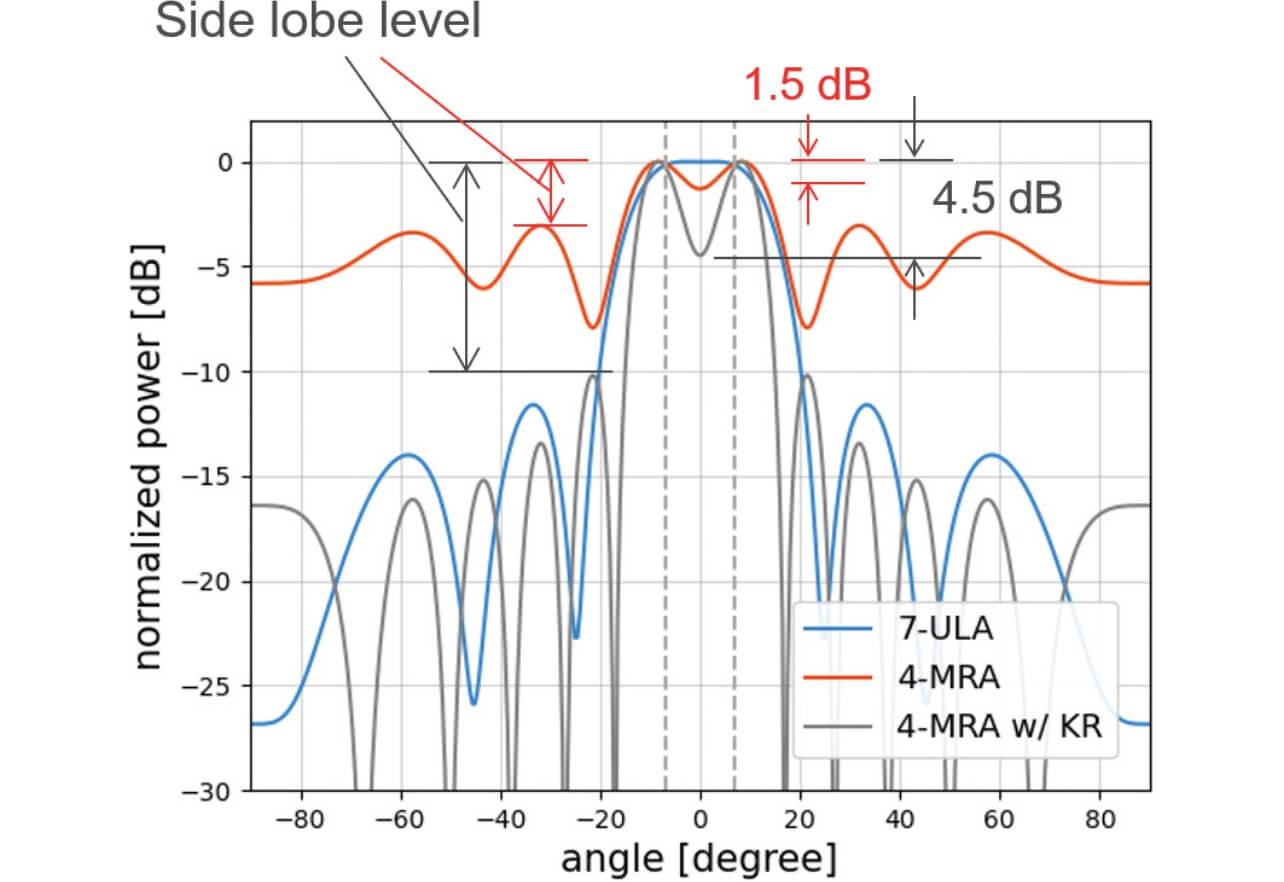
また、2波到来時の1例として±7°からの到来波における角度スペクトラムを図8に示す。ここで、到来波は等距離に位置する2物標からの同一振幅を持つ2波を仮定している。7素子ULAでは2波を分離できておらず、4素子MRAではKR積拡張アレー処理の有無にかかわらず2波を分離できている。しかし、KR積拡張アレー処理の有無により、2波のピーク間の落ち込みに違いが現れている。KR積拡張アレー処理を施さない場合は1.5dB、適用した場合では4.5dBである。実際のレーダによる測定ではアレーアンテナを構成するアンテナ素子のばらつきや到来波のSNRにより角度スペクトラムの形状が変化し、1~2dBのレベル差では分離できないことがある。これらのばらつきを加味し、角度の検出条件を最大ピーク値から3dB以上の落ち込みを有するピーク角度を検出すると考えたとき、KR積拡張アレー処理を適用したほうが2波を分離検出しやすくなる。また、サイドローブレベルに関しても4素子MRA(3dB)とKR積拡張アレー処理を適用した場合(10dB)で違いが現れており、上記の変動要因の存在を考慮すると4素子MRAではサイドローブを誤検出しやすいが、KR積拡張アレー処理を適用したほうがサイドローブとのレベル差は大きいためサイドローブの誤検出を防ぐための閾値の設定が容易になる。
4.3 Multiple Input Multiple Output(MIMO)レーダ
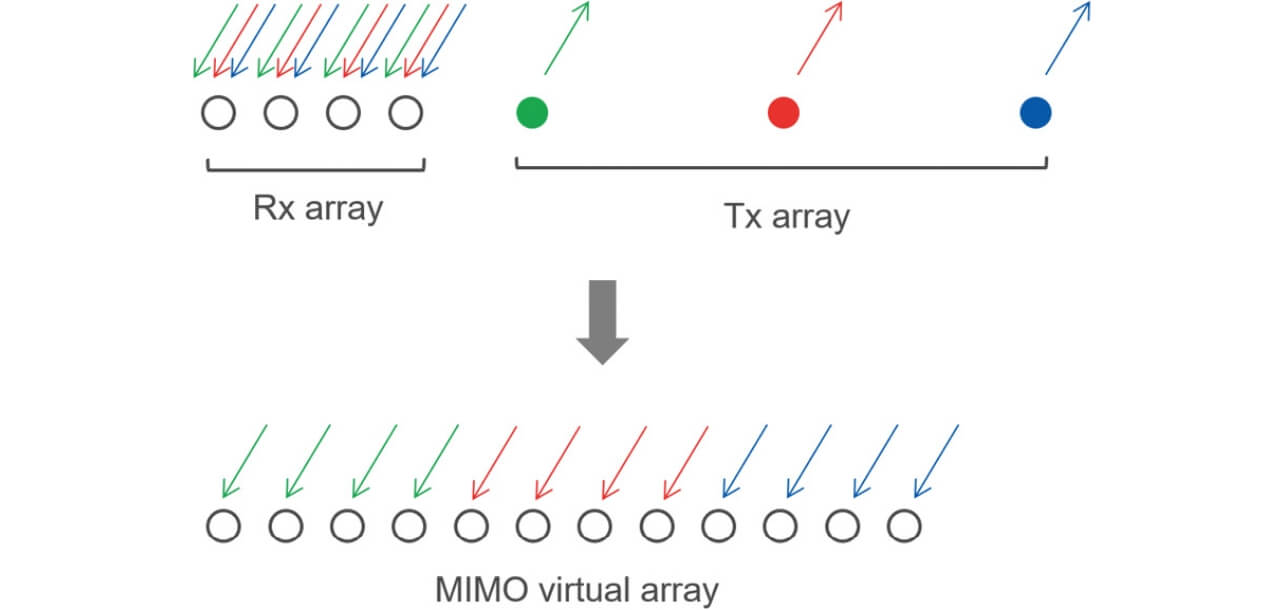
狭ビーム化は受信アレーアンテナのアンテナ素子数を増加することで実現できるが、多くの受信アンテナ数を必要とする。これは単一の送信アンテナに対し受信側をアレーアンテナとするSingle Input Multiple Output(SIMO)レーダ構成と呼ばれている。これに対して、送信アンテナのアレー化も行ったものがMIMOレーダ9)である。MIMOレーダにおいて受信アレーアンテナが受信する信号は複数の送信アンテナによる信号が重畳して受信される。受信アンテナ側ではこの信号を各送信アンテナによる信号ごとに分離し、結合することで仮想アレーを形成する。1例として、L 個の送信素子とM 個の受信素子から構成されるMIMOレーダを用いた場合、最大でL ×M 個の仮想素子が得られ、送信1個、受信L ×M 個のSIMOレーダと等価な仮想アレーを実現できることが知られている(図9はL =3、M =4の場合)。MIMOレーダを用いることで効率的にアレー素子数の増加(アレー開口長の拡大)が可能となり、角度分解能を向上できる。
これら最小冗長アレー、KR積拡張アレー処理及びMIMO化処理を併用することで、複数のチップを用いずに1チップの少ない実アンテナ素子数で効率的な大開口アレーを実現できる。また、使用するチップ数が少なく済むことにより、ハードウェアの複雑化をせずに平面アレーを実現できる。従来におけるこれらの仮想アレー技術の適用先は主に直線アレーであった。著者らはこれらの仮想アレー技術を直線アレーではなく平面アレーに適用することで、垂直・水平方向の仮想素子数を増加させ大開口平面アレーの実現を試みた。次章では仮想アレー技術をミリ波レーダに実装し、物標の3Dイメージングを行った実験結果について説明する。
5. 原理検証実験
4章で述べた狭ビーム化技術を実装したミリ波レーダを用いて3Dイメージングの原理検証実験を行った。本章では屋外人物の3Dイメージング結果について述べる。
5.1 ミリ波レーダのアレー素子配置
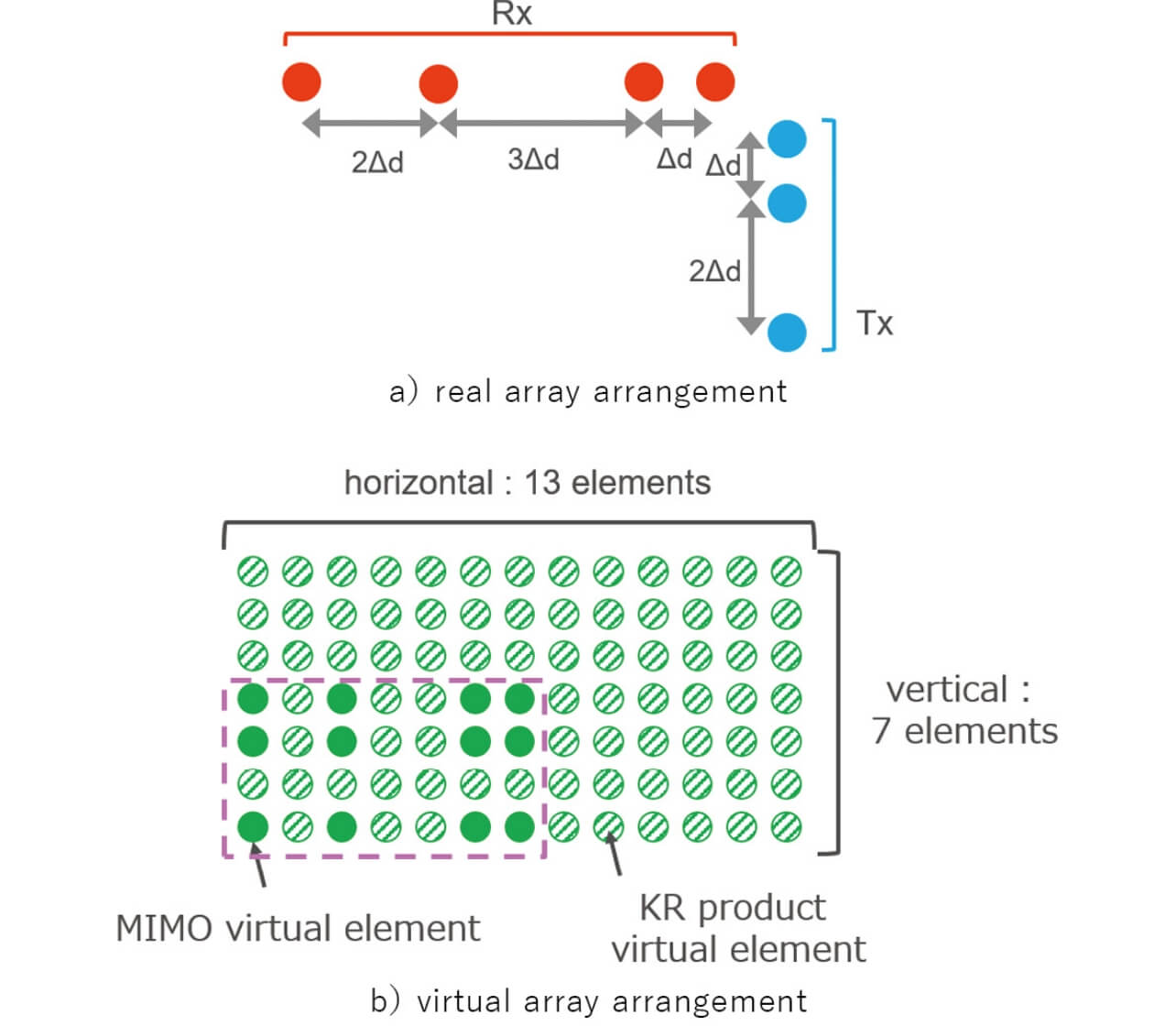
実験に用いたミリ波レーダの諸元を表1に示す。使用するミリ波レーダは送信3、受信4の1チップのFMCWレーダであり、時分割送信を行うことでMIMO仮想アレーを形成する(Time Division Multiplexing-MIMO,TDM-MIMO)。送信アレーと受信アレーは図10 a)のように互いに直交する最小冗長アレーとなるよう配置されている。この送受信アレー配置によるMIMO仮想アレーは図10 b)のように、計12素子からなる不等間隔平面アレーとなる。形成された仮想アレーは垂直・水平方向に対しそれぞれMRA配置となる。本稿では、この不等間隔平面アレーに対しKR積拡張アレー処理を適用し、垂直・水平方向の仮想素子数の増加を試みた。KR積拡張アレー処理は直線アレー(1次元データ)への適用を想定した処理であるが、平面アレーデータのように水平・垂直方向の2次元アレーデータを拡張するために水平・垂直方向それぞれに対して順番に適用することはできない点に注意されたい(直線アレーデータを用いて相関行列を計算すると他方の次元の位相情報が消えるため)。本稿では、平面アレーデータを一次元化して相関行列を計算し、非重複要素となる拡張アレーデータを抽出した後、再び平面アレーデータとして形成することで垂直・水平方向の位相情報を残したまま拡張平面アレーデータを得られるようにした。KR積拡張アレー処理を水平・垂直方向のアレーデータに適用することで、仮想アレー素子数は垂直7素子、水平13素子からなる計91素子の等間隔平面アレーが形成される。これらの仮想アレー技術の利用により、マルチチップによるハードウェアの複雑化を行わずに、IC1チップで仮想91素子から構成される平面アレーを構成可能となり、同受信アンテナ素子数の平面アレーアンテナ利用時に比べて約1/4の大きさで実現できる。
| 項目 | 仕様 |
|---|---|
| レーダ方式 | FMCW TDM-MIMO |
| 送受信ポート数 | 送信3、受信4 |
| 中心周波数f0 | 79GHz |
| 掃引周波数帯幅 | 2.5GHz |
| 空中線電力 | 10dBm |
| 最小素子間隔Δd | 3.79mm |
| 最大検知速度 | ±32km/h |
5.2 実験条件
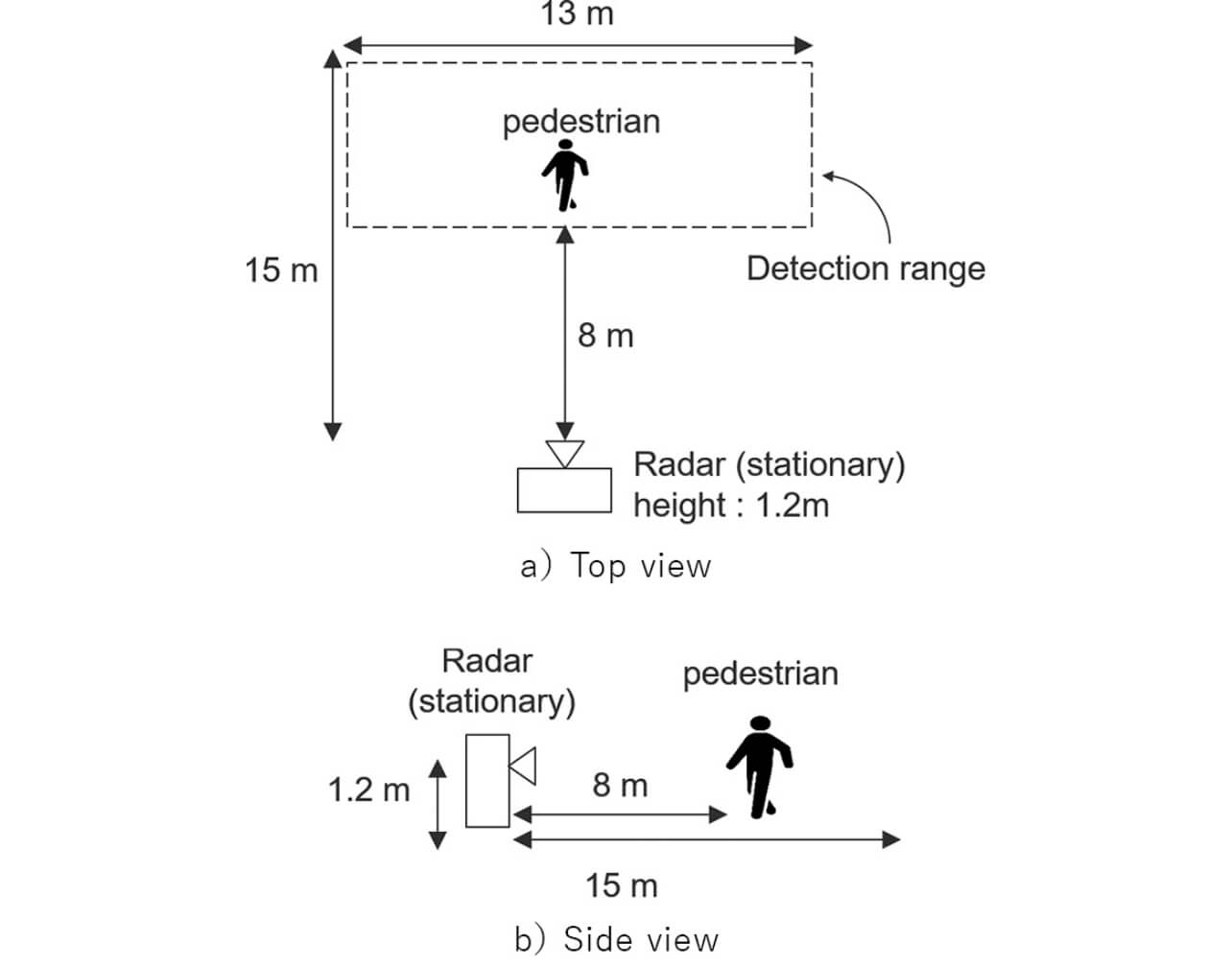
図11に示すような、幅約13m、奥行約15mほどの開けた屋外環境で歩行者の測定を行った。ミリ波レーダによる3Dイメージングの原理検証として、本実験では人物からの主な反射が胴体部からであると想定し、レーダは地上から約1.2mの高さに設置した。また、歩行者はレーダから約8m以上離れた領域を自由に動き回るものとした。なお、車両用信号機(法令で4.5m以上の高さに設置することが定められている)近傍に地表を見下ろすような角度(俯角45°)でインフラセンサを設置すると考えたとき、少なくとも地表に位置する物標とは約6.4m以上の距離が存在する。本実験ではミリ波レーダの設置高は異なるものの、レーダ・人物間の距離は高所に取り付けた場合と類似の信号が得られるものと想定しデータを取得した。
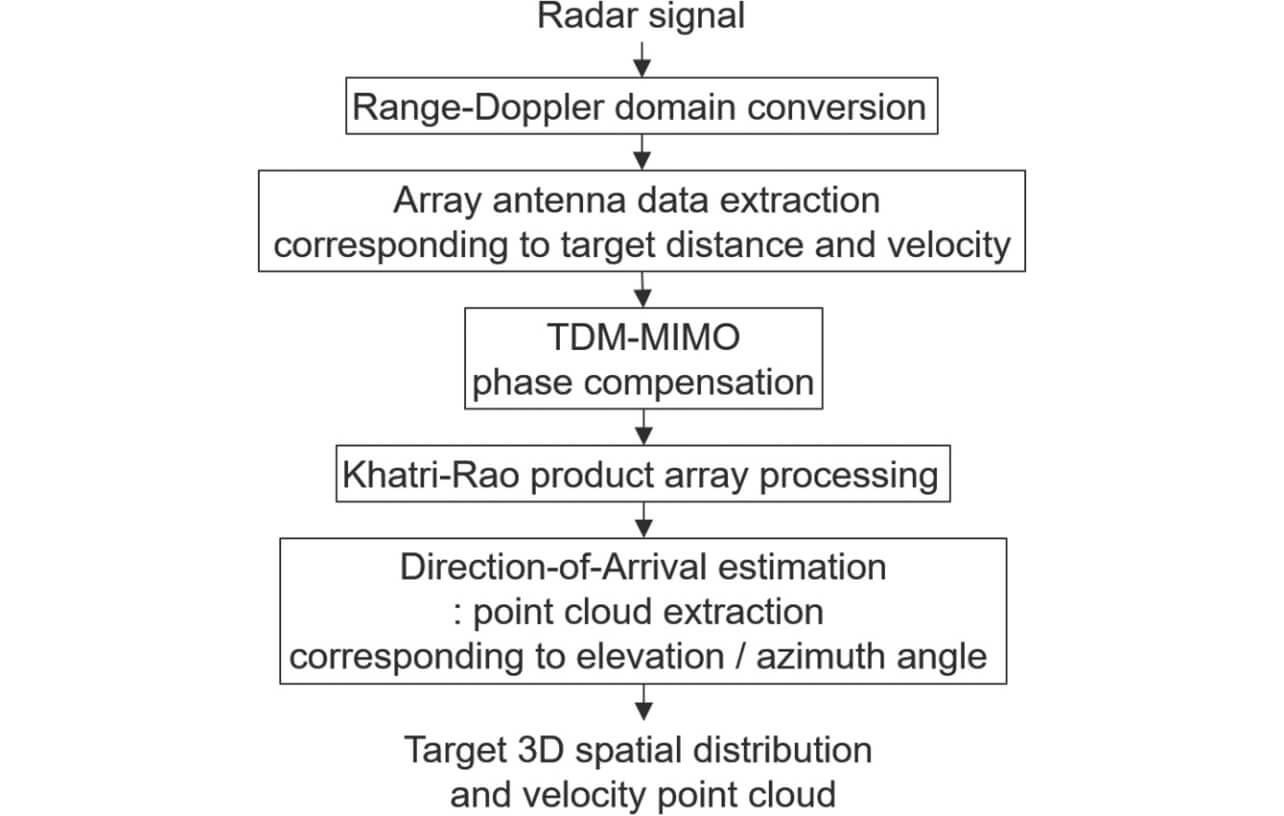
また、ミリ波レーダによる物標検出はレーダ受信信号を周波数領域に変換した周波数スペクトラムからピーク近傍の距離・速度・角度情報を点群として抽出することで位置情報を求める。図12に点群抽出フローを示す。はじめにレーダ受信信号に対してレンジ・ドップラ推定によりレーダ受信信号を周波数領域に変換し、周波数スペクトラムの強度情報をもとに物標の距離、速度に応じたアレーアンテナデータを抽出する。次に、抽出したアレーデータに対し、TDM-MIMO化処理に伴う位相補正を行う。この処理では、時分割送信における物標移動により生じるドップラ周波数を補正する。その後、KR積拡張アレー処理を適用し、到来方向推定を行うことで仰角・方位角情報を点群として抽出する。この点群情報から物標の3次元空間分布を得る。
5.3 人物1名のイメージング結果
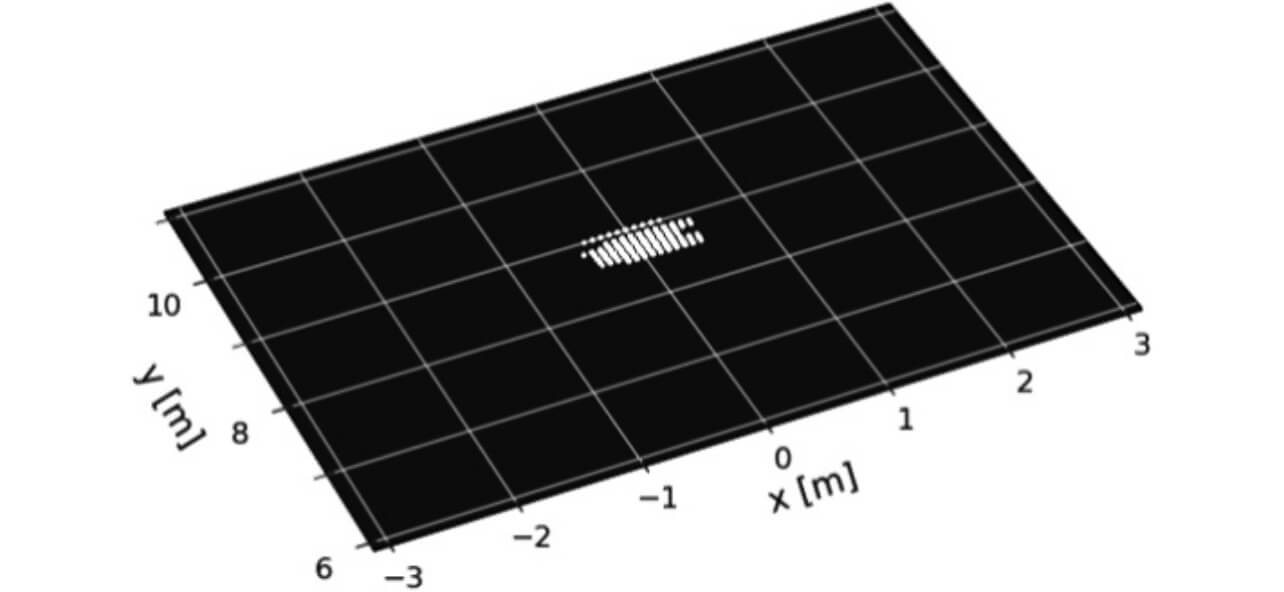
ここでは従来の距離と方位角による2Dイメージングと、距離・方位角・仰角による3Dイメージングの比較結果を示す。測定対象は、レーダ正面方向から約8~10m離れた距離に位置する歩行者1名とした。送信1素子、受信4素子を用いた際の2Dイメージングによる点群出力結果を図13に示す。レーダから約9m離れた地点に人物に相当する点群を検出できている。しかし、2Dイメージングでは人物位置を特定できるものの、高さに関する情報はレーダ視線方向上の平面内に重畳して検出されていることが分かる。
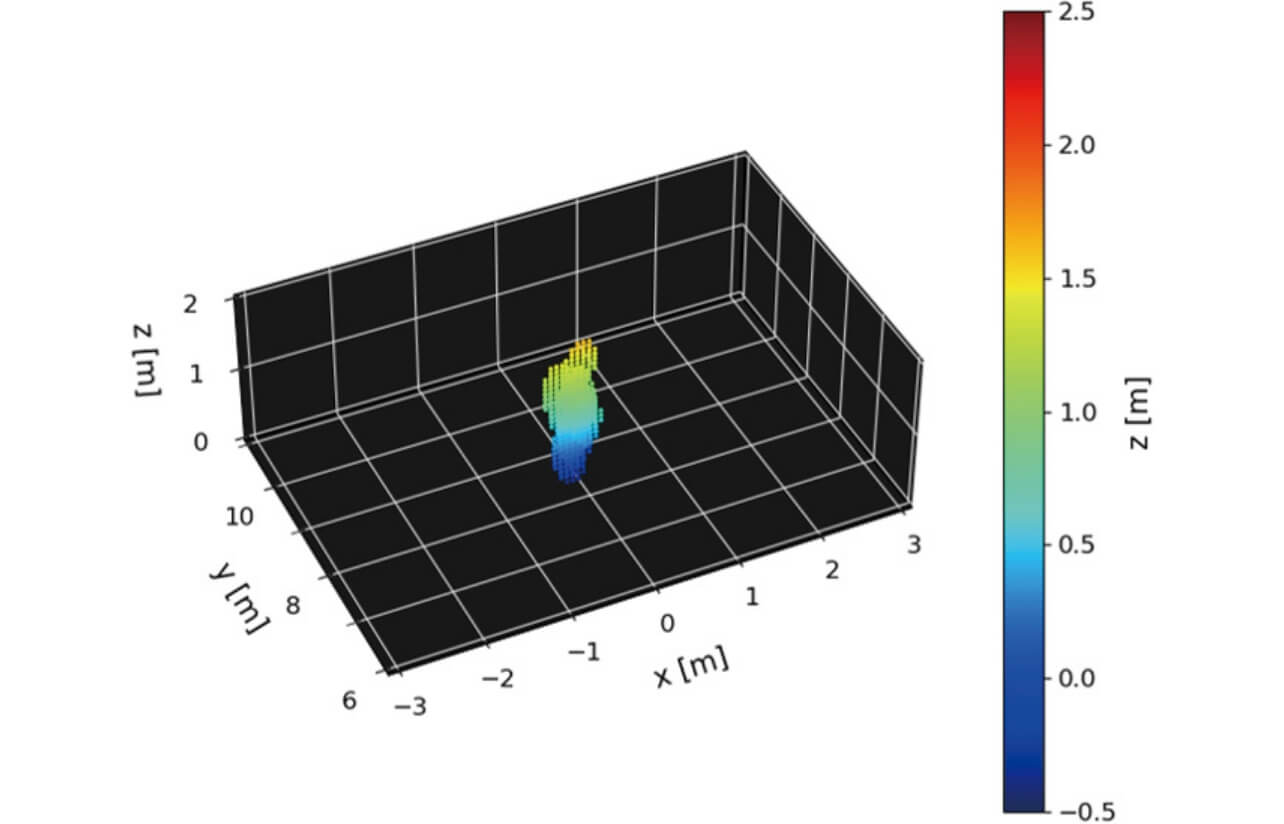
次にKR積拡張アレー処理を適用した3Dイメージングによる点群出力結果を図14に示す。3Dイメージングでは約1.5mの高さを有する点群が検出されている。これは主に人物の胴体部位に対応する点群検出が行われたと考えられる。一方で、手足の識別はできない結果となった。この理由として、手足は胴体に比べて反射が小さいため、胴体の反射と混合して検出されたと考えられる。したがって、本レーダでは手足などの上肢・下肢の検出は難しいが人体の概形は検出可能であることを確認した。
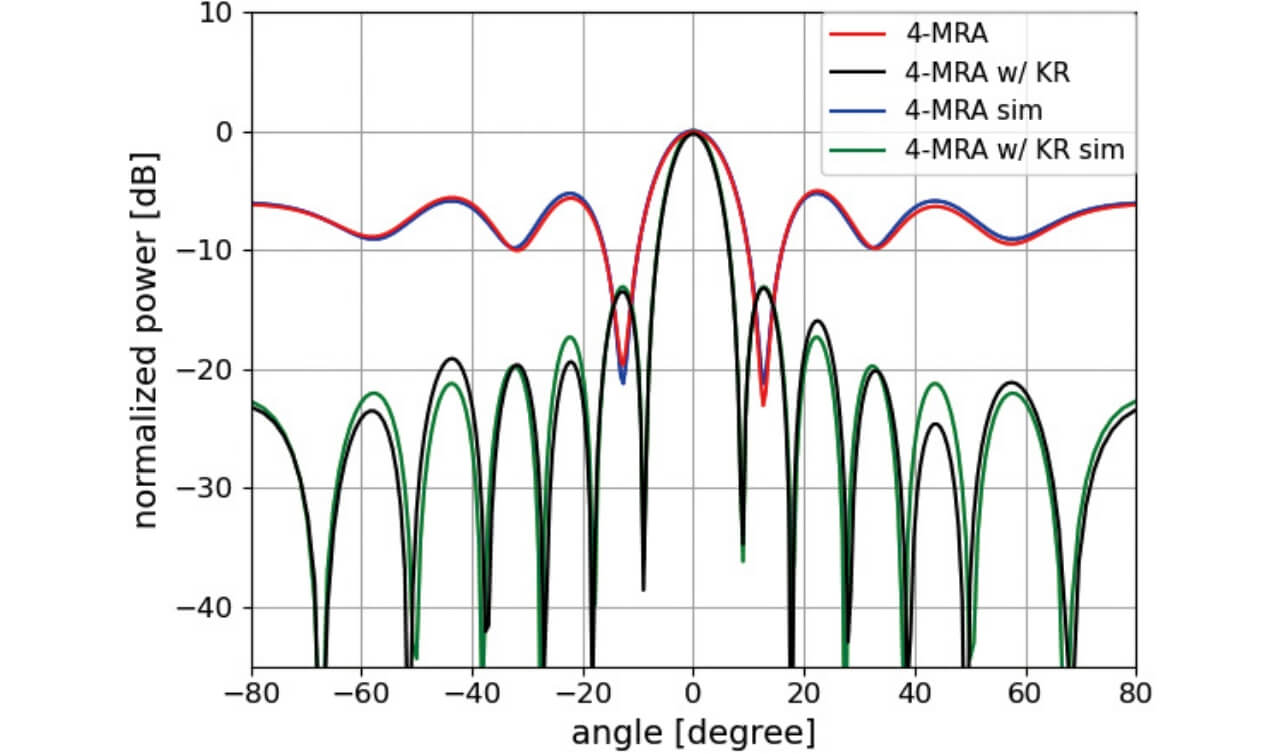
また、点群を検出した距離のレーダ正面(仰角0°)における方位角方向の角度スペクトラムを図15に示す。なお、図中には図7の4素子MRA及びKR積拡張アレー処理を適用した計算機シミュレーション結果(4-MRA sim、4-MRA w/ KR sim)も共に示している。4.2節で述べたように、KR積拡張アレー処理によって仮想的にアレー開口長が拡大されたことで狭ビーム化が実現されていることが分かる。なお、実際の測定結果ではアンテナばらつきや到来波のSNRの違いにより計算機シミュレーション結果とは角度スペクトラムの落ち込み(ヌル点)や一部のサイドローブに関して差が存在するが、点群検出で重要となる人物位置の0°近傍のスペクトラム形状(メインローブ)は計算機シミュレーション結果と0.3dB以下の差となっており、同等の結果が得られた。
5.4 複数人物のイメージング結果
前節において1名時の3Dイメージング結果から提案技術による角度測定における狭ビーム化効果を確認した。インフラセンサ応用では複数の人物が観測シーンに含まれることが想定される。本節では、複数人物の観測シーンの1条件として歩行者3名を対象とした3Dイメージング結果について述べる。人物1名測定時と同様に、レーダは高さ1.2mの位置に固定し、レーダ正面方向から8~10m離れた位置で任意の方向に移動する歩行者3名を測定した。図16にKR積拡張アレー処理を適用した3Dイメージングによる点群出力結果を示す。
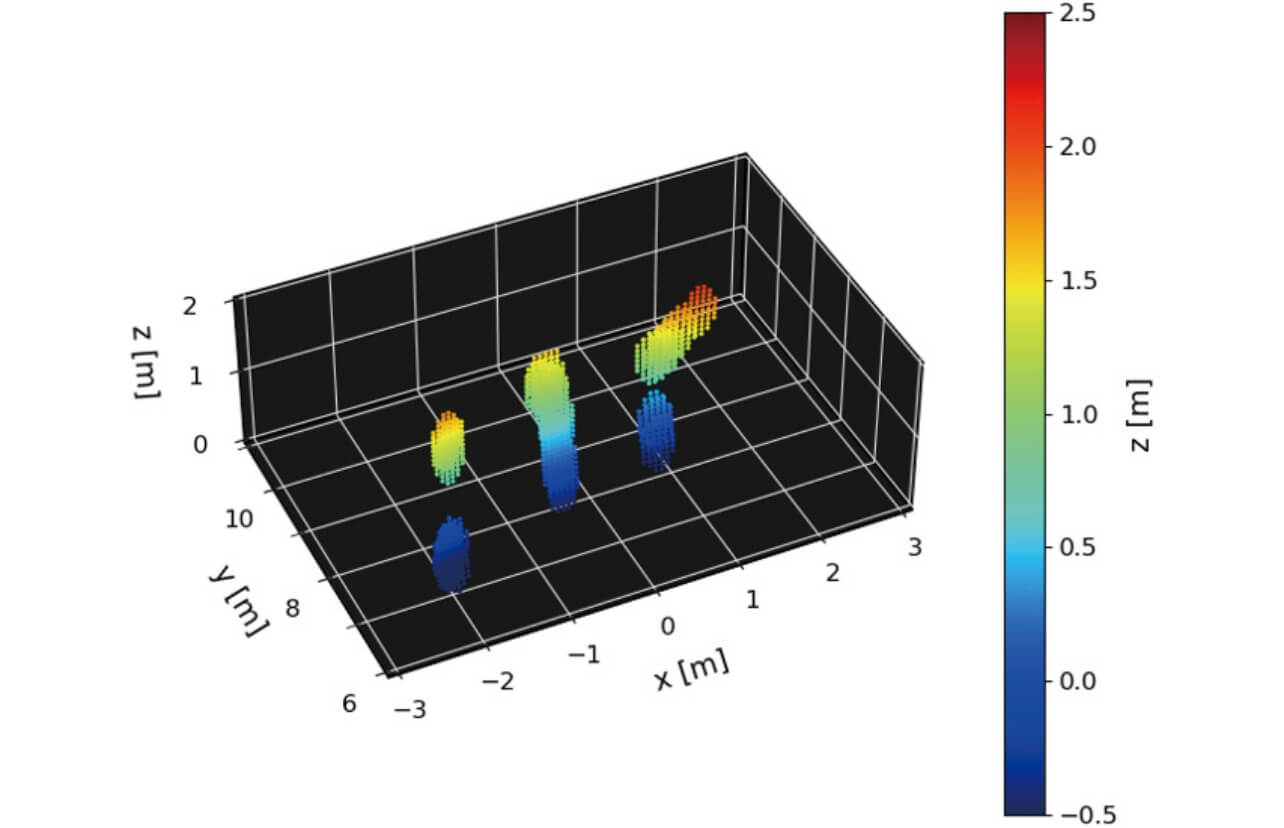
結果より、約1.5m間隔の3人の位置に対応した点群が分離検出されており、それぞれ胴体部からの反射成分を主とした人体概形を検出していることが分かる。ここで、点群の形状に違いが見られるのは測定シーンにおいて、レーダから見た3人の体の向きによるレーダ散乱断面積(RCS)の違いが一因として考えられる。また、図17に点群位置情報を速度情報と紐づけた結果を示す。ここで、色付けはレーダへ近づく方向の速度をマイナス、遠ざかる方向の速度をプラスとしている。結果よりレーダから見た視線方向の速度として2人が遠ざかる方向、1人が近づく方向の速度で移動していたことが分かる。
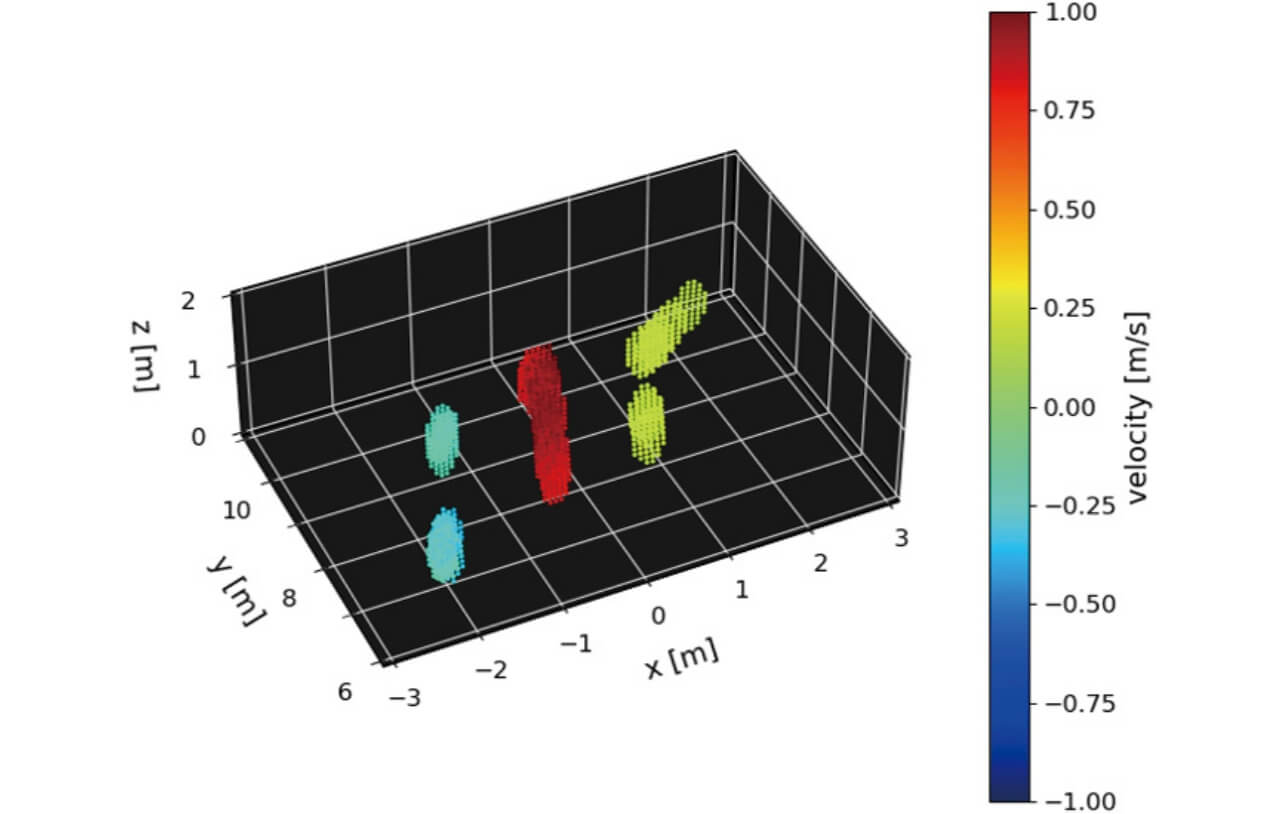
したがって、ミリ波レーダによる3Dイメージングから得られた点群位置・速度情報より、高さ約1.6m相当の3物標が秒速1m(時速約3.6km)以下の速度で移動している状態を観測しており、この物標が人物で歩行している状態である、と推察することができる。これら3次元空間分布の位置情報(高さや幅)、移動速度、時間変化による点群変化を観測することで検出物標の識別、及び物標の状態(歩く・走る等の歩行状態や転倒による変化など)を識別可能になると考えられる。なお、本検討では3Dイメージングによる人物の点群検出を確認するための基礎検証として、ミリ波レーダは人物からの反射が得やすいと想定される胴体部の高さに合わせた1.2mに設置して測定を行った。インフラセンサとしての使用が想定される高所に設置し、複数人が様々な速度(駆け足や低速歩行、自転車乗車時など)で観測シーンに含まれる場合や、人物だけでなく車両や建造物が混在する状況下での3Dイメージングについては今後の検討内容としたい。
6. むすび
本稿では、ミリ波レーダをインフラセンサとして利用することを想定し1チップの制約下で実現可能な平面アレーアンテナを構成し、屋外人物の3Dイメージングに関する検証実験を行った。1チップ利用による3送信、4受信の少ないアンテナ数であっても、最小冗長配置やMIMO化処理、KR積拡張アレー処理を利用することで大開口の仮想平面アレーを実現し、3Dイメージングにより手足などの識別は難しいものの、人体概形に対応する点群が得られることを確認した。この結果から3Dイメージングは従来の2Dイメージングに対して点群の高度情報を利用することで物標判別の向上が可能なことを示した。また、複数人の観測シーンの1例として歩行者3名の3Dイメージングを行い、8~10mの距離に位置する各人物(約1.5m間隔)の概形を点群として検出可能であることを確認し、点群の速度情報から状態識別の可能性を示した。
今後の検討課題として、路上であり得る様々な速度(駆け足や低速歩行、自転車乗車時など)で移動する複数人物の観測シーンや車両や建造物が人物の近傍に位置する際の観測シーンなど、RCSの異なる物標が存在する状況で高所にレーダを取り付けて観測し、性能評価を実施する。また、物標追尾に関する検討を行い、点群の形状や動線情報などの時間変化を組み合わせることで各物標の状態識別性の向上に関する検討を行い、ミリ波レーダの物標測位・識別性能を高めていく。
参考文献
- 1)
- 交通局交通企画課.“令和2年中の交通事故死者数について”. 警察庁.2021-01-04. https://www8.cao.go.jp/koutu/kihon/keikaku11/senmon/k_4/pdf/s2.pdf,(参照2021-03-12).
- 2)
- 中央交通安全対策会議.“交通安全基本計画”.内閣府.2021-03-29. https://www8.cao.go.jp/koutu/kihon/keikaku11/pdf/kihon_keikaku.pdf,(参照2021-04-02).
- 3)
- 官民データ活用推進戦略会議.“官民ITS構想・ロードマップ2020”.内閣府.2020-07-15. https://cio.go.jp/sites/default/files/uploads/documents/its_roadmap_2020.pdf,(参照2021-03-16).
- 4)
- 谷本雄大,上野大,齋藤啓介.広角度分離分解能を有する到来方向推定を導入した交通監視用ミリ波レーダ.OMRON TECHNICS.2020, Vol.52, p.41-46.
- 5)
- 谷本雄大,大橋卓,齋藤啓介.“ミリ波最小冗長MIMOレーダによる屋外人物検出”.2020年電子情報通信学会ソサイエティ大会.2020, p.137, B-1-137.
- 6)
- Moffet, A. T. Minimum-Redundancy Linear Arrays. IEEE Trans. 1968, Vol.AP-16, No.2, p.172-175.
- 7)
- Ma, W. K.; Hsieh, T. H.; Chi, C. Y. DOA Estimation of Quasi-Stationary Signals With Less Sensors Than Sources and Unknown Spatial Noise Covariance: A Khatri-Rao subspace Approach. IEEE Trans. 2010, Vol.SP-58, No.4, p.2168-2180.
- 8)
- 山田寛喜.ミリ波レーダによる高分解能イメージング技術.電子情報通信学会論文誌B.2021, Vol. J104-B, No.2, p.66-82.
- 9)
- Li, J.; Stoica, P. MIMO Radar Signal Processing. John Wiley & Sons, 2009, p.235-242.
本文に掲載の商品の名称は、各社が商標としている場合があります。














