機械学習を用いた外乱補正による加工精度向上の検討
- AI技術
- PLC
- フィードフォワード制御
- 外乱補正
- サーボプレス機
製造現場では生産性を維持・向上しながら加工精度を向上することが要求されている。それに伴い近年では、製造現場での材料や機械のばらつき・変動が無視できなくなっている。
製造現場では、このような外乱影響を抑制するために様々な制御手法の工夫や、現場作業者による生産装置の調整を行うことで加工精度の悪化防止に取り組んでいる。
一般に外乱影響の抑制にはフィードバック・フィードフォワード制御が用いられているが、フィードバック制御は外乱による影響が現れてから補正を行うため、効果が不十分となる場合がある。また、数式モデルを用いた外乱補正を行うフィードフォワード制御の場合、使用環境に依存するような制御対象では予測誤差が大きくなり、加工精度が悪化するという問題がある。
そこで、本論文では機械学習を活用した外乱補正による加工精度の向上手法について提案する。提案手法をサーボプレス機の下死点補正制御に用い、従来手法に対してMSE(平均二乗誤差)が1/6となる加工精度の向上を確認した。
1. まえがき
製造現場では生産性を維持・向上しながら加工精度を向上することが要求されている。それに伴い近年では、製造現場での材料や機械のばらつき・変動(以降、2M変動)のような外乱の影響が無視できなくなっている。例えば、プレス加工では加工精度が品質特性として特に重要視されている。プレス加工における加工精度は主に材料板厚のばらつきや製造装置の状態変化が影響し、加工精度が悪化した際には、製造装置の調整を行うことで加工精度の改善を行っている1)。
一般に外乱影響の抑制には、フィードバック・フィードフォワード制御が用いられる。しかし、フィードバック制御は与えた操作量の結果から補正を行うという原理上、外乱による影響が現れてからしか補正を行うことが出来ないため、不良品の発生に繋がる。また、フィードフォワード制御は外乱による影響が現れる前に、影響を抑えるように補正を行うための適切な補正量が必要となる。しかし、外乱補正に数式モデルを用いる場合、2M変動のような使用環境に依存する制御対象への適用は、予測誤差が大きくなり加工精度の悪化に繋がる。
このような背景から反復学習制御により、外乱影響を抑制する補正を行い、製品の加工精度悪化を防止する手法が検討されている2)。反復学習制御は、同様の条件が繰り返される場合において試行を繰り返すことで性能を向上可能な手法である。しかし、装置劣化や加工による温度上昇等のような経時変化する外乱に対しては原理上学習が進まず、外乱補正は困難となる。
そこで本稿では、従来手法の課題を克服した、機械学習を活用した外乱補正手法を提案する。本提案手法により、経時変化する外乱を含む、2M変動による製品の加工精度の悪化を事前に防ぐことができる。
本実験では、提案手法を弊社製AI搭載マシンオートメーションコントローラ3)(以降、AIコントローラ)に実装して効果を確認した。AIコントローラはマシンオートメーションコントローラに製造装置の制御とAI技術が共存し、時系列データの収集、特徴量算出、外れ値検知機能を持つ。
2. 課題
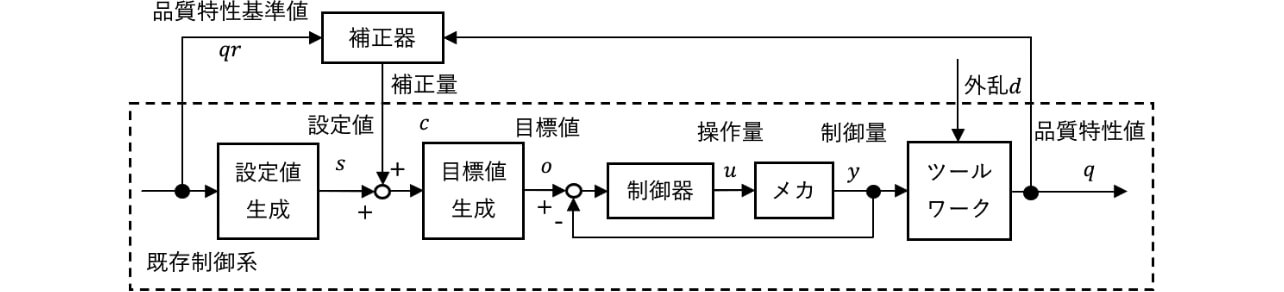
2M変動の複数外乱d が加工部のツール・ワークに印加されるフィードバック制御系を図1に示す。本稿での外乱は従来手法では対応できない経時変化するものも含む。品質特性基準値qr から加工機の設定値s を生成し、品質特性値q をフィードバックし、目標値生成から目標値o を出力する。制御器は目標値o と制御量y から操作量u を出力してメカを制御し、ツールを通じてワークの加工を行う。フィードバック制御系の場合、品質特性値q を用いて自動または手動で目標値の調整を行い、品質特性値q のばらつきが小さくなる制御を実現する。しかし、フィードバック制御系では外乱の影響が品質特性値q に現れてから設定値s の補正が行われる。そのため、加工材の個体差や気候や季節、日時のような同一条件とすることが困難な使用環境の差によっては、即座に適切な補正が行われず、良好な品質特性値q が得られない。
このため本稿では図2のようにツール・ワークに印加される2M変動の外乱d を入力、補正量c を出力とする補正器を用い、設定値s を補正するフィードフォワード制御系を考える。
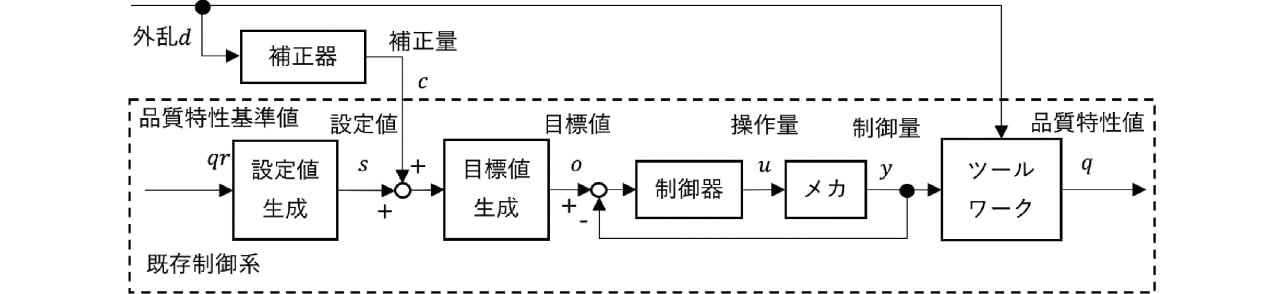
補正器には製造時に起こりうる2M変動の外乱d に応じた、品質特性値q のばらつきが小さくなる適切な補正量c を出力することが求められる。しかし、2M変動の外乱d は使用環境に大きく依存し、経時変化するため、一般的な数式モデルを用いた外乱補正を行うフィードフォワード制御や反復学習制御は適用できない。
そこで、フィードフォワード制御において困難となる補正器の設計を、機械学習を用いて容易に設計する手法について以降で説明する。
なお、外乱は十分に小さければ品質に影響は無く、極めて大きいと制御系での補正は不可能となることは自明である。そこで、本稿では2M変動の外乱d は、不良品を発生しうる大きさがあり、かつ、制御系の設計で想定されている範囲は越えないものと想定する。
3. 提案手法
3.1 補正器の構成
図3に提案手法となる補正器の構成を示す。補正器は特徴量演算部と予測器からなり、計測した2M変動の外乱d から適切な補正量c を予測する構成とする。
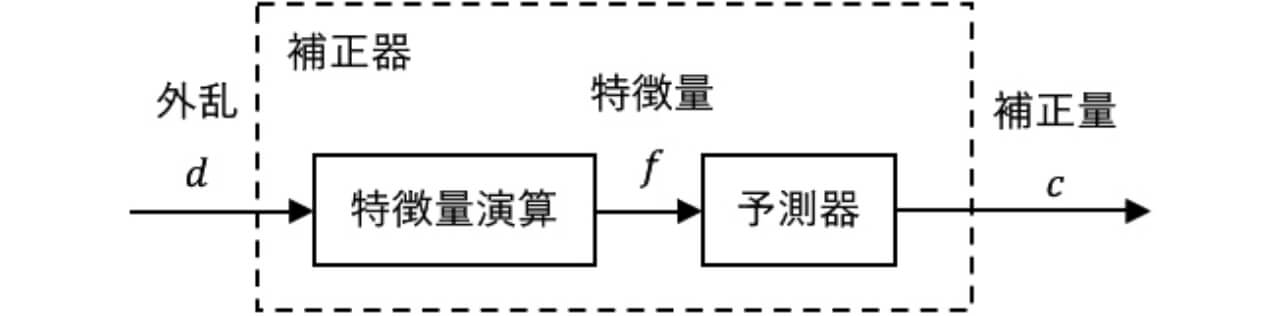
特徴量演算部は、品質特性値に影響を与える2M変動の外乱d をセンサで計測し、平均値、最大値等の特徴量化を行う。予測器は教師あり学習アルゴリズムを用いた予測モデルにより特徴量f に応じて補正量c を出力する。
3.2 補正器の構築手順
補正器の構築ではまず、従来手法(熟練者による設定やフィードバック制御等)による生産データ(補正量c 、センサで計測した2M変動の外乱d 、および品質特性値q )の収集を行う。なお、品質特性値q を制御に用いないにもかかわらず、収集する理由について補足する。収集したデータは、従来手法に基づくため必ずしも良品ではなく、不良品のデータも含まれる場合がある。また、良品であっても品質特性値にはばらつきがあり、規格上下限に近いデータも含まれている。そのため、収集したデータ全てを学習データとして用いると品質特性値q が大きくばらつく補正量c を出力する予測モデルとなり、加工精度の向上は見込めない。そこで、データ前処理で、収集したデータの中から品質特性値q のばらつきが小さいデータセットを選別して学習を行う。なお、予測器の学習はオフラインにて行い、生成した予測モデルおよびデータ前処理で選択した特徴量f の演算を制御装置に実装する。
- (1)
- データ収集
従来手法で製造した際の品質特性基準値qr 、品質特性値q 、センサで計測した外乱d 、および従来手法により決定した補正量c を含む生産データを収集する。 - (2)
- データ前処理
本稿では、生産設備の繰り返し動作区間をフレームと呼ぶ。収集したデータは時系列データのため、フレームの特定区間毎に平均値、最大値等の統計的な特徴量を算出し、対応する補正量c と紐付けてデータセットとする。特徴量演算部で用いる特徴量f の選択には、因果分析や重要度解析等を使用することができる。データセットの中から品質特性値q が品質特性基準値qr から大きく外れているデータを削除し学習/評価データに分割する。なお、品質特性基準値qr 、品質特性値q は以降の処理に使用しないためデータセットからは削除する。 - (3)
- 予測器の学習
特徴量f から補正量c を予測する回帰モデルを学習する。回帰には様々な手法があるが、本稿では高速に予測処理を実行可能な機械学習アルゴリズムである力学系学習木(Dynamics Learning Tree, DLT)4)を用いた。 - (4)
- 評価
評価データを用いて予測精度の評価を行い、予測モデルの性能評価を実施する。
以上の手順で構築した補正器を、図2のフィードフォワード制御系に用いることにより、外乱d の影響を打ち消す補正値c が適切に決定され外乱抑制制御が可能となる。
4. 実験
4.1 実験対象
本実験では、AIコントローラ上に本手法を実装し、放電精密加工研究所製サーボプレス機「ZENFormer nano」に接続して下死点位置制御によるプレス加工を行った。
「ZENFormer nano」は増力機構にボールねじを採用した4軸直動式サーボプレスとなっており、スライドを面でコントロールし、μ m単位での制御が可能となっている。図4に金型レイアウトを示す。サーボプレス機には、金型温度、製品厚等の各種状態を測定するセンサを取り付けている。順送加工により材料は左から右へと流れる。なお材料厚はロール交換時に事前に測定されているものとする。
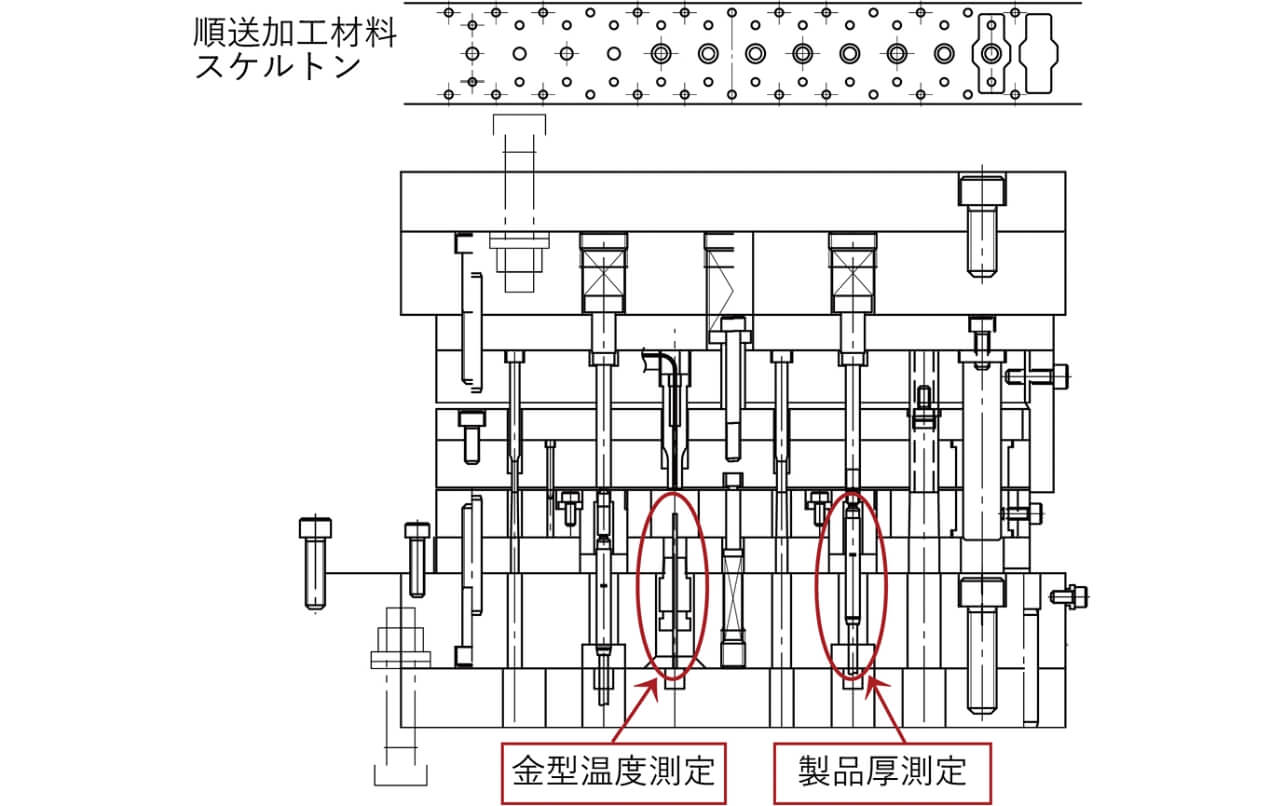
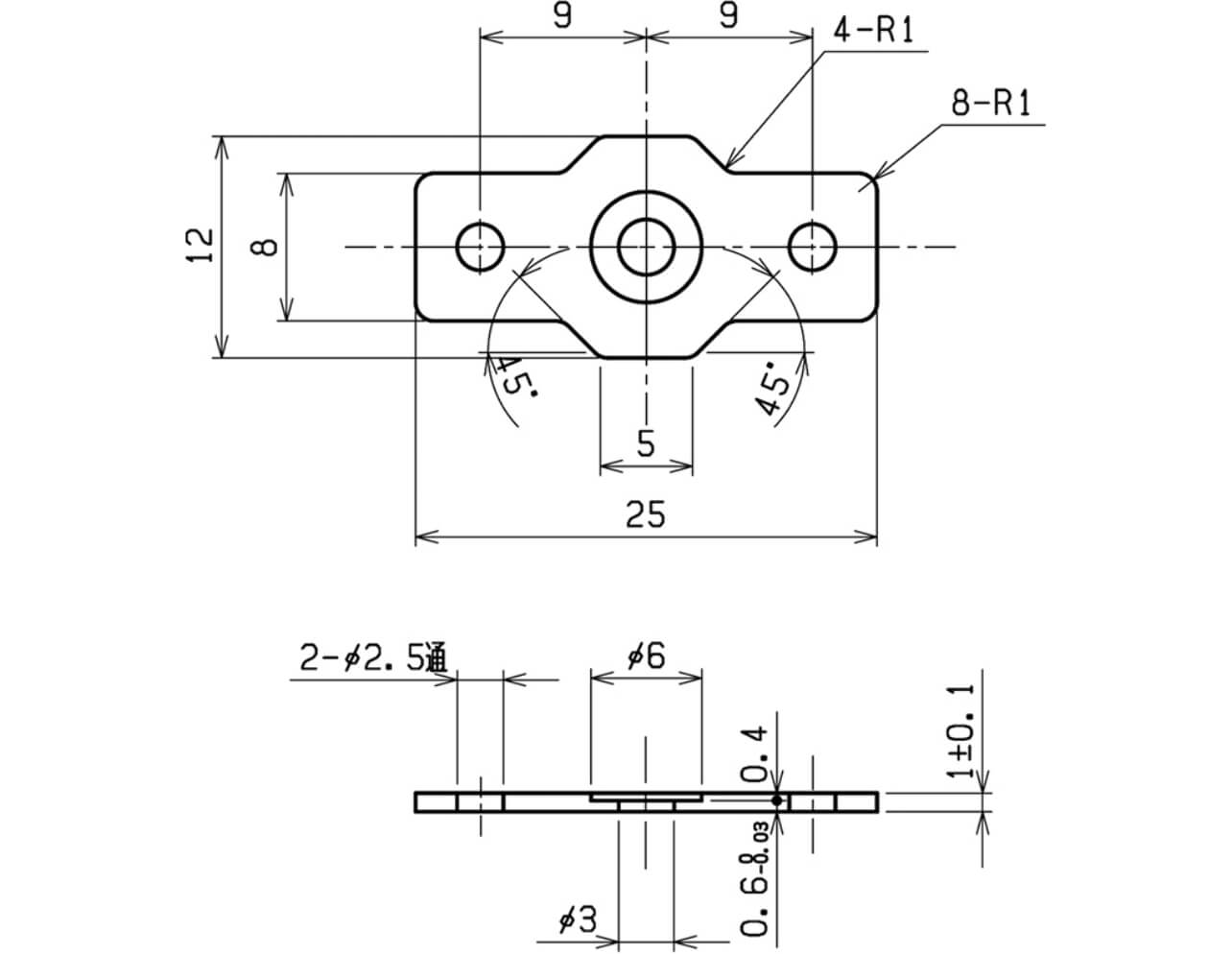
板厚1.00±0.05[mm]、幅32.0±0.20[mm]の一般的な冷間圧延鋼板であるSPCC-SDを使用して図5のフランジを製造し、中央のくぼみの厚さを0.6±0.01[mm]となるようにプレス加工する。
また、図1、2に示した制御系との対応および本実験において共通となる条件・設定値を表1に示す。
| 項目 | 対象 | 条件・設定値 |
|---|---|---|
| 品質特性基準値 qr |
目標製品厚 | 0.6±0.01[mm] |
| 品質特性値 q |
製品厚 | ― |
| 設定値 s |
下死点設定値 | 84.200[mm] |
| 補正量 c |
下死点補正量 | ― |
| 制御量 y |
スライダ位置 | ― |
| 外乱 d |
金型温度、材料厚 | ― |
| ― | 成形速度 | 30[mm/s] |
| ― | 下死点停止時間 | 500[ms] |
| ― | 実験開始時の周囲 温度 |
20~20.9[℃] |
4.2 補正量算出
本実験では図1の補正器の役割を人が担う(a)手動補正、(b)参考文献1)の手法を用いた自動補正、(c)提案手法を用いた自動補正による加工精度や誤差を比較する。
- (a)
- 手動補正(従来手法)
定期的に抜き取り、4箇所の製品厚をマイクロメータで計測し、4箇所の平均製品厚が0.6±0.003[mm]を超えた際に、作業者が下死点補正量を現在の補正量∓0.003[mm]に手動で設定する。 - (b)
- 自動補正(従来手法)
プログラムにより、連続する100ショットの製品厚の平均値と目標値の差分が±0.003[mm]を超えた際に、下死点補正量を現在の補正量∓0.003[mm]に自動で設定する。 - (c)
- 提案手法
金型温度と材料厚から特徴量f を演算し、予測器により下死点補正量を毎ショット算出する。なお金型温度は制御中の測定のためショット毎に変動するが、材料厚はロール毎の事前測定のためショット毎には変わらないものとする。
4.3 提案手法の補正器の構築
3.2補正器の構築手順に従い、(b)自動補正による生産データを収集し、補正器の構築を行う。本実験では収集した生産データのうち、製品厚が0.6±0.003[mm]以内のデータを学習データとして用いる。特徴量演算は外乱d の平均値を用いる。なお、補正器構築のための生産データは、実験結果に示すデータ以外にも複数の材料ロールで収集を行っている。学習データの範囲を表2に示す。
| 項目 | 学習データ |
|---|---|
| 材料厚[mm] | 0.9940~1.0182 |
| 金型温度[℃] | 19.2~26.5 |
4.4 実験結果
(a)手動補正、(b)自動補正、(c)提案手法をそれぞれ4000ショット行った実験結果について述べる。
- (1)
- 外乱傾向
各手法実験時の平均材料厚を表3に示す。材料ロールの厚さの規格は1.00±0.05[mm]である。各手法での実験毎に使用した材料ロールは異なるため平均材料厚も異なっている。
| 項目 | (a) 手動補正 | (b) 自動補正 | (c) 提案手法 |
|---|---|---|---|
| 平均材料厚 [mm] |
0.9996 | 0.9968 | 1.0061 |
図6に各手法実験時の金型温度の変化を示す。いずれも時間が経つにつれて温度が上昇する傾向がみられるが、実験日時の違い等の影響もあり、実験開始時の金型温度や温度上昇の仕方に違いがある。

- (2)
- 補正結果
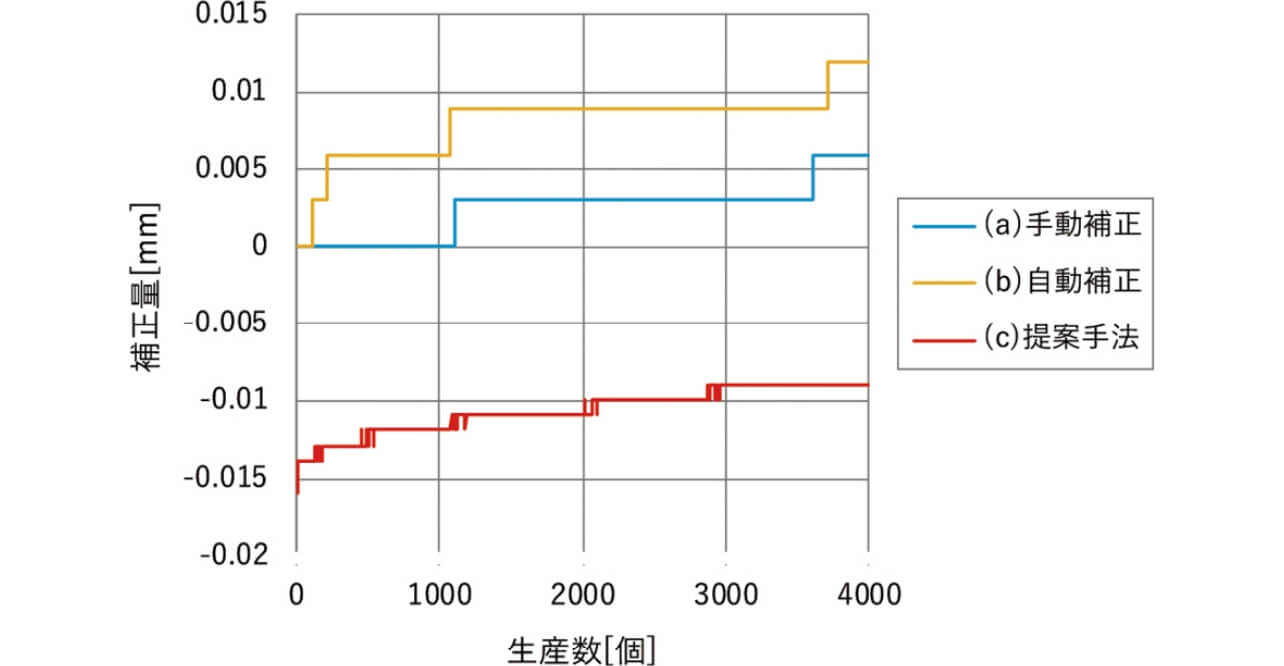
各補正手法を実行した結果の補正量を図7に示す。(a)手動補正、(b)自動補正に比べ、(c)提案手法では補正量が金型温度の変動に細かく追随できていることが分かる。各手法の下死点補正量の初期段階の違いは材料厚と金型温度が反映されている。(a)、(b)の従来手法ではフィードバックによる遅れのため、初期値は0であり適切な補正量に達するのに(c)提案手法よりも時間がかかっている。
- (3)
- 品質特性値の比較
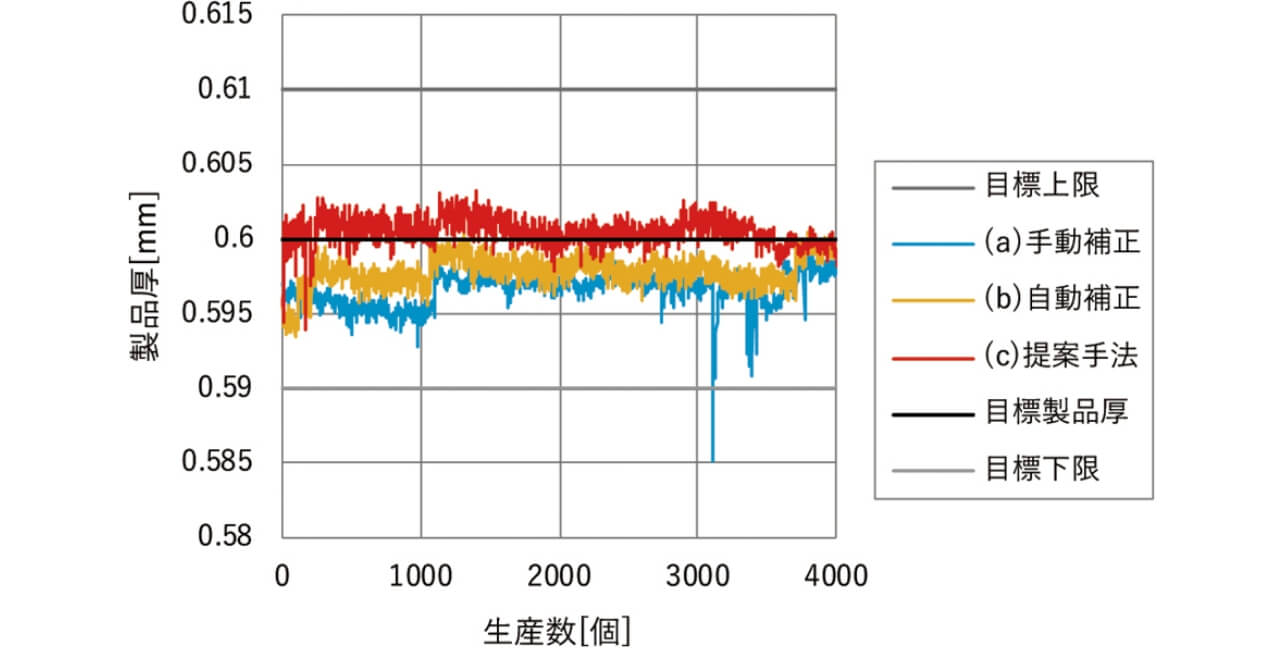
それぞれの下死点補正手法を適用し、品質特性値である製品厚を測定した結果を表4および図8に示し、以下で性能を比較考察する。
| 項目 | (a) 手動補正 | (b) 自動補正 | (c) 提案手法 |
|---|---|---|---|
| 平均[mm] | 0.5966 | 0.5978 | 0.6005 |
| 標準偏差 [mm] |
0.0012 | 0.0010 | 0.0008 |
| MSE[mm2] | 1.272×10-5 | 0.585×10-5 | 0.096×10-5 |
| 工程能力指数 (Cpk) |
1.89 | 2.56 | 3.75 |
- (a)
- 手動補正
工程能力指数は1.89と工程能力としては十分であるが、生産初期の製品厚が目標下限側にあり、少ない頻度での抜き取りによる補正のため、目標製品厚から偏った製品厚となった。目標下限値を超える突発的な製品厚の変動は材料厚や金型温度に極端に大きな変化がないことから、一時的なゴミの噛み込みや潤滑状態による影響が考えられる。 - (b)
- 自動補正
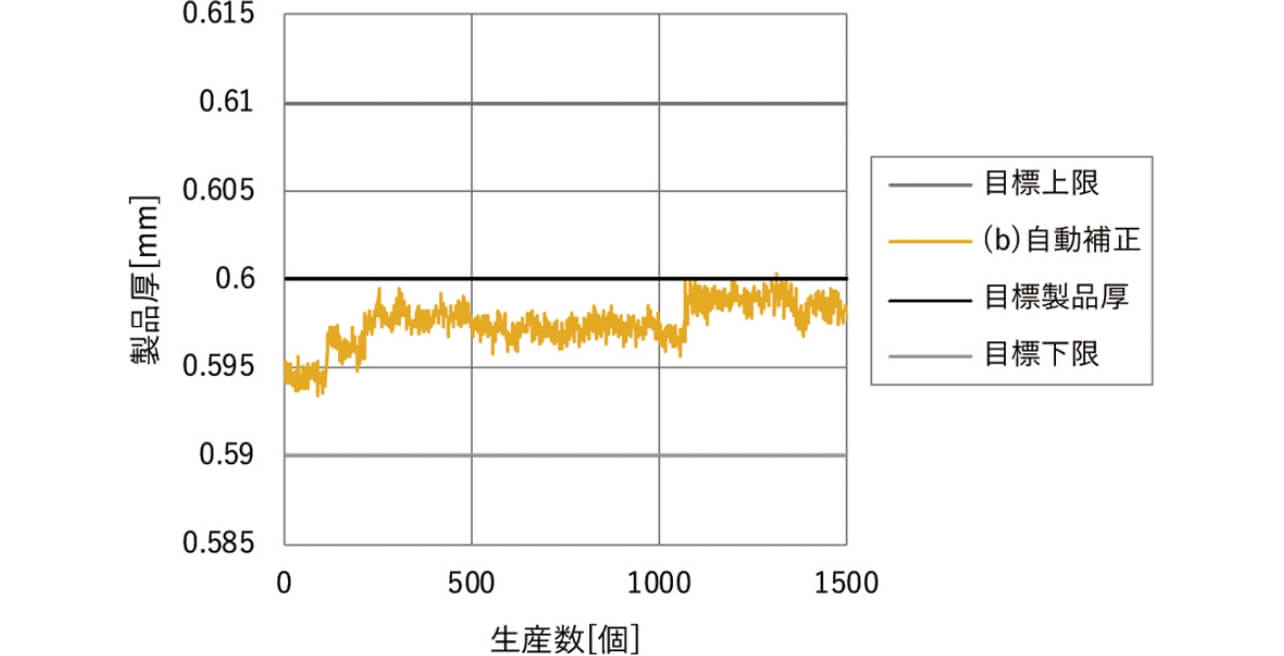
図9に実験開始時付近の製品厚を示す。(a)手動補正に比べ加工精度は高いが、同様に偏った製品厚となった。目標製品厚への収束に時間が掛かかっているのは、補正に製品厚100ショットの平均値を用いた補正量とする手法のためと考えられる。
- (c)
- 提案手法
(b)自動補正に比べ、平均製品厚は0.0017[mm]、製品厚のばらつきを示す標準偏差は0.0002[mm]改善している。また、生産開始時から目標製品厚中心に分布する結果となっており、金型温度や材料ロールの変更による影響を補正量に適切に反映していると考えられる。その結果、より目標製品厚0.6[mm]に近い製品厚とり、(b)自動補正に対しMSEは1/6に改善した。
5. むすび
本稿では、従来手法では十分に抑制できない外乱に対して、機械学習による補正量予測を用いた外乱補正手法を提案した。本手法をサーボプレス機下死点位置制御によるプレス加工に適用し、従来の自動補正に対してMSEが1/6となる加工精度の向上を確認した。
本手法では、機械学習を用いて使用環境により異なる2M変動の傾向に対しても適切な補正量を予測し、従来手法よりも高い精度で制御できることを示した。本実験では従来手法においても工程能力は十分であったが、本手法を適用することで、工程能力の不足している工程の改善効果が得られる。また、従来よりも寸法許容差の小さい高精度な製品を製造できるようになると考えられる。
本実験では材料厚と金型温度の2つの外乱のみを考慮したが、機械学習では一般に、変数が多くなると必要な学習データ量が増加することや、次元の呪いの問題等があり、予測モデルの構築が困難となる課題がある。そのため、今後はより多くの変動要因を持つ対象での実験も必要と考えられる。また、本手法の汎用性、安定性、安全性についても今後、シミュレーションや別の対象への実装による評価を通じて検証を行っていく。
謝辞
実験にご協力頂いた、株式会社 放電精密加工研究所 産業機械事業部の皆様に感謝申し上げます。
参考文献
- 1)
- 村田力.プレスおよび金型におけるセンシング技術―サーボプレス・金型から見えるプレス加工のメカニズム―.素形材.2017, Vol.58, No.9, p.17-23.
- 2)
- 藤井高史,上山勇樹,阿部泰明.反復学習制御によるサーボプレス機の下死点補正の一検討.平成30年電気学会産業応用部門大会講演論文集.2018-08-28, p.19-22.
- 3)
- 見置孝昌,出来仁太郎.AI搭載マシンオートメーションコントローラの開発(1).OMRON TECHNICS.2019, Vol.51, No.1, p.39-44.
- 4)
- 沼倉彬雄,加藤成将,佐藤和幸,富沢武弥,三好扶,明石卓也,金天海.力学系学習木―連続力学系の階層型学習.情報処理学会第77回全国大会.Vol.2015, No.1, p.993-994.
本文に掲載の商品の名称は、各社が商標としている場合があります。














