歩行軌道のAI予測技術を適用した製造現場でのロボット衝突回避技術
- 機械学習
- 人歩行軌道予測
- 協調生産システム
- 協働ロボット
- ロボット軌道計画
近年、製造現場において人とロボットが同じ空間で作業することを実現するために、人との衝突を安全に回避するロボットの軌道計画技術開発が複数の研究機関や製造業等で進んでいる。しかし従来の技術は、ロボットが回避動作を実施する前に作業動作を一旦停止しなければならないため、人と密接する際にロボットが頻繁に停止し、生産性が著しく低下する問題がある。
本研究では、この問題を解決するために必要な技術の1つとして、製造現場における人の数秒先の体幹位置の予測技術に取り組んでいる。
今回、従来のAIによる歩行軌道の予測技術を製造現場での人体幹位置予測に適用する手法を考案し、製造現場の1事例を用いて性能評価を行った。その結果、4s先の体幹位置の予測を0.4msの処理時間で実現でき、現段階の技術課題も判明した。また、比較評価実験により、本手法はオーソドックスな時系列解析手法より予測精度が優れており、処理速度が10倍以上速いことが分かった。
1. まえがき
近年、製造業において技能人材確保が深刻になってきた1)。この課題を解決するために、人手作業の製造現場の一部をロボットで置き換え、従来の人とロボットを隔離していた安全柵を撤廃し、人とロボットが共存しながら作業を行う生産方式が注目されている。
産業用ロボットを導入する際の安全確保の手段としては、一般的に安全柵や安全センサを用いて人とロボットを隔離する手段と、人と衝突しても人に怪我をさせないPFL(Power and Force Limiting)協働ロボットを採用するという二つの手段がある2)。前者は、柵や安全設備でロボット専用の作業スペースを確保するため、スペース効率が低下したり、フレキシブルなレイアウト変更が困難となったりする課題がある。後者は、柵レスで人と共存できるが、ロボットの速度と動力が常に制限され、稼働中に人との衝突によりロボットの動作停止が頻繁に発生するなど、産業ロボットの本来の生産性が発揮できない課題がある。
上記課題を解決するために、近年は、センサにより人の動きを検出し、ロボットが人の動きに合わせて、人と衝突しないように動作軌道計画を行う技術が注目されている3)4)。これにより、柵レスで人と共存する際に、衝突によるロボットの停止が低減できると考えられている。
この技術に関するほとんどの研究は、人の動きをリアルタイムに検出し、その情報に基づいて人とロボットの位置関係を監視する手段をとっている。この手段によると、人とロボットは事前に設定された、人の安全確保に必要な距離以上に近づく場合、つまり、過接近の場合、ロボットの動作を停止させて、必要な距離を確保できる新軌道を生成してロボットの動作を再開する。
一方、この方策においては、人とロボットの過接近が検知された時に、新軌道がまだ決まっていないため、ロボットが衝突防止のために実行中の動作を停止しなければならない。従って、狭い作業空間にロボットが人と密接して作業する場合、過接近が頻繁に発生するため、ロボットの作業が頻繁に中断されるという問題がある。
上記の問題を解決するための必要な技術の1つとして、製造現場における人の動きを予測する技術に取り組んだ。この技術により、直近将来の人位置情報の取得ができ、人とロボットの相対位置関係の予測が可能になる。そのため、過接近が実際に発生する前に新軌道生成を完了することが可能になり、ロボットが停止せずに新軌道に切り替わるようになる。これにより、従来の衝突回避動作の停止問題が低減され、ロボットがスムーズに人との衝突を回避することが実現できる。
なお、本研究では、製造現場においてロボット近傍で作業を行う人の動きを、①各作業場所間での体幹の移動と、②止まって手作業する際の手の動きの2つのステップに分ける。現段階は、上述①の人の体幹位置の予測を取り組んでいる。
人の歩行による体幹位置の変化、つまり歩行軌道は、環境や個人差など多くの影響を受け、理論計算で導くことが非常に難しいため、近年は人工知能(AI)を用いた予測技術の開発が進んでいる。
従来技術は、混雑した空間における複数人の歩行軌道を、画像データを用いて予測するといった用途で使用されており、数秒後の人位置の予測が実現できている5)6)。ニューラルネットワークを使ったアルゴリズムにより、大量な学習データを用いるため、予測の処理時間が数秒かかっており、また、予測距離誤差が約1mである。
一方、これらの技術は、自動車の自動運転用途など、オープンな空間での歩行軌道予測のために適用されているが、製造現場の閉鎖的な空間への適用に関する研究はまだ進んでいない。また、予測処理に時間がかかりすぎるため、ロボットの動作に合わせたリアルタイムな処理ができない課題がある。
本研究は、前述したスムーズな衝突回避を実現するために、従来のAIによる歩行軌道の予測技術を製造現場での人体幹位置予測に適用する手法とその効果を検討した。検討に際しては、まず必要な予測性能指標と目標値を定義し、それらを達成するために、従来技術を製造現場に適用するためのアプローチを考案し、それをベースに具体的な適用手法を提案した。また、製造現場の1事例を用いて適用手法の効果と課題を検証した。これらの内容について、本論文で紹介する。
人とロボットが協働作業するための技術なので、安全化設計も重要なポイントとなるが、本論文では、AIによる予測技術に焦点を当てているため、安全化の仕組みについての説明は割愛する。実際には、安全関連部とAIによる人予測アルゴリズムを別系統で構成することにより安全性は実現できていることのみ、ここでは述べておく。
2. 予測性能指標と目標値
前述の人と密接する際にロボットの作業が頻繁に中断される問題を解決するための、人の位置予測によりスムーズに衝突回避を行う概念を、図1に具体化した。このフローにおいて、数秒後の人位置を予測し(a)、その情報を用いて将来の人とロボットの位置関係を計算し、過接近が発生しそうかを判断する(b)。YESの場合に衝突を回避するようにロボットを制御する(cとd)。
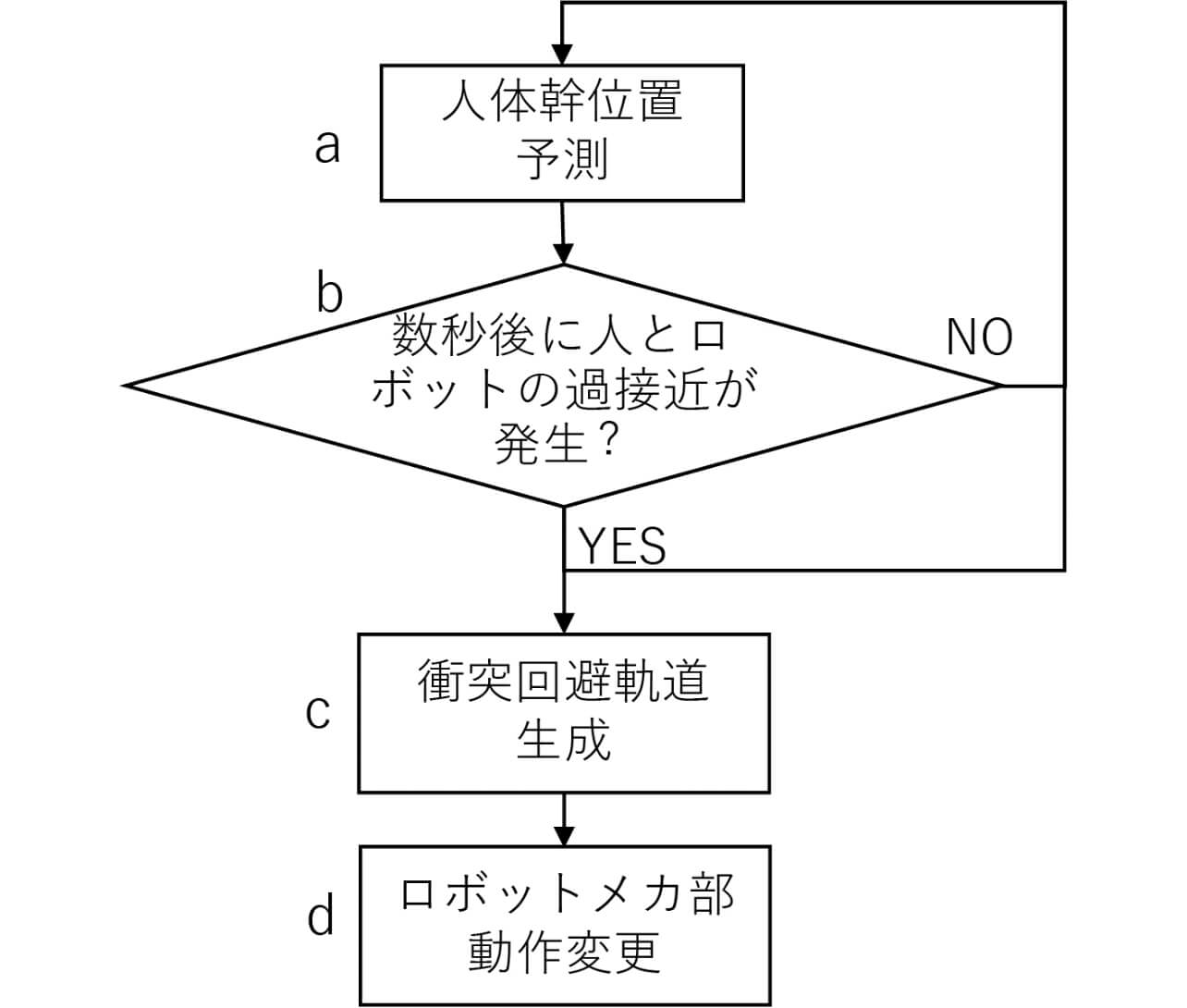
稼働中に人の安全を確保するために過接近の判断を常に行わなければならないため、aとbは短周期で連続的に実行される必要がある。また、スムーズな衝突回避を実現するために、過接近が実際に発生する前に、つまり、人体幹位置予測(a)の予測時間内にa~dの処理が全部終わることが重要なポイントである。
従って、このフローを実現する上で、図1の処理フローの(a)人体幹位置予測の性能が重要となる。この性能を表す指標として、「予測処理時間」「予測可能時間」「予測距離誤差」を定め、それぞれの目標値を以下のように定義した。
- 予測処理時間
1回の予測処理の所要時間である。前述の短周期で連続的に実行することのために、この指標を極力短縮させる必要がある。
本研究では、オムロン製レーザスキャナ(形OS32C)により、予測に必要なデータを40ms周期で取得する(2.3節で詳細を説明する)。それと連動して予測処理を連続的に行うために、予測処理の処理時間目標を40ms以下と設定した。 - 予測可能時間
予測処理により予測が可能な直近将来の時間である。前述のように、この指標の目標値は、図1のa~dの処理の所要時間により設定するべきである。本研究では、システムの構成により、a~dの処理時間を表1に記載するように見積もった。これらの値は、実装ハードウェアの性能により変動する可能性があるが、研究段階は厳密な評価を省略し、厳しめに設定した。
これらの所要時間の合計にデータ伝送などのバッファー時間を加えて、予測可能時間の目標を1.2sに設定した。 - 予測距離誤差
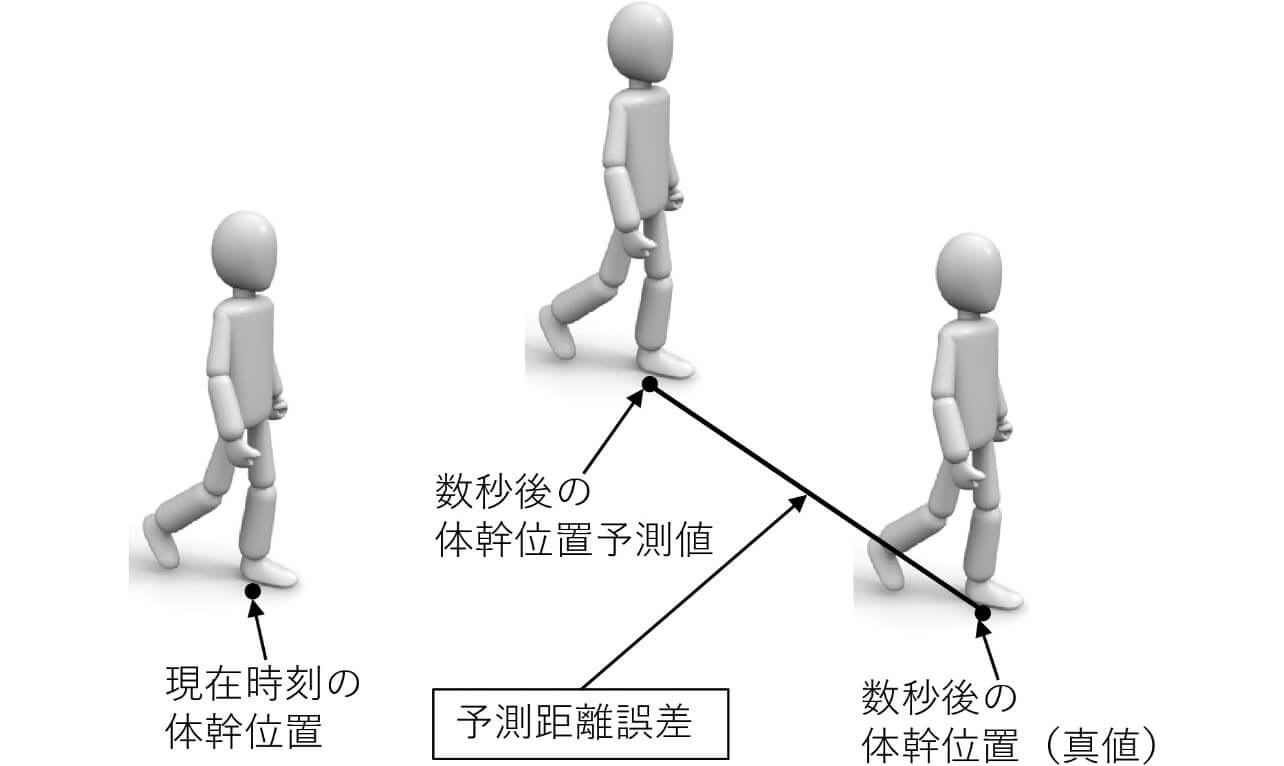
人体幹位置の予測値と真値の距離である(図2)。体幹位置は、体幹中心点の位置で示す。これについて3章で説明する。この指標は、予測結果の正しさを示し、前記フローのbで予測結果を用いて過接近を判断する際に、予測アルゴリズムによる誤差として考慮されるべきである。
本研究では、事前机上計算により、“密接”とみられており、ロボット第1関節回転軸を中心とした2メートル半径の円柱領域内に人が作業する場合、スムーズな衝突回避を実現するために100mm以下の予測距離誤差内であれば効果が得られるという結果を得ている。このため、目標値を100mm以下と設定した。
| 図1での番号 | 処理時間[ms] | 処理時間の決め方 |
|---|---|---|
| a | 40 | 予測処理時間の目標値(2章)により設定した |
| b | 10 | 汎用PCで過接近判断処理のプログラムを実行した際の実績数値を参考に設定した |
| c | 100 | 専用処理ハードウェアでProbabilistic roadmap法による6関節ロボットの軌道計画処理3)の所要時間実績数値を参考に設定した |
| d | 800 | オムロン製協働ロボット(TM5シリーズ)の加減速性能により設定した |
3. 製造現場適用のためのアプローチ
AIを歩行軌道の予測技術に使用する際に、一般的な使い方としては、歩行軌道の変化に影響する個人・環境因子を特徴量とし、それらが含まれる学習データを使って、特徴量による歩行軌道の変化に関する法則性を学習器に学習させる。学習済の学習器を用いて、同様な特徴量が含まれる予測のためのインプットデータを解析することにより、歩行軌道の変化を算出する。
従来のAIによる歩行軌道の予測技術は、複雑な環境における複数の歩行軌道に着目し、正確な予測結果を得るために、障害物の位置や同行する人数など多くの特徴量を考慮する。予測時に、それらが含まれる大量のインプットデータを解析するため、数秒の予測処理時間がかかる。このため、前章で定義した予測処理時間の目標値である40msに対しては大きなギャップがあり、そのままのアルゴリズムでは適用できない。
この問題に対して、本研究では、特徴量の数を最小限にすることにより、予測処理時間を短縮させるようにした。
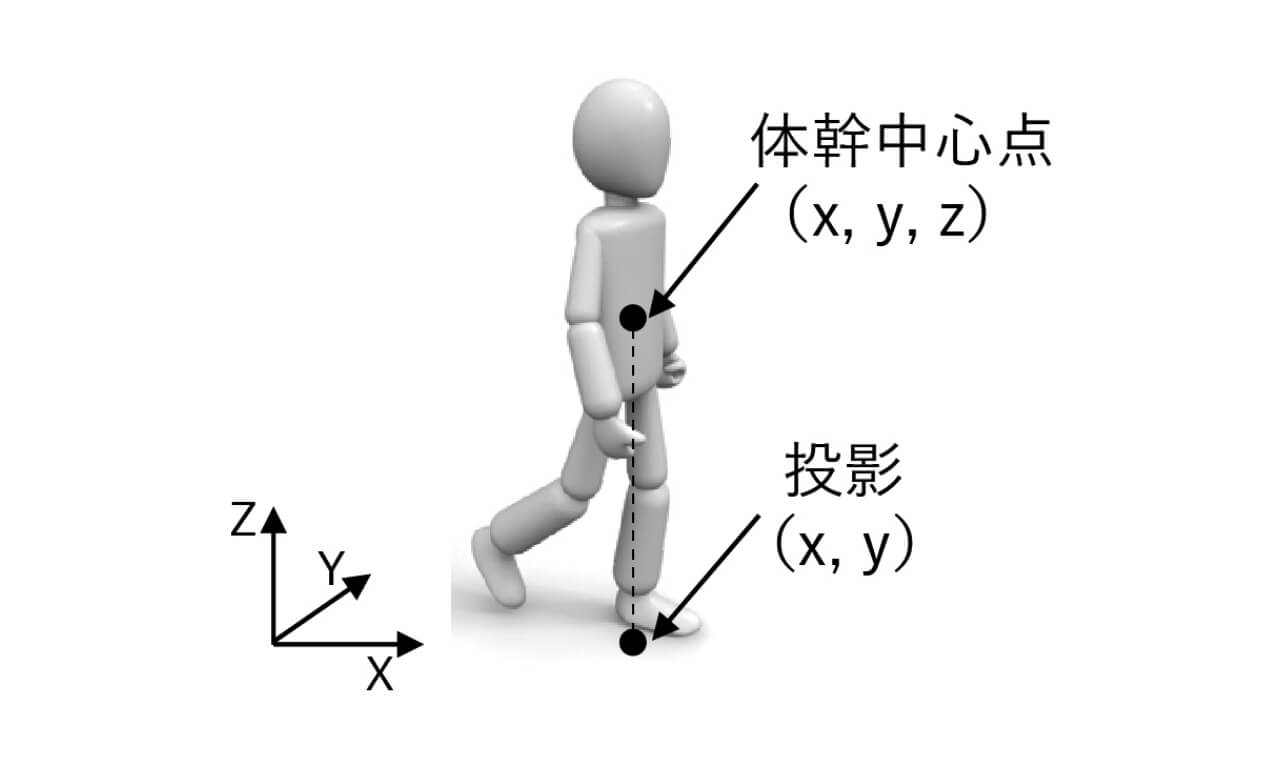
具体的には、本研究の予測対象となる製造現場における人は、ほとんどの場合は平らな地面で歩行し、高さ方向上の位置変化が微小のため、体幹の位置は体幹中心点の投影、つまり、体幹中心点の座標値(x,y)により表すことが可能となる(図3)。従って、体幹中心座標(x,y)を歩行軌道の予測に最低限必要な特徴量として使用することにした。手作業の時間のばらつきなどの因子を特徴量に加えたら歩行軌道の予測精度がさらに良くなる可能性があるが、予測処理時間とはトレードオフの関係になるため、予測処理時間優先で今回は考慮から外した。今後、さらなる改善にこの特徴量が必要であれば、次のステップにおいて検討する予定である。
4. 予測手法の詳細
4.1 概要
前述した学習特徴量の数を最小限にするアプローチをベースに、AIによる歩行軌道の予測技術を製造現場における人の体幹位置予測に応用する手法を提案した。手法の概要を下記観点で説明する。
- 特徴量
3章で記載するように、人の体幹中心座標のxとyを特徴量とする。
- 学習データ
体幹中心座標の時系列データを学習データとする。これらにより学習器に体幹中心座標変化の法則性を学習させる。
- 学習器
力学系学習木手法7)に基づくDeep Binary Tree(DBT)学習器(株式会社エイシング製の機械学習パッケージ)を学習処理部として採用した。
DBTは、少量データによる高速な学習処理が得意であり、計算量が小さく組み込みシステム上でも利用しやすいことなどの特徴がある。本研究においても学習データは少ないので、最終的にロボットシステムに組み込みやすく、かつ高速処理が可能なDBTを採用した。 - 予測アルゴリズム
製造工程を繰り返す人の体幹中心座標の時系列データをリアルタイムに取得し、それを上記学習データにより事前に学習済の学習機に入力することで、直近将来の体幹中心座標値を出力データとして取得する。
また、教師ありのAI技術の特徴として、予測用の入力データが有効であるほど正確な予測が可能のため、学習器事前学習の段階で、入力データの形式に関するパラメータのチューニングを行い、予測距離誤差の改善を図る。 - システム構成
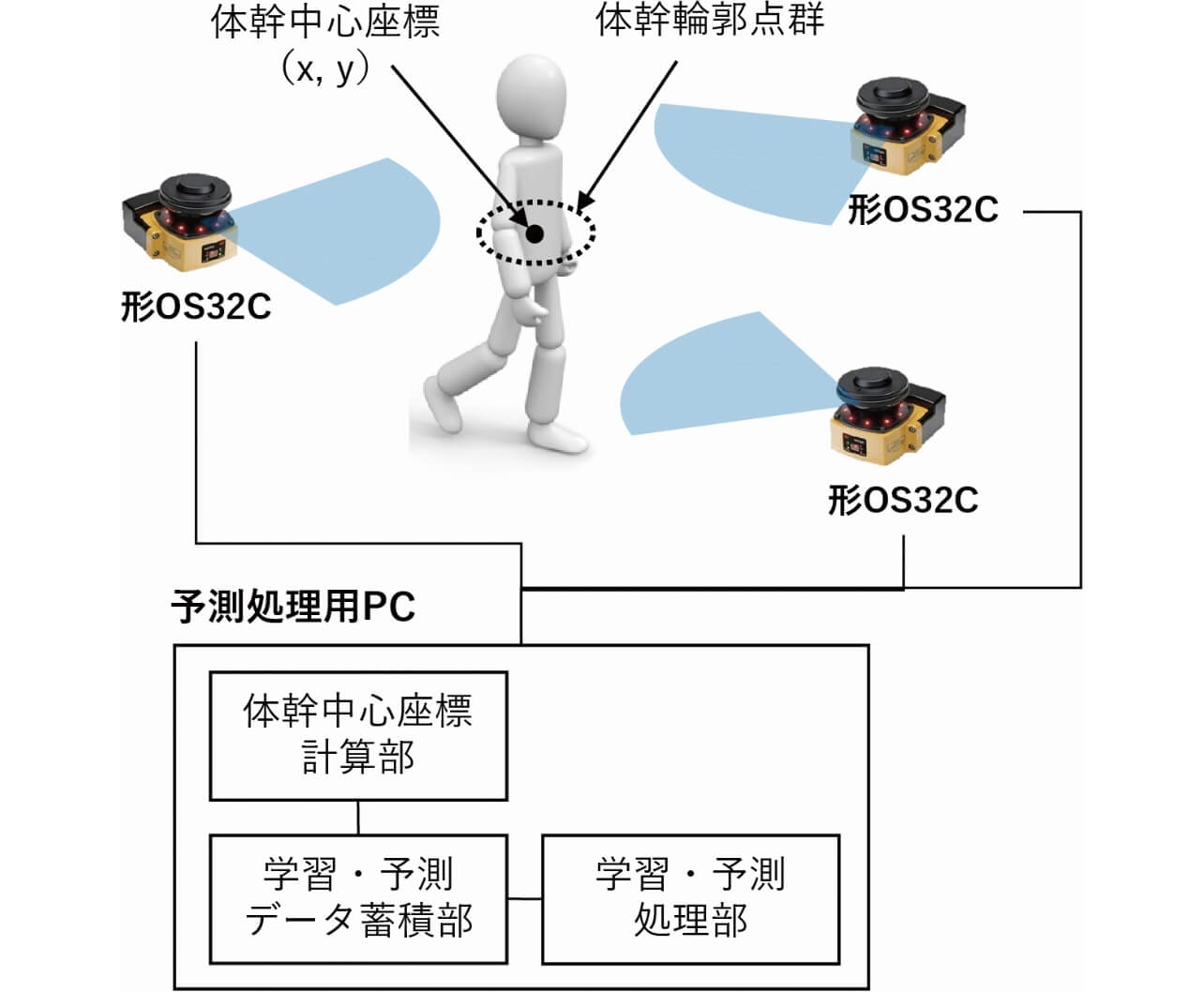
図4に示すように、本研究では、3台のレーザスキャナ(形OS32C)が人の腰と同じ高さに配置され、腰周りの体幹輪郭点群の座標値を40ms周期で連続的に検出する。検出データが周期ごとに予測アルゴリズムが実装された予測処理用PCに送信され、点群の中心点の座標値xとy計算し、それを点群が検出された時刻の体幹中心座標値とする。この方法で取得された体幹中心座標値の時系列データが学習・予測データ蓄積部に蓄積されて、処理部で解析される。
4.2 詳細アルゴリズム
本研究で提案した適用手法のアルゴリズムに関して、処理フローを用いて詳細を説明する。図5に示すように、本手法の処理フローはA~Cの三つのセクションで構成される。
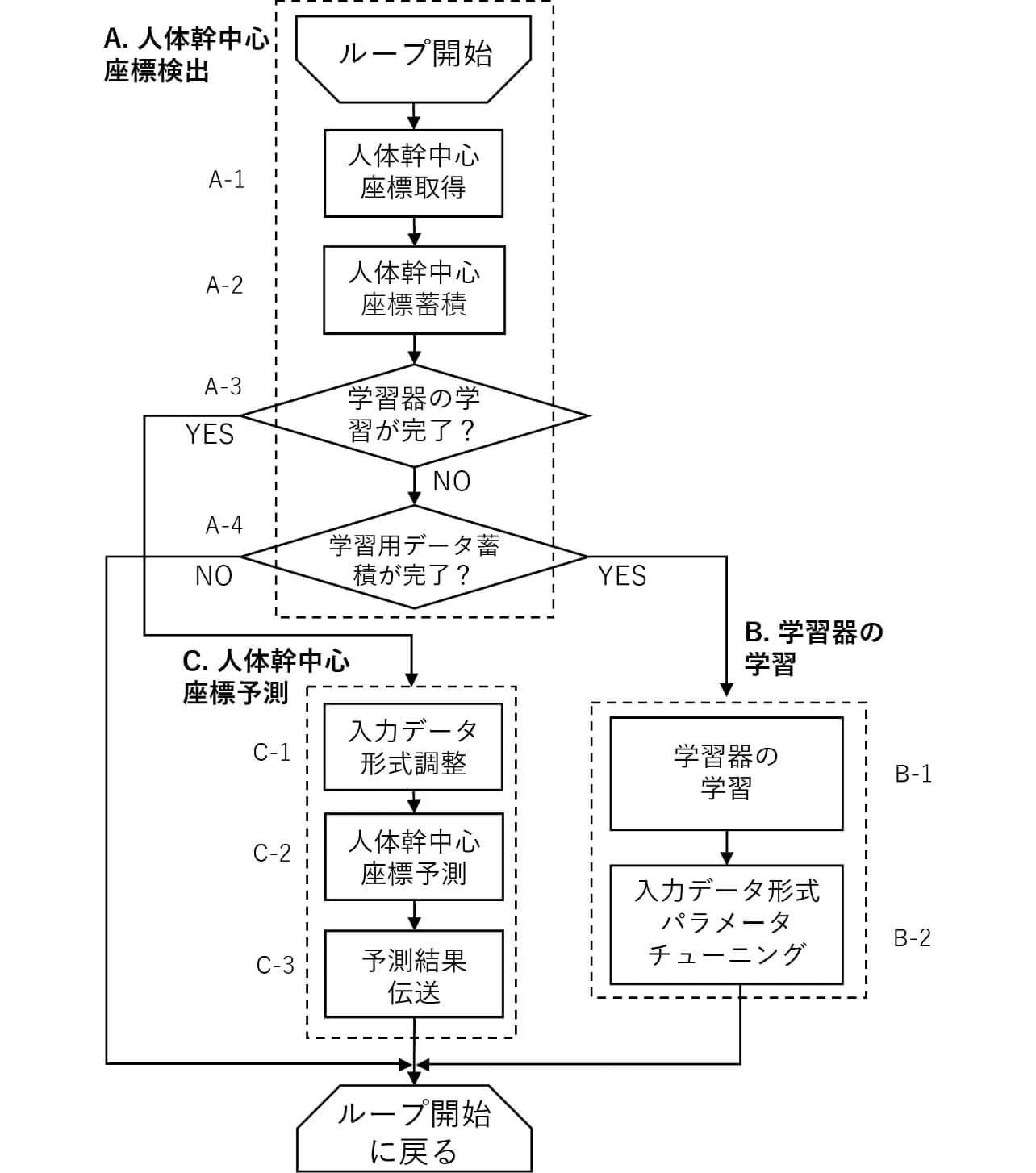
セクションA(人体幹中心座標検出)
本セクションは、前述(4.1節)のシステム構成で記載したように、体幹中心座標値(x, y)を取得し、蓄積する。
セクションB(学習器の学習)
本セクションは、セクションAで蓄積された人体幹中心座標データにより、DBT学習器を体幹中心座標変化の法則性、つまり過去体幹位置と将来体幹位置との関連性を学習させる。また、より正確な予測結果を得るように入力データの形式に関するパラメータをチューニングする。
本セクションの処理は、図6を用いて説明する。図の体幹中心座標値(x,y)の記号はその座標値が取得される時刻を示す。例えば、(

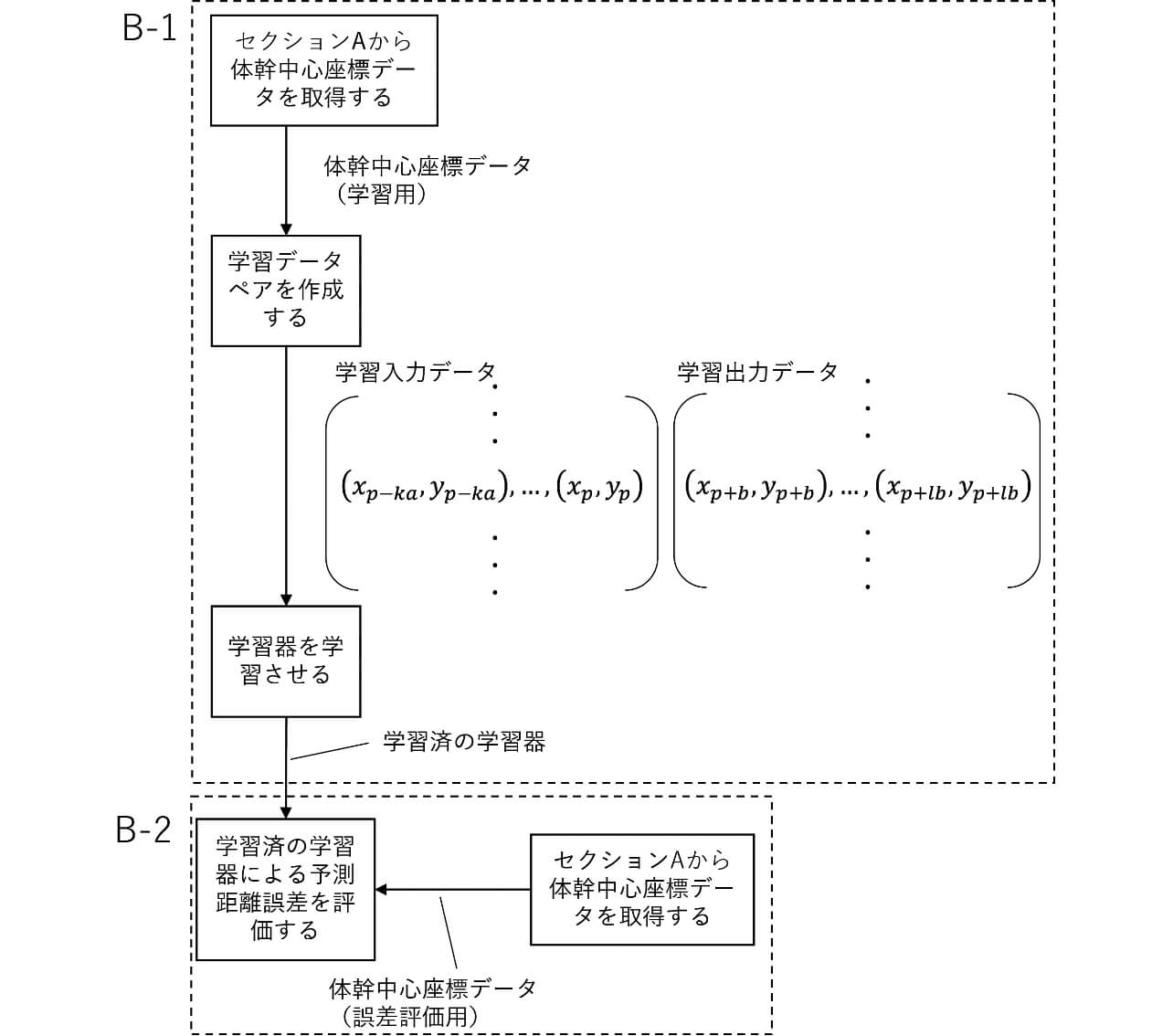
まず、学習器に過去体幹位置と将来体幹位置との関連性を学習させる。具体的には、図6のB-1に示すように、セクションAで蓄積されたデータの一部を学習用のデータとして取得する。データ取得された時刻(図の例は時刻p )ごとに、以前に取得されたデータを学習入力データとし、以降に取得されたデータを学習出力データとして抽出し、データペアを作成する。これらの学習データペアを学習器に学習させる。ここでは、入力データの形式は、データの数(k )とデータ間の時間間隔(a )で決められ、後述するようにチューニングされる。出力データの数(l )と時間間隔(b )はチューニングせず、予測要件に応じて設定する。
次に、図6のB-2部分に示すように、セクションAで蓄積されたデータの一部を誤差評価用データとして取得し、B-1で学習済の学習器により体幹位置を予測する場合の予測距離誤差を評価する。評価方法に関しては5.2節で説明する。
また、入力データ形式パラメータのk とa に対して一定の範囲内でグリッドサーチを行い、図6の学習(B-1)と評価(B-2)を繰り返すことで、最小の予測距離誤差を得られるk とa の値を見つける。
セクションC(人体幹中心座標予測)
本セクションは、セクションBにより取得した学習済の学習器と、k とa の値を用いて、直近将来の人体幹中心座標を予測する。
以下に、処理の詳細を図7により説明する。
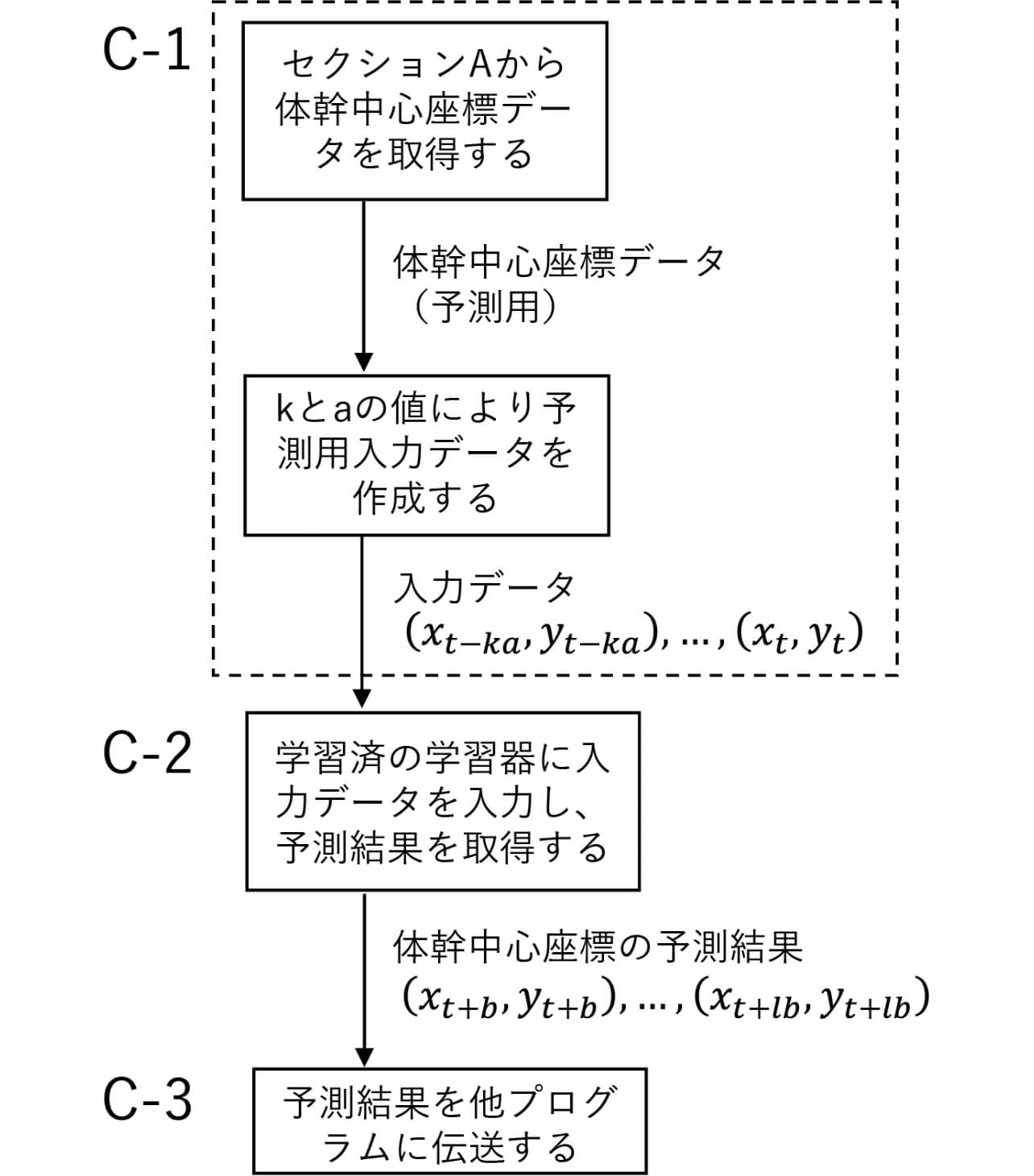
セクションAから現在時刻(図の例は時刻t )までの体幹中心座標の時系列データを取得し、セクションBで決められたk とa の値を用いて予測用の入力データを作成する。これを学習済の学習器に入力し、直近将来(図の例は、l ×b 秒先)の体幹中心座標を取得する。
この予測結果を用いて、直近将来のロボット位置情報を加えたら、前述の回避処理フロー(図1)のブロックbで人とロボットの直近将来の位置関係が推測でき、過接近が発生するか判断が可能になる。
5. 性能評価
本章では、製造現場の1事例としてU字型製造ラインを模擬した実験環境において、前述のAIによる歩行軌道予測技術の適用手法を予測可能時間、予測処理時間、予測距離誤差の観点で評価した結果を説明する。
5.1節で実験の条件、5.2節で評価方法、5.3節で実験の結果と考察を説明する。
5.1 実験条件
実験環境セットアップ
当社工場の小型電子部品組立用のU字型製造ラインを参考にして実験環境のレイアウトを設計した。図8にこのレイアウトの鳥瞰図を示す。図8に示すように、U字型に設置される作業台により囲まれ、ドットで示してあるエリアにおいて、人が作業のために歩行で移動する。
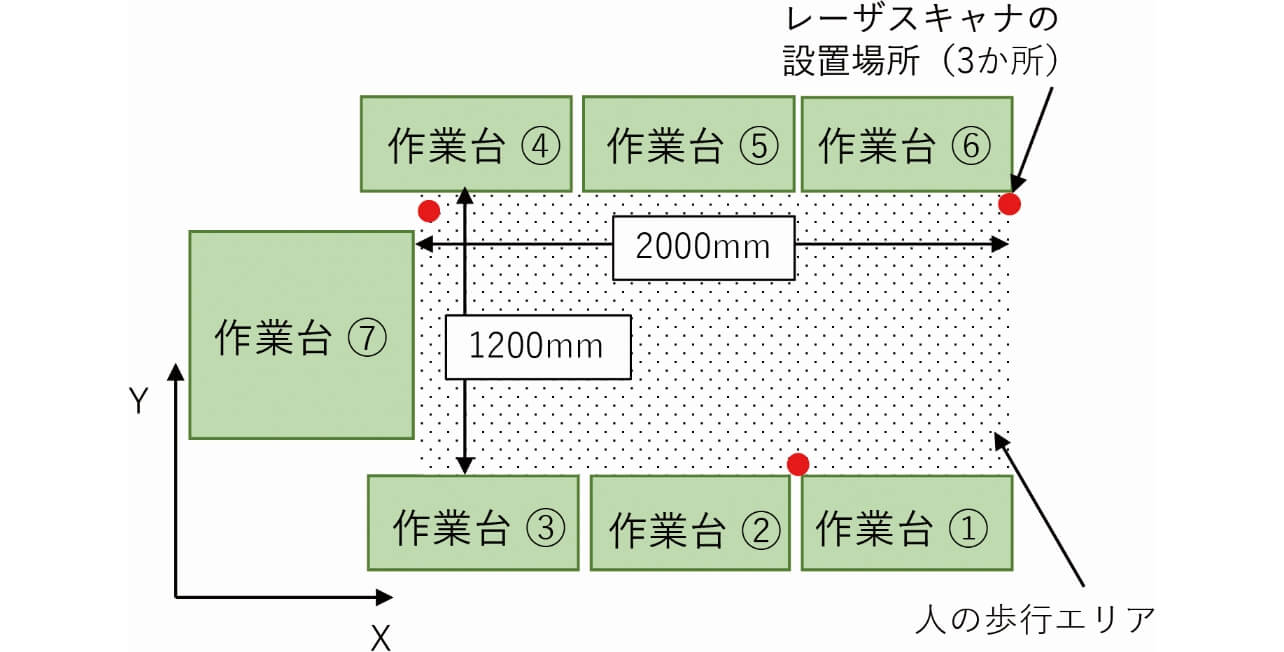
歩行エリアを全部カバーできるように、体幹輪郭検出用のレーザスキャナが3か所に設置される。
人体幹中心の座標系については、作業台①~③の並び方向をX軸、その垂直方向をY軸と設定した。
実験用の歩行軌道
当社工場のU字型製造ラインにおいて、小型電子部品組立作業を行う作業員の歩行軌道に基づき、以下の4つの実験用歩行軌道の構成インデックスを抽出した。また、複数の作業工程を調査した結果により、それぞれの代表的な値を決めた。
- 軌道形状
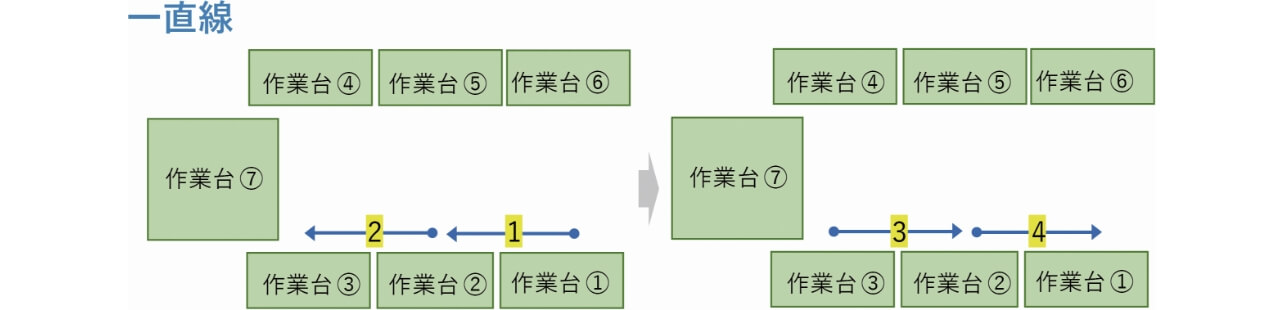
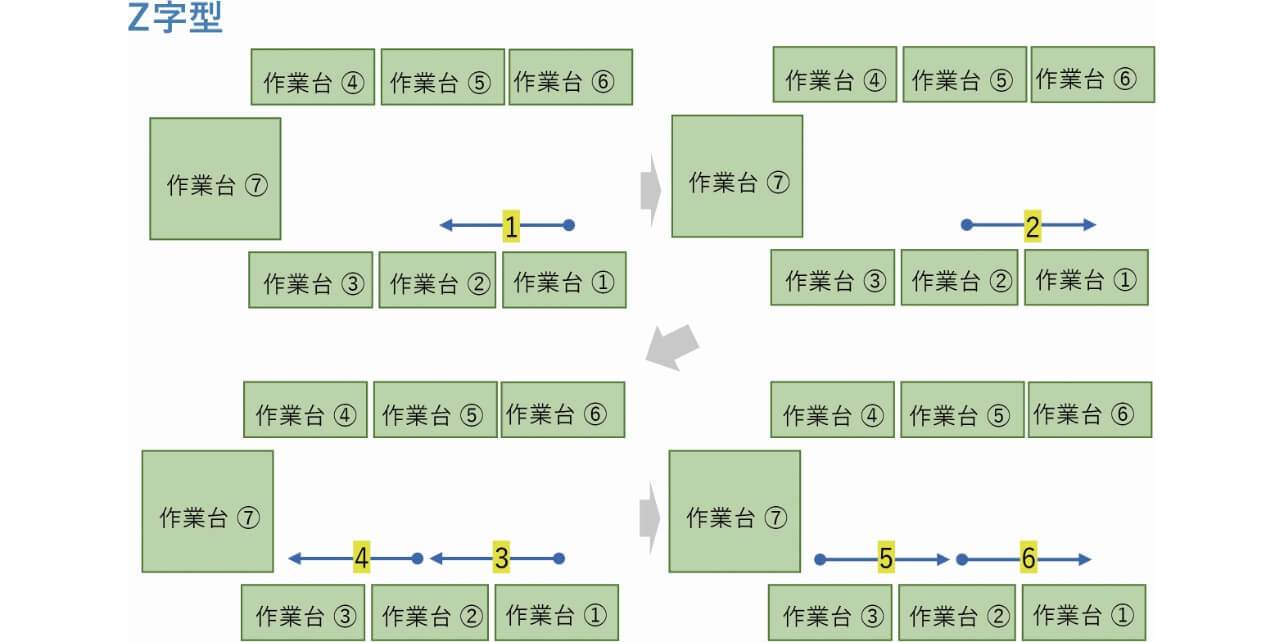
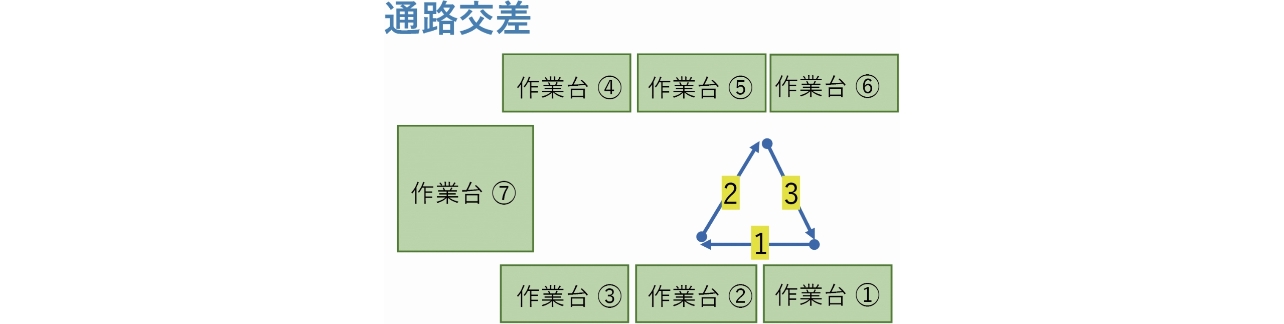
歩行軌道の形状である。本実験では、1直線、Z字型、通路交差の3つの形状を定義した(図9~図11)。図の中の、矢印線は人の移動を示し、丸点が始点、矢印が終点である。線の番号は移動の順番を示す。
- 速度
人移動時の歩行速度である。本実験では、低速(約1000mm/s)と高速(1600mm/s)の2段に設定した。高速の速度値は、人ロボット協調安全規格(ISO10218-1/TS15066)で指定された値を使用した。
- 移動距離
移動の距離、つまり図9~図11の矢印線の長さである。本実験では、600mmと1200mmの2種類に設定した。
- 停止時間
作業台で手作業のために、移動の停止時間、つまり図9~図11の矢印線の間の停止時間である。本実験では、2sと10sの2種類に設定した。
上記インデックスの組み合わせで、6種類の歩行軌道を設定した(表2)。現場で一番多く見受けられる#1を標準パターンとし、#2~#6は#1をベースとしながら、1つだけのインデックスを変化させるように設定した。この設定によって、個別の軌道インデックスと予測結果の関連性を評価できると考えた。
| # | 軌道形状 | 速度 [mm/s] |
移動距離[mm] | 停止時間[s] | 学習用データ数 | 評価用データ数 |
|---|---|---|---|---|---|---|
| 1 | 1直線 | 約1000 | 600 | 2 | 9102 | 4551 |
| 2 | Z字型 | 約1000 | 600 | 2 | 8663 | 4332 |
| 3 | 通路交差 | 約1000 | 600 | 2 | 9207 | 4603 |
| 4 | 1直線 | 約1600 | 600 | 2 | 6332 | 3166 |
| 5 | 1直線 | 約1000 | 1200 | 2 | 4477 | 2239 |
| 6 | 1直線 | 約1000 | 600 | 10 | 9637 | 4818 |
予測処理に関するパラメータの設定
- 入力データ形式に関するパラメータ(k とa )のチューニング範囲
本実験では、k は[1,100]の範囲に1刻みで、a は[0.04s,4s]の範囲に0.04s刻みでチューニングした。 - 出力データの形式( l とb )の設定
本実験では、予測出力データの数(l )を30、50、100の3パターンに、データ間の時間間隔(b )を0.04sに設定した。l とb の組合せにより、予測可能時間(l xb )を1.2s、2s、4sとした。
5.2 評価方法
前記の実験環境において、1人の作業員が前記の実験用歩行軌道に沿って、各軌道の移動を30回繰り返す。その間に、前述の予測システム(図4)により、作業員の体幹中心座標値データを取得し、30回の内の20回のデータを学習用データとして用い、学習器を学習させる。残りの10回のデータを評価用データとして用いて、各軌道に対して、1.2s、2s、4s先の体幹中心座標値を予測し、以下の方法で、予測性能指標を評価した。各軌道の学習・評価用データの数は表2に示す。
- 予測処理時間の評価方法
実験する際に、本技術の予測処理の部分(図5のセクションC)の所要時間をループごとに計測する。この時間の最大値を予測処理時間とする。
- 予測距離誤差の評価方法
各軌道に対して、体幹中心座標が取得される時刻ごとに、実測座標値と予測座標値の相対距離を算出し、最大値を予測距離誤差とする。本実験では、距離分布の「平均値+3σ」を最大値とする。
レーザスキャナの計測距離ばらつきによる影響が大きく、センサの計測ばらつきを扱うのに一般的に3σで評価することから、「予測距離誤差」に関しては3σで評価している。
5.3 実験結果
3.1節、3.2節に記載した方法に従い、評価実験を行った結果を表3にまとめる。
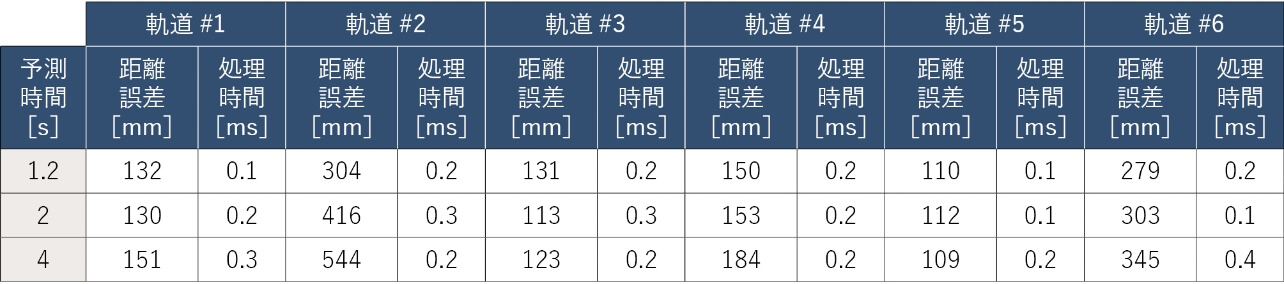
予測距離誤差について、予測時間が長いほど誤差が大きくなる場合が多く、1.2s先予測の場合の最大誤差が304mmとなり、本研究の目標値に対しては乖離がある。4s先まで予測する場合の最大誤差が544mmとなり、軌道#2で発生したことを確認できた。
予測処理時間について、全ての実験ケースでの処理時間が1ms以下になり、最大値が0.4msであることを確認できた。目標の40msをクリアし、本研究の予測システム構成で40ms周期の連続予測処理が可能であることが分かった。
今後の改善のために、実験データを用いて誤差に対する影響因子を追究した。表4に各軌道の1サイクルあたりの停止回数と合計停止時間を示す。比較的大きな誤差が現れる軌道として、軌道#2は1サイクルあたりの停止回数が多く、#6は1サイクルあたりの停止時間が長いことが分かった。これにより、予測対象軌道の1サイクルあたりの停止回数・停止時間が予測距離誤差に影響を与えている可能性があることが分かった。
| 軌道# | 停止回数 | 合計停止時間[s] |
|---|---|---|
| 1 | 4 | 8 |
| 2 | 6 | 12 |
| 3 | 3 | 6 |
| 4 | 4 | 8 |
| 5 | 2 | 4 |
| 6 | 4 | 40 |
5.4 従来手法との比較
DBTを用いた本研究の予測手法の予測結果と比較するために、5.1の実験条件で取得した6つの軌道の体幹中心座標の時系列データを用いて、5.2の評価方法に従って、オーソドックスな時系列解析手法を用いた予測と評価を行った。
オーソドックスな手法として、ARIMAモデルとLSTMを採用した。
ARIMAモデルは、自己回帰和分移動平均モデルの略で、統計学で時系列解析に用いられる代表的な手法である8)。今回はPythonのDartsライブラリを使用した。単変量解析が可能のため、体幹中心座標XとYの学習器を別個に作成し、予測を行った。
LSTMはLong short-term memoryの略で、RNNの一種でより長期系列に対応できるようにしたのが特徴である9)。今回はPythonのDartsライブラリを使用した。多変量の予測が可能であるため、DBTと同様に体幹中心座標XとYを1つの学習器で同時に予測した。
3つの手法(ARIMAモデル、LSTM、DBT)により、6つの軌道に対する予測距離誤差と処理時間の評価結果を表5に示す。
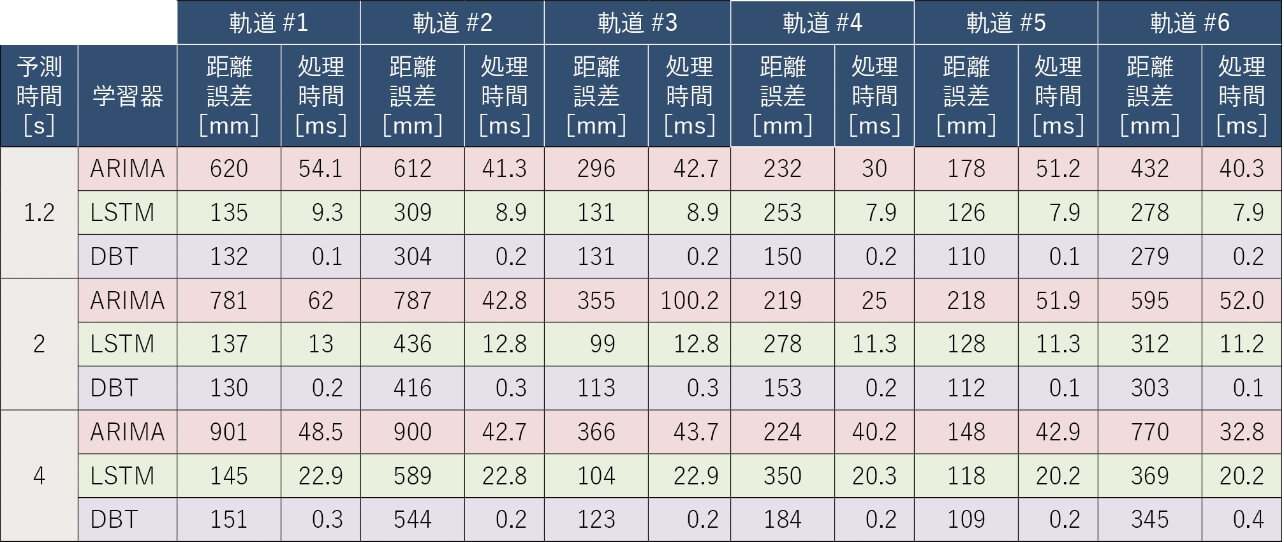
距離誤差に関しては、ほぼDBT < LSTM < ARIMAであることが確認できた。軌道#4においてはDBTの距離誤差がLSTMより著しく低く、他の軌道においてはLSTMと同等或いはやや低いことが分かった。
処理時間に関しては、DBT < LSTM < ARIMAであることが全軌道で確認でき、DBTの予測処理はLSTMより10倍以上速いことが分かった。
6. むすび
本研究では、スムーズな人ロボット衝突回避を実現するために、人体幹位置予測技術の性能指標と目標値を定義し、体幹中心座標を特徴量とすることをベースに、AIによる歩行軌道の予測技術を製造現場の人体幹位置予測に応用する手法を提案した。
U字型製造ラインの模擬環境によりその手法の効果を評価した。結果として、0.4msの処理時間で4s先の人体幹位置が予測可能であり、最大の予測距離誤差が544mmであることが分かった。また、比較評価実験により、本手法はオーソドックスな時系列解析手法より予測精度が優れており、処理速度が10倍以上速いことが分かった。
本手法の予測距離誤差に関して、目標を達成することができない、改善が必要であることが判明した。これについては、予測対象軌道の停止回数・停止時間が長いことに起因しており、次の行動予測が難しくなっている。対策として、例えば作業員の視線の追跡や停止時の手作業状態の監視など、次のアクションが推測できる情報を予測処理に加えることによってAIの判断精度を向上し、予測距離誤差が改善できないかと考えている。
今後は、予測距離誤差を改善し、製造現場事例を増やして評価することにより、本手法の実用性と汎用性を向上する。さらに複数人対応や手の動きの予測などの技術獲得を目指して研究を進め、最終的に、人の動き予測技術によりスムーズな人ロボット衝突回避を実現し、安全性と生産性が高度に両立する人ロボット協働生産環境の実用化に貢献していく所存である。
参考文献
- 1)
- 経済産業省.ものづくり白書2019版.経済産業調査会,2019, p.195-216.
- 2)
- 中央労働災害防止協会.機能安全活用実践マニュアル産業用ロボットシステム編.中央労働災害防止協会,2017, p.8-42.
- 3)
- Murray, S.; Floyd-Jones, W.; Qi, Y. “The Microarchitecture of a Real-Time Robot Motion Planning Accelerator”. 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture(MICRO). 2016, p.1-12.
- 4)
- Henrik Schumann-Olsen; Marianne Bakken; Øystein Hov Holhjem. Parallel Dynamic Roadmaps for Real-Time Motion Planning in Complex Dynamic Scenes. 3rd Workshop on Robots in Clutter, IEEE. 2014
- 5)
- Pellegrini, S.; Ess, A.; Schindler, K.; Van Gool, L. “You’ll never walk alone: Modeling social behavior for multi-target tracking”. 2009 IEEE 12th International Conference on Computer Vision. 2009, p.261–268.
- 6)
- Alahi, A.; Goel, K.; Ramanathan, V. “Social LSTM: Human Trajectory Prediction in Crowded Spaces”. 2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). 2016, p.961-971.
- 7)
- 金天海.“鍛造モデルによる機械特性学習”.第23回ロボティクスシンポジア予稿集,2018, 4C4.
- 8)
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control. San Francisco, Holden-Day, 1970, p.88-97.
- 9)
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation. 1997, vol.9, no.8, p.1735-1780.
DBTは、株式会社エイシングの日本における登録商標または商標です。
本文に掲載の商品の名称は、各社が商標としている場合があります。














