高角度分離分解能を有する到来方向推定を導入した交通監視用ミリ波レーダ
- ミリ波レーダ
- 自動運転
- 安全運転支援
- アンテナ制御
- 到来方向推定
安心・安全な交通環境を実現するために、安全運転支援や自動運転技術に対する期待が高まっている。とくに、交差点や合流部など、複雑な交通シーンが想定される地点においては、車両に搭載されたセンサだけではなく、インフラ側に設置されたセンサの情報も活用するインフラ協調型システムが重要な役割を果たすと考えられ、実用化に向けた研究開発が進められている。
当社では、周囲環境によらないロバストな検出性能が期待できるインフラセンサとして、ミリ波レーダの開発を進めている。ミリ波レーダは、アンテナ数の制約から角度分離分解能が光学系のセンサと比較して不利となりやすいため、とくに車両並走シーンの分離検出が難しい。今回、ミリ波レーダに高角度分離分解能を有する到来方向推定を導入し、実際の車両並走シーンを対象にして、検出性能評価をおこなった。その結果、並走車両の分離が可能になることを確認し、到来方向推定の有効性を示した。
1.まえがき
政府は、交通事故による年間死者数を2020年までに2500人以下に減らす目標を掲げている1)。死者数は年々減少しているものの、近年その減少数には下げ止まりの傾向がみられる2)。その他にも、主に都市圏における深刻な交通渋滞発生に伴う経済損失や、物流・移動サービスにおけるドライバー不足など、交通にかかわる社会的課題が数多く顕在化している。
これらの課題を解決し、安心・安全かつ快適な交通社会を実現するために、安全運転支援システムや自動運転技術に関する様々な研究開発が進められている。例えば、内閣府は戦略的イノベーション創造プログラム(SIP)において、自動運転を実用化し普及拡大することを目的として、産学官共同によるインフラ協調型自動運転システムの研究開発を推進している3)。
インフラ協調型システムでは、自動走行車両に搭載されたセンサだけでは検出が困難な、見通し外に存在する物体を検出するため、インフラ側に設けられたセンサの検出情報も活用する。レーダは、カメラやLiDARなどの光学系センサと比較して、電波を用いることにより周囲の照度変化の影響を受けず、また雨・霧に対する透過性が高いため、検出性能が天候や時間帯に影響されにくいという特徴を持ち、インフラセンサとしての利用可能性が注目されている。
当社は、次世代のインフラセンサとしてミリ波レーダの開発を進めており、その到来方向推定に高角度分離分解能手法を導入することで、車両の分離検出能力を高められることを実証した4)。本稿では、その詳細について紹介する。
2. ミリ波レーダの動作原理
2.1 距離・速度の推定
ここではFrequency Modulation Continuous Wave(FMCW)方式を例として、図1を用いてレーダの動作原理を説明する。FMCWレーダは、周波数変調された連続信号(チャープ信号)を送信し、物標によって反射された受信信号と送信信号の一部をミキシングして得られた差周波成分(ビート信号)をもとにして、距離測定をおこなうものである。受信信号は、チャープ信号に対して物標との距離に対応した往復電波伝搬時間ぶんだけ遅延して受信されるため、ビート信号の周波数は遅延時間、すなわち物標との距離によって定まる。時間信号であるビート信号をフーリエ変換により周波数領域に変換することで、レーダと物標間の距離を算出することができる。また、物標が移動している場合、ドップラ効果によってレーダと物標の相対速度に対応した周波数成分が受信信号に重畳するため、距離算出と同様にして、レーダに対する物標の相対速度を算出することができる。
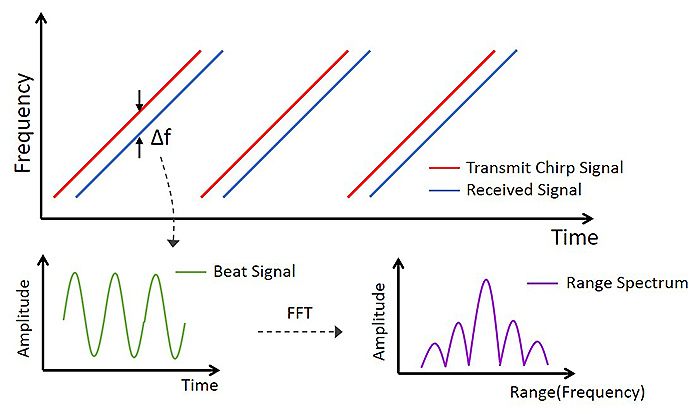
異なる距離に存在する2つの物標を分離検出可能な最小距離である距離分離分解能は、送信信号の変調帯域幅によって定まり、帯域幅が広いほど向上する。また、レーダは物標の速度を距離と同時に算出することができるため、速度に関する分離分解能も距離と同様に定義することができる。速度分離分解能は、フーリエ変換の性質からチャープ信号の繰り返し数の増加、すなわち観測時間が長くなるほど向上する。
ミリ波周波数帯は数百MHzから数GHzにわたる広帯域信号を利用可能であるため、高い距離分離分解能を実現することができる。また、周波数が高いほど電波の波長が短くなるため、対応するアンテナを小型化することができる。このため、ミリ波レーダは小型かつ高い距離分離分解能を実現することができる。
2.2 方位角の推定
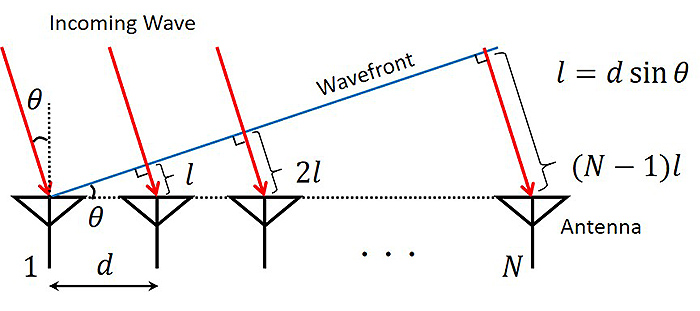
レーダのアンテナが複数のアンテナからなるアレーアンテナで構成され、かつ物標とレーダ間の距離がアレーアンテナの寸法よりも十分に大きい場合、入射波は波面が平面である平面波とみなすことができる。このとき、図2に示すようにレーダに対する物標からの反射信号は、受信アンテナごとに物標の方位角にもとづく経路長差をもって入射する。そのため、各受信アンテナにおける受信信号の間には、経路長差による遅延量の違い、すなわち位相差が生じている。この位相差をもとに、物標の方位角を算出することができる。ここで、角度分離分解能は、同距離に存在する2つの物標を分離検出可能な最小角度として定義される。
3.レーダに要求される分解能
表1は、車両走行の代表的なシーンと、レーダを用いてそれらのシーンで車両を分離検出する際に要求される分解能の種類を示している。
3.1 追従
複数台の車両が、同一車線で一定間隔を保ちつつ走行する場合においては、レーダから見て各車両が同一速度、同一角度となる。このとき、各車両を分離検出するためには、距離情報をもとに分離する必要がある。距離分離分解能は周波数帯域幅によって定まるため、周波数帯域幅を広くとることで分解能を向上させることができる。
3.2 追越し・追抜き
速度の速い車両が、遅い車両の前方に出る場合において、最も分離分解能が要求されるのは、各車線に車両が隣接して存在している場合である。この場合、レーダから見て各車両は同一距離となる。各車両を分離検出するためには、速度情報か角度情報のいずれかをもとに分離する必要がある。速度分離分解能は、観測時間が長くなるほど向上するため、観測時間を確保することで対応できる。
| シーン | 追従 | 追越し・追抜き | 並走 |
|---|---|---|---|
| イメージ |  |
 |
 |
| 要求される分解能 | 距離 | 速度/角度 | 角度 |
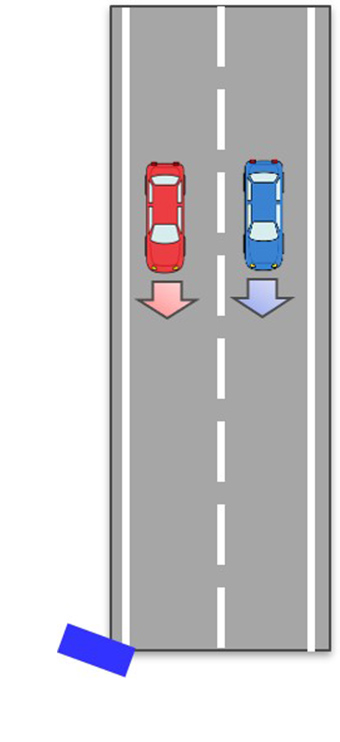
3.3 並走
複数台の車両が隣接車線を並びあって走行する場合においては、レーダから見て各車両が同一距離、同一速度となるため、角度情報をもとに分離する必要がある。光学系センサと比較して、レーダはアンテナ数の制約により角度分離分解能を高めることが難しいため、並走はレーダが苦手とする検出シーンのひとつである。
角度分離分解能は、本質的にはアンテナのビーム幅に依存しているため、アンテナ単体のビーム幅を狭くしたり、アンテナの数を多くしたりする必要がある。これらをアンテナの特性によって実現しようとする場合、前者においては検出エリアが狭くなるという問題があり、後者においてはレーダが大型化したり、コストアップに繋がるといった問題がある。したがって、限られたアンテナ数で車両を分離検出できる角度分離分解能を実現することが求められ
る。
この場合、物標の方位角を推定する到来方向推定手法の特性が重要になる。従来利用されてきたBeamformerはフーリエ変換にもとづく手法であり、その限界を超える手法が求められる。表2は、Beamformerと、それよりも高い分離分解能が期待できる到来方向推定手法の特徴を比較したものである。
LPとMUSICは、ともに高い角度分離分解能が期待できる手法だが、MUSICは受信信号の相関行列の固有値展開をおこなう点に特徴がある。ここで得られた各固有値(固有ベクトル)に対し、到来方向推定結果である角度スペクトルが得られるが、現実には雑音の影響などにより、誤った到来方向推定結果であるスプリアスが生じる場合がある。MUSICでは並列化による合成処理をそれらに適用したMUSICスペクトルを利用することで、スプリアスを低
減することができるという特徴をもつ。したがって、我々は従来のBeamformerに対して角度分離分解能の改善がもっとも期待でき、かつスプリアスの低減が可能な手法であるMUSICを到来方向推定手法として採用することで、インフラセンサとしてのミリ波レーダで従来不可能だった並走時の車両分離検出が可能になると考えた。
| 手法 | 概要 | 分解能 |
|---|---|---|
| Beamformer | メインローブを全方向に渡って走査し、アンテナからの出力が大きくなる方位角を算出 | アンテナで形成されるビーム幅に依存 |
| Capon5) | メインローブ以外の方位角度からの出力への寄与を最小化 | アンテナで形成されるビーム幅に依存 |
| LP6) | 出力電力を最小化するようにヌルを走査 | Beamformer/Caponより高い |
| MUSIC7) | 部分空間による信号と雑音の直交性を利用し、MUSICスペクトルを用いて走査 | LPと同等+スプリアス低減 |
4.実験
MUSICによる分離検出の改善効果を確認するため、実際の車両並走シーンを対象とした実験をおこなった。
4.1 検証用ミリ波レーダ
表3は、実験に用いたミリ波レーダの仕様を示している。アンテナ数が送信2、受信4のMultiple Input Multiple Output(MIMO)レーダであり、仮想アレーによる受信アンテナ数は8となる。周波数帯域幅と観測時間から定まる距離分離分解能と速度分離分解能は、それぞれ0.4m、1.0km/hであり、追従や追越し・追抜きの分離検出に必要な性能を備えている。
| 方式 | FMCW |
|---|---|
| アンテナ数 | 送信2、受信4 |
| 中心周波数 | 76.5GHz |
| 周波数帯域幅 | 340MHz |
| 観測時間 | 6.5msec |
4.2 実験環境
図3は、設置されたレーダから見た実験環境を示している。レーダの設置高はインフラセンサとしての設置環境を想定し、地上高6.75mとした。道路幅は5.8mであり、2車線を想定している。路肩から車両を監視するシーンを模擬し、レーダから奥行50mかつ図中に示す位置が0度となるようにレーダを設置した。2台の車両は、レーダに近づく方向に約30km/hで並走する。

4.3 実験結果
レーダからの距離30m地点を2台の車両が通過した際の角度推定結果から、並走車両の分離検出が可能かどうか検証をおこなった。
図4は、車両が30m地点を通過した際の受信信号にもとづいて計算した、距離と速度の推定結果を示している。車両がレーダに近づいてくるとき、負の速度として検出される。図中において、距離30m、速度-9m/s(-32km/h)にピークが出現していることがわかる。このピークは並走する車両を検出したものであるが、レーダに対して2台の車両が同距離・同速度で走行しているためにピークが同じ位置で重なっており、距離情報と速度情報にもとづく並走車両の分離検出ができないことを示している。
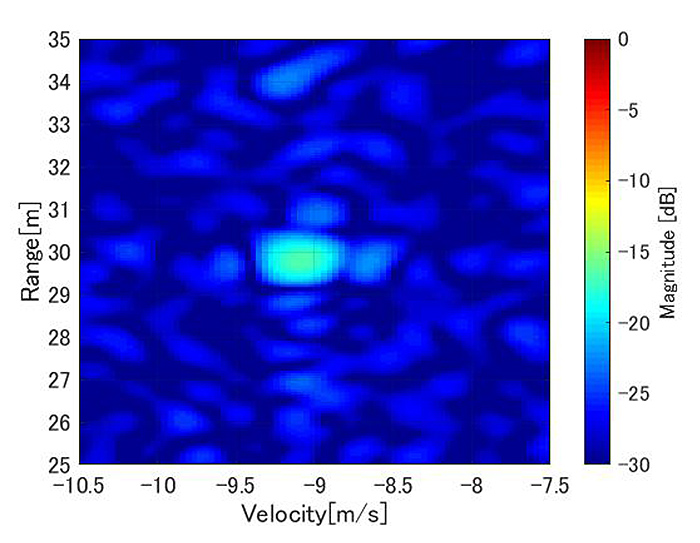
図5は、30m地点におけるBeamformerとMUSICを用いた場合の方位角推定結果を示している。表4は、並走車両のレーダに対する真の方位角(真値)と、図5から読み取った推定結果のピーク値を示している。ここでは並走車両に対応した2つのピークの出現が期待されるが、結果から両手法ともに分離検出できていないことがわかる。MUSICは、本来Beamformerよりも高い角度分離分解能が期待されるが、受信信号の相関行列の固有値展開を用いる手法であるがゆえに、複数物標からの反射信号の間で相関が高ければ、その性能が低下するという欠点がある。今回、並走車両という近接した物体の反射信号に対して、それが強く現れたものと考えられる。
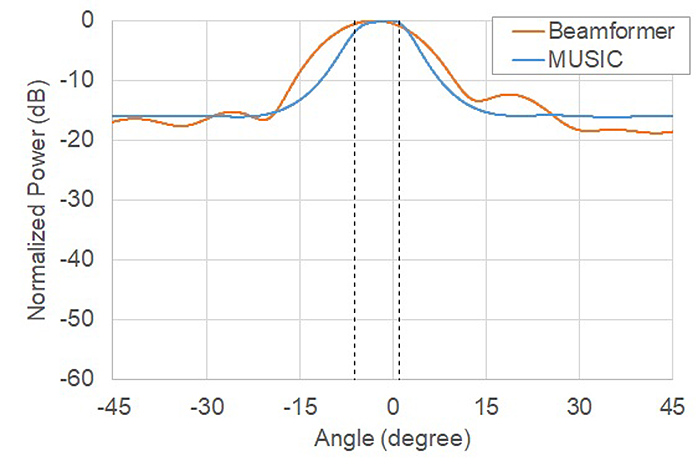
| 真値 | Beamformer | MUSIC | |
|---|---|---|---|
| 推定角度 | -6.2,+1.0deg | -2.9deg | -0.3deg |
これに対処するため、相関を抑圧する処理である空間平均法8)を適用した。空間平均法は、方位角推定において相関行列を計算するとき、全体のアレーアンテナ配列をサブアレーと呼ばれる複数の部分的なアレー配列に分割し、それらサブアレーの相関行列の平均をとるというものである。相関のある信号であっても、その位相は受信位置をずらせば変化するので、サブアレー化により受信位置をずらした状態を実現し、それを平均することで相関を抑圧する
ことができる。
図6は、MUSICの計算時に空間平均法を適用した場合の方位角推定結果を示している。MUSICの推定結果において、明確に2つのピークが出現していることがわかる。表5に示すように、2つのピークが示す推定角度はそれぞれ真値とよく一致している。
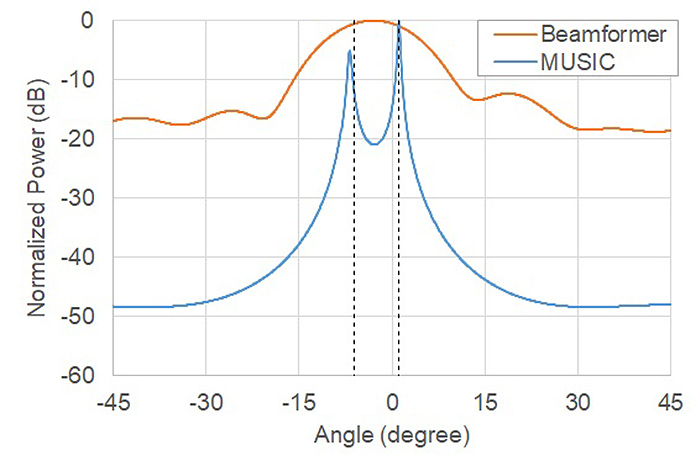
| 真値 | Beamformer | MUSIC | |
|---|---|---|---|
| 推定角度 | -6.2,+1.0deg | -2.9deg | -6.9,+1.1deg |
4.4 考察
MUSICの検出結果に対して、計算過程における相関行列から得られた到来波の受信電力と雑音電力の差(SNR)を計算した。物標を検出するためには、最低でも6dB程度のSNRを確保することが望ましい。表5に示す2つのピーク角度に対してSNRを計算したところ、それぞれ9.1dB(-6.2deg.)、9.9dB(+1.0deg.)となった。スプリアスであれば、SNRはほぼ0dB近くとなるため、今回得られた2つのピークはスプリアスではなく、車両由来のものと判断することができる。
以上のことから、空間平均法を適用したMUSICを用いることにより、従来手法であるBeamformerでは不可能だった並走車両の分離検出が可能になることがわかった。
5.むすび
インフラセンサとしてミリ波レーダの利用を想定し、とくに検出難易度が高い車両の並走シーンに対して、高角度分離分解能手法であるMUSICの適用により、車両分離検出が可能かどうか検証をおこなった。
路肩からの観測を模擬した実車両を用いた検証により、従来手法であるBeamformerでは不可能だった並走車両の分離が、MUSICでは可能になることを示した。また、並走車両からの反射信号に対しては、信号間の相関を抑圧するために空間平均法の適用が効果的であることがわかった。
以上のことから、インフラセンサとしてのミリ波レーダにおいて、従来手法では不可能だった並走車両の分離が可能になることを示した。
今後は、さらに様々な環境において評価実験をおこなうほか、同じアンテナ構成のまま角度分離分解能の向上が期待できるKhatri-Rao積による仮想アレー拡張手法9)など、さらなる高角度分離分解能手法の適用や、検出エリアに適したアンテナ性能の最適化を進めていく。
謝辞
本稿は、国立大学法人新潟大学との共同研究成果の一部である。新潟大学 山田寛喜教授、堀内貴裕氏に深く感謝申し上げる。
参考文献
- 1)
- 中央交通安全対策会議.“第10次交通安全基本計画”.内閣府.2016-03-11. https://www8.cao.go.jp/koutu/kihon/keikaku10/index.html,(参照 2019-08-05).
- 2)
- 交通局交通企画課.“平成30年中の交通事故死者数について”.警察庁.2019-01-04.http://www.npa.go.jp/news/release/2019/20190104jiko.html,(参照 2019-08-05)
- 3)
- 内閣府.“東京臨海部実証実験の実施について~ SIP「自動運転(システムとサービスの拡張)」~”.内閣府.2018-11-13.https://www8.cao.go.jp/cstp/stmain/20181113_adusrinkai.html,(参照 2019-08-05).
- 4)
- 上野大,堀内貴裕,杉井裕太,齋藤啓介,山田寛喜.“ミリ波レーダにおける到来方向推定を用いた車両分離に関する検討”.2019 年電子情報通信学会総合大会.2019,p. 165, B-1-165.
- 5)
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE. 1969, Vol. 57, No. 8, p. 1408-1418.
- 6)
- Tufts, D.W.; Kumaresan, R. Estimation of frequencies of multiple sinusoids: Making linear prediction perform like maximum likelihood. Proc. IEEE. 1982, Vol. 70, No. 9, p. 975-989.
- 7)
- Schmidt, R. O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. 1986, Vol. AP-34, No. 3, p. 276-280.
- 8)
- Shan, T. J.; Wax, M.; Kailath, T. On Spatial Smoothing for Estimation of Coherent Signals. IEEE Trans. 1985, Vol. ASSP-33, No. 4, p. 806-811.
- 9)
- Ma, W.-K.; Hsieh, T.-H.; Chi, C.-Y. DOA Estimation of Quasi- Stationary Signals With Less Sensors Than Sources and Unknown Spatial Noise Covariance: A Khatri – Rao Subspace Approach. IEEE Trans. 2010, Vol. SP-58, No. 4, p. 2168-2180.
本文に掲載の商品の名称は、各社が商標としている場合があります。














