アーク遮断現象を定量化するシミュレーション技術
- リレー高容量化
- アークシミュレーション技術
- 電磁熱流体解析
- 環境エネルギーマネジメント機器
- 遮断性能向上
近年、環境問題への関心の高まりから再生可能エネルギーの高効率化が急務とされている。効率を高めるためにシステムは高電圧あるいは高電流化が進んでいる。したがってシステムに利用されるリレーにおいても高容量遮断性能が求められるようになった。これを実現するためには、遮断時に接点間に発生するアーク放電のメカニズムを理解し、制御方法を確立しなければならない。
そこで本検討では、アーク挙動を定量的に評価し、アーク遮断メカニズムを詳細に把握するため電磁熱流体モデルを用いたアークシミュレーション技術の構築を試みた。
アーク挙動のシミュレーション結果と実測との比較により、高い再現性があることを確認した。さらに構築したシミュレーション技術を用いて、磁気消弧におけるアーク遮断メカニズムを明らかにした。この技術はアーク放電のメカニズム解明に役立ち、今後のアーク挙動の制御方法確立に貢献できる。
1.まえがき
地球温暖化などの環境問題に対する意識の高まりや原油の高騰などを背景に、再生可能エネルギーや電気自動車の市場が拡大している。それらに用いられるエネルギーマネジメント機器やバッテリー制御回路においては、高絶縁性と低抵抗の観点から直流リレー(以下、リレーと呼ぶ)が使用されている。
リレーでは開極時に接点間で絶縁破壊が起こり、アーク放電(以下、アークと呼ぶ)が発生する。アークとは空気などの気体が数千度以上の高温1)となり気体分子が電離および解離することで気体の電気伝導率が増加し2)、気体中に電流が流れる現象である。このとき電流によるジュール発熱でアーク導電経路の温度が維持されることにより、アークが継続する。アークが継続するとアークにより高温状態となり、筐体内部の損傷や接点の消耗が起こる。これら機器の破損は火災などの重大事故につながる可能性がある。近年では数百ボルトの高電圧あるいは数百アンペアの大電流での遮断が求められることが多く、従来にも増して安全かつ確実にアークを遮断できることが重要となっている。
限られたスペースで直流の高電圧あるいは大電流を遮断するためには、電極の開閉時に生じるアーク挙動を予測し制御することが重要な技術課題となる。アーク挙動を左右する要因には、アーク発生時の温度場や圧力場、アークに発生するローレンツ力3)などにより生成される流れ場などがある。
これまでアーク挙動を把握するため電気波形計測や高速度カメラによる観察が行われてきた。しかしながらそれらの観察ではアーク挙動を左右する要因である温度場や圧力場、流れ場を把握することは難しい。そこでこの課題を解決するためCAE(Computer Aided Engineering)によるシミュレーション技術に着目した。CAEを用いることにより温度場や圧力場、流れ場を解析でき、これらがアーク挙動にどのような影響を与えているか定量的に評価できる。これはアーク遮断に至るまでのメカニズムを把握することにつながり、リレーの性能を高めていく上で非常に効果的である。
そこで今回、CAEを用いて熱流体解析と電磁界解析を連成させたアークシミュレーション技術の構築に取り組んだ。シミュレーションする内容は接点開閉時に発生するアーク挙動であり、汎用の熱流体解析ソフトウェアの標準機能をベースに構築した。
本稿では、その取り組みについて、以下の構成で述べる。
第2章では、アーク挙動を記述するための仮定および支配方程式について述べる。
第3章では、解析モデルの詳細設定および、実測結果との比較をもってアークシミュレーション技術の妥当性を検証した。
第4章では、磁束密度を高くするほどアーク遮断時間が短くなる実験事実に着目し、複数の磁束密度の条件における解析結果を元に磁束密度とアーク継続時間との関係性について考察した。
第5章では、本解析モデルにおける課題と今後の展望について述べる。
2. アークシミュレーション手法
2.1 アークの取り扱い
アークシミュレーション技術を構築するにあたっての主な仮定を以下に示す。
- (1)
- 計算空間のすべての箇所で局所熱平衡(LTE=LocalThermodynamic Equilibrium)が成立する。すなわち、電子温度、ガス温度、励起温度などの温度は全て等しく一温度で記述できる。電離および解離などの反応はすべて平衡状態となっている4)。
- (2)
- 流れ場は乱流(Transition SST モデル)を考慮する。
- (3)
- 電極は溶融・変形しないものとする。
ここで局所熱平衡モデルについて説明する。アーク内部では種々の解離、励起、電離、再結合が同時に起こっているが、1気圧以上の高気圧アークの場合はほぼ熱平衡状態にあり、アーク内の電子、中性粒子、イオンの温度は等しいと考えてよい。ただし、アーク内の各位置で平衡状態は異なるため、このような状態を局所熱平衡と呼ぶ5)。
2.2 支配方程式
局所熱平衡を仮定することにより、アークは電磁熱流体としてり扱うことができる。アークの電磁熱流体としての挙動は以下の質量・運動量・エネルギーの保存則により記述できる6)。気体の熱力学・輸送特性は温度に依存した物性値として方程式内で取り扱うことができる。
| 質量保存則 | |
 |
(1) |
| 運動量保存則 | |
 |
(2) |
| エネルギー保存則 | |
 |
(3) |
| 電流保存則 | |
 |
(4) |
| オームの法則 | |
 |
(5) |
| ベクトルポテンシャル | |
 |
(6) |
| 磁場 | |
 |
(7) |
| 電気回路の式(キルヒホッフの法則) | |
 |
(8) |
ここで、




















本解析モデルでは電極を取り囲む空間(以下、消弧空間)に充填する気体は空気を想定している。空気の質量密度、粘度、熱伝導率、比熱、電気伝導率、放射損失は、THERMAL PLASMA で報告されたものを用いた7)。
3. 解析モデルの妥当性検証
3.1 解析モデルについて
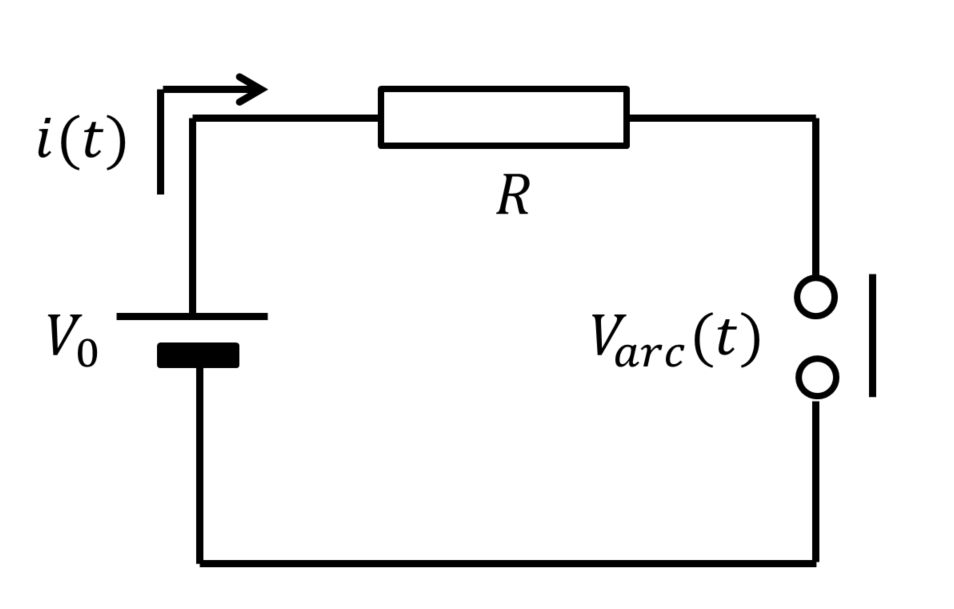
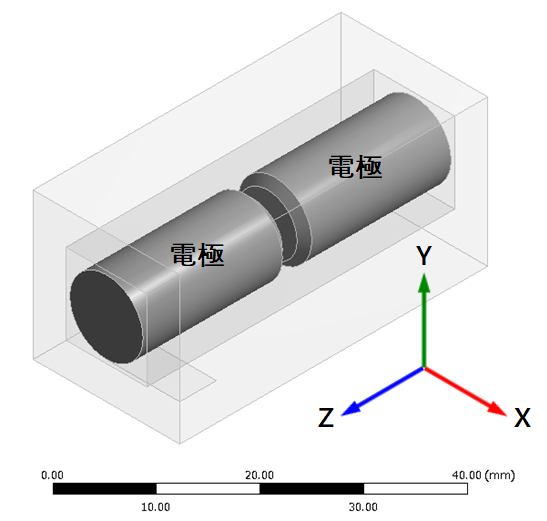
本アークシミュレーション技術では、直流アークを想定している。図1 に示す直流電気回路の接点部分を取り出し、図2 に示す解析モデルを作成した。解析モデルに用いた設定値を表1 に示す。
| 項目 | 設定値 |
|---|---|
| 空間サイズ | 42mm×20mm×20mm |
| 電極長さ | 20mm |
| 電極径 | Φ5mm |
| 接点間距離 | 2mm |
| 負荷条件 | 200V 60A |
| 磁束密度 | +Y方向に一様磁束 |
直流アークの遮断では消弧空間に磁石を配置し、ローレンツ力でアークを伸長させて遮断する磁気消弧が一般的である。それに倣い、本解析モデルでも消弧空間内に一様磁束を与えた。
3.2 アーク挙動の再現
図3 に磁気消弧時のアーク形状を示す。図3 の上段がCAE でのアーク温度コンター図(温度5000K 以上)、下段が高速度カメラで実測したアーク形状である。接点間でのアーク発生からアーク遮断完了までのアーク形状変化の解析結果は実験結果をよく再現している。
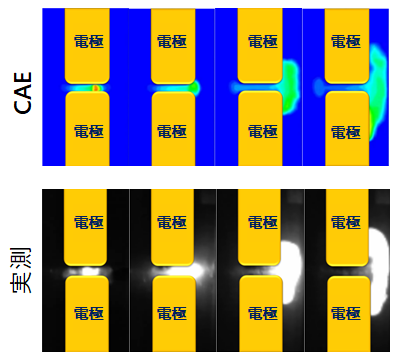
図4 にアーク遮断時のアーク電流およびアーク電圧波形を示す。アーク電圧の上昇やアーク電流の減少についても解析結果は実験結果をよく再現している。これらの比較結果より、アーク挙動を再現できたと判断した。
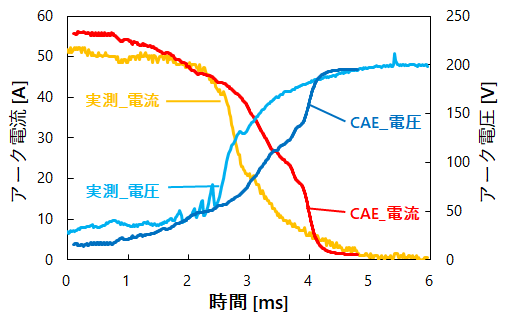
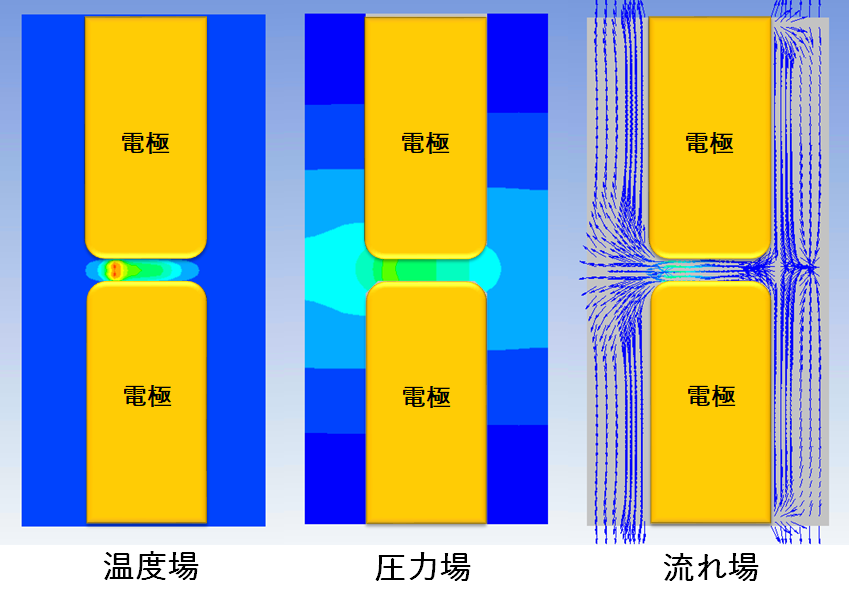
図5 に温度場と圧力場と流れ場のコンター図を示す。アークシミュレーション技術の構築により、これまで実測で見ることが難しいとされていたアークの3 次元挙動や温度場、圧力場、流れ場などを可視化できるようになった。
4. アーク磁気消弧メカニズムの解明
4.1 遮断性能向上の検討
先に述べたように高容量あるいは大電流での直流アーク遮断方法としては磁気消弧が一般的である。磁束密度を高くすることで早期にアーク遮断できることが実験事実として知られている。
そこで本検討では磁束密度とアークの挙動との関係性を把握するために4水準(20mT、40mT、70mT、85mT)の磁束密度にてアーク放電解析を行った。
4.2 アーク継続時間とアーク形状の関係性
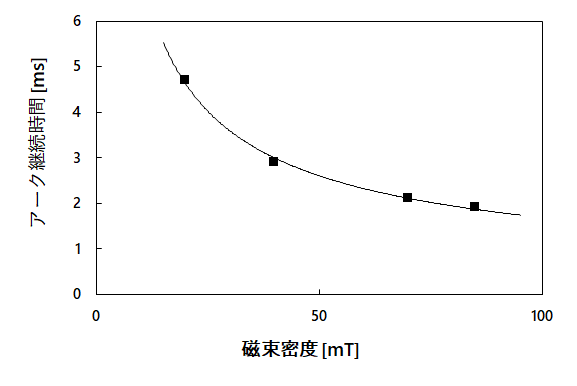
図6に磁束密度とアーク継続時間の関係を示す。図より磁束密度が大きくなるにつれ、アーク継続時間が短くなることが分かった。磁束密度とアーク継続時間の関係は線形的減少ではないことから、ある一定の値に収束していくことが予測される。これより、永久磁石を選定する際は一定以上の磁束密度を確保する必要があるが、ある閾値を超えると遮断時間が一定値に収束していくと考えられる。
今回アークシミュレーション技術の構築により実測では困難とされる3次元データ取得が容易となった。そこでアーク遮断において密接に関係するアーク形状に着目した。特にアーク長及びアークの太さ(以下、アーク径)は、アークの抵抗率に大きく関わるため関係性を明らかにする必要がある。
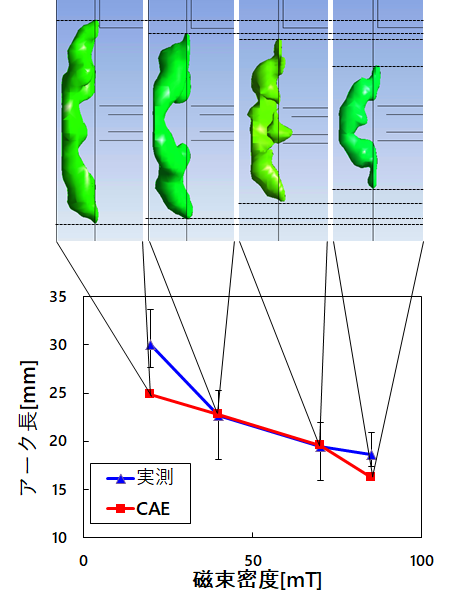
図7に磁束密度とアーク長の関係を示す。CAEによる結果では各磁束密度における遮断直前の温度場の等位面(5000K)からアーク長を算出した。また実測では画像より発光強度の高い部分から中心を導出し、その中心線の長さからアーク長を算出した。図7より解析および実測ともに磁束密度の増大に伴い、アーク長が短くなる傾向を確認した。
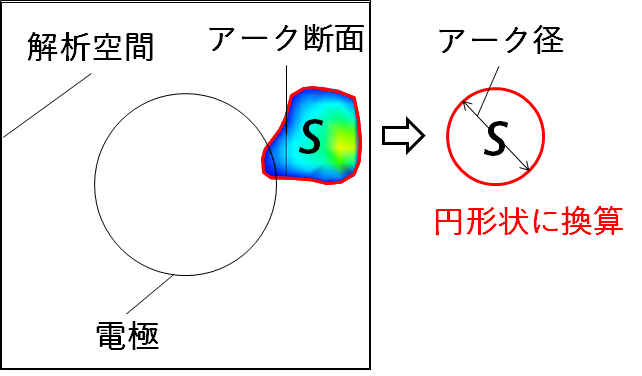
アーク径の定義を図8に示す。アーク径の定義はアーク(温度5000K以上)を端子中心軸に対して垂直方向で切断した断面積を円形状に換算した際の直径とする。
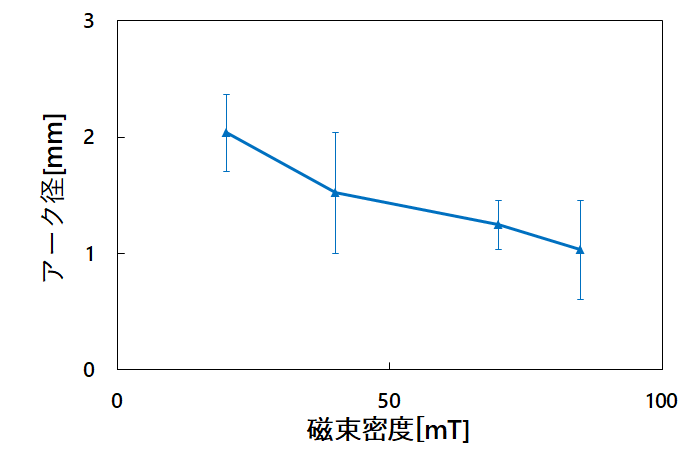
図9に磁束密度とアーク径の関係を示す。ここでは各磁束密度における遮断直前のアーク径とした。図9より磁束密度が大きくなるに伴い、アーク径は小さくなる傾向を確認した。
4.3 考察及びメカニズム解明
前節より磁束密度を大きくすると、アーク長は短く、アーク径は小さくなることを解析上明らかにした。一般的にアークを遮断するためには、アーク抵抗

しかし磁気消弧では磁束密度が大きくなると、アーク長が短くなることが実測および解析結果から分かっており、負荷電流・電圧・アーク長のみで磁気消弧の遮断メカニズムを説明できない。そこでアークシミュレーション技術の構築により取得可能となったアーク径及び温度場の結果を用いて磁気消弧の遮断メカニズムについて考察をおこなった。アーク抵抗
 |
(9) |
ここで、

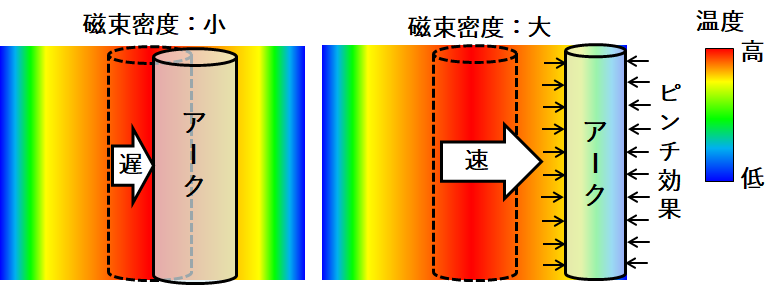
この式から、磁束密度によりローレンツ力を大きくすることで、アーク径の低減、すなわち、アーク断面積の低減に伴うアーク抵抗
熱的ピンチ効果によりアーク断面積が小さくなりアーク抵抗
本検討では今回構築したアークシミュレーション技術を用いることでアーク磁気消弧メカニズムを定量的に明らかにした。
5. むすび
従来の実測評価で把握できていなかった温度場や圧力場、流れ場などを定量的に評価することがリレーの性能を高める上で効果的と考え、アークシミュレーション技術に取り組んだ。2次元断面でのアークの挙動の実測結果およびアーク遮断時の電流・電圧波形との比較をもって妥当性を検証し、アークシミュレーション技術の構築を完了した。
本技術によりアークの3次元挙動や温度場、圧力場などの可視化が可能となった。本検討では磁束密度を大きくすることで、遮断時間が短くなるメカニズムを考察した。アークにかかるローレンツ力が大きくなることで、アークの移動速度が上がりアーク周囲が冷却される。それによりアーク断面積が小さくなることでアーク抵抗が増大しアーク遮断時間が短くなったと考察した。
本稿ではアーク形状の3次元データと温度場を中心にアーク遮断のメカニズムについて検証を行った。今後は圧力場・流れ場がアーク挙動に与える影響についても検証し、遮断性能向上につながる制御方法の確立に取り組む。これにより、高電圧あるいは大電流のアークを安全かつ確実に遮断できるリレーを開発し、再生可能エネルギー社会の実現に貢献していく所存である。
参考文献
- 1)
- Y. Aoyama et al., Spectroscopic analysis for the arc quenching effect of ablation gas on arc immobility phenomena. Thirty-Sixth IEEE Conference on Electrical Contacts, and the Fifteenth International Conference on Electrical Contacts. Aug. 1990
- 2)
- Y. Cressault et al., Influence of metallic vapours on the properties of air thermal plasmas. Plasma Sources Sci. Technol. 17. 2008, p.1-9. IOPscience,.
- 3)
- H. Miyagawa et al., Effect of Magnetic Blow-Out and Air Flow on Break Arcs Occurring between Silver Electrical Contacts with Copper Runners. IEICE TRANS. ELECTRON., Sep. 2017, VOL. E100-C, No9.
- 4)
- 渡辺隆行,田代真一.熱プラズマの解析に用いられる電磁熱流体モデル.J. Plasma Fusion Res. 2011, Vol.87, No.8, p.514-521.
- 5)
- 電気学会放電ハンドブック出版委員会.放電ハンドブック.電気学会.2003, p.1945.
- 6)
- 田代真一,田中学,中田一博,輿石房樹,鈴木啓一,山崎圭.Ar-He 混合ガスタングステンアークにおける熱輸送特性の数値シミュレーション.高温学会誌.2006, Vol.32, No.1,p.69-73.
- 7)
- Maher I. Boulos et al., THERMAL PLASMA Fundamentals and Applications. Vol.1, PLENUM PRESS, 1994, 452p.
- 8)
- 森口裕亮,榎本英樹,山本律,福田純久,尾崎良介,池田陽 司.EV・HEV 用大電流メインリレーの小型化技術.Panasonic Technical Journal. May 2015,Vol.61, No.1, p.72-76.
- 9)
- H. Ayrton. The Electric Arc. New York: D. Van Nostrand, 1902,528p.
- 10)
- 佐藤充典.電気接点-材料と特性.日刊工業新聞社,1984,191p., ISBN-10:4526017299.
- 11)
- M. Tanaka et al., 溶接アークの熱的ピンチ効果に関する一考察.溶接学会論文集.2007, Vol.25, No.2, p.336-342.
本文に掲載の商品の名称は、各社が商標としている場合があります。




















