動的線型モデルによるコールセンターの受信コール数予測
企業の問い合わせ窓口など、顧客から受信したコールへの対応を主業務とするコールセンターでは、サービス品質とコストのトレードオフを抱えており、これを最適化するようなオペレータ配置を行うことが求められる。この際、将来の受信コール数を精度よく予測する必要があるが、予測プロセスが担当者の「経験と勘」に頼っている現場も多く、手間がかかる、予測精度が担当者に依存する、といった課題を抱えており、適切な予測モデルによる自動化が求められている。コール数予測モデルは、受信コール数の時系列のゆるやかな変動と、特定の条件でのみ生じる特異な変動をうまく扱える必要があり、現場の知見を明示的に反映できることが望ましい。このような性質を備えたモデルとして、動的線型モデルが挙げられる。このモデルにはさらに、予測の不確実性を定量化し、オペレータ配置に反映できるという利点もある。
本稿では、実際のコールセンターの受信コール数データについて、動的線型モデルによって2カ月先までのコール数を予測した結果を検証し、コール数を妥当な精度で予測できており、オペレータの過剰配置を39%削減する結果につながっていることを示した。
1. まえがき
オムロン フィールドエンジニアリンググループ(OFE)は、全国140箇所の拠点と1,200名のカスタマエンジニアによるサービスネットワークを構築し、エンジニアリングサービス/フィールドサービス/バックアップサービスを全国の顧客に提供している。このサービスを提供するうえで、コールセンター業務が重要な機能のひとつとなっている。コールセンターで行われる業務には大きく2種類があり、ひとつは電話勧誘販売のように自ら消費者等にコールを行うアウトバウンド業務、もうひとつは問い合わせ窓口などの受信したコールに対応するインバウンド業務である。OFEのコールセンターではこのうちのインバウンド業務を主に扱っており、受信したコールのうち既定の時間内に応答できたコールの割合がサービス品質の重要な指標のひとつとなっている。そのため、受信コールに対して十分な数のオペレータを用意する必要があるが、オペレータの確保には人件費等のコストが発生するため、サービス品質とコストのトレードオフを適切にバランスさせるようにオペレータ数を最適化する必要がある。OFEでは、時間ごとの平均コール数と平均コール時間から、サービス品質の要求水準を満たすことのできるオペレータ数を算出し、それに応じて人員を割り当てている。ここで、将来時点のコール数とコール時間は未知であり、過去のデータからの予測値を用いてオペレータ数を算出することになるため、コール数やコール時間の予測精度が重要となる。
単純な予測手法としては、前月の平均や前年同月の平均、曜日ごとの平均などをそのまま用いる方法があるが、コール数の変動がより複雑な場合には、それだけではうまく予測できず、担当者がコールセンター固有の変動要因も加味して「経験と勘」で予測値を調整するというようなオペレーションが採用されることも多い。このようなオペレーションでは、予測作業に手間がかかる、予測精度が担当者に依存する、などといった課題がある。
こうした課題を受け、様々なコール数予測手法が提案されている。一例としては、ARIMA や指数平滑等の一般的な時系列解析モデルによる予測が挙げられる1) が、これらのモデルは時系列の周期的な変動はうまく扱うことができるが、特定の日付のみ特異な変動を示すようなパターンを扱うことは難しい。このような特異な変動を扱える予測手法としては、重回帰モデルによる予測などが考えられる2)。重回帰モデルでは、年、曜日、週番号などの暦の情報に加え、各コールセンターに固有の変動要因を明示的に加味することが容易であり、説明性の高いモデルを作ることができる。しかし、重回帰モデルでは、平均値や各変動要因の影響の大きさが徐々に変化していくような、非定常な系列の扱いが難しく、そのようなデータに対しては時間とともにモデルの予測精度が低下していく恐れがある。実際のコール数データでも、平均や変動の大きさが時間とともに変わっていくようなパターンが観測されており、そのような変化を適切に扱えるモデルが必要と考えられる。
状態空間モデルと呼ばれるモデルのひとつである動的線型モデルは、複数の変動要因を持ち、非定常性や構造変化、不規則パターンがある時系列データを柔軟に扱うことができるモデルであり3)、コールセンターに固有の変動要因を容易に加味できることに加え、長期的なゆるやかな変動に追従する形で予測を行うことができる。さらに、予測結果の不確実性を確率分布の形で算出できるという特徴があり、予測結果と実際の結果の誤差がどのような確率で発生し、どの程度の大きさになるのかを定量的に評価することができる3)。得られた誤差の確率分布を活用することで、予測結果からの誤差が大きくなる可能性が高いと予測された日には、予測された誤差の大きさに応じてオペレータ数を増やしてリスクを軽減する、というような対応が可能になると期待される。
本稿では、OFE のコールセンターで扱っているATM 関連の金融機関からのコール数データに対して、動的線型モデルによる予測を行った結果を検証し、2カ月先までのコール数を妥当な精度で予測できており、予測精度の向上がより適切なオペレータ配置の決定に貢献できていることを確認した。
本稿の構成を以下に示す。2章では、コール数の特性について述べる。3章では、動的線型モデルの紹介、および具体的なモデルについて述べる。4章では、実データについて予測を行った結果について述べる。
2.コール数の特性について
2.1 全体の傾向
図1に、OFEのコールセンターにおける、2015年4月1日から2018年3月31日までの1日ごとの金融機関からのコール数をプロットしたものを示す。まず平日と土曜および休日ではコール数が大きく異なっていることがわかる。また、平日のコール数の動きにはある程度の季節性が見られるものの、その変動幅は安定しておらず、全体として非定常な系列となっている。なお、図1中の実線は平日のコール数の移動平均を示しており、季節要因が加わったうえでのトレンドとしてみることができる。
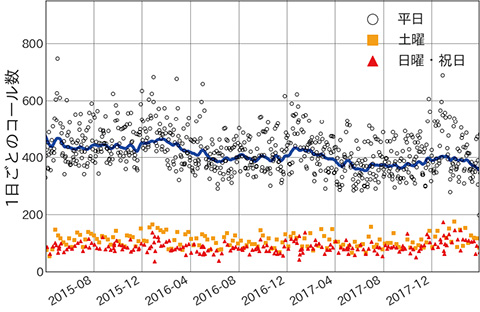
2.2 コールセンター特有の傾向
多くのコールセンターでは、コール数の増減に寄与するそれぞれ特有の傾向があると考えられる。現場の関係者へのインタビューやデータの観察を通してこのような傾向を見つけ出し、予測に取り入れることで、より精度の高い予測が可能になると考えられる。
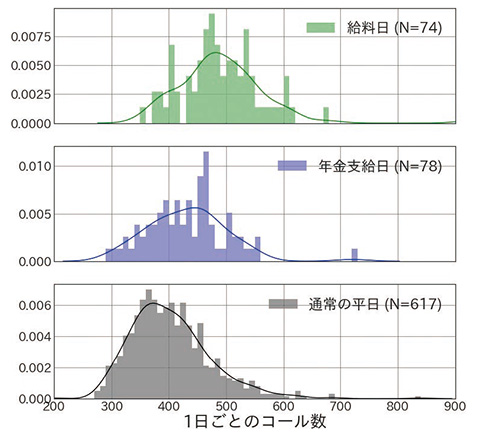
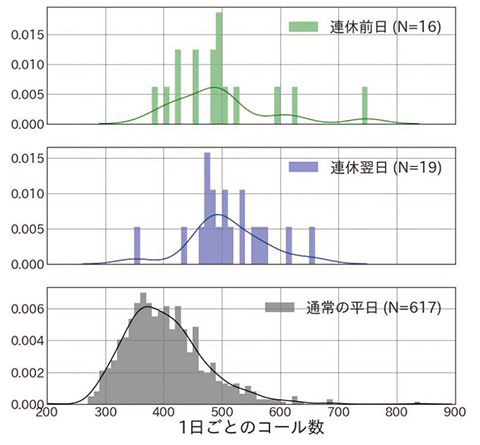
OFE のコールセンターではATM 機器についての金融機関からの問い合わせを取り扱っており、給料日となることの多い毎月25日や、年金支給日である毎月15日、また連休前後など、普段よりもATMの利用が多いと考えられる日にはコール数が多いという傾向が現場の「経験知」として以前から知られており、データの分析を通して実際にそのような傾向があることが確かめられた(図2、 3)。
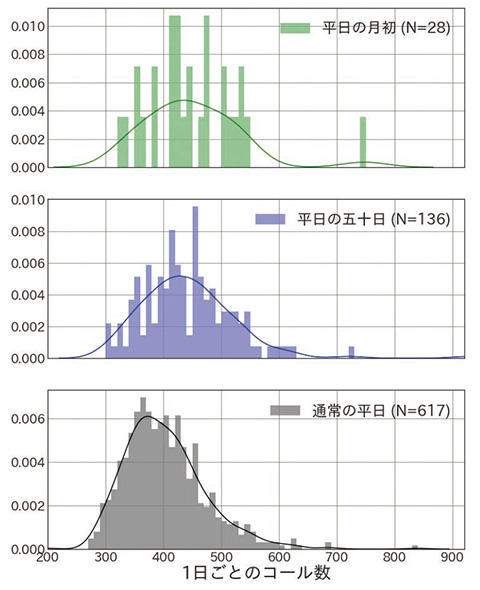
一方で、経験的に増減要因として扱われているものであっても、データを確認すると大きな変化がないという場合もあるので、実際に増減の要因となっているのは何なのか、注意深く検討する必要がある。例として、月初や五十日と呼ばれる5の倍数となる日にはコール数が増えるとされていたが、データからは大きな差は認められなかった(図4)。
OFE担当者へのヒアリングを通じて候補に挙がった変動要因について、コール数への影響の大きさを検討した結果、表1に示す9項目を特殊なコール数変動要因として予測モデルに取り入れることとした。
| 要因名 | 詳細 |
|---|---|
| 土曜日 | 土曜日 |
| 日曜・祝日 | 日曜日および国民の祝日 |
| 年始営業日 | 年始営業日 |
| 年末営業日 | 12/20以降の営業日と12月の金曜日 |
| 月末 | 月の最後の営業日 |
| 給料日 | 毎月25日(土日祝に重なる場合はその前で一番近い 平日)と翌営業日 |
| 年金支給日 | 毎月15日(土日祝に重なる場合はその前で一番近い 平日)と翌営業日 |
| 連休前日 | 3日以上の連休の前日 |
| 連休翌日 | 3日以上の連休の翌日 |
3.コール数の予測手法について
3.1 重回帰モデル
2章で述べたような特異な変動要因を含む時系列データの分析に従来用いられてきた手法である2)、重回帰モデルを紹介する。重回帰モデルは、式(1)の形で表され、対象を N 個の説明変数 Xi の線型結合とみなし、各 Xi の係数 ai および定数項 b を過去のデータに基づき算出することで特定化されるモデルである。
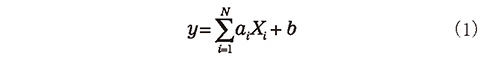
説明変数として、年月、曜日などの時系列要因を加えることで、時系列分析に応用することができる。また、時系列以外の変動要因も容易に付け足すことができ、コールセンターに特有のコール数変動要因を簡単に記述することができる。
ただし、重回帰モデルでは、時間が経つにつれ平均値が変わっていくような、非定常な系列を扱うことが難しい。図1に見られるように、OFEのコールセンターでは、コール数の平均が年を経るごとに変化していっており、このようなデータに対しては、より柔軟に非定常な時系列を扱えるモデルが望ましい。
3.2 状態空間モデルと動的線型モデル3)
上記のような特徴を持つモデルとして、状態空間モデルが挙げられる。状態空間モデルは、非定常性や構造変化、不規則パターンがある時系列にも適用できる高い柔軟性を持つモデルであり、そのうちモデルの線型性とノイズがガウス分布に従うことを仮定した場合を特に動的線型モデルと呼ぶ。
状態空間モデルでは、観測値 Yt の変動を直接モデル化するのではなく、状態過程と呼ばれる観測不可能なマルコフ連鎖 θt が存在し、時系列 Yt は θt に誤差が加わった不正確な観測値であると仮定する(図5)。このような仮定に基づき補助的な時系列 θt を取り入れることで、複雑な変動モデルを持つ時系列 Yt の確率分布の推定が容易になる。

動的線型モデルの場合の定式化を以下に示す。観測値 Yt は p 次元、状態 θt は q 次元とする。初期値 θ0 は、 θ0 ~ Nq(m0, C0) で与えられ、平均 m0 、共分散 C0 の q 次元ガウス分布に従う。また、 t ≥ 1 における Yt 、θt は
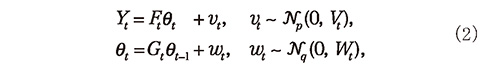
と表される。ここで、Ft と Gt は観測行列および遷移行列とよばれ、それぞれ時刻 t での観測 θt →Yt に伴う写像と前時刻からの状態の変動 θt−1→θt に伴う写像を表している(それぞれ p 行 q 列 、q 行 q 列)。また、vt は θt−1→θt の状態遷移で生じる誤差(システム誤差)を、wt はθt の観測 θt →Yt で生じる誤差(観測誤差)を表しており、それぞれ平均0、共分散 Vt 、Wt の多次元ガウス分布に従う確率変数とする。ガウス分布の和で表される確率変数はガウス分布に従うことから、 Yt と θt はそれぞれ p 次元、q 次元のガウス分布に従うことに注意する。
モデルの学習は、これら Yt 、θt が従うガウス分布の平均と分散に、各パラメータを観測されたデータをよく表すような値を選択するというプロセスで行われる。パラメータの選択にはいくつかの方法が考えられるが、データ全体を用いて最尤推定を行うことが多いため、ここでは最尤推定によりモデルのパラメータを特定するプロセスを紹介する。
n 個の観測値が従う確率変数 Y1, ..., Yn があり、その分布が未知のパラメータ ψ に依存しているとする。観測値として y1, ..., yn が得られたとき、尤度関数 L は観測値の同時確率密度を用いて L(ψ)= p(y1, ..., yn ;ψ) と表せる。ここで、観測値の同時確率密度は
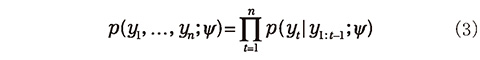
と書くことができるが、この右辺に現れる項がガウス分布の確率密度になる場合、その平均と分散 ft 、Qt を用いて、対数尤度 ℓ は以下のように書くことができる。
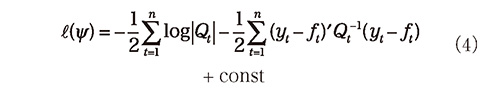
ここで、 ft と Qt は ψ に依存している。未知パラメータ ψ の最尤値φは、ℓ(ψ)を最大化する ψ を数値的に計算することで求めることができる。すなわち、
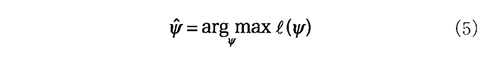
となる。
3.3 動的線型モデルの定式化
2章で述べたコール数の特性を踏まえ、以下のようなアイデアに基づきコール数予測モデルを作成した。
まず、各日でのコール数の期待値は、ベースとなる平日のコール数期待値に、図1に示した変動要因による差分を足し引きしたものと考える。また、平日のコール数期待値、各変動要因により生じる差分の大きさは、日ごとにランダムに変動しており、さらに、実際に観測されるコール数は、この期待値にランダムなズレが加わったものになるとする。
このとき、各日のコール数、変動要因による増減の大きさ、およびこれらが日ごとに変動する大きさがそれぞれガウス分布に従うと仮定することで、以上のモデルは動的線型モデルの枠組みで以下のように定式化される。
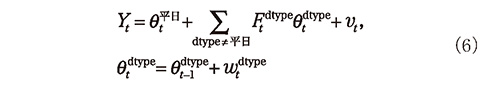
ここで予測すべきコール数を Yt とし、ベースとなる平日におけるコール数、および変動要因による差分を θtdtype により表している。ただし、dtype は日付の属性を示すフラグであり、平日、または表1に示した9個の変動要因のうちいずれかに該当する値を取る。また、 Ftdtype は日付 t が dtype であるときに1、それ以外の時は0を取る変数であり、 vt 、wtdtype は、平均0のガウス分布に従う観測誤差とシステム誤差である。このモデルの観測誤差とシステム誤差の従うガウス分布の分散値を、2015年4月1日から2018年3月31日までのデータから最尤推定し(表2)、最終的な予測モデルとした。
なお、システム誤差の分散値が大きいほど対応する変動要因に関する予測の確度が低く、予測から大きく外れる可能性があることを表しており、変動要因選択の妥当性を判断する指標として利用することなどが考えられる。
| vt | 1815.3 |
|---|---|
| wt平日 | 6.6 |
| wt土曜日 | 0.9 |
| wt(日曜・祝日) | 1.1 |
| wt年始営業日 | 16.0 |
| wt年末営業日 | 0.0 |
| wt月末 | 12.1 |
| wt給料日 | 0.3 |
| wt年金支給日 | 0.0 |
| wt連休前日 | 910.5 |
| wt連休翌日 | 0.0 |
4.実験結果
2章で紹介した金融機関からのATM端末関連の問い合わせコール数データについて、3章3節に示したモデルによる予測を行った。ここで、コール数を予測する目的はオペレータのシフトを最適化することであるが、シフトの決定は通常、該当の月の数週間前には行われるため、シフトの検討を始める時点で数週間先のコール数を予測できている必要がある。本稿では、OFEでの運用に合わせ、2カ月先までのコール数予測を行った結果を紹介する。
4.1 2カ月先までの予測結果
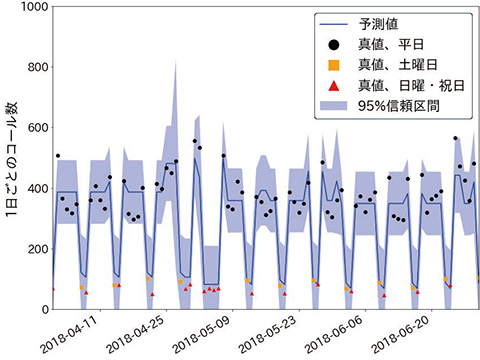
図6に、2018年4月1日から2018年6月30日までの実績コール数と、予測コール数の比較を示す。ここで、予測は1カ月単位で行い、対象月の前々月末日までのデータを基に予測している(例:2018年4月1日~2018年4月30日のコール数予測は2018年2月28日までのデータを基にしている)。表3に示すように、全体の76%が68%信頼区間に、98%が95%信頼区間内に収まっており、妥当な予測結果と考えられる。
動的線型モデルによる予測では、予測値が確率分布の形で得られるため、予測の確実性が低く、誤差が大きくなるリスクが高い場合には予測値の分散が大きくなり、信頼区間が広がるという形で可視化される。今回適用したモデルでは、表2にみられるように連休前日という要因による増減の予測値の分散が大きくなっており、他の日と比べて予測の確度が低くなっていることがわかる。今回のモデルで連休前日の予測確度が低くなっている要因としては、連休前日のサンプルが16件と少なく、外れ値の影響を強く受け、十分に学習できていないことが挙げられる。
| 95%外 | 1日(1.6%) |
|---|---|
| 95%内、68%外 | 14日(22.6%) |
| 68%内 | 47日(75.8%) |
4.2 重回帰モデルによる予測との比較
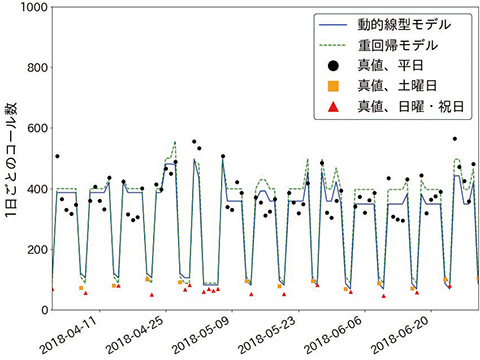
また、ベースラインとして、動的線型モデルで使用したのと同様の変動要因を使った重回帰モデルを作成し、同じデータについての予測結果を比較した。動的線型モデルは分布推定を行っているが、重回帰モデルは点推定を行うモデルであるため、予測の平均のみを用いた比較とした。図7のように、両モデルで概ね近い予測結果になっているが、予測結果と実績値の平均二乗誤差で評価すると、重回帰モデルによる予測では3435.0、動的線型モデルによる予測では2389.9と30%低下しており、点予測のみの精度で見ても重回帰モデルと同等以上の性能を発揮できていることが確認された。
なお、全体として重回帰モデルによる予測では動的線型モデルよりやや大きなコール数が出力されている。これは、動的線型モデルではコール数の平均 θt平日 が逐次的に更新されていくのに対し、重回帰モデルではコール数の平均は固定値として全入力データから推定するという違いが影響している。図1にみられるように、OFEで受信するコール数は2015年ごろから現在までに徐々に減少しているため、全入力データから推定された平均値はコール数が大きい過去のデータに影響され、やや大きい値を取ることになっている。
4.3 コール数予測に基づくオペレータ配置の最適化
コール数を予測する目的は、必要なオペレータ数を算出し人員配置を最適化することである。したがって、予測コール数から算出された必要オペレータ数と、最適なオペレータ数の差の大きさによってコール数予測の有効性を評価した。
OFEでは、受信したコールのうち規定秒数以内に応答できたものの割合をサービス品質指標のひとつとして用いており、必要オペレータ数を算出する際には、この指標が既定の水準を超えるような最小のオペレータ数を求め、このオペレータ数を使用している。この指標は、オペレータ数 N、単位時間あたりの平均コール数 λ、1回のコールにかかる平均時間(通話時間+後処理時間) μ−1 、および前述の規定秒数 AWT( Acceptable Waiting Time)を基に、アーランC式4)を用いて計算される。なお、ここではコールがポアソン到着し、サービス時間が指数分布に従うM/M/C型待ち行列モデルを仮定している。また、実際には時間帯ごとにコール数が変化することを考慮してオペレータ配置に反映する2)が、簡単のため本稿においては1日を通して単位時間当たりの平均コール数が一定であると仮定して計算を行う。
2018年4月、5月、6月の平日(計62日)について、各日の実績コール数により算出した必要オペレータ数を最適オペレータ数とし、予測コール数から算出した必要オペレータ数が最適オペレータ数と比べてどれだけ過不足していたかを表4にまとめた。単純には、表中で色付けしている±0人の行の人数が多く、他の行の人数が少ないほど良い予測といえる。算出に当たって、パラメータ μ−1、 AWT についてはOFEで実際に用いられている値を使用した。
OFEでスタッフが過去の平均コール数を経験と勘を基に補正するという従来通りの方法でコール数を予測し、その値を用いて算出したオペレータ数と、動的線型モデルによる予測コール数から算出したオペレータ数とを比較すると、最適オペレータ数より1人以上過剰になった日数が28日から17日と39%減少しており、1人以上不足した日数も9日から8日とわずかではあるが減少する結果となった。サービス品質を落とすことなく過剰なオペレータ配置のみを減らせており、適切なオペレータ配置が行えているといえる。
また、重回帰モデルによる予測を用いた場合と比較すると、オペレータ数が1人以上過剰になった日数は24日から17日に29%減少している一方、1人以上不足した日数は8日から9日に微増した。この結果から単純に優劣を判断することは難しいものの、少なくとも同等以上によい人員配置を行えていると考えられる。
| 人員過不足 | OFE 算出 | 重回帰モデル | 提案手法 |
|---|---|---|---|
| -2人 | 1日 | 1日 | 1日 |
| -1人 | 9日 | 7日 | 8日 |
| ±0人 | 24日 | 30日 | 36日 |
| +1人 | 26日 | 23日 | 17日 |
| +2人 | 2日 | 1日 | 0日 |
5.むすび
本稿では、動的線型モデルを用いたコール数予測手法を提案した。動的線型モデルは、コール数データの持つゆるやかな変動と特定の条件で起きる特異な変動を柔軟に扱うことができる。
実験では、オムロン フィールドエンジニアリンググループのコールセンターで扱っているATM関連のコール数データについて予測モデルを作成、予測結果を検証した。検証の結果、実績コール数の76%が68%信頼区間に、98%が95%信頼区間内に収まっており、妥当な予測が行えていること、ベースラインとした重回帰モデルによる予測と比べ平均二乗誤差が30%小さく、精度の高い予測ができていること、予測精度の向上が人員の過剰配置を39%抑制する効果につながっていることが確認された。
オムロン フィールドエンジニアリンググループのコールセンターでは、担当者が人手で毎月およそ1日かけて予測とオペレータ配置の検討を行っていた。このプロセスに動的線型モデルによる予測を導入することで、より適切なオペレータ配置が可能になるとともに、作業量を大きく低減させることができる。現在、動的線型モデルによる予測システムのツール化に向け試験導入を行っており、実際に効果が確認されている。
本手法は、コールセンターのコール数に限らず、様々な時系列データの予測に利用することができる。特に、平均が時間と共に変化していくような非定常な時系列に対しては、ARIMA などの一般的な時系列モデルや、重回帰モデルの適用が難しく、本手法による予測が適している。店舗等の来客数や売上、道路等の交通量の時系列など、こうした特徴を備えているデータは多くあると考えられ、そのようなデータの予測にもこの手法を生かしていきたい。
また、今後の課題としては、予測精度を向上させるため、モデルの構造やパラメータ更新手法を見直することや、変動要因の選択を人間の知見を前提とせず、自動抽出を行うような手法5) を検討することなどが挙げられる。
参考文献
- 1)
- Ibrahim, Rouba; Ye, Han; Ecuyer, Pierre L; Shen, Haipeng. Modeling and forecasting call center arrivals: A literature survey and a case study. International Journal of Forecasting. 2016, Vol. 32, No. 3, p. 865-874.
- 2)
- 伊藤稔.コールセンターにおけるインバウンド予測.UNISYS TECHNOLOGY REVIEW. 2005, Vol. 87, p. 293-304.
- 3)
- G. ペトリス,S. ペトローネ,P. カンパニョーリ,和合肇,萩原淳一郎.Rによるベイジアン動的線型モデル.朝倉書店,2013,272p.
- 4)
- Chromy, Erik; Misuth, Tibor; Kavacky, Matej. Erlang C Formula and its Use in the Call Centers. Advances in Electrical and Electronic Engineering. 2011, Vol. 9, No. 1,p. 7-13.
- 5)
- 田原琢士,王軼謳,山浦佑介,大西健司.コールセンターを対象とした業務量予測に関する研究.人工知能学会全国大会論文集.2017,Vol. JSAI2017, p. 1L14.
本文に掲載の商品名は、各社が商標としている場合があります。
















