FAST 3D Object Position and Posture Recognition for Bin Picking
- Bin picking
- 3D recognition
- Alignment
- 3D sensor
- Robotics
In the product assembly process, there is the work of supplying parts randomly stacked in a container to an automated machine. This is called bin picking. In response to the recent shortage of labor at manufacturing sites and the increase in labor costs, automation of this work is required. By realizing bin picking using 3D sensors and industrial robots, it is possible to manufacture a wide variety of products using the same system, and it is possible to reduce the cost and time of the start-up of the production line. At this time, in order to realize the same speed as a human, it is important to have a technology that can recognize the position and posture of a part in a three-dimensional space with high speed and high accuracy. In this paper, we propose a three-dimensional object position and posture recognition technology consisting of a coarse search and fine alignment. In the coarse search, the rough position and posture of the object are estimated at high speed using the PCOF-MOD feature and equilibrium posture search tree. In the fine alignment, high-precision positional and posture estimation is realized by optimizing the three-dimensional space and the two-dimensional space using a depth image and an RGB image. When the proposed method was evaluated, it was confirmed that the estimation accuracy of the position and posture was improved by about twice compared with the conventional method. In addition, it was confirmed that the recognition time using the proposed method was 146.2 ms on average on a computer equipped with an Intel® Core i7-7700 CPU @ 3.60 GHz, and both speed and accuracy were compatible.
1. Introduction
In recent years, manufacturing floors have suffered increasingly serious labor shortages and labor cost surges. Automating human-dependent processes, including assembly, inspection, and material handling, has become a pressing issue. For the parts feeding processes during product assembly, an example of an automated method of parts feeding is to use a dedicated parts-feeding machine called a parts feeder. However, parts feeders are custom-built machines designed for dedicated use for specific parts. Accordingly, these machines must be designed as required by the number of part types, posing the challenge of increased production line start-up costs and person-hours. Another challenge is that part feeders cannot handle large-sized or easily damageable parts and are more limited in the range of manageable parts. Thus, needs exist for automating so-called bin-picking tasks for feeding randomly piled parts of different shapes in containers into automatic machinery. These challenges will be solved if bin picking can be implemented based on 3D sensors and industrial robots.
A typical flow of processes to implement bin picking goes as follows:
- (1)
- Capturing an RGB-D image of a part through a 3D sensor
- (2)
- Matching this image with a 3D CAD-generated model of the part for position-and-posture recognition thereof
- (3)
- Calculating a robot hand position matching the recognition results to ensure the safe grip of the part
- (4)
- Moving the robot to the calculated position to grip the part.
Of these processes, those assigned to a 3D sensor and an image processing controller are (1) to (3). Step (2), object position-and-posture recognition, is particularly important to implement bin picking on a manufacturing floor with human-equivalent performance. In this paper, we propose a high-speed, high-accuracy 3D object position-and-posture recognition technology.
2. Related Works
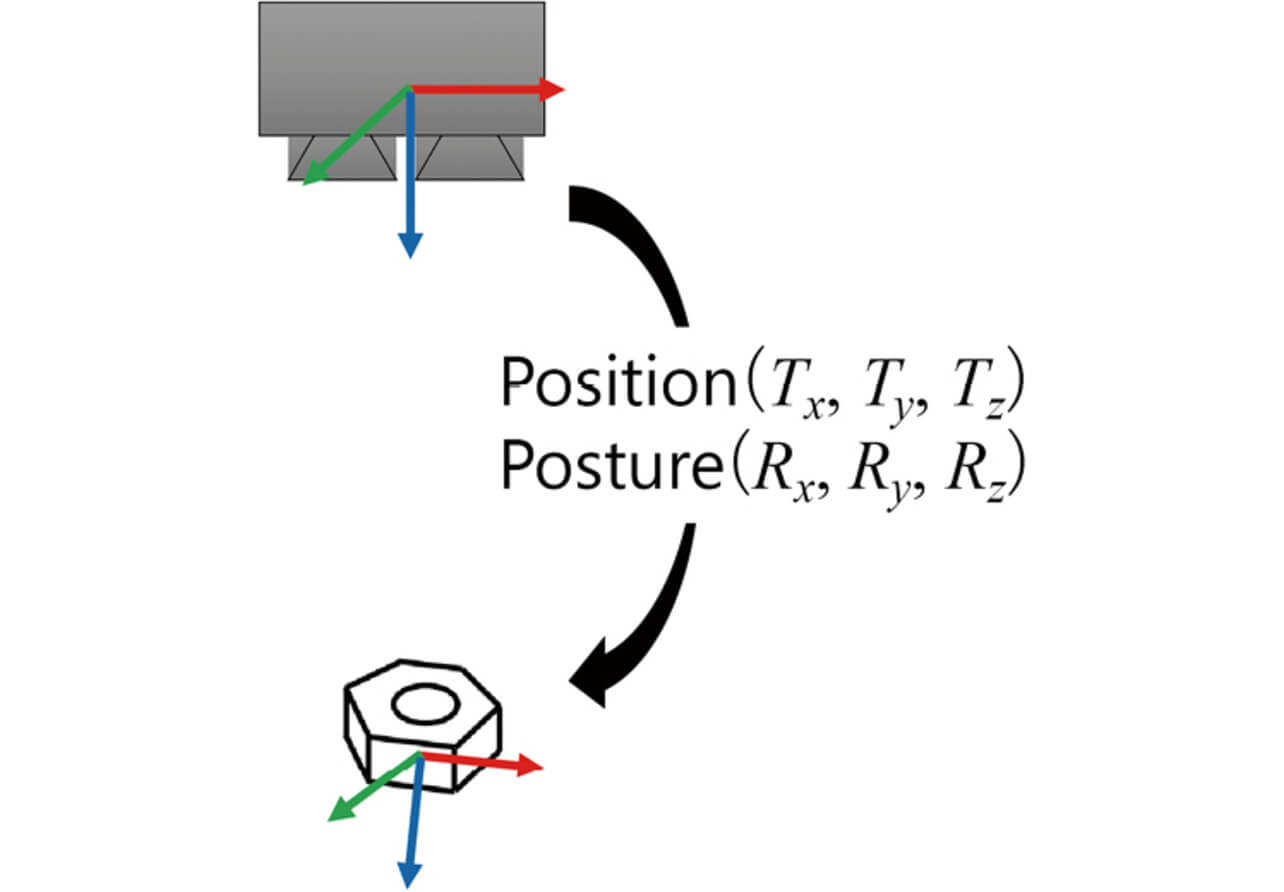
Three-dimensional object position-and-posture recognition is a technology that estimates the 3D-spatial positions and postures (six parameters of translational Tx , Ty , and Tz and rotational Rx , Ry , and Rz ) of parts as viewed from a 3D sensor (Fig. 1). The methods proposed before for 3D object position-and-posture recognition fall largely into either 3D point cloud-based methods1-5) or 2D projection image-based methods6-14).
2.1 3D Point Cloud-based Method
A 3D point cloud-based method matches 3D CAD or otherwise generated models of parts with input data to search positions and postures for high consistency between models and input data. Well-known model generation methods include the following: spin-images1), which describe positional relationships with surrounding point clouds; FPFH2) and SHOT3), which use normal-direction histograms of point clouds around key points; and PPF4,5), which describes two-point relationships. It has been pointed out that these methods have a slow processing speed and exhibit low robustness with an object against a complex background6).
2.2 2D Projection Image-based Method
A 2D projection image-based method uses multi-perspective RGB and depth images of an object to extract its feature quantity values and creates their templates beforehand for matching with newly measured images to estimate the position and posture of the object. Variations of this method include ones that combine local template matching and the Hough Transform7-9) and ones that use templates of whole parts to scan inside images6,10,11). The problem with the former is that they are time-consuming to process most-frequent-value searches from a six-dimensional voting space. The latter methods involve template creation and scanning for objects with variable appearances due to posture changes, and hence their problem is that the processing time increases linearly relative to the number of object types or image resolution. On the other hand, studies have demonstrated that high-speed position-and-posture recognition can be achieved using quantized feature quantity-based tools, such as LINEMOD12), PCOF13), or PCOF-MOD14). PCOF-MOD, in particular, is a feature quantity-based tool using the contour and surface information of parts and has been shown to achieve a higher recognition rate than its alternatives14).
Besides, studies have been conducted to train binary classifiers for object/background distinction to enhance their robustness against complex backgrounds15,16). However, background data collection for each object of interest or each image-capture environment is extremely laborious. Therefore, preferably, models should be created, including templates necessary for object recognition, from 3D CAD models of objects alone.
Based on the above points, we use a template matching-based method as a user-friendly, fast, and accurate 3D object position-and-posture recognition method applicable to real applications on manufacturing floors.
3. 3D Object Position-and-Posture Recognition Method
To implement 3D object position-and-posture recognition, which is both fast and accurate, this study considers a method consisting of a coarse-to-fine search capability to fast search an approximate position of an object and a fine alignment capability for better estimation accuracy. The method adopted here for coarse-to-fine search uses PCOF-MOD (Multimodal Perspectively Cumulated Orientation Feature) feature quantities and BPT (Balanced Pose Tree) from the viewpoint of high-speed processing and recognition rate. For fine alignment, we propose an alignment technique that uses both depth images and RGB images to achieve high position-and-posture estimation accuracy for simple-shape parts encountered on manufacturing floors.
3.1 Coarse-to-Fine Search
In a coarse-to-fine search, a PCOF-MOD feature quantity-based template undergoes a matching process that uses BPT14) to calculate an objectŌĆÖs approximate position and posture at high speed.
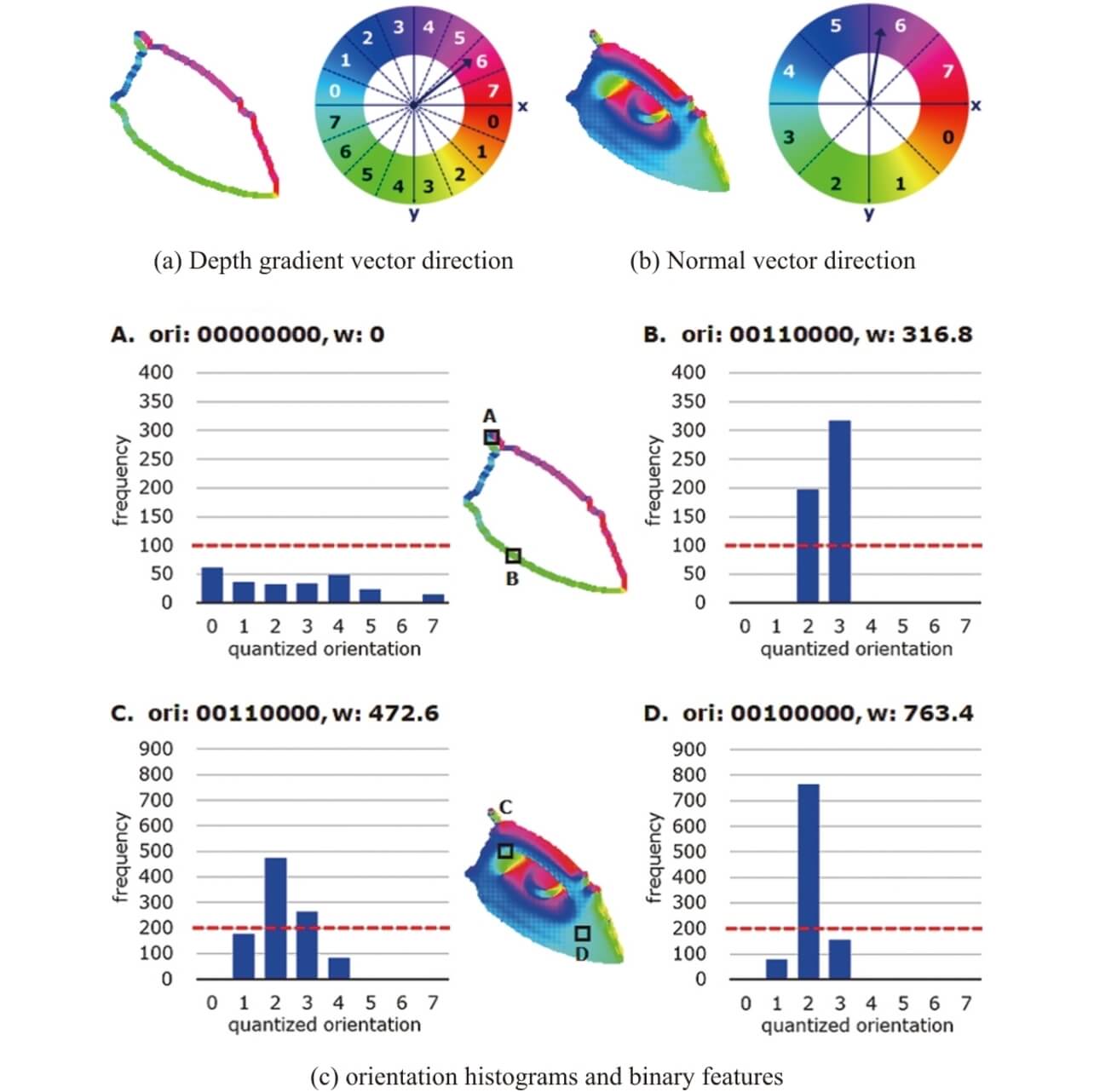
For an object variable in appearance due to pose changes, a PCOF-MOD feature quantity strikes a balance between the objectŌĆÖs acceptable variability in appearance and its robustness against complex backgrounds. In template creation, depth images of an object changing its pose are used to extract the depth gradient vector representing the objectŌĆÖs contour feature and the normal direction vector representing the objectŌĆÖs surface feature. Then, gradient-direction and normal-direction histograms are generated on a pixel-by-pixel basis. For the histograms for each pixel, only the direction at or above the frequency threshold is selected to extract an eight-digit binary number with its corresponding bit set to 1 as a PCOF-MOD feature quantity value (Fig. 2).
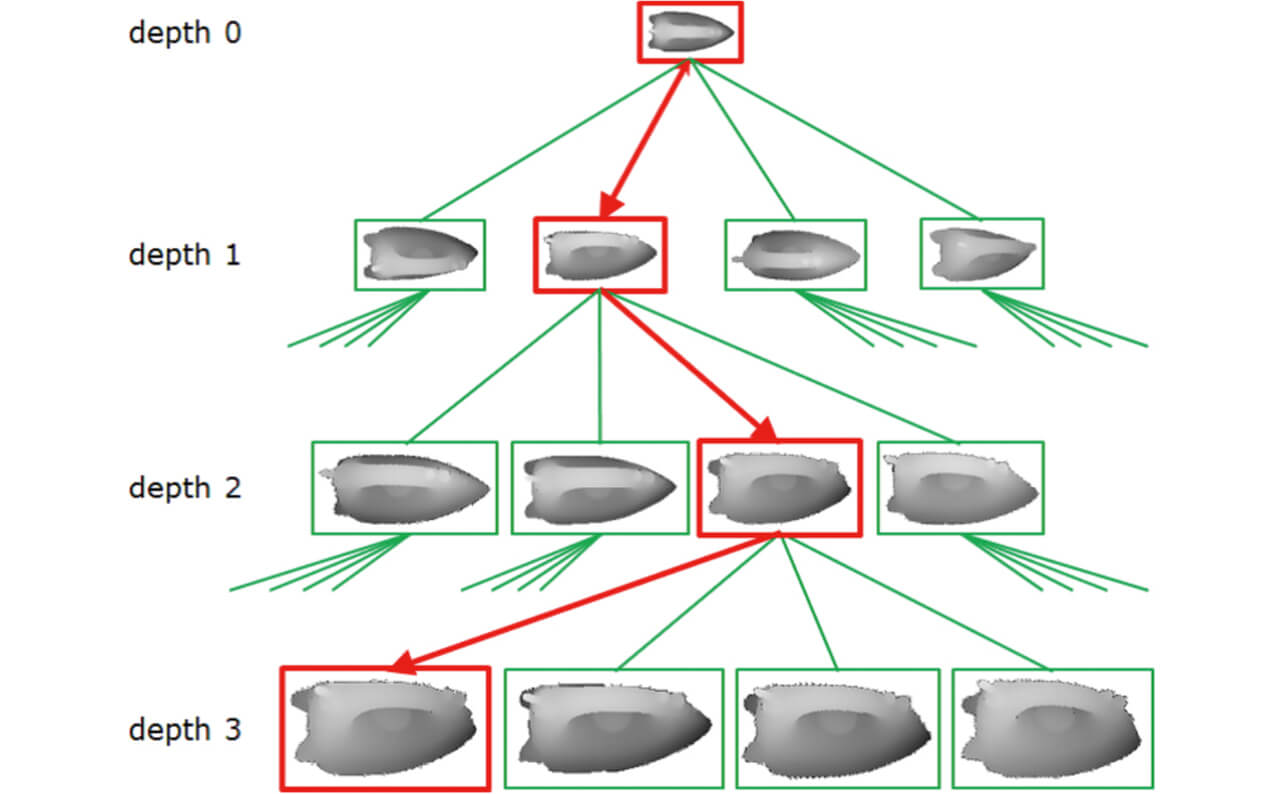
BPT is a search tree consisting of a hierarchy of templates with different resolutions and is configured to make the depths in the hierarchy and the numbers of templates for child nodes linked to parent nodes as uniform as possible to keep the search efficiency uniform between templates. In a matching process, a BPTŌĆÖs parent node template is applied to the tier with the lowest resolution in the image pyramid to scan images and detect candidates. Then, for coordinates with identified candidates, the image pyramid resolution is raised for detailed iterative matching using the child node template to calculate the objectŌĆÖs on-image position at high speed (Fig. 3).
Finally, the correspondence relationship between the three-dimensional coordinates on the 3D CAD model of the object and the two-dimensional coordinates on its input images is used to solve the PnP problem17) to estimate the approximate position and posture of the object.
3.2 Fine Alignment
A position-and-posture estimation made by a coarse-to-fine search is based on 2D projection images and may have low accuracy for the depth-direction position (Tz ) and gradient (Rx , Ry ) that do not show well in changes on the image plane. Accordingly, fine alignment is performed to achieve better position-and-posture estimation accuracy.
Typically, 3D spatial alignment is performed by applying an ICP (Iterative Closest Point) algorithm18) to 3D CAD-generated point clouds and measurement point clouds obtained from depth images. Suppose, however, that simple shape parts consisting of flat surfaces (e.g., the holder in Fig. 7) are randomly piled and in a posture that only allows partial visual access to its surfaces. In this case, an ICP algorithm dependent only on depth images will have difficulty estimating the amounts of translation (Tx , Ty ) and rotation (Rz ) corresponding to changes on the image plane and have the problem of reduced position-and-posture estimation accuracy. Many simple shape parts encountered on manufacturing floors consist mainly of flat surfaces similar to this holder. Therefore, this subsection proposes a fine alignment method that achieves high position-and-posture estimation accuracy even when only flat surfaces are visible.
RGB-D images used for alignment operations have the following characteristics: RGB images provide high estimation accuracy for the position (Tx , Ty ) and rotation (Rx ) on the image plane. In contrast, depth images give high estimation accuracy for the position (Tz ) and gradient (Rx , Ry ) in the depth direction. Hence, the method proposed herein uses the former and the latter complementarily to achieve better position-and-posture estimation accuracy.
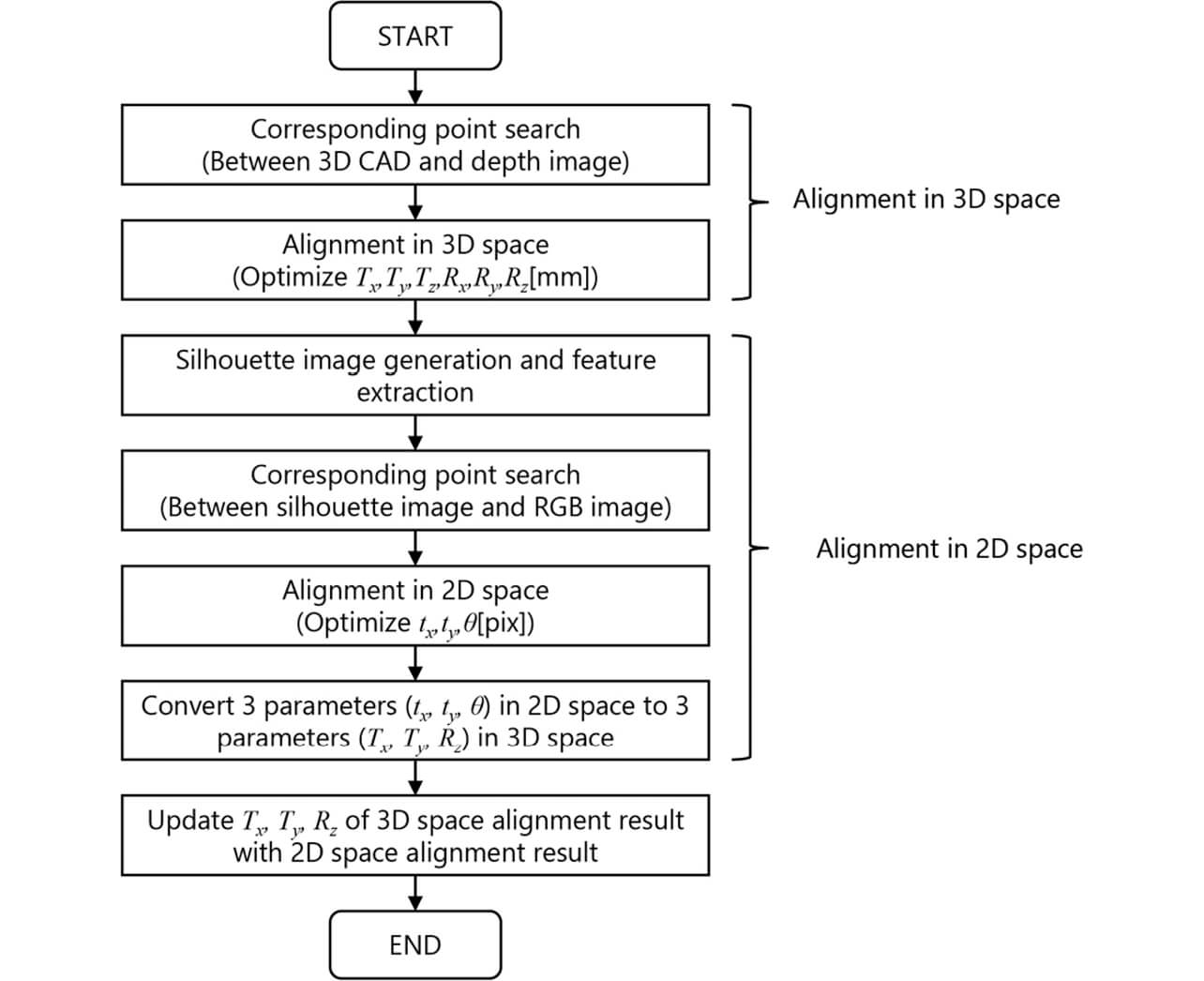
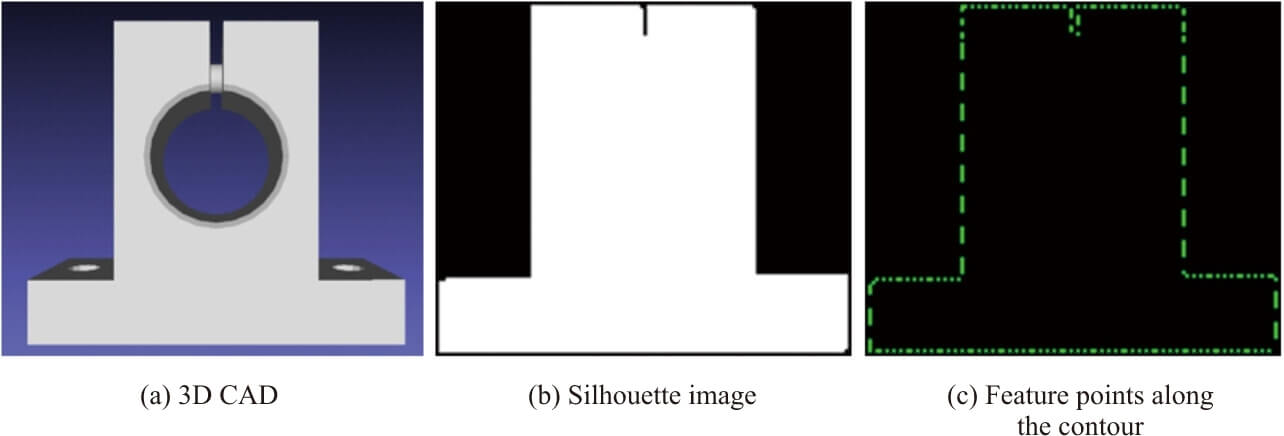
Fig. 4 shows the flow of a fine alignment process using a depth image and an RGB image. This flow aims to perform alignment in 3D and 2D spaces, respectively, and merge their estimation results in the end. First, the position and posture obtained by coarse-to-fine search, the point clouds on the 3D CAD model generated beforehand during template creation, and the measurement point clouds on the depth image are used as inputs for the ICP algorithm to perform alignment in 3D space. Next, a silhouette image is created of an image-plane projection of the 3D CAD model based on the position and posture calculated by ICP in 3D space. The image thus obtained undergoes edge extraction by a Sobel filter to calculate feature points along the contour (Fig. 5). Then, an image obtained by similar edge extraction from the RGB image has its feature points superposed on those in the silhouette image to search the RGB image for edge features close to the feature points to calculate the correspondence relationship between the feature points. Based on this correspondence relationship, ICP is performed in 2D space to estimate the translational tx and ty and the rotational θ on the image plane and solve the PnP problem, thereby determining an optimized set of Tx , Ty , and Rz on the image plane. Finally, these Tx , Ty , and Rz replace their counterparts in the position and posture calculated by ICP in 3D space, optimizing the position and posture in 3D and 2D spaces.
4. Evaluation Experiments
Assuming a gripping task for an industrial robot on the manufacturing floor, a position-and-posture estimation accuracy evaluation (Experiment 1) based on linearity evaluation datasets was performed, followed by a recognition rate/processing time evaluation (Experiment 2) based on randomly piled parts datasets to verify the effectiveness of the proposed method. A prototype of the Omron-developed 3D sensor Model FH-SMDA-GS050B (Fig. 6) was used to capture grayscale and depth images for the datasets. The processing time was measured using a computer with an Intel(R) Core i7-7700 CPU @3.60GHz.

4.1 Experiment 1 Position-and-Posture Estimation Accuracy Evaluation
Experiment 1 evaluated the proposed method regarding static repeatability and linearity accuracy to evaluate its effectiveness for position-and-posture estimation accuracy. The datasets used for static repeatability evaluation were obtained as follows: the 3D sensor was kept in a fixed position relative to three different types of parts consisting of flat and curved surfaces (Fig. 7). Then, the posture with the 3D sensor facing opposite each part was used as the reference for three postures (no gradient, Y-axial gradient only, and X- and Y-axial gradients) to capture 50 serial measurement data images.

For the six parameters of estimated positions and postures, standard deviations were calculated to evaluate the position and posture of the part for shifts.
The image capture method used to obtain the datasets for linearity evaluation was as follows: each part was placed on the X-stage and moved by a predetermined distance for each measurement. Three different 3D sensor poses and two part-moving directions (laterally and diagonally across images) were used to capture 100 measurement data images of each part, with its position shifted in 2-mm increments per shot.
The linearity evaluation proceeded as follows: the estimated positions and postures served as the basis for calculating the distances from the 3D sensorŌĆÖs origin to the eight vertices of thecircumscribed cube of each part and the inter-data differences between the eight verticesŌĆÖ shifts and the stageŌĆÖs shift to evaluate the position-and-posture estimation results regarding linearity.
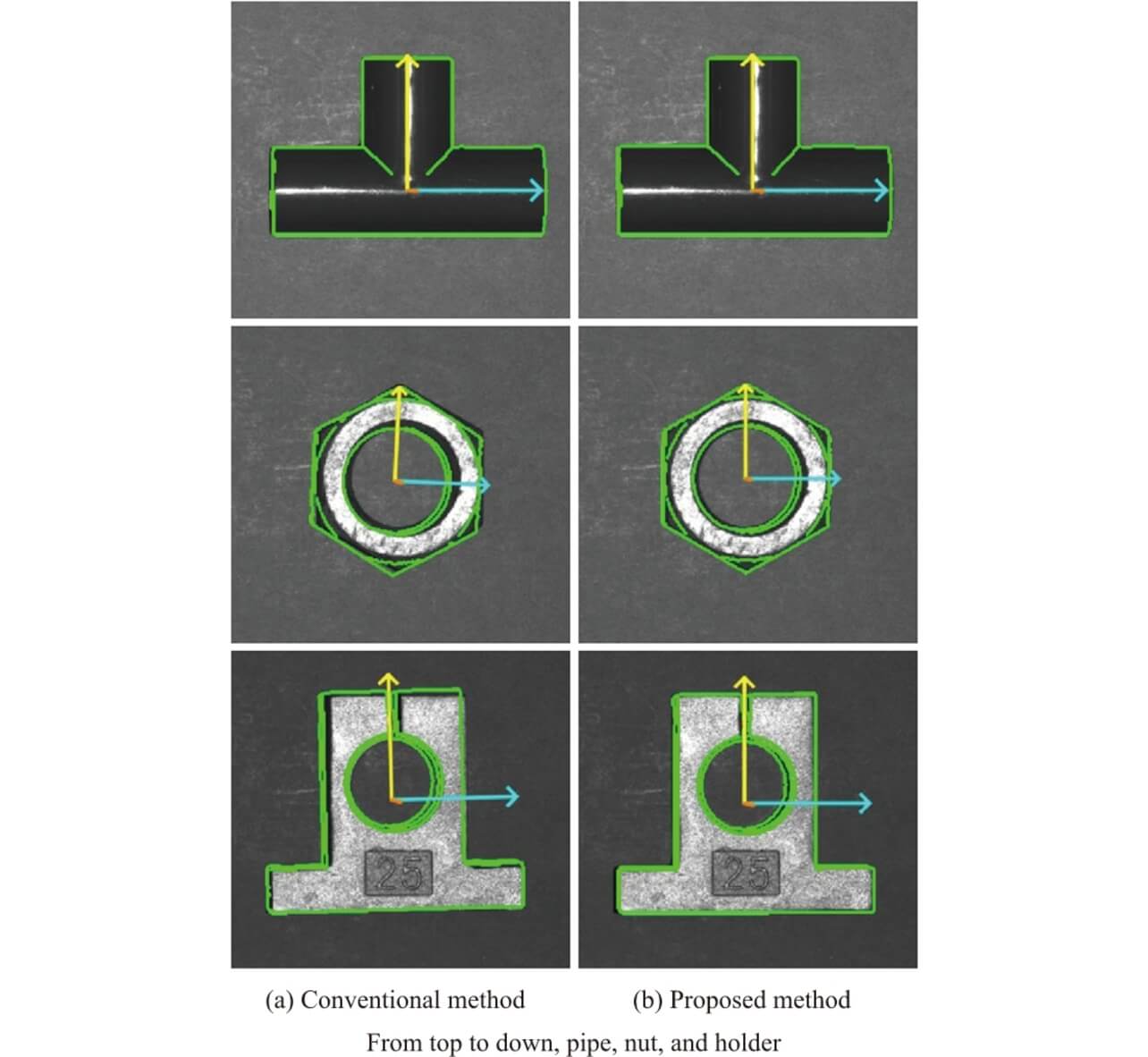
A performance comparison was made between the proposed method and the conventional method14), which performs fine alignment using depth images exclusively after coarse-to-fine search using PCOF-MOD feature quantity values and BPT. Tables 1 and 2 show the static repeatability evaluation results, while Table 3 shows the linearity evaluation results. Fig. 8 shows typical recognition result images obtained by the conventional and proposed methods. The evaluations reveal that the alignment accuracy was improved approximately twice on average compared with that achieved with the conventional method. The proposed method showed significant improvement effects, especially when applied to three-dimensional geometric feature-poor parts, such as nuts or holders, with only some of their flat surfaces visible from certain viewpoints. The alignment result images in Fig. 8 confirm that the proposed method improved the translational or rotational shifts in the image plane direction observed with the conventional method.
| Part | Conventional method | Proposed method |
|---|---|---|
| Pipe | 0.028 | 0.023 |
| Nut | 0.207 | 0.065 |
| Holder | 0.116 | 0.064 |
| Average | 0.117 | 0.051 |
| Part | Conventional method | Proposed method |
|---|---|---|
| Pipe | 0.027 | 0.036 |
| Nut | 0.386 | 0.239 |
| Holder | 0.101 | 0.067 |
| Average | 0.171 | 0.114 |
| Part | Conventional method | Proposed method |
|---|---|---|
| Pipe | 0.054 | 0.074 |
| Nut | 0.687 | 0.164 |
| Holder | 0.712 | 0.250 |
| Average | 0.485 | 0.162 |
4.2 Experiment 2 Recognition Performance Evaluation
In Experiment 2, to verify that fine alignment using the proposed method would not result in a significantly reduced recognition rate or processing speed, datasets were created for six different types of parts containing flat and curved surfaces and randomly piled in containers (Fig. 9) to evaluate the recognition rate and the processing time. The datasets were obtained by capturing 20 measurement data images per part type while changing the randomly piled conditions of the parts. For the exposed parts on top of the random pile in each data image, visually obtained initial position-and-posture input and ICP-based alignment were combined to calculate the true position and posture values for the dataset. Each image shows five to ten parts lying exposed on the top of the pile. Parts subject to recognition were those with a hidden surface area accounting for 15% or less of their whole area. The evaluation sample size per part type ranged from 100 to 200 approximately.

The proposed method was compared with two alternative methods. One was the conventional method14), which performs fine alignment using depth images exclusively after coarse-to-fine search using PCOF-MOD feature quantity values and BPT. The other was a method based on PPF (Point-Pair Feature) and Hough Transform4), which creates model data necessary for position-and-posture recognition, using exclusively 3D CAD, similar to the proposed method. The PPF implementation used was the surface-based matching function included in the HALCON13 commercial machine vision library. The target recognition range was limited to the inside of the container (approximately 700├Ś400 pixels per image). Regarding recognition performance evaluation, precision, recall, and F-score values were calculated based on the absolute error values between the estimated and true position and posture values. Considering that true-value entry to the random-pile datasets was manually performed, the reference thresholds for successful recognition were defined as 5 mm or less for translation and 7.5┬░ or less for the rotational angle. For each part type and all part types combined, Table 4 shows the average F-scores, while Table 5 shows the average processing times.
| Part | PPF | Conventional method | Proposed method |
|---|---|---|---|
| Pipe | 0.825 | 0.942 | 0.946 |
| Ring | 0.754 | 0.977 | 0.967 |
| Link | 0.355 | 0.915 | 0.908 |
| Nut | 0.819 | 0.981 | 0.981 |
| Metal sheet | 0.572 | 0.888 | 0.879 |
| Holder | 0.908 | 0.989 | 0.989 |
| Average | 0.706 | 0.949 | 0.945 |
| Part | PPF | Conventional method | Proposed method |
|---|---|---|---|
| Pipe | 1423.9 | 92.1 | 112.2 |
| Ring | 1736.2 | 106.0 | 129.1 |
| Link | 1066.2 | 186.6 | 204.2 |
| Nut | 1883.4 | 118.1 | 134.9 |
| Metal sheet | 2376.7 | 171.0 | 192.1 |
| Holder | 591.8 | 97.5 | 104.7 |
| Average | 1513.0 | 128.5 | 146.2 |
The evaluation results show that the proposed method matches the recognition rate of the conventional method. Regarding the processing time, the conventional method is approximately 18 ms slower than the proposed method, which remains within a practically acceptable range, considering that a difference of several tens of ms does not matter in a bin-picking application.
5. Conclusions
In this paper, we proposed a 3D-spatial position-and-posture estimation method for various parts to achieve automated parts feeding on manufacturing floors. PCOF-MOD feature quantity values and BPT were used for coarse-to-fine searches to perform high-speed estimation of the approximate positions and postures of the objects. For fine alignment, depth and RGB images were used in pairs to achieve high estimation accuracy. Evaluation datasets were developed to evaluate the performance of the proposed method. The proposed method showed approximately twice better position-and-posture estimation accuracy than the conventional method.
Future work in position-and-posture recognition may include such improvements as additional feature quantities to enable parts picking, with parts identification included, from a randomly piled heap of similar parts in similar shapes but with subtle differences in some geometric details.
References
- 1’╝ē
- A. Johnson and M. Hebert, ŌĆ£Using Spin Images for Efficient Object Recognition in Cluttered 3D Scenes,ŌĆØ IEEE Trans. Pattern Anal. Mach. Intell., vol. 21, pp. 433-449, 1999.
- 2’╝ē
- R. B. Rusu, N. Blodow, and M. Beets, ŌĆ£Fast Point Feature Histograms (FPFH) for 3D Registration,ŌĆØ in Proc. IEEE Int. Conf. Robot. Automat., 2009, pp. 1848-1853.
- 3’╝ē
- F. Tombari, S. Salti, and L. D. Stefanob, ŌĆ£Unique Signatures of Histograms for Local Surface Description,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2010, pp. 356-369.
- 4’╝ē
- B. Drost, M. Ulrich, N. Navab, and S. Ilic, ŌĆ£Model Globally, Match Locally: Efficient and Robust 3D Object Recognition,ŌĆØ in Proc. IEEE Computer Society Conf. Comput. Vision Pattern Recognit., 2010, pp. 998-1005.
- 5’╝ē
- S. Hinterstoisser, V. Lepetit, N. Rajkumar, and K. Konolige, ŌĆ£Going Further with Point Pair Features,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2016, pp. 834-848.
- 6’╝ē
- S. Hinterstoisser, V. Lepetit, S. Ilic, S. Holzer, G. Bradski, K. Konolige, and N. Navab, ŌĆ£Model Based Training, Detection and Pose Estimation of Texture-Less 3D Objects in Heavily Cluttered Scenes,ŌĆØ in Proc. Asian Conf. Comput. Vision, 2012, pp. 548-562.
- 7’╝ē
- E. Brachmann, A. Krull, F. Michel, S. Gumhold, J. Shotton, and C. Rother, ŌĆ£Learning 6D Object Pose Estimation using 3D Object Coordinates,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2014, p. 536.
- 8’╝ē
- A. Tejani, D. Tang, R. Kouskouridas, and T. K. Kim, ŌĆ£Latent-Class Hough Forests for 3D Object Detection and Pose Estimation,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2014, pp. 462-477.
- 9’╝ē
- W. Kehl, F. Milletari, F. Tombari, S. Ilic, and N. Navab, ŌĆ£Deep Learning of Local RGB-D Patches for 3D Object Detection and 6D Pose Estimation,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2016, pp. 205-220.
- 10’╝ē
- W. Kehl, F. Tombari, N. Navab, S. Ilic, and V. Lepetit, ŌĆ£Hashmod: A Hashing Method for Scalable 3D Object Detection,ŌĆØ in Proc. Brit. Mach. Vision Conf., 2015, pp. 36.1-36.12.
- 11’╝ē
- T. Hodan, X. Zabulis, M. Lourakis, S. Obdrzalek, and J. Matas, ŌĆ£Detection and Fine 3D Pose Estimation of Texture-Less Objects in RGB-D Images,ŌĆØ in Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst., 2015, pp. 4421-4428.
- 12’╝ē
- S. Hinterstoisser, C. Cagniart, S. Ilic, P. Sturm, N. Navab, P. Fua, and V. Lepetit, ŌĆ£Gradient Response Maps for Real-Time Detection of Textureless Objects,ŌĆØ IEEE Trans. Pattern Anal. Mach. Intell., vol. 34, pp. 876-888, 2012.
- 13’╝ē
- Y. Konishi, Y. Hanzawa, M. Kawade, and M. Hashimoto, ŌĆ£Fast 6D Pose Estimation from a Monocular Image Using Hierarchical Pose Tree,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2016, pp. 398-413.
- 14’╝ē
- Y. Konishi, K. Hattori, and M. Hashimoto, ŌĆ£Real-Time 6D Object Pose Estimation on CPU,ŌĆØ in Proc. Int. Conf. Intell. Robot. Syst., 2019, pp. 3451-3458.
- 15’╝ē
- E. Brachmann, F. Michel, A. Krull, M. Y. Yang, S. Gumhold, and C. Rother, ŌĆ£Uncertainty-Driven 6D Pose Estimation of Objects and Scenes from a Single RGB Image,ŌĆØ in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., 2016, pp. 3364-3372.
- 16’╝ē
- R. Rios-Cabrera and T. Tuytelaars, ŌĆ£Discriminatively Trained Templates for 3D Object Detection: A Real Time Scalable Approach,ŌĆØ in Proc. IEEE Int. Conf. Comput. Vision, 2013, pp. 2048-2055.
- 17’╝ē
- R. I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision. Cambridge, UK: Cambridge Univ. Press, 2004.
- 18’╝ē
- S. Rusinkiewicz and M. Levoy, ŌĆ£Efficient Variants of the ICP Algorithm,ŌĆØ in Proc. 3rd Int. Conf., 2001, pp. 145-152.
Intel® Core is the registered trademark of Intel Corporation in the United States and other countries.
The names of products in the text may be trademarks of each company.
















