Optimization of Multi-Channel Lighting by Lighting Simulation for Visual Inspection
- Lighting Optimization
- Visual Inspection
- Multiobjective Optimization
- Lighting Simulation
- Multi-CH Lighting
In an imaging system with multi-CH lighting, this paper addresses the issue of optimizing the lighting conditions and the imaging conditions of the camera so that they are suitable for visual inspections. The proposed method establishes a technique for accurately simulating an image of a workpiece (subject to be inspected) under arbitrary lighting conditions by image synthesis and by correcting the hardware characteristics of ambient light, sensor noise, dark current offset, and the quantization of light intensity. By this technique, the number of photographs required for optimization was reduced to the logarithmic order of the number of patterns to be evaluated, and the search for the optimal solution could be completed in 1-2 seconds (for 39 CHs) from all lighting patterns. In addition, the proposed method works universally with multi-CH lighting devices in an arbitrary configuration, while the conventional technique requires modification of the optimization algorithm depending on the configuration of the lighting device. The proposed lighting simulation is a fundamental technology for automating the teaching process and making it off-site.
1. Introduction
1.1 Background
Visual inspection of products in the manufacturing industry is one of the operations where the replacement of labor by automated machines has not advanced but is the most important challenge of automatization, considering the decreasing working population in the future. In recent years, automatization technology for inspections has advanced significantly owing to the progress of the technologies, such as artificial intelligence, machine learning, and typically deep learning. However, the time consuming operation required in constructing the inspection system for visual inspections and machine vision is generally the design of the imaging system involving optimization of the lighting conditions, and automatization of this operation is not much advanced. When this operation is difficult and is made manually by persons, the steps of manual adjustment of the lighting equipment changing the inspected workpieces one by one so that visual detection of any possible defect of the workpiece that will vary individually can be made without fail, and the step of examination and verification of the inspection algorithm must be repeated, which requires significant person-hours to achieve the desired detection capability.
The difficulty involved in the optimization of lighting conditions is that no expedient method is available to seek the appropriate lighting conditions other than to repeat imaging by changing large numbers of workpieces in the imaging setup, when it is unknown what images can be taken under what lighting conditions. When such restrictions of hardware are imposed, the sufficient number of trials required to obtain the optimum result cannot be made, and the optimum solution cannot be obtained within the allocated person-hours.
The multi-CH lighting optimization technique based on the lighting simulation technique is proposed in this paper to solve this issue. The lighting simulation here means the simulation of the entire imaging system, including the lighting system whose light distribution can be controlled in order to output the presumed image for the given lighting condition and camera setting, in other words, the problem in normal direction. When such a simulation is possible, seeking the most appropriate lighting condition for the inspection becomes possible for evaluating the images taken. The outcomes that such a lighting simulation technique can bring will be as follows.
- (1) The optimization problem involving the imaging system hardware is changed as the numerical computation problem by the PC, and optimization of the lighting suitable for the algorithm and of the algorithm suitable for the lighting condition can be solved simultaneously by the existing numerical optimization technique.
- (2) Because optimization is made directly for a large number of workpieces/variations in transfer actually imaged, a larger number of samples can be looked over, and more appropriate settings can be determined compared with the optimization made manually by persons.
- (3) Optimization of the lighting condition and the inspection algorithm can be made off-site by the PC after initial imaging on-site, and the process does not occupy the resources, such as the inspection device and sample workpieces, in the optimization process.
- (4) When a new variation mode of the workpiece appears and it becomes necessary to reconfigure the inspection process, troublesome verification work involving new imaging using a large number of workpieces already taken can be avoided.
Various lighting systems are considered as the equipment with light distribution control feature, which are classified to multi-CH light and the movable light. The multi-CH light allows individual intensity adjustment of lights but the number of channels becomes too large when the angular resolution is increased; however, its durability is high because no movable parts are used. It allows lighting from the lighting angle where identification of the defect becomes easy and reduction of the texture inappropriate for inspection by simultaneous lighting from different angles. The movable light is a type in which light distribution is changed by moving position of the lights and includes the type where the position of the light is changed manually. The mechanical system to move the lights becomes necessary when the distribution of light needs to be parametrically controlled automatically as a mathematical optimization problem.
The multi-CH lighting is discussed in this paper. The reason is that an accurate lighting simulation can be made by superposition synthesis using simple addition and subtraction of images. Because an accurate lighting simulation is difficult for movable lighting, priority is not given to the study, and it is not discussed in this paper. While the lighting simulation technique discussed in this paper can be applied to any multi-CH lighting independent of the specific system, the lighting systems FL-MD180MC (Fig. 1) and FL-MD90MC having 39CH (13 azimuth angles and 3 colors) for the FH series are used in the experiment.
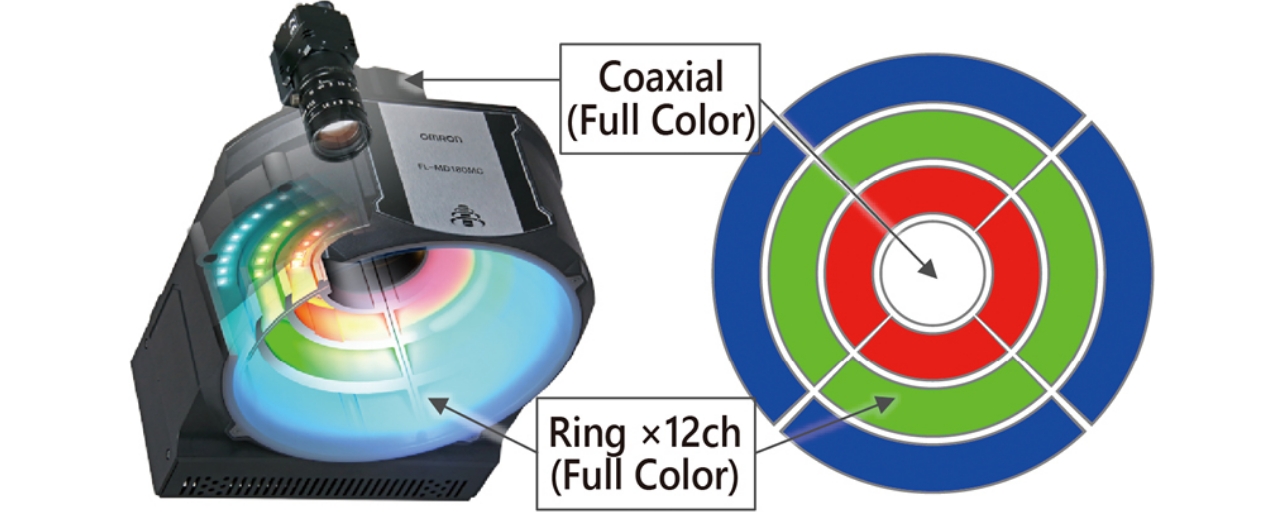
1.2 Related Studies
The method to select the lighting pattern with the highest evaluation index by discriminant analysis actually repeating imaging in various lighting patterns1) is reported as the available technique for this problem. Discriminant analysis is also used for the evaluation index in this paper, but the proposed technique is superior in the following two points.
The first point is the time required for optimization. Let K be the number of lighting channels, T be the number of quantization levels of luminous intensity, and E be the possible number of exposure levels, then the number of lighting conditions becomes E * T K , which increases exponentially with respect to number of channels, and when the number of channels is large, it takes enormous time to take and examine images under all imaging conditions. By the examination in this paper considering such a problem, the number of imaging events can be reduced to multiples of K by the proposed technique. In the conventional technique, the proposal is to solve the problem of too large a number of imaging events by efficient searches using the coarse-to-fine search algorithm1), but it requires the design of the search algorithm empirically every time based on the configuration information of the lighting-CH. The proposed technique in this paper allows the design of the optimization algorithm to be independent of the specific configuration of the lighting-CH and the construction of the algorithm that can be applied generally to any multi-CH lighting system.
Another difference is that it is easy to construct an evaluation function. Because the statistical dispersion of the workpiece is handled generally in a visual inspection, optimization using the evaluation function for multiple samples is required rather than using a single workpiece. Optimization of lighting by any evaluation function using all images of the samples simultaneously becomes possible in the proposed technique. In addition, when the problem setting of the lighting design is a multi-objective optimization problem that requires optimization balancing multiple requirements of the inspection and where a single objective function cannot be defined in advance, the solution must be renewed by interactions modifying the objective function, but by the proposed technique, another imaging event is not required even when the objective function is changed, and a quick response and excellent usability can be realized.
Proxy Modeling2), where behavior of the imaging system is approximated by machine learning, is also examined as optimization of the imaging system using the imaging simulator as in this paper.
1.3 Notation
Bold lowercase letters indicate vectors and bold uppercase letters indicate matrices.
Others are scalar quantities. ||ŌłÖ|| indicates the l2 norm of the vector and 
2. Lighting Simulation by Image Synthesis
It is important that the accurate imaging system simulator be constructed in the optimization of the lighting and imaging systems with control of the degrees of freedom. In this paper, high accuracy of estimation correcting the actual characteristics of the device is realized focusing on the fact that the imaging simulator can be realized by simple image synthesis (superposition of images) in the case of multi-CH lighting.
2.1 Acquisition of Workpiece Evaluation Image by Basis Illumination Pattern
It is assumed that the linearity of the sensor of the imaging system (linearity between intensity and pixel value) exists for the lighting simulation by superposition of images. This means that the system is sufficiently linear, including the signal processing, such as demosaicing of the color filter array, zero pixel value when the intensity is zero by correction of the dark current offset and with the image processing, including HDR (high dynamic range) synthesis, to eliminate nonlinearity due to pixel value saturation. The image taken in such a manner is called the intensity image. Consider the situation where an image of the workpiece illuminated by multi-CH lighting with number of channels K is taken for the inspection, and the relative intensity of the respective channel (intensity that is constant factors of intensity) should be expressed as the following relative intensity vector.

Consider the situation where the optimum lighting condition 

By taking images of the workpiece under such illumination patterns, it becomes possible
to reconstruct the image of the workpiece illuminated by any illumination pattern.
This process is equal to the estimation of the LT (Light Transport) matrix3). It is generally desired to determine the illumination pattern as a rank of the matrix 

When N < K, the degree of freedom by the number of lights cannot be fully utilized, but the time required for imaging of the workpieces can be reduced. Such a situation occurs in the problem setting where control of the degree of freedom K is large. Typical example is the LT matrix estimation method3) using compressed sensing.
The case where N > K can be also considered and it is more than required in the sense of fully utilization of the degree of freedom, and the number of images taken will become useless, but such a case can be used for the purpose of improving the S/N ratio and the dynamic range4).
Let the intensity image taken in the illumination pattern hn be called the basis image. Using the matrix F = [






Where 

Consider that the signs of inequality for the vector and matrix are the signs of inequality
for all of their elements. When 





2.2 Evaluation Formula of Sensor Model and Image Synthesis
The model used to convert the image vector 



In this case, c (1 Ōēż c Ōēż C) is the color index of the color filter of the camera and dc is the dark current offset to be obtained in advance by calibration. When the sensor follows such a model, the lighting simulation by image synthesis under multi-CH lighting is expressed by the following equation.

In this case, 



3. Determination of Optimum Lighting Condition for Inspection
3.1 Evaluation Criteria Cross Entropy vs. S/N
The purpose of lighting design in visual inspections is to allow correct discrimination between quality products and defective products. When the predefined discrimination algorithm is given as the discrimination criteria, the optimization problem of lighting is formulated as the problem of minimizing cross entropy to make discrimination results between the quality and defective products in agreement with the correct answer. When the discriminator is the machine learning device, learning of the optimization of lighting and by the discriminator may be made simultaneously to enable the highest performance of both functions.
However the problem encountered in minimizing cross entropy is that a large number of samples are required that are labeled as quality or defective products. This is a big issue in the start-up period when a large number of samples cannot be obtained. In particular, when optimization of the lighting system with a high degree of freedom is undertaken, the criteria for discriminating the small number of quality/defective product labels will result under any optimum lighting condition (the condition cannot be determined uniquely).
To solve this problem, maximization of the S/N ratio in the sense of dissociating the foreground designated by the user from the background is employed in this paper. This is a method to optimize the lighting using the evaluation criteria for images (contrast, brightness, and proximity) as the basis. When considered as above, the following two requirements mainly apply in the lighting design used for visual inspections.
- (1) To make a feature that allows easy discrimination between the quality and defective products possible (i.e., to make the defect easily visible)
- (2) To make dispersion between the quality products difficult to discriminate
As the above requirements are conflicting requirements in many cases, the design of the lighting system balancing these requirements is the challenge in optimization.
3.2 Acceleration of Evaluation Function in Quadratic Form
As discussed in Subsection 2.2, the basis images are taken with different exposure
times to measure the gradation accurately. For that reason, weighting in image synthesis





The approach to restrict the evaluation function to a quadratic expression is used
to accelerate the evaluation of the image evaluation criteria in this paper. The synthesized
images is expressed as 



As contrast can be expressed as 












As such, the evaluation function allowing accelerated evaluation independent of the number of pixels of the images can be realized by expressing the coefficients of the quadratic expression. Note that these expressions become invalid when pixel saturation occurs. Accordingly, optimization should be made within the range where pixel saturation will not occur, and when saturation is involved, optimization should be made by direct calculation of the l2 norms after clipping of the images by saturation without simplification using a matrix.
3.3 Lighting Design by FisherŌĆÖs Linear Discrimination
FisherŌĆÖs linear discrimination is the method to obtain the projection vector that minimizes dispersion within the class and maximizes dispersion between classes. The effectiveness of this method is limited compared with the method incorporating non-linear computation because the computation to generate the feature vector is simply the inner product. Because optimization of the lighting condition discussed in this paper is simply a computation of the inner product and the linear projection in the mathematical sense when imaging by the multi-CH lighting is regarded as the computation, the use of FisherŌĆÖs linear discrimination to obtain the optimum linear projection is appropriate. The problem to compute the multi-CH light illumination pattern that realizes FisherŌĆÖs linear discrimination is formulated as explained below where dispersion within the class and dispersion between classes are defined focusing on closeness (similarity) of the images by the l2 distance of the images.
The problem to discriminate the workpieces generally into categories of V is considered,
for example, when the workpieces are discriminated into two categories: quality products
and defective products, V = 2. The index of the category 



Consider that the images of the workpiece used for teaching 



Var (S, M ) is the dispersion calculated from the set and the mean M of multi-CH images S and defined as follows. This can be expressed as the quadratic form of the lighting
vector 

Where ŌŖŚ is the Kronecker product and 


Where 



The meaning to restrict the norm of 

The first approach is to solve the optimization problem for the lighting intensity vector with the non-negativity condition. This paper shows that the numerical optimization can be applied for the limited cases.
The second approach is to realize pseudo-negative lighting intensity by dividing the lighting intensity into two sets, one for positive and the other for negative intensity, taking the images for both sets with the absolute value used for the negative intensity, and obtaining the differences between these images by image processing. The equivalent results can be obtained for the results of images taken directly with the eigenvector where the original positive and negative intensity coexist in this approach but taking images after at least twice changing the lighting condition is required. The multi-shot imaging inspection is not discussed in this paper.
3.3.1 Solution by Semidefinite Programming Method
It is explained here that the optimum lighting solution in the optimization problem of FisherŌĆÖs linear discrimination expressed by the following equation can be obtained quickly with the non-negativity condition by the numerical optimizer, when the number of pairs of the foreground and the background defining the S/N ratio to be maximized is one.

In this case, 


This problem is known as Nonconvex-QCQP (Quadratic Constrained Quadratic Programming)
problem that is generally NP-hard, but in this case, semidefinite relaxation5) can be applied, and the solution can be obtained by SDP (Semidefinite Programming).
Specifically, 


In this case, 
















3.3.2 Solution by Multi-objective Optimization
The solution by the SDP explained above can only handle the problem of maximizing the S/N ratio for a pair of a single foreground and background, and the optimization problem containing a quadratic expression that involves the primary term, such as optimization of the brightness, cannot be handled. When multiple S/N ratios for the number of pairs of foregrounds and backgrounds need to be maximized at the same time or when the brightness and contrast are brought close to the desired values, the multi-objective optimization problem must be solved where multiple objective functions are maximized with a balanced approach. To handle such a problem, the weighted sum method6) is used in this paper, where the weighted sum of the individual objective functions is maximized while realizing the appropriate balance between the objective functions adjusting the weighting factor by a large number of trials. Sequential Least Squares Programming (SLSQP) is used for optimization.
4. Evaluation Experiment
4.1 System Configuration
The system configuration used in the evaluation experiment is based on the OMRON image processing system FH series. The multi-CH lighting systems used are the FL-MD180MC and FL-MD90MC, and the cameras used are the FH-SCX12, FH-SMX12, FH-SCX05, and FH-SMX05. The imaging setup is located in a dark room in order to avoid entry of ambient light when basis images are taken. Imaging algorithms by AEC and HDR, dark current offset correction, and calibration function for correction of intensity level - brightness are incorporated as the processing units implemented in FH. Other optimization algorithms and the UI functions run on the PC connected to FH via LAN.
4.2 UI
The teaching UI of the lighting optimization created is shown in Fig. 2. Images of the workpiece are taken after the base level luminescence pattern and imaging method, such as AEC and HDR, are selected in ŌæĀ. The image of the workpiece taken is selected in ŌæĪ, and the evaluation criteria and weighting of the multi-objective optimization are input in Ōæó. In the entry of the evaluation criteria, multiple workpieces can be referenced at the same time. When optimization is executed, the list of solutions is shown in ŌæŻ, and the solution can be compared and examined confirming the evaluation values of the objective functions in Ōæó. When the solution is selected, the intensity level is displayed in Ōæż. Depending on the setting of the problem, one axis of brightness is not determined, and the scales can be adjusted in Ōæź. When the imaging condition is determined, comparison of the workpiece images displayed in Ōæ¦ can be made switching the simulation image and actual image in Ōæ”.
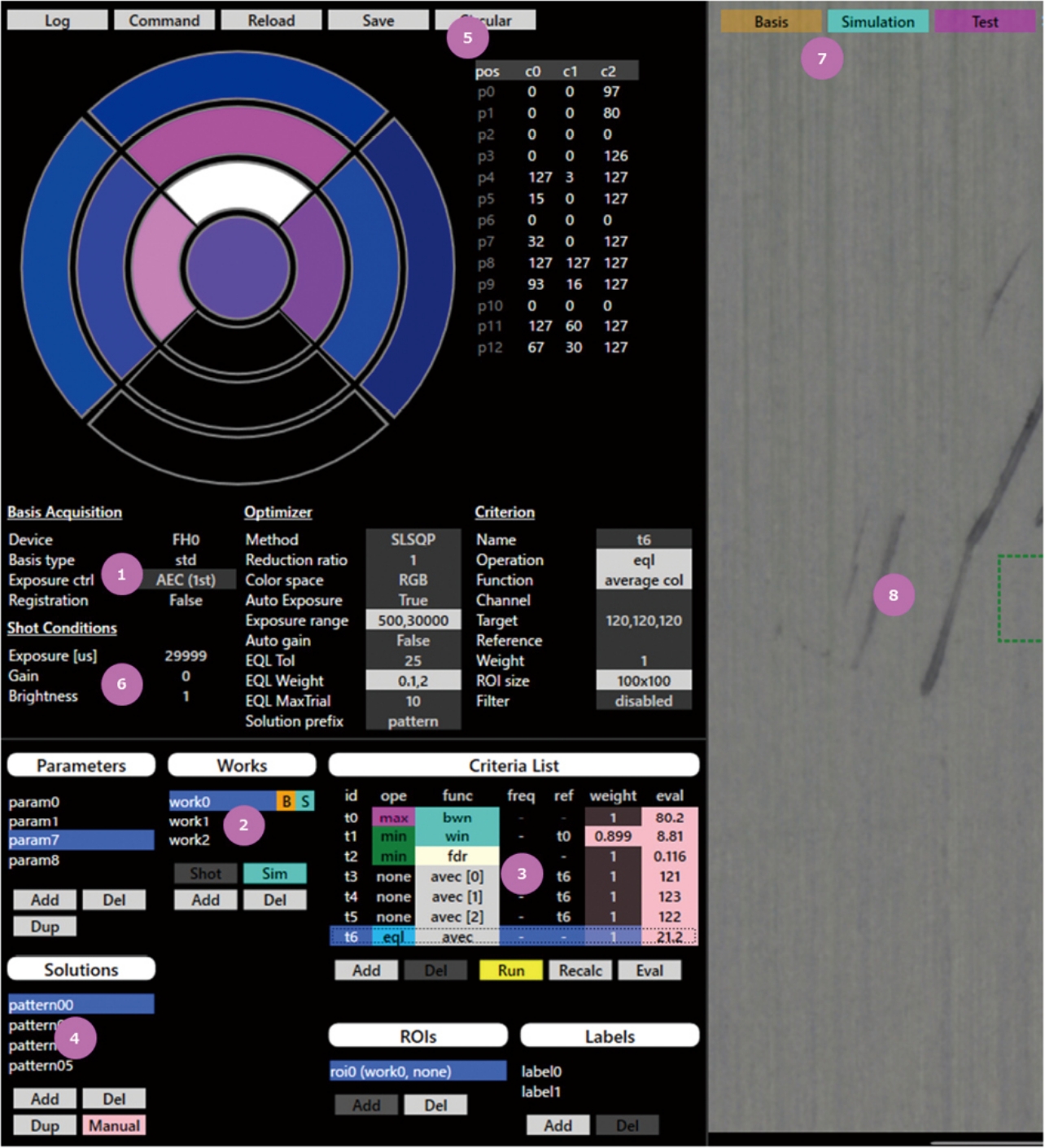
4.3 Installed Software and Execution Time
Python is installed for numerical calculations. Numpy is used for calculation of the matrix, and as computation of the inner product Equation (14) is most time consuming, preprocessing like multi-threading and image shrinkage is applied. For minimization of Equation (18) by SDP, installation of CvxOpt7) is used. The average time required for optimization when N = 39 is 1 to 2 seconds. SLSQP installed in SciPy8) is used for multi-objective optimization. To avoid locally optimized solutions, optimizations are repeated a number of times assigning the initial values N times, and the best solution is selected. The time required is about one second for optimization with the initial value assigned for N times.
4.4 Measures for Entry of Ambient Light
When ambient light other than the light from the lighting equipment enters the image sensor, a difference between the actual image taken and the simulated image will result.
In order to relatively minimize the effect of the ambient light in basis image taking, the technique to always take images with the maximum intensity of lighting and to avoid saturation of the sensor adjusting exposure level of the camera is introduced (AEC imaging).
As another measure for ambient light, the correction process is established where the image under the ambient light is taken with all the lighting devices turned off while the basis image of the workpiece is taken because the presence of ambient light is equal to the situation where one lighting device of the multi-CH lighting stays on. It is confirmed that correction of ambient lighting is possible to the level acceptable in an indoor environment. For verification of the simulation performance in a condition unaffected by ambient light, the result of images of the workpiece taken in the dark room is discussed in this paper.
4.5 Comparison of Images Actually Taken and by Simulation
Fig. 3 shows comparison between the image synthesis simulation results and the actual images for variety of workpieces and illumination pattern.
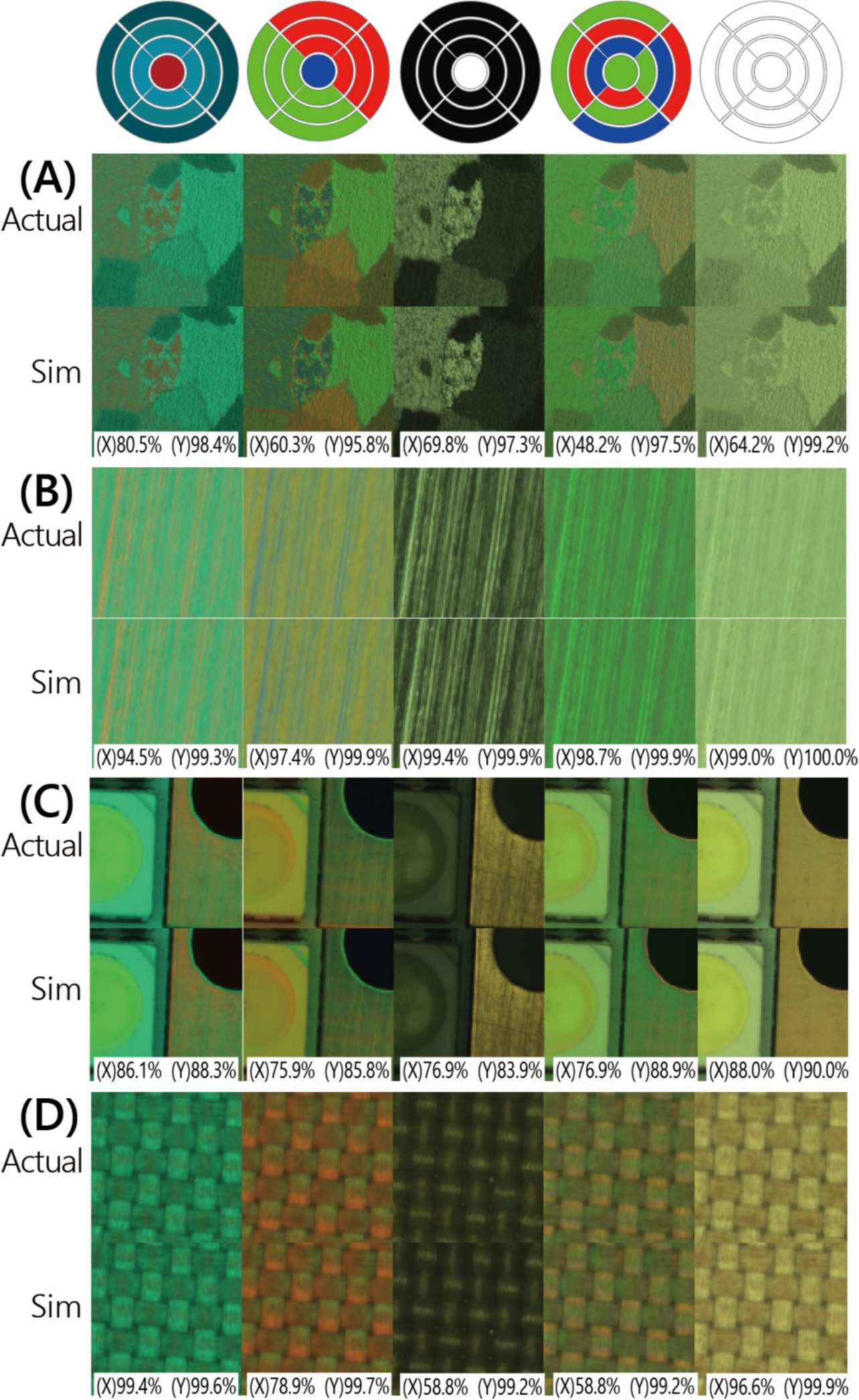
Although it is difficult to identify the difference when both images are closely placed, there is a shift of about ┬▒0.1 in brightness and a color phase shift (shift of brightness by color and by channel). The shift of brightness is caused by the characteristics of the power supply, and the color phase shift is caused by the shift in the estimation of the dark current offset amplified by exposure conversion in AEC imaging. Although improvement by correction is considered possible, it is not considered for the application of optimization of the lighting because the performance at present is satisfactory.
(X) in the figure shows that the ratio of pixel values of the simulation image is within the range of 3Žā of the shot noise of 20 actual images when the shift in brightness is corrected ideally, and similarly, (Y) shows the ratio of pixel values when the color phase shift is ideally corrected. It is shown that an estimation is possible in most cases within the range of shot noise when these are corrected. The reason why the ratios of (X) and (Y) are low for the workpiece (C) is the effect of the noise in dark areas because of the wide brightness dynamic range.
Another noteworthy disagreement is a certain difference in the degree of white blotting near saturation as shown in the Fig. 4. When the pixel saturates, gradation information is lost due to nonlinear characteristics. Accordingly, when interpolation by demosaicing is applied between the saturated pixels, it will create disagreement between the actual image and the image synthesis. Such phenomenon will appear as disagreement in the degree of white blot near saturation region but it cannot be corrected because it is a theoretical phenomenon.

4.6 Optimization Assigning S/N Ratio
Define the S/N ratio of the foreground and background by Equations (10), (11), and (15), and let
Dwithin be defined as the dispersion of multiple backgrounds and Dbetween as the distance between the defect and the background. Introduce the parameter ╬▒ that indicates the degree of image background removal so that optimization becomes
possible with different S/N ratios assigned, and it is re-defined as Dwithin = 

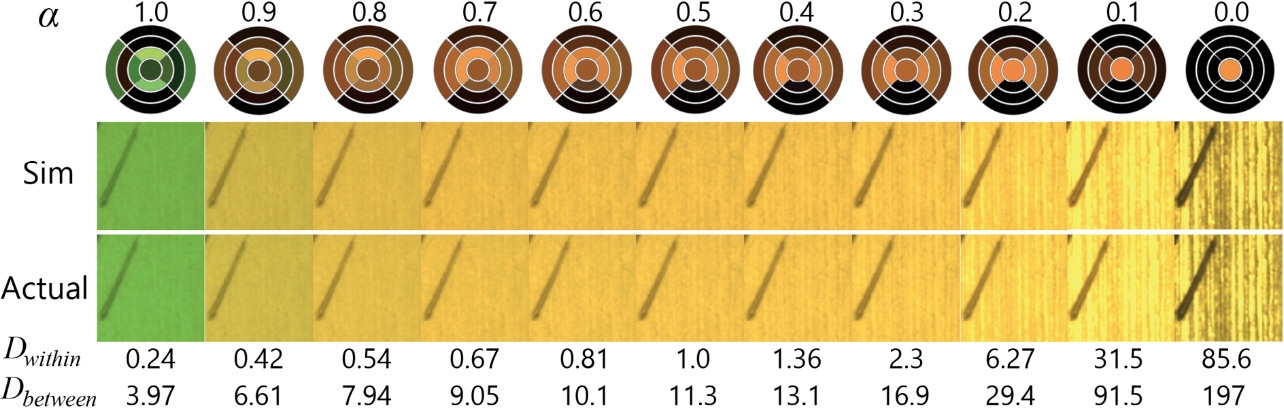
The reason why the lighting color changes when ╬▒=1.0 is that more favorable color is selected to make the background flat in the sense of the l2 distance involving the color channel of the image.
The contrast of the hairline finish of this workpiece is mostly determined by the
intensity ratio balance of the coaxial light (center) and ring light (circumference).
When the contrast is increased, only the coaxial light tends to be selected, and when
the contrast is decreased, both the coaxial light and ring light are used. When value
╬▒ increases, the lighting pattern becomes complicated, but it is possible to find a
simpler lighting pattern with similar performance to these. The reason is that matrix


4.7 Optimization Involving the Pixel Value (Brightness)
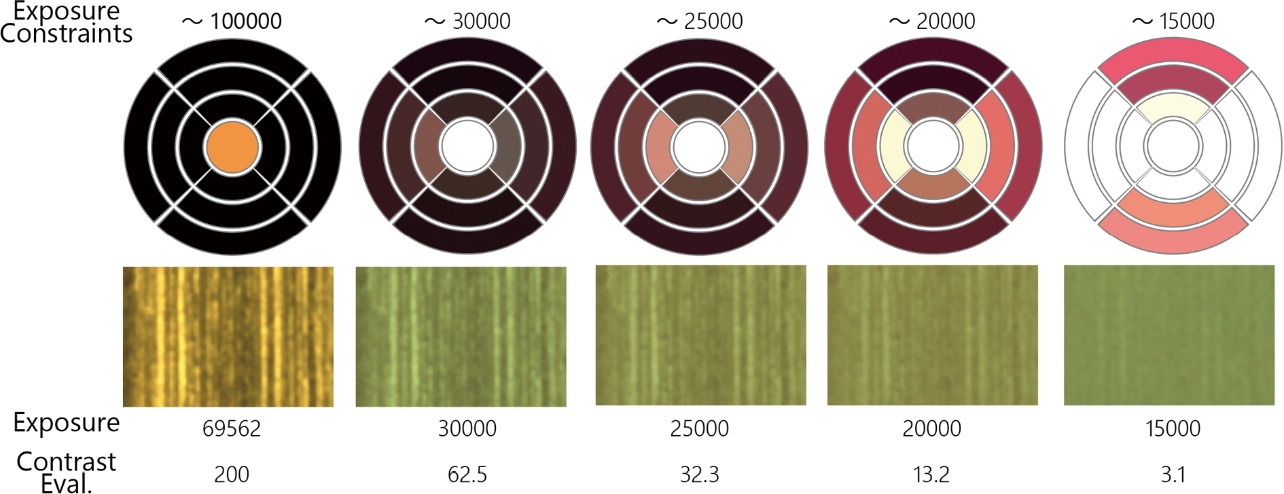
Fig. 6 shows the example where optimization is made to maximize contrast by multi-objective optimization specifying the pixel value (brightness). As the coaxial light provides the highest contrast in the case of a hairline finished metal surface, only the coaxial light is selected in the left column where constraints in exposure is lowest. The constraints of the exposure time gradually increase towards the right and intensity of illumination decreases accordingly when only the coaxial light is used, which will make the specified pixel value unattainable. Accordingly, optimization is made to maximize brightness by illuminating multiple lights at the same time, and as a result, it is confirmed that contrast is sacrificed. This means that the lighting is optimized to maximize the contrast within the range where the specified brightness is produced. This is the advantage of this technique to obtain optimum lighting by image synthesis overlooking the tradeoff between the exposure level and contrast only by numerical computation in multi-objective optimization.
5. Conclusions
The lighting simulation technique using image synthesis for the optimization problem of the multi-CH lighting system for visual inspections is proposed in this paper. It is demonstrated that this technique enables accurate lighting simulation reducing the number of required images taken for optimization exponentially to the logarithmic order of the number of evaluation patterns. The proposed technique is the basic technique that realizes automatized and off-site teaching operations that include the inspection parameter setting.
The authors considered expanding this technique to the simultaneous optimization, including multi-shot imaging inspection and a subsequent inspection, improving usability in multi-objective optimization, and handling of dispersion outside of the sample range by optimization of lighting using simulations of workpiece dispersion.
References
- 1’╝ē
- S. Hayashi, ŌĆ£Fast and automatic lighting parameters determination technology for visual inspection,ŌĆØ (in Japanese), OMRON TECHNICS, vol. 52, no. 1, pp. 30-34, 2020.
- 2’╝ē
- E. Tseng, F. Yu, Y. Yang, F. Mannan, K. S. Arnaud, D. Nowrouzezahrai, J. F. Lalonde, and F. Heide, ŌĆ£Hyperparameter optimization in blackbox image processing using differentiable proxies,ŌĆØ ACM Trans. Graphics (TOG), vol. 38, no. 4, 2019, Art. no. 27.
- 3’╝ē
- N. Chiba and K. Hashimoto, ŌĆ£Sparse estimation of light transport matrix under saturated condition,ŌĆØ in The 29th British Machine Vision Conf. (BMVC2018), 2018.
- 4’╝ē
- Y. Y. Schechner, S. K. Nayar, and P. N. Belhumeur, ŌĆ£Multiplexing for optimal lighting,ŌĆØ IEEE Trans. Pattern Anal. Mach. Intell., vol. 29, no. 8, pp. 1339-1354, 2007.
- 5’╝ē
- Z. Luo, W. Ma, A. M. So, Y. Ye, and S. Zhang, ŌĆ£Semidefinite relaxation of quadratic optimization problems,ŌĆØ in IEEE Signal Proc. Mag., 2010, vol. 27, no. 3, pp. 20-34.
- 6’╝ē
- K. Miettinen, Nonlinear Multi-objective Optimization. Boston, MA: Springer, 1999, p.78-84.
- 7’╝ē
- M. S. Andersen, J. Dahl, Z. Liu, and L. Vandenberghe, ŌĆ£Interior-point methods for large-scale cone programming,ŌĆØ in Optimization for Machine Learning, S. Sra, S. Nowozin, and S. J. Wright Eds. Cambridge, MA, USA: MIT Press, 2012, p. 55-83.
- 8’╝ē
- E. Jones, T. Oliphant, P. Peterson et al., SciPy: Open source scientific tools for Python. 2001. http://www.scipy.org/ (accessed Feb. 1, 2020)’╝Ä
The names of products in the text may be the trademarks of each company.
















