Innovation of the Method for Balancing Trade-off Requirements in the Product Design Process
- Design Optimization
- CAE application technology
- Trade-off balancing
- Design quality improvement
- Design knowledge formalization
One of the common subjects among the product development is the excess of development lead-time and cost, and the degradation of the products due to the redesign work by the problems that occurred at later parts of the product development process. There are various problems, but in this paper, the problem caused by the risks of the unbalanced trade-off between key requirements is targeted for a solution. As the solution, the design optimization method is applied to realize the trade-off balancing design method. The trial was held on the real trade-off design theme, and as the result, 1800 designs were comprehensively evaluated in two weeks by automatic computer calculation. From those designs, the optimally balanced design that exceeded the performance of the conventional product was found. And as the result, the realization of the trade-off balancing design and the possibility of finding the optimal design, which was hardly found by the conventional design method based on experience and intuition, were confirmed.
1. Introduction
One of the common subjects among the product development is the excess of development lead-time and cost, and the degradation of the products due to the redesign work by the problems that occurred at later parts of the product development process. There are various reasons but the one caused by the risk of unbalanced trade-off between key requirements is considered as the major problem1) .
Two factors seem to be in the background. The first factor is that product performance and function are rapidly enhancing in recent years. As the result, manufacturers are forced to design their product with emerging technologies, at narrow design flexibility, and at tightly restricted conditions. So far, manufacturers have overcome by dividing their design forces into individual technical units (e.g., mechanical, electrical, and software) and refining each design capabilities. Although, the changes of the organization have led the miscoordination between the technical units1) .
The second factor is the increasing difficulty of obtaining enough development resources (such as lead-time, man-hours, and costs). Formerly, design evaluations were sufficiently performed even by the hand calculation and the experiments by real prototypes. But, in recent years, technical elements and design parameters, those required to be considered, have increased to overload conventional design methods and became the major reason to degrade the design quality1) .
Recent years have seen significant advances in computerized design verification technologies, such as computer-aided engineering (CAE). Followed by the technologies, the complex and difficult manual calculations became easily performed without real prototypes and at high speed. And further application is emerging to assist designers╩╝ creativity and decision based on their prospects, know-hows, experiences. Computers gather the results of CAE and analyze the data to derive the optimal design values considering multiple design requirements (hereafter, such methods are called ŌĆ£design optimization methodsŌĆØ)2) . But, the application of these new technologies to actual product design processes relies on the manual operation of the designers.
In this paper, instead of designers, we utilized the computer to interface between CAE and a design optimization method to automatically derive the design candidates those satisfy multiple design requirements of actual design problems. And, this new approach is challenged at practical application, and the effectiveness and efficiency are discussed.
2. Design optimization method
Fig.1 shows the whole picture of the design optimization method considered in this paper. What characterizes our method is that a computer performs a series of tasks and judgements those were conventionally done by designer. First, the designer enters to the computer the objective functions, input variables, and design methods and tools (see Fig.1 for the definitions of these terms). In particular, the design methods are a sequence of calculations, verifications, and other tasks and then makes judgements on the qualification to satisfy multiple design requirements. This process is programmed as shown in the right part of Fig. 1 to be performed by the computer.
The output of this method is a list of design candidates those satisfy the design requirements. From this list, the designer selects the best design (hereafter ŌĆ£optimal solutionŌĆØ). The key point of this method is to make the computer automatically run and repeat the design candidate extraction and CAE verification processes shown in the figure. This automated process corresponds to trial-and-error activities the designer used to perform through many working hypotheses and experiments to pursue better design values.
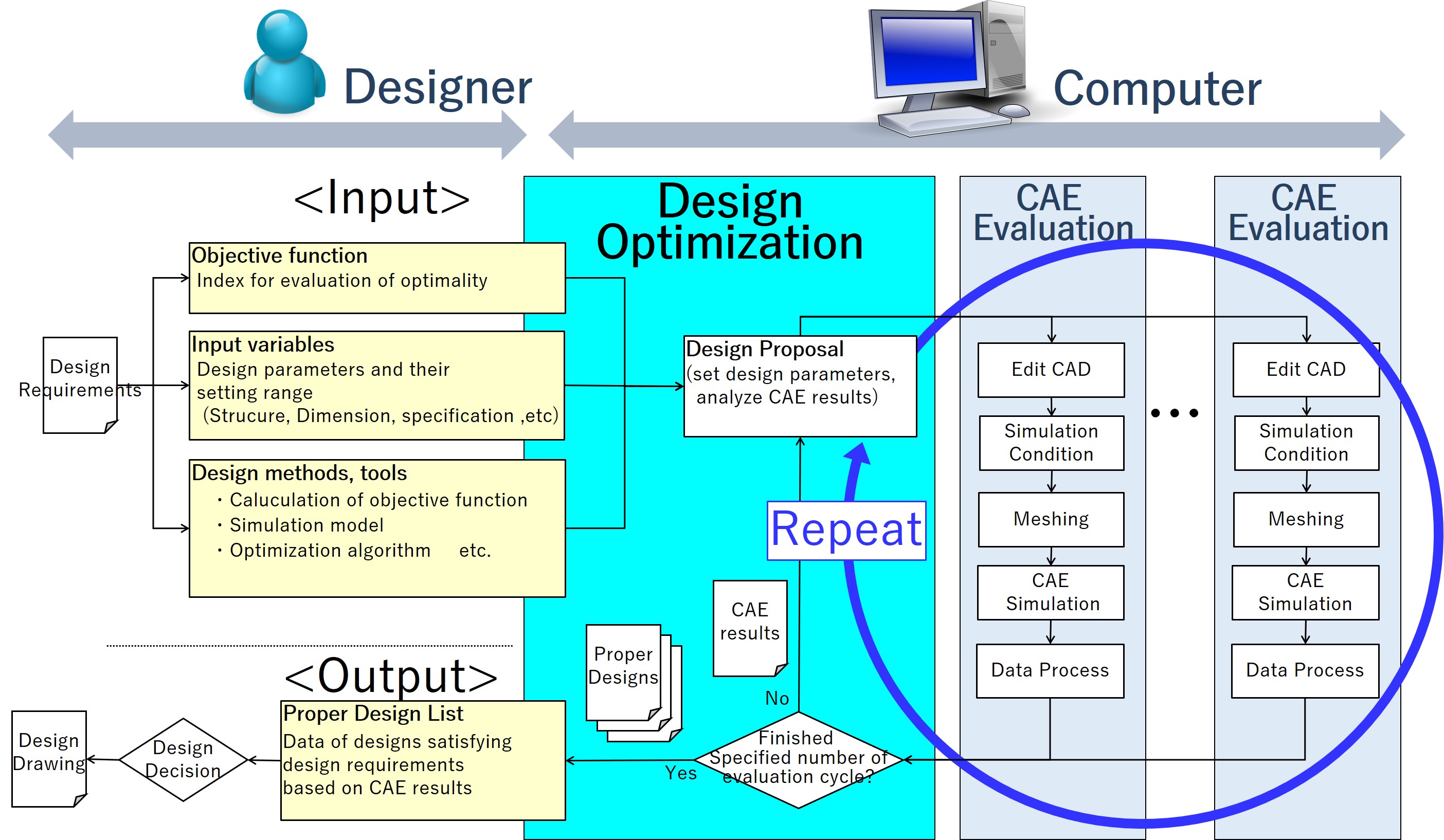
2.1ŃĆĆŌĆ£Design candidate extractionŌĆØ process
Conventionally, a designer examined different design candidates by making full use of the design techniques and know-how built through experience in many design opportunities. To extract design candidates, however, a computer with no design experience must be able to perform the following two logic operations:
- Narrowing down of the design scope
- Pursuing optimal design
The following subsections describe the outlines of these logic operations and the basic methods used for them.
2.1.1ŃĆĆNarrowing down of the design scope
A product development project involves numerous design parameters, such as dimensions or material properties, for each of which an allowable range is specified. Design is an act of extracting a set of design values meeting the design requirements from all possible combinations of design parameters, each having an allowable range (hereafter, such combinations is called the ŌĆ£design spaceŌĆØ). To proceed efficiently with design verification using the design space containing an infinite number of combinations, the computer must first extract the range that may meet the design requirements (design range). Narrowing down of the design scope is the logic operation required here, and the method usually used is the design-of-experiments method. The computer statistically divides the design space into evenly sized segments and performs sampling of the characteristics for the design requirements to grasp the overall nature of the design space.
- <Examples of design-of-experiments methods2) >
-
- Uniform random number method, Monte Carlo method, and Latin hypercube sampling method among others
2.1.2ŃĆĆPursuing optimal design
Narrowing down of the optimal-solution-candidates list is a logic operation for pursuing an optimal solution from an extracted design range (hereafter ŌĆ£optimization algorithmŌĆØ). Among the main methods available are mathematical programming methods and heuristic methods1) .
The former methods derive solutions mathematically. While able to derive rigorous solutions, these methods are subject to constraints requiring that design content to be applied should be, for example, ŌĆ£formulableŌĆØ or ŌĆ£a continuous problem.ŌĆØ
Meanwhile, the latter methods analyze sampled data to find a direction toward better solutions and pursue optimal solutions. Affected by factors such as temporal constraints, these methods derive solutions less rigorous than those derivable by mathematical programming methods. With fewer constraints on design contents, however, these methods are more versatile. For the present trial, we adopted one of the latter as the optimization algorithm, assuming its application to product development involving diverse technical elements.
- <Examples of optimization algorithms2) >
-
- Mathematical programming methods (such as linear programming method or non-linear programming method)
- Heuristic methods (such as genetic algorithm or simulated annealing)
2.2ŃĆĆCAE verification process
The CAE verification process box in Fig. 1 shows the outline process of CAE-based design verification. A process of this kind was conventionally performed with the involvement of designers (e.g., manual work and judgments) and had limitations in verifying many design candidates within a limited period because of its dependence on the human speed of work or thought. Therefore, to be repetitively executed at high throughput, this kind of process must be automatically executable by a computer, giving rise to the need to prepare a program (hereafter ŌĆ£calculation programŌĆØ) for this purpose. More specifically, to externally access and manipulate the functions and data for the linked tools, an API (short for ŌĆ£Application Programming InterfaceŌĆØ) or any other interface defined for each tool must be used to write programs. This interface, however, differs depending on the linked tool. Besides, it takes advanced knowledge and skills to make active use of this interface. Thus, it is by no means easy to prepare programs. The design optimization tools in recent years came equipped standard with interfaces to major commercially available CAD/CAE tools, which made it easier than before to write calculation programs3) .
3. Trial
This chapter presents a case of design optimization in relay development as a specific example of implementation.
3.1ŃĆĆApplication example
A relay is a component that controls the ON/OFF action of an electric circuit in response to electric signal inputs from outside. Fig. 2 shows the main configuration and operating principle of a typical relay.
With the coil OFF and no force on the spring, the contacts are separate from each other (contact OFF state (Fig. 2a)). Then, with the coil ON and the electromagnet energized, the resulting electromagnetic force rotationally displaces the moving piece. The moving piece then pushes the movable spring until the two contacts come into contact with each other (contact ON state (Fig. 2b)). After that, when the coil is turned OFF, the spring╩╝s reaction force detaches the contacts from each other back to the contact OFF state. When the electromagnetic force and the spring reaction force lose balance each other, smooth switching ceases to occur between the contact ON state and the contact OFF state. In extreme cases with the spring reaction force excessively stronger than the electromagnetic force, the moving contact is not displaced, and no transition occurs to the contact ON. As a result, the relay fails to serve its function. It thus follows that the optimization of the balance between the two forces is one of the critical design requirements.
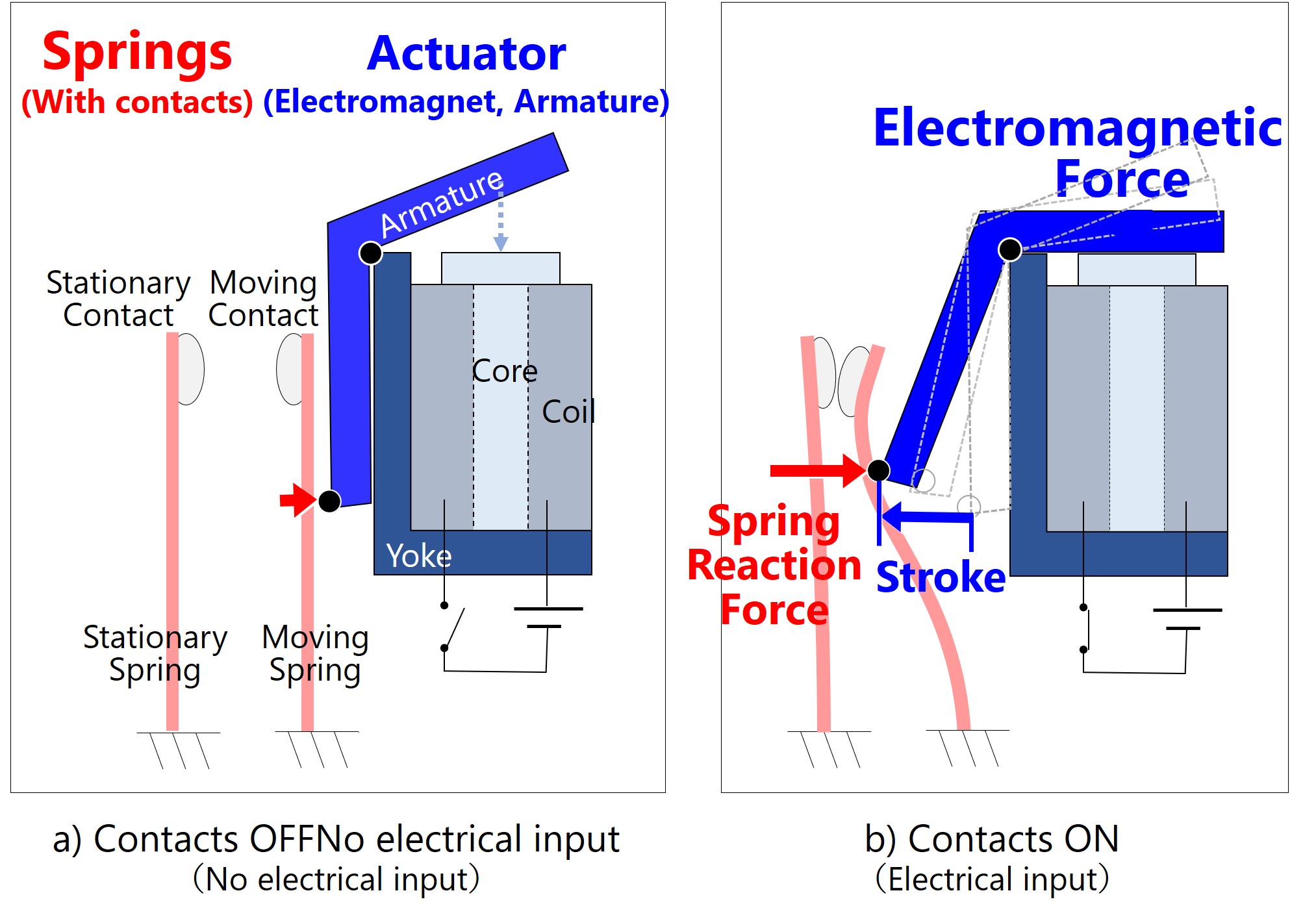
In this trial, with the electromagnetic force characteristics of the actuator as a fixed condition, we worked to derive a spring structure to achieve an optimal balance.
3.2ŃĆĆCalculation program
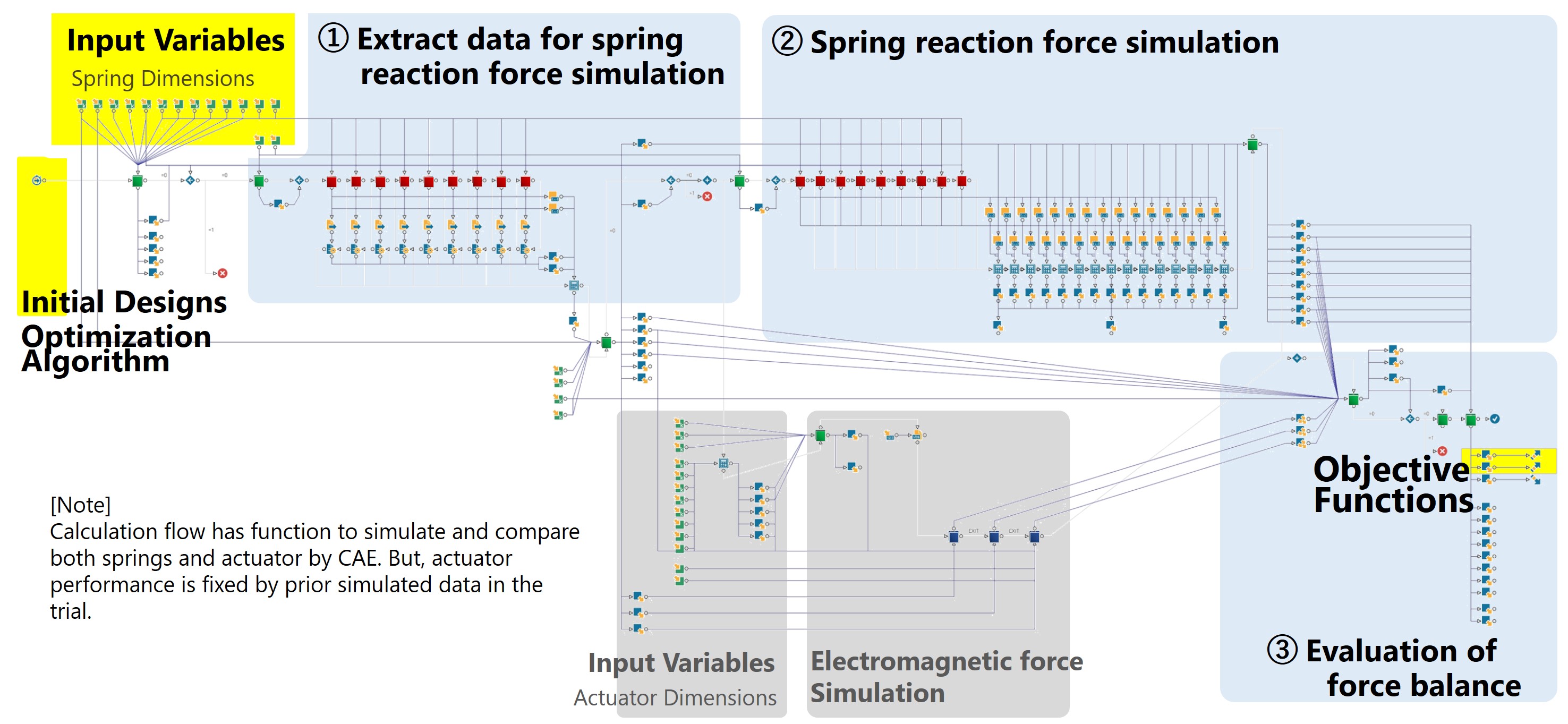
Fig. 3 shows the calculation program prepared for the trial.
3.2.1ŃĆĆDescription of the optimization conditions
First, we specified the following four points as the optimization conditions (the added example shows the content as of the time of the trial).
-
Initial conditions: Design candidates each for use as the starting point of searching for an optimal solution
- To evenly segment the whole design space, we used the uniform random number method as the design-of-experiment method to generate multiple spring design candidates as inputs.
-
Optimization algorithm
- A genetic algorithm (GA)4) was used to ensure versatile support for a design space containing appropriate solutions that were discrete or for design contents for multiple objective functions.
-
Input variables: Parameters constituting design candidates
- Parameters (9 items) were set, including the springs╩╝ thickness-, width-, and length-direction dimensions and the pushed-in position of the movable spring of the actuator. Additionally, a minimum and a maximum value were set as the allowable design range for each parameter.
-
Objective functions: Index/criterion for evaluating the quality of each design candidate
- The indices adopted were the force relationships between the electromagnetic force and the spring reaction force (two items) necessary for smooth switching between the ON/OFF states.
3.2.2ŃĆĆDescription of the CAE verification process
For the theme of the trial presented herein, this process was described in units of tasks or design parameters. To do so, the spring reaction force analysis stage (Section (2) in the figure) hooked up with a commercially available structural analysis CAE tool was placed in the middle between the analysis condition extraction stage (Section (1) in the figure) and the stage for evaluating the force relationship of interest based on analysis results (Section (3) in the figure). The icon-based interfaces provided standard in the design optimization tools were used to describe this process. Moreover, dedicated scripts, macros, and other executables were prepared and implemented for tasks and judgments conventionally performed manually.
3.3ŃĆĆCalculation results
3.3.1ŃĆĆResults achieved by the calculation process
This section refers by the term ŌĆ£calculationŌĆØ to the process that collects appropriate solutions through the repetition of the design candidate extraction and the CAE verification processes shown in Fig. 1. In the present trial, we set the calculation period to two weeks, assuming the conceptual design stage for an actual development theme.
Table 1 shows the results achieved by the calculations performed during the above period. As a result of processing approximately 1,800 design candidates during this period, 728 appropriate solutions were extracted. Formerly, this process involved even tasks, such as CAD model changes, besides manual calculations for design candidate extraction. With all tasks running, the process only managed to complete several calculations per day. After becoming fully computerized and automated, the process was able to perform calculations approximately 180 times more efficiently than before.
| Calculation period | 2 weeks |
|---|---|
| Number of design candidates verified during the calculation period | 1,800 |
| Number of appropriate solutions extracted (design candidates that met design requirements) | 728 |
3.3.2ŃĆĆAnalysis of appropriate solutions
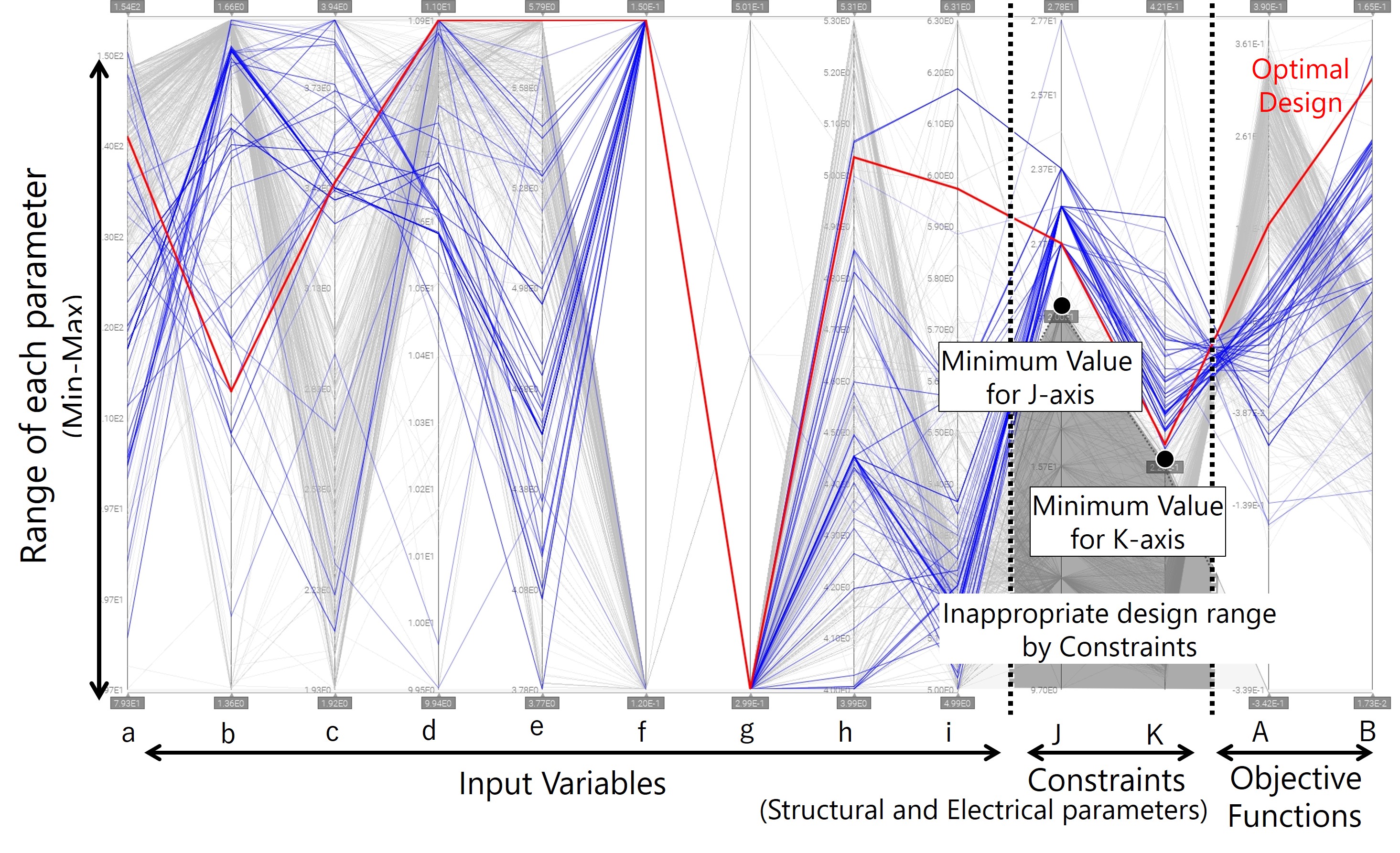
For the process for extracting an optimal solution from the calculation results (appropriate-solutions list), we turned to the designer to determine the validity of the determination indices and criteria. In Fig. 4, the list of appropriate solution data sets obtained from the calculation results is visualized in the form of a so-called multidimensional analysis chart. In the figure, the appropriate solution data (nine input variable values and two objective function values as their verification results) are represented by polygonal lines (blue lines) connecting points above each parameter axis placed in the lateral direction. The vertical axis range in the figure represents the minimum to maximum value range for each parameter.
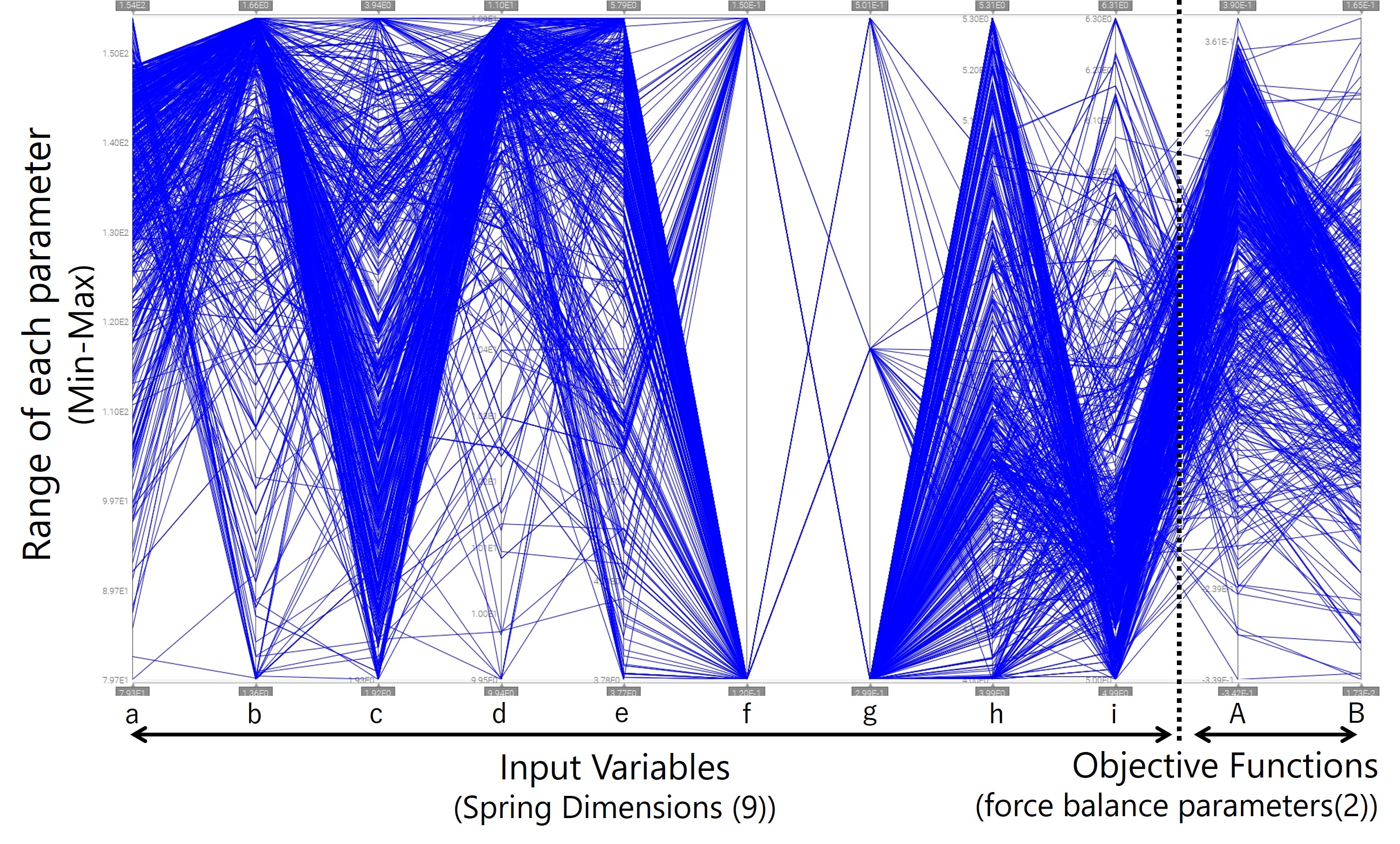
These results show that the input variables fall into the following two groups:
-
Input variables with high design flexibility (a to e, h, and i in the figure)
- Points passed through by polygonal lines are spread all over the range of each axis.
-
Input variables as constraining conditions (e.g., f and g)
- Parameters for which points passed through by polygonal lines concentrate to a substantially limited number of values
3.3.3ŃĆĆOptimal solution search history
Then, Fig. 5 shows a graphical plot of an appropriate-solutions list with Objective Functions A and B set to the x-axis and the y-axis, respectively, for the extraction of an optimal solution from all appropriate solutions. In this figure, the points representing appropriate solutions are color-coded from blue to red in chronological order of verifications.
The present trial was aimed at maximizing Objective Functions A and B (larger-is-better response). Hence, this graph shows points increasingly closer to the ideal in proportion to the proximity to its upper right corner. The increasing number of red points toward the upper right corner of the graph indicates that the optimization algorithm effectively worked and reliably ran design candidate searches toward maximization of the two objective functions.
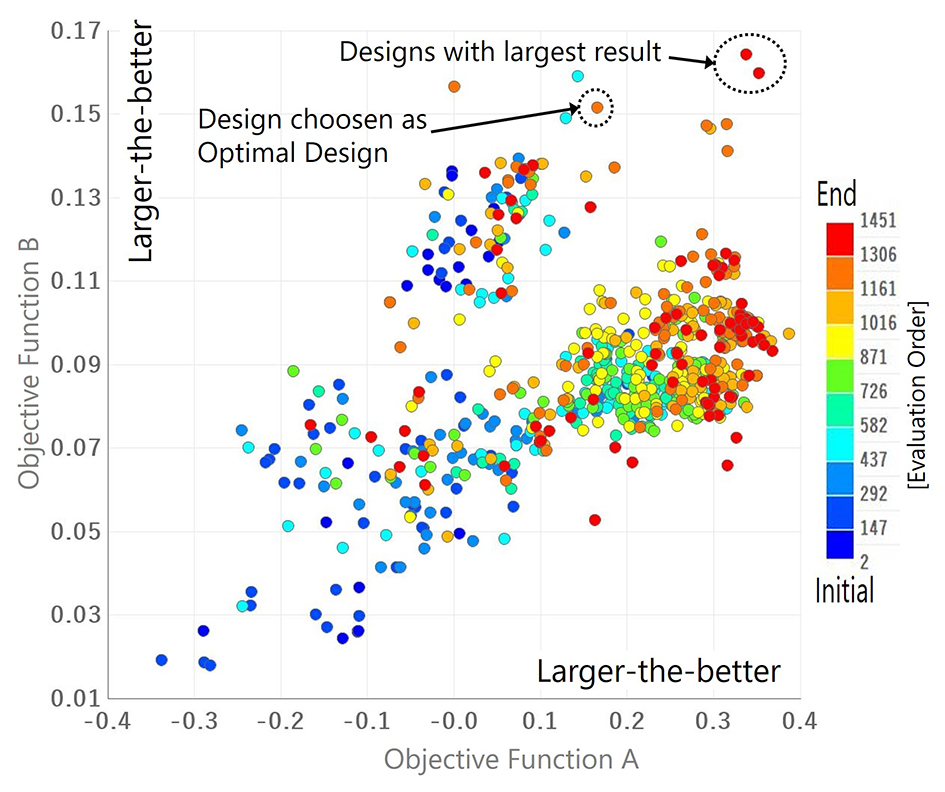
3.4ŃĆĆExtraction of the optimal solution
This section uses Figs. 4 and 5 to explain how the optimal solution was extracted. First, appropriate solutions for maximizing the two objective functions simultaneously, such as the solutions represented by the two points shown in the upper right corner of Fig. 5, were selected as optimal solution candidates and examined for validity. Specific points of view included the behaviors of CAD screen visualizations of input variable values, such as the shapes of the springs or the displacement characteristics of the movable spring. As a result, two structural and electrical characteristics (hereafter ŌĆ£constraining conditions) were identified as insufficiently covered by the design requirements. These constraining conditions are phenomena of the kind on which designers conventionally made empirical judgments and are examples of the successful manifestation of experts╩╝ tacit knowledge as new design requirements.
Fig. 6 shows an improved version of the multidimensional analysis chart in Fig. 4 with the axes for the two manifested constraining conditions added to allow comparative evaluation of the appropriate solutions. Filtering was performed with a new judgment criterion set on each constraining condition axis (the lower limit values set this time on the two axes as the designer╩╝s judgment criteria). As a result, many supposedly appropriate solutions, including the optimal solution candidates represented by the two points in the upper right corners of Fig. 5, turned out to be inappropriate (as shown by the gray polygonal plots). Based on these results, the design candidate (red polygonal line) for maximizing the objective functions was selected as the optimal solution out of the appropriate solutions (blue polygonal lines) that remained after filtering. Note that this optimal solution was verified by physical prototyping and confirmed to provide the expected characteristics.
4. Discussions
This chapter discusses the effectiveness of the design optimization method tried on an actual design problem as well as the challenges to its practical application.
4.1ŃĆĆEffectiveness of our design method
Using the design optimization method presented above, we successfully extracted design candidates of the optimal spring structure to solve the trade-off between the two objective functions. Additionally, we obtained a more feasible solution by not relying on the results worked out by a computer but by visualizing an appropriate-solutions list using a multidimensional analysis chart to add the designer╩╝s perspective.
Moreover, the obtained optimal solution was a shape empirically avoided by designers for fear of negative influences on the other design requirements. As a result of the verification experiment, this optimal solution was confirmed to improve the design requirements, including the ones that had worried designers. This outcome means that our design optimization method is promising as an effective method to logically find an optimal set of values through an exhaustive verification of an entire design space.
4.2ŃĆĆChallenges toward practical application
For future practical application, the method presented above must be able to solve trade-offs among more design requirements. The objective functions and constraining conditions traded off in the trial presented above accounted for only a small portion of the design requirements for the product as a whole. For instance, an increased number of objective functions lead to an increase in the statistically required number of samplings, resulting in an increase in the time required to repeat the CAE verification. The following points must be considered to perform satisfactory design verification within a feasible computing time toward the practical application of our design optimization method:
-
CAE verification time reduction
ŌĆÆ Simplification/rationalization of CAD/CAE models
ŌĆÆ Computational infrastructure enhancement and similar measures -
Optimization of design requirements and design parameters
ŌĆÆ Reduction of the number of design parameters based on the degree of contribution to the technical elements under verification
ŌĆÆ Prioritization of design requirements in accordance with the extent and frequency of rework
4.3ŃĆĆChallenges toward design knowledge accumulation
The main achievement of our design optimization method is the successful conversion of frontline experience-based design techniques and know-how into explicit knowledge in the form of a calculation program. Now the processes and criteria for tasks and judgments of each designer on the development frontline are available as a collection of explicit descriptions. Hence, we can expect to reduce design quality variations attributable to individual designers. Besides, as has been seen with the cases of the constraining conditions added in Section 3.4 or the new design knowledge identified in Section 4.1 as an alternative to conventional design knowledge, we can expect that active use of our design optimization method will help acquire new knowledge and continuously feed it back into calculation programs to allow continuous improvement of our design capabilities.
However, it took us nearly one year to develop the calculation program presented in Section 3.2. The main causes were as follows:
- Converting intuitive/tacit tasks and judgments based on years of experience of skilled designers into explicit knowledge
- Developing an inter-tool interface for auto-executing the employed CAD/CAE tools from a calculation program
The former has been taken up as an important social challenge and addressed through various efforts in recent years. No established solution has, however, come into view. We consider it a critical challenge to establish a framework and a scheme for efficiently and effectively collecting and processing design knowledge to be implemented into calculation programs through cooperation with skilled designers.
Meanwhile, the latter was the cause of why it took us a considerable amount of time to find a technical solution in the trial presented above. Putting it differently, there were many design contents (such as complicated model shapes or special analysis conditions) not fully supported by the interfaces provided standard in the design optimization tools described in Section 2.2. The interface development, in particular, required specialist knowledge necessary for advanced use of design optimization, CAD/CAE, and other tools (e.g., API) and faced the problem of technical cooperation with individual tool vendors.
From the above two challenges and for practical application of design optimization, we consider it essential to develop a framework or network for close cooperation among related parties (designers on the development frontline, design optimization personnel (in charge of development/operation of calculation programs), and individual tool vendors).
5. Conclusions
This paper considered making active use of a design optimization method as one of the design methods for solving trade-offs between multiple technical elements in the upstream part of product development. As the theme of the trial presented herein, we worked on a balanced design between the electromagnetic force of the actuator and the spring reaction force in a relay design, performed the design and verification of many shapes of the springs in a short period, and went beyond the limit of conventional design knowledge and successfully extracted an optimal solution for overcoming the trade-off.
We intend to deploy the design optimization method presented herein to the frontlines of various product developments in our company. For this purpose, we will collect and accumulate examples of design optimization between various technical elements. Then, we will compile designers╩╝ knowledge and interface information available from such examples into template calculation programs for each main design item to efficiently deploy our method and promote design capability enhancement toward further reduction of design rework.
References
- 1)
- Y. Ikeda, ŌĆ£Front-Loading Method for Improving Design Process Capabilities,ŌĆØ (in Japanese), Toshiba Review, vol. 62, no. 9, pp. 2 ŌĆō 8, 2007.
- 2)
- H. Yamakawa et al., Optimal Design Handbook ŌĆö Fundamentals, Strategies, and Applications. Tokyo: Asakura Publishing Co., Ltd., (in Japanese), 2003.
- 3)
- Esteco S.p.A, modeFRONTIER User╩╝s Guide, (in Japanese), 2019.
- 4)
- N. Sannomiya et al., Genetic Algorithms and Optimization. Tokyo: Asakura Publishing Co., Ltd., (in Japanese), 1998, 185p.
The names of products in the text may be trademarks of each company.
















