Model-less Grasping Points Estimation for Bin-Picking of Non-Rigid Objects and Irregular-Shaped Objects
- Bin picking
- Grasping point estimation
- Robotics
- 3D recognition
- Depth map processing
In this paper, we deal with the grasping points estimation for robotic bin picking. Usually, grasping points are estimated by using 3D CAD of the object to be grasped. However, it becomes difficult to estimate the grasping points for non-rigid objects or irregular-shaped objects that do not have any specific 3D CADs. In order to realize bin picking of non-rigid objects and irregular-shaped objects, we employ a model-less grasping point estimation method that can estimate the grasping points without using 3D CAD. As an estimation method for a two-fingered hand, we propose a method that detects the insertion candidates independently for the left and right fingers and pairs the candidates to efficiently estimate the grasping candidates with multiple opening widths of the hand. As an estimation method for a suction hand, we propose a method that extracts flat areas based on the variance of the local surface orientation of a depth map and estimates the optimal grasping points from the flat areas. Using the proposed methods for two-fingered hands and suction hands, a robot successfully grasped non-rigid objects and irregular-shaped objects with a grasping success rate of 96%. Moreover, the computation time of both proposed methods is 250 msec on the Intel Core i7-7700 @ 3.60 GHz, which allows real-time bin picking.
1. Introduction
Many tasks on manufacturing shop floors and in logistics warehouses involve workers picking and moving objects to specified locations. For example, when feeding parts onto the production line in an automotive factory, the line workers pick randomly piled parts one by one from containers. Such a line production system requires a large number of personnel, including workers in charge of only simple tasks, such as parts picking. Meanwhile, with the worsening working population shortage in recent years, demands are rising for machines replacing and automating such simple tasks. As a method for such automation, the so-called part feeders are sometimes used, which are dedicated machines used exclusively for parts feeding. Each part feeder is, however, a custom-built machine designed for a specific type of part. Hence, they pose the problem of an increased number of production line start-up person-hours. For this problem, a general-purpose robot able to pick various randomly piled parts may be installed to automate parts feeding and reduce the number of line start-up person-hours.
For automated bin picking to work, optimal grasp points for the robot must be estimated from images/depth maps capturing the target objects to grasp. Where there is a need to pick rigid bodies, such as industrial parts, 3D CAD models are used to estimate the r 6D pose of the target objects to grasp1,2). When it comes, however, to shape-variable objects (non-rigid objects), such as cables or bags and pouches, or objects individually different in shape (irregularly shaped objects), such as food or agricultural products, no specific 3D CAD models are available, making it difficult to estimate the 6D pose of the target objects to grasp. As a solution to this problem, a model-less grasp point estimation method is effective. This method makes it possible to estimate the grasp points and rotations of a robot hand from its shape and measurement data, instead of estimating the 6D pose of the object, in other words, without the need for a 3D model of the target object to grasp. Where an estimation must be made of the type and posture of a non-rigid object or an irregularly shaped object, a model-less grasp point estimation is performed as a preparatory processing step. Accordingly, high processing speed is required as much as the estimation of stable grasp points.
In this paper, we propose high-speed, model-less grasp point estimation methods for grasping non-rigid objects and irregularly shaped objects. Because industrial robots are usually equipped with a two-fingered hand or a suction hand, we propose a method intended for each of these two types of hands. Fig. 1 shows a typical example of a two-fingered hand and that of a suction hand.

2. Related works
Model-less grasp point estimation methods fall broadly into machine learning-based methods that estimate the optimal grasp points of target objects to grasp by learning and hand model-based methods that use a robot hand model and search for optimal grasp points for the shape of the hand.
2.1ŃĆĆMachine learning-based grasp point estimation
In a model-less grasp point estimation, no information on the object is available beforehand. Hence, many proposals have been made for methods to learn the optimal grasp points of various objects through a deep neural network (DNN)3–10’╝ē. Redmon et al. proposed a method that defines the correspondences between a 7├Ś7 grid of split input images and a 7├Ś7 DNN-output feature map and obtains by regression calculations the six-dimensional data (coordinates for the center of grasping, width and height, rotational angle, and confidence value for grasping) of a two-fingered hand from each pixel of the feature map6’╝ē. There have also been proposals made for methods of estimating a target grasp area by solving a semantic segmentation classification problem using a fully convolutional network (FCN)7,8’╝ē. Dex-Net 3.0/4.0 learns a DNN that computes the robustness of grasping for patch images around grasp points as probability9,10’╝ē. With the use of a DNN as in these methods, a high-accuracy grasp point estimation becomes available but may be challenging to introduce because it requires a high-performance computing machine and a massive amount of training image with annotation.
2.2ŃĆĆHand model-based grasp point estimation
A method of searching for grasp points from images based on the shape of a robot hand is available as a grasp point estimation method that does not require machine learning. In a fast graspability evaluation (FGE)11,12’╝ē, 2D binary images of the hand╩╝s shape are convolved into the object segments in depth maps to perform high-speed grasp point searching. When applied to a two-fingered hand, the FGE faces the problem of increased computing time. More specifically, non-rigid or irregularly shaped objects are individually different in size and hence require searching for grasp points for multiple hand-opening widths. As a result, the required computing time increases proportionally to the number of hand-opening widths. In the application of FGE to a suction hand, the flatness of the object segments to be extracted is not taken into consideration: suction grasping of irregularly surfaced segments results in the problem of a reduced grasp success rate.
In this paper, we propose model-less grasp point estimation methods, which provide the advantage of saving the need for preparing a large amount of training images and opt instead for a hand model-based grasp point estimation as a solution to overcome the problems mentioned above with FGE. Being aware of the difficulty of developing a single algorithm able to define the optimal points for both a two-fingered hand and a suction hand to grasp an object, we propose two separate algorithms for a model-less grasp point estimation for a two-fingered hand and a suction hand.
3. Model-less grasp point estimation for the two-fingered hand
3.1ŃĆĆOutline of the algorithm
Non-rigid or irregularly shaped objects, such as food products, vary in size from one to another. Hence, in the estimation of the optimal grasp points for a two-fingered hand, searching must be performed for multiple hand-opening widths. As a result, the required computing time increases proportionally to the number of hand-opening widths. As a solution to this problem, we propose the detection of insertion point candidates separately for each of the right and left fingers of the two-fingered hand (one-finger insertion point candidate detection) and the pairing of the left-finger and right-finger insertion point candidates to achieve high-speed grasp point candidate estimations for multiple hand-opening widths. Fig. 2 shows the overall view of the algorithm. As an illustrative example, a randomly piled deep-fried chicken nuggets is used here. A depth map based on 3D sensor measurements is used for the grasp point estimation. To search for grasp point candidates in various directions around the optical axis of the 3D sensor, rotated depth maps in increments of 
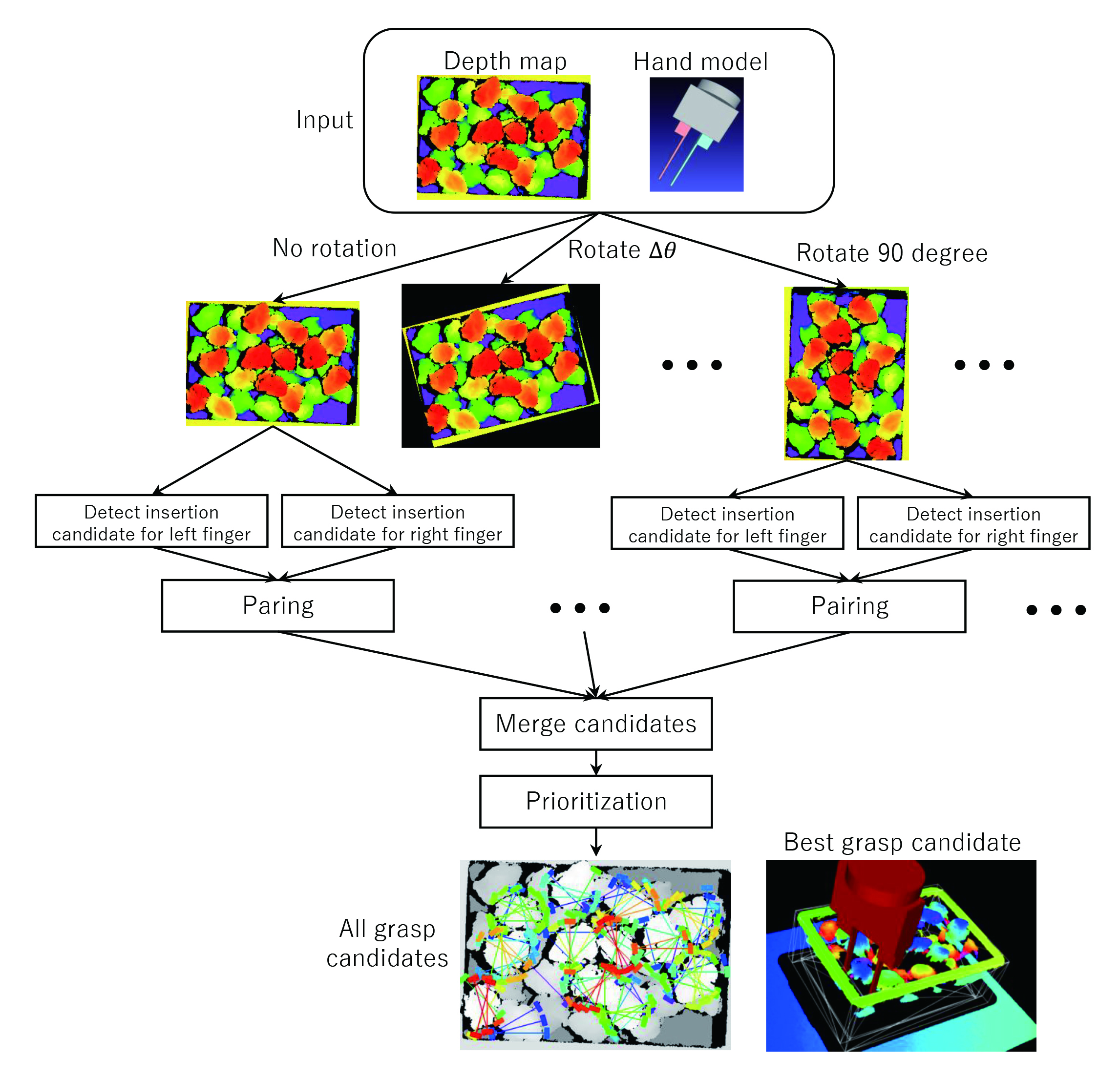
3.2ŃĆĆOne-finger insertion point candidate detection
Insertion point candidates are detected separately for each of the right and left fingers of the two-fingered hand. The following two grasping conditions are essential for the two-fingered hand to grasp an object stably:
- 1. There is an edge of a height sufficient to allow a firm grasp of an object.
- 2. There is a sufficient amount of space to allow finger insertion without causing any interference.
One-finger insertion point candidates meeting these conditions hence need to be detected. First, a horizontal differential filter is applied to the original depth map to detect the distance edge intensity in the horizontal direction. Then, pixels with an absolute distance edge intensity value equaling or exceeding a threshold are extracted. Here, pixels with a minus sign for the distance edge intensity show a change in distance relative to the 3D sensor from far to near along the plus direction of the 


Fig. 3 One-finger insertion point candidates and pairing results
3.3ŃĆĆPairing
The obtained left-finger and right-finger insertion point candidates undergo pairing to generate grasp point candidates. For a given left-finger insertion point candidate, a right-finger insertion point candidate to be paired with it exist in the horizontal direction of same 



3.4ŃĆĆPriority ordering
The grasp point candidates searched from multiple rotated depth maps are merged for rearrangement in order of priority. The graspability of an object can be defined from various perspectives, such as its proximity, the height of its convex portion, and the linearity of its gripping portion. Our proposed technique uses three different types of graspability metrics, in other words, distance, convex portion height, and gripping portion╩╝s linearity in combination to obtain comprehensive evaluation scores. This method performs priority ordering by arranging grasp point candidates in descending order of their evaluation scores.
4. Model-less grasp point estimation for the suction hand
4.1ŃĆĆOutline of the algorithm
The following two grasping conditions are of importance for the suction hand to grasp an object stably:
- 1. The suction hand vertically approaches the surface of the actual grasp target object to achieve a firm suction.
- 2. The suction hand suctions on a flat area on the grasp target object so as not to let air leak from its suction pad.
For the satisfaction of these two suction-grasping conditions, flat area extraction is performed based on variance of the normal vectors in the depth map to estimate grasp point candidates. A normal vector represents the local planar orientation of 3D measurement data. Therefore, an area can be said to be a flat area when the normal vectors around it are oriented in the same direction, in other words, when variance of the normal vectors is small . Because the normal vectors obtained at the time of flat area extraction are reusable, the approach angle for the grasp point can be determined without the need for a complicated computing process, allowing high-speed grasp point estimations.
The flow of the suction-grasp point estimation by our proposed technique goes as follows: first, a flat area on the object is extracted from the depth map to determine the graspability (grasp evaluation score) based on each pixel in the flat area. Then, based on the grasping pose at a point with a high grasp evaluation score, the 3D points in the surrounding area is examined for interference with the hand model to find and register interference-free points as grasp point candidates. The rest of this paper uses, as an example, the depth map of randomly piled hinges in Fig. 4(a) to explain in detail our proposed technique.
4.2ŃĆĆFlat area extraction based on variance of normal vectors
A planar model that satisfies 





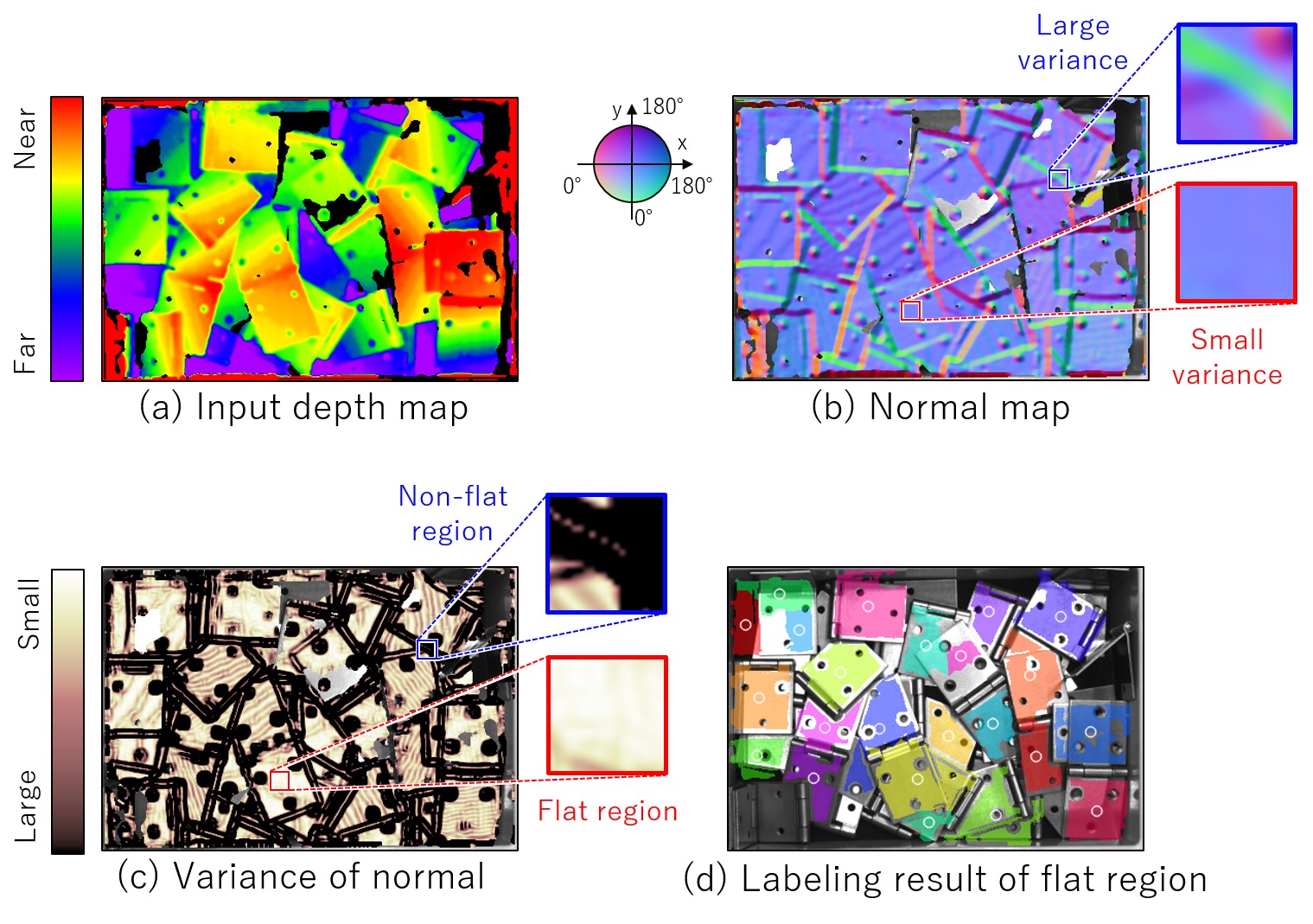
A flat area shows a lower variability of normal vectors, whereas an irregularly surfaced area shows a higher variability of normal vectors. Hence, for each local rectangular area, the variance of normal vectors must be calculated (Fig. 4(c)). Then, if the variance of normal vectors thus determined is below a given threshold, a binary image of each flat area is generated by plane label assignment. The binary image of each flat area undergoes a labeling process to produce a labeled flat area (Fig. 4(d)).
The above process allows the extraction of the flat areas in randomly piled objects. If, however, a multiple number of target objects to grasp of the same height are adjacent to one another, the differences between the distances near the object boundaries will be minute, posing the problem of under-segmentation, in other words, extraction of a multiple number of object planes as a single object plane. Then, an area segmentation process based on the Watershed algorithm13’╝ē is applied to the labeled flat area image. The Watershed algorithm consists of flat area image distance transformation, area erosion , relabeling, and relabeled area dilation . Distance transformation is a process that computes the distance of each pixel in a flat area based on non-flat area data. In the resulting image, a planar pixel at a considerable distance from non-flat areas has a large value, while one at a close distance from non-flat areas has a small value. Therefore, when pixels with a small distance transformation value are extracted from flat areas, the flat areas undergo erosion processing , resulting in the division of the flat areas of multiple objects into segments. Then, the flat areas segmented by the erosion processing are relabeled. The relabeled flat areas are allowed to dilate until they reach their pre-erosion sizes or come into contact with each other. This series of processes reduces under-segmentation and hence allows accurate flat area extraction.
4.3ŃĆĆGrasp point candidate detection based on grasp evaluation score
Where there is a need to identify a point convenient for grasping within each extracted flat area, a grasp evaluation score calculation is performed. A grasp evaluation score represents the graspability within a flat area, and this score is determined comprehensively based on several types of graspability metrics, such as the distance to the planar center of gravity, the normal vector dispersion, and the grasp approach angle. In practice, thresholds are set for these types of graspability metrics to divide their respective scale of graspability into three score levels {A, B, and C}. An ultimate grasp evaluation score is assigned to be higher proportionally to the number of A╩╝s and lower proportionally to the number of C╩╝ s. This process is performed for all the pixels in the flat area. Fig. 5(a) shows the results of the grasp evaluation score calculation. The variance of normal vectors was calculated at the time of flat area extraction, and the grasp approach angle need not be calculated by a separate process because the normal direction is used as such. Thus, the grasp evaluation score for each flat area can be calculated at high speed.
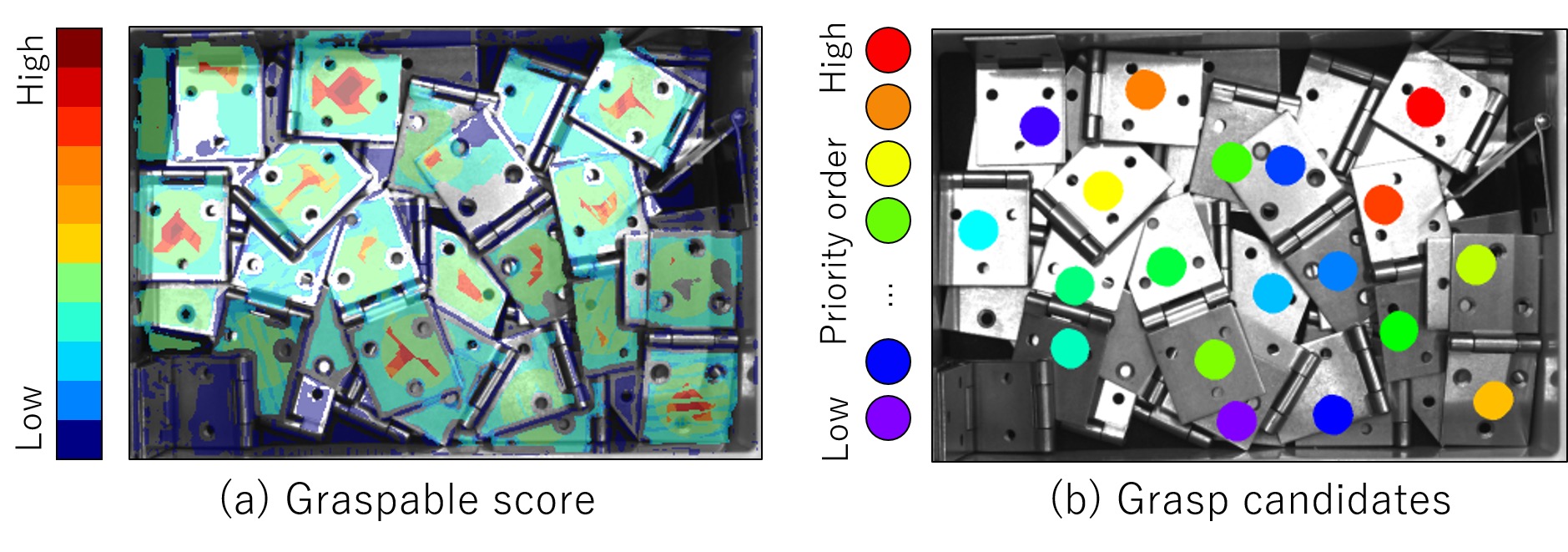
After grasp evaluation scores are calculated for all pixels in the flat areas, grasping poses are calculated from the image coordinates in descending order of their grasp evaluation scores. Then, the hand model in each calculated grasping pose is examined for interference with the 3D points in the surrounding area. The approach angle for calculating each grasping pose can be determined while saving the need for unnecessary calculations by the reuse of the normal vectors estimated at the time of flat area extraction. For each coordinate position, grasping-pose calculation and interference determination are repeated. Then, a coordinate position determined as interference-free is registered as a grasp point candidate. This process is performed for all the flat areas. Fig. 5(b) shows the grasp point candidate registered for each flat area.
4.4ŃĆĆPriority ordering
After grasp point candidates calculation, each grasp point candidate is given a priority order. Basically, a grasp point with a high grasp evaluation score is given a high priority. In some cases, however, a multiple number of grasp point candidates occur with an evaluation score equivalent to that of the others. In such cases, from a set of graspability metrics, such as the distance to the planar center of gravity, the variance of normal vectors, and the grasp approach angle, a desired metric is selected to sort grasp point candidates of the same evaluation score.
5. Evaluation experiment
5.1ŃĆĆEvaluation method
We performed an evaluation experiment to confirm the effectiveness of our proposed techniques. We used a 3D sensor to capture images of randomly piled target objects to grasp. From the captured images, grasp points were estimated. We used a six-axis vertical articulated robot to pick up each grasp target object based on the estimated grasp point and place them to their respective specified locations. The robot makes a grasp try for each high-priority grasp point within its movable area . For each type of object, the grasp success rate was calculated based on the ratio between the number of grasp tries made by the robot and the number of objects picked and successfully placed to the specified location. Moreover, we also evaluated the processing time required for grasp point estimation per image. Because the grasp point estimation process is performed every time before the robot makes a try, we calculated the average required processing time per run of the grasp point estimation process. The 3D measurement sensor and the vertical articulated robot used this time were an iDS-manufactured Ensenso X36 and an OMRON-manufactured Viper650, respectively. A computer equipped with an Intel (R) Core (TM) i7-7700 @ 3.60 GHz CPU was used to measure the processing time.
5.2ŃĆĆEvaluation results for the two-fingered hand
The grasp target objects used in the evaluation experiment on our model-less grasp point estimation method for the two-fingered hand were the four different types of objects differing in, for example, size, shape, and material, as shown in Fig. 6. Among these types of objects, deep-fried chicken nuggets, potatoes, and bananas are irregularly shaped objects, while power supply cables are non-rigid objects.

Table 1 shows the grasp success rate and the required processing time for each type of grasp target objects.
| Grasp target object | No. of successful placements achieved/ no. of tries made |
Grasp success rate [%] |
Processing time [msec] |
|---|---|---|---|
| Deep-fried chicken nugget | 93/93 | 100.0 | 211 |
| Potato | 159/160 | 99.4 | 285 |
| Banana | 110/124 | 88.7 | 197 |
| Power supply cable | 39/40 | 97.5 | 221 |
| Average | 96.4 | 229 |
The results in Table 1 show that a high average grasp success rate of 96.4% was achieved. The contributory factor to this achievement was the estimated optimal hand-opening widths that allowed the maximization of the number of grasp point candidates relative to that achievable by a fixed hand-opening width. Globular objects, such as deep-fried chicken nuggets or potatoes, showed particularly high grasp success rates because they stably allowed detection of grasp point candidates from various angles. Only bananas showed a low grasp success rate of 88.7% because they were more often grasped unstably by a tricky handhold, such as either of the two ends. The average required processing time per run of the grasp point estimation process was approximately 229 msec, fast enough for a robot hand system to perform high-speed bin picking in real time. This achievement was possible because the pairing process after one-finger insertion point candidate detection saved the need for grasp point searching for multiple hand-opening widths and helped to reduce the amount of computations significantly. Fig. 7 shows typical results of grasp point estimation for the two-fingered hand.

5.3ŃĆĆEvaluation results for the suction hand
The grasp target objects used in the evaluation experiment on our model-less grasp point estimation method for the suction hand were the five different types of non-rigid objects differing in, for example, size, shape, and material as shown in Fig. 8.

Table 2 shows the grasp success rate and the required processing time for each grasp target object.
| Grasp target object | No. of successful placements achieved/ no. of tries made |
Grasp success rate [%] |
Processing time [msec] |
|---|---|---|---|
| Flat cable | 38/39 | 97.4 | 72 |
| Hand soap bottle | 18/18 | 100.0 | 112 |
| Mayonnaise packet | 114/120 | 95.0 | 91 |
| Plastic part | 65/68 | 95.5 | 75 |
| Hinge | 73/75 | 97.3 | 67 |
| Average | 97.0 | 83 |
The results in Table 2 show that a grasp success rate of 95% or more was achieved for all the grasp target objects. Thanks to a flatness-based plane extraction process and the determination of a proper grasp approach angle, stable suction grasping became possible. Hand soap bottles, in particular, showed a high grasp success rate because of their large physical size and relatively large flat area. The main cause of failed grasp attempts was that a grasp approach toward the vicinity of object boundaries occurred when object boundary determination on the depth map was difficult because of the small thickness of the objects, such as mayonnaise packets. Besides, some attempts to grasp plastic parts with shallow grooves on their surface failed due to the air leakage during suction.
The average required processing time per run of the grasp point estimation process was approximately 83 msec, fast enough for a robot hand system to perform high-speed bin picking in real time. The hand soap bottles required a longer processing time per grasp point candidate search or grasping-pose calculation because of the large size of the flat areas extracted from their image. Fig. 9 shows typical results of grasp point estimations for the suction hand.

6. Conclusions
In this paper we proposed model-less grasp point estimation methods for a two-fingered hand and a suction hand. The grasp point estimation method for the two-fingered hand detects insertion point candidates separately for each of the right and left fingers of the two-fingered hand and makes the combinations of right-and left-finger insertion point candidates to perform high-speed searches for grasp point candidates for multiple hand-opening widths. The grasp point estimation method for the suction hand extracts flat areas based on the variance of normal vectors in a depth map and estimates grasp point candidates to achieve stable suction grasping of objects. When put to the tests of picking randomly piled non-rigid objects and irregularly shaped objects by the two methods proposed herein for the two-fingered hand and the suction hand, our robot achieved average grasp success rates of 96.4% and 97.0% and also achieved high processing speeds of 229 msec and 83 msec on an Intel (R) Core (TM) i7-7700 @ 3.60 GHz CPU.
Future works is further improvement of the grasp success rate. Solutions must be developed with a focus on the causes of failed grasp attempts. Another challenge is usability improvement through the development of an automatic parameter tuning function able to replace the manual paramete tuning currently used for various parameters involved in our proposed techniques.
References
- 1)
- Y. Konishi, Y. Hanzawa, M. Kawade, and M. Hashimoto, ŌĆ£Fast 6D Pose Estimation from a Monocular Image Using Hierarchical Pose Trees,ŌĆØ in Proc. Eur. Conf. Comput. Vision, 2016, pp. 398-413.
- 2)
- Y. Konishi, K. Hattori, and M. Hashimoto, ŌĆ£Real-Time 6D Object Pose Estimation on CPU,ŌĆØ in Proc. Int. Conf. Intelligent Robot. and Syst., 2019, pp. 3451-3458.
- 3)
- I. Lenz, H. Lee, and A. Saxena, ŌĆ£Deep Learning for Detecting Robotic Grasps,ŌĆØ Int. J. Robot. Res., vol. 34, no. 4-5, pp. 705 ŌĆō 724, 2015.
- 4)
- J. Mahler, J. Liang, S. Niyaz, M. Laskey, R. Doan, X. Liu, et al., ŌĆ£Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics,ŌĆØ in Proc Robotics: Science and Syst., 2017.
- 5)
- S. Caldera, A. Rassau, and D. Chai, ŌĆ£Review of Deep Learning Methods in Robotic Grasp Detection,ŌĆØ Multimodal Technologies and Interaction, vol. 2, no. 3, pp. 57ŌĆō 80, 2018.
- 6)
- H. Liang, X. Ma, S. Li, M. Grner, S. Tang, B. Fang, et al., ŌĆ£PointNetGPD: Detecting Grasp Configurations from Point Sets,ŌĆØ in Proc. Int. Conf. Robot. Automation, 2019, pp. 3629-3635.
- 7)
- J. Redmon and A. Angelova, ŌĆ£Real-Time Grasp Detection using Convolutional Neural Networks,ŌĆØ in Proc. Int. Conf. Robot. Automation, 2015, pp. 1316-1322.
- 8)
- H. Kusano, A. Kume, E. Matsumoto, and J. Tan, ŌĆ£FCN-Based 6D Robotic Grasping for Arbitrary Placed Objects,ŌĆØ in Proc. Int. Conf. Robot. Automation: Warehouse Picking Automation Workshop, 2017.
- 9)
- J. Mahler, M. Matl, X. Liu, A. Li, D. Gealy, and K. Goldberg, ŌĆ£Dex-Net 3.0: Computing Robust Vacuum Suction Grasp Targets in Point Clouds Using a New Analytic Model and Deep Learning,ŌĆØ in Proc. Int. Conf. Robot. Automation, 2018, pp. 1-8.
- 10)
- J. Mahler, M. Matl, V. Satish, M. Danielczuk, B. DeRose, S. McKinley, et al., ŌĆ£Learning Ambidextrous Robot Grasping Policies,ŌĆØ Sci. Robot., vol. 4, no. 26, eaau4984, 2019.
- 11)
- Y. Domae, H. Okuda, Y. Taguchi, K. Sumi, and T. Hirai, ŌĆ£Fast Graspability Evaluation on Single Depth Maps for Bin Picking with General Grippers,ŌĆØ in Proc. Int. Conf. Robot. Automation, 2014, pp. 1997-2004.
- 12)
- K. Mano, T. Hasegawa, Y. Takayoshi, H. Fujiyoshi, and Y. Domae, ŌĆ£Fast and Precise Detection of Object Grasping Positions with Eigenvalue Templates,ŌĆØ in Proc. Int. Conf. Robot. Automation, 2019, pp. 4403-4409.
- 13)
- L. Vincent and P. Soille, ŌĆ£Watersheds in digital Spaces: An efficient algorithm based on immersion simulation patterns,ŌĆØ IEEE Trans. Pattern. Anal. Mach. Intell., vol. 13, issue 6, pp. 583-598, 1991.
The names of products in the text may be trademarks of each company.
















