A Compensator that Negate the Influence of Grid Impedance based on Frequency Sweep Estimation Technique
- Power conditioning system
- Miniaturization of AC reactor
- Grid impedance estimation method
- Impedance suppression compensator
In order to reduce the volume and cost of the PCS (Power Conditioning System), miniaturization of AC reactors (ACL) of inverters has been studied. If the ACL impedance value becomes smaller than the Grid-impedance between PCS and Grid, it is pointed out that a controllability of PCS has a risk of unstable. However, trying to improve the stability of control design, there will be a concern that the CPU calculation amount will increase. In this paper, we propose a control method that PCS itself estimates Grid-impedance with a small amount of calculation amount and set optimal control parameters as well. This control system is able to secure the stability according to the Grid-impedance after PCS installation, and further achieve a miniaturization of the ACL. As a result, it can contribute to downsizing and low cost of the entire PCS.
1. Introduction
1.1 The significance of spreading the use of renewable energy
In modern society, which relies on electronics, electricity is an essential source of energy. However, according to a survey conducted by the International Energy Agency (IEA), electricity generated from coal, natural gas and petroleum accounted for 81.4% of global power generation in 2015, meaning the global power generation is dependent on exhaustible resources 1). If this power generation continues, there is concern that global power generation that can meet the demand of society cannot be sustained. To solve this issue, the use of renewable energy has been taken into consideration. Although the high introduction cost of renewable energy had conventionally prevented its widespread use, introduction costs have been reduced as a result of improvement in efficiency and the downsizing of electric power converters. To realize a sustainable society, it is necessary promote the use of renewable energy through further cost reduction hereafter.
1.2 The role and issue with PCS
We are offering a PCS (Power Conditioning System) focusing on photovoltaic power generation as renewable energy. A PCS is a system that converts electricity generated by photovoltaic cells into AC power used in a grid power network for interconnection. Fig. 1 shows the external appearance of the PCS for photovoltaic power generation.

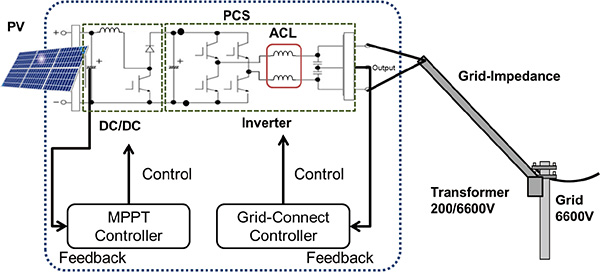
Fig. 2 shows the schematic view of a PCS with photovoltaic cells connected. The PCS consists of the following two electric converters: a DC/DC converter in the preceding stage and an inverter in the subsequent stage. The converter in the preceding stage controls the input power from the photovoltaic cells to constantly maximize it through the Maximum Power Point Tracking Control and feeds it to the inverter in the subsequent stage. The inverter in the subsequent stage converts DC power into AC power and feeds the power to the grid network while tracking grid variations through the Grid-Connect Control.
Among the parts which construct these electric converters, the reactor makes up a significant proportion of the cost and volume. In particular, downsizing the AC reactor (hereinafter referred to as ŌĆ£ACLŌĆØ) that is used for the LC filter of the inverter leads to downsizing and cost reduction of the entire PCS.
However, when ACL is downsized, it has to face a problem that Grid-Connect Control becomes unstable due to current resonance of reactance components (





1.3 The position of previous studies and this paper
The suppression of resonance using a control software is being considered as the method of downsizing the ACL.
Among previous studies, there are documents 2) ŌĆō 4) reported cases where robust control such as H Ōł× control and LQG (Linear-Quadratic-Gaussian) controllers are used as the methods of ensuring stability without estimating the grid impedance. However, since the computing load of the CPU becomes very high in such cases, these methods are not practical for PCS.
Methods of designing a controller based on the estimated grid impedance have also been suggested. The literature 5) suggested the injection of harmonics into the output voltage to estimate the absolute impedance value based on the amplitude variation. However, this method requires the mounting of several SOGIs (Second Order Generalized Integrators) with a high computing load to enhance the accuracy. The literature 6) suggested the method of estimating the impedance from the output voltage regulation when active and inactive powers were varied. However, this method requires the building of a control system for operating active and reactive powers independently, and there is concern that the computing load may increase.
This paper describes a method which negates the influence of grid impedance so that even a small ACL becomes stable. Since the compensator optimizes the compensator parameter based on the grid impedance value estimated according to a computing method simpler than the one used in previous studies, there is no need to design ACLs based on the maximum

Chapter 2 describes the influence and issues with grid impedance made when a conventional control system is built. Chapter 3 shows how to estimate grid impedance and design the compensator. Chapter 4 presents the effectiveness of the suggested method based on the simulation results, and Chapter 5 gives a summary of this paper.
2. The influence of grid impedance on Grid-Connect Control
2.1 The configuration of Grid-Connect Control
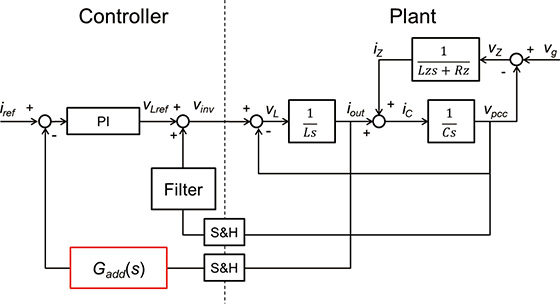
Fig. 3 shows the complete view of the Grid-Connect Control of the inverter. The Grid-Connect Control is made up of a command value generation section which generates a current command value synchronized with the AC voltage phase of the Point of Common Coupling (PCC), a current controller which controls output current, and a controlled object consisting of the inverter circuit, grid impedance and grid voltage. The control system manipulates the inverter modulation factor based on the duty width of the PWM signal to control output current.
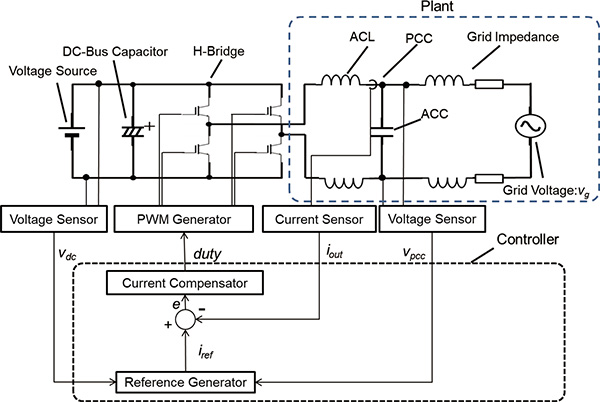
2.2 Unstable current control caused by grid impedance
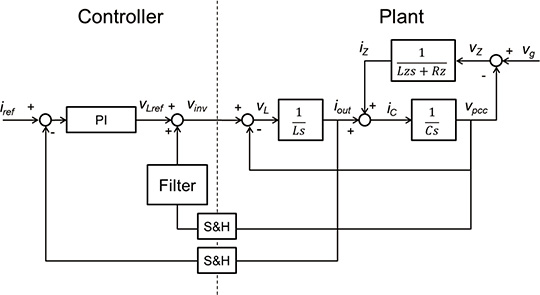
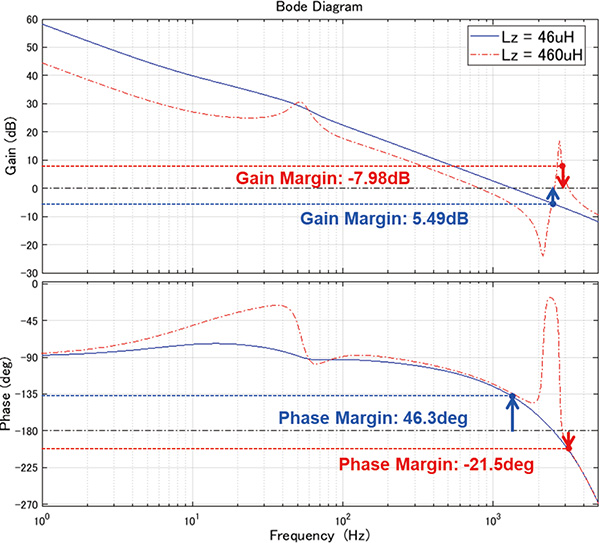
To determine the stability of the current control system on Matlab/Simulink, we modeled the control system and controlled object. Fig. 4 shows the block diagram of the modeled current control system. Fig. 5 shows the Bode diagram of the open loop transfer functions of the current control system. The parameters of respective conditions are as shown in Table 1.
The graphs indicated with solid lines in Fig. 5 show the open loop transfer functions when



The graphs indicated with dashed lines in Fig. 5 show the open loop transfer function when



| Condition No. | 1 | 2 |
|---|---|---|
| Grid voltage | 202 Vrms | 202 Vrms |
| Grid voltage frequency | 60 Hz | 60 Hz |
Imaginary part of grid impedance:  |
46 ╬╝H | 460 ╬╝H |
Real part of grid impedance:  |
38 m╬® | 380 m╬® |
| AC reactor | 720 ╬╝H | 720 ╬╝H |
| AC capacitor | 12 ╬╝H | 12 ╬╝H |
| PWM carrier frequency | 10 kHz | 10 kHz |
| P gain of PI controller | 6.48 | 6.48 |
| I gain of PI controller | 454.4 | 454.4 |
3. Design of the control compensator
3.1 How to estimate grid impedance
Fig. 6 shows the equivalent circuit of the controlled object. In this figure and the equation to be described below, the inductance value of the ACL and the capacitance value of the ACC are expressed as




The grid connection point voltage

-
(1)
In the equation (1),

-
(2)
Where,



-
(3)
Fig. 7 shows the equation (3) graphically.
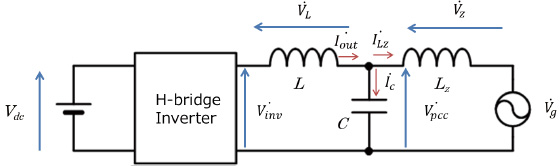
Among the variables shown in the equation (3),







In addition, although the output filter of the inverter shows an example of LC filter this time,





3.2 The configuration and algorithm of the suggested system
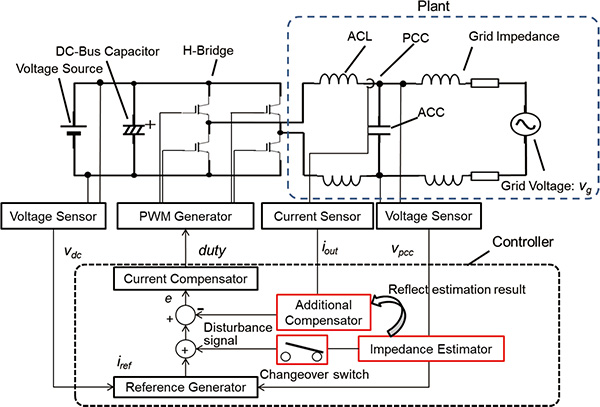
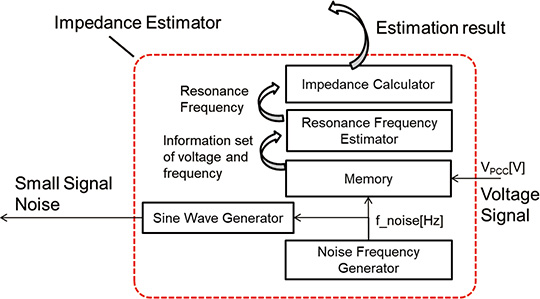
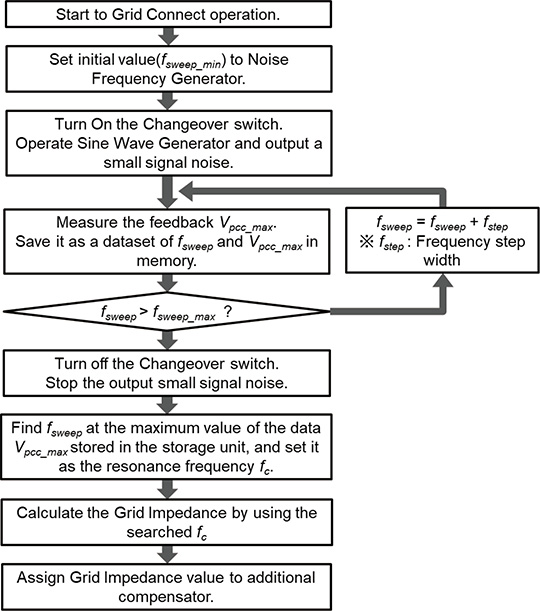
Fig. 8 shows the configuration of the entire system suggested, which was created by adding the impedance estimation section, the impedance suppression compensator section and the configuration changeover switch to the configuration shown in Fig. 3. Fig. 9 shows the internal configuration of the added impedance estimation section.
The procedure for estimating impedance is as follows: Activate the control system of the PCS to output the electric voltage interconnected to the system voltage. In this case, the electric current which is output by the PCS is zero, and the electric voltage which is completely synchronized with the system is output. Next, substitute the initial value









Finally, turn off the configuration changeover section to stop the disturbance superimposition. Extract a pair which reached the maximum voltage from among


The sweep range values





Fig. 10 shows the flow chart of a sequence of operations.
3.3 Design of the compensator
The compensator is designed based on the estimated Grid-impedance. The resonance frequency

-
(4)
It turns out that an increase in resonance gain which causes unstable factors occurs in


-
(5)
4. Simulation results
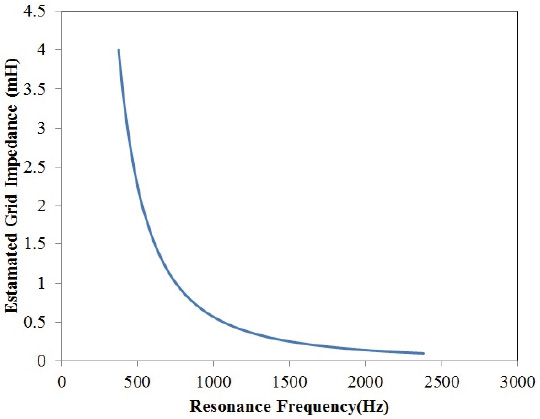
We implemented the algorithm for estimating the Grid-impedance on Matlab/Simulink, and to measure its accuracy, we estimated the impedance in combination with the circuit simulator implemented on Simscape. We estimated the Grid-impedance values


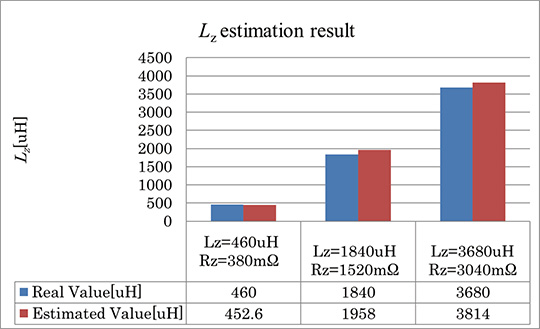
 estimation results obtained in the simulation
estimation results obtained in the simulation
Next, we designed the compensator based on the estimated impedance to confirm whether the control stability would be improved or not. For the values





-
(6)
To perform the current control system stability determination, we built the block diagram shown in Fig. 12 on Simulink and substituted the result of the equation (6) into the

Fig. 13 shows the open loop transfer functions of the current control system. The blue solid lines show the condition where the compensator

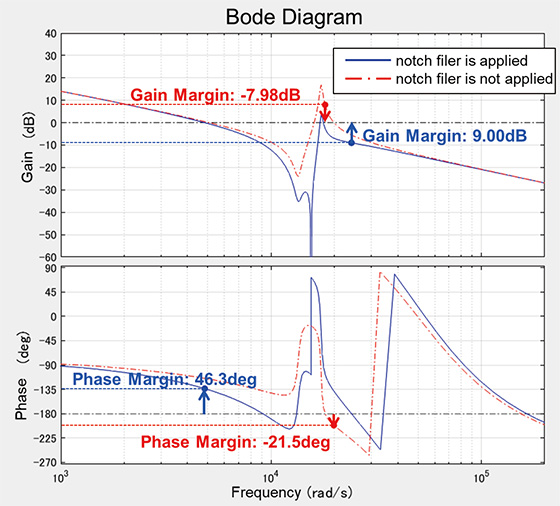
 = 460 ╬╝H)
= 460 ╬╝H)
5. Summary
In this paper, we showed an example of designing a compensator based on the method of estimating the Grid-impedance using the frequency sweep method and impedance for LC type and LCL type output filters of the PCS inverter. Designing the compensator in conformity with the Grid-impedance obtained after installing the PCS enables the downsizing of the ACL without impairing the stability.
Since this method enables enhancement of the stability of the control system simply by adding the impedance estimation section, the impedance suppression compensator section and one secondary compensator to the conventional configuration, it is possible to cope with the disadvantage of downsizing the ACL.
References
- 1)
- International Energy Agency. ŌĆ£Key World Energy Statistics 2017ŌĆØ. https://www.iea.org/publications/freepublications/publication/KeyWorld2017.pdf, (accessed 20180219).
- 2)
- J. Chen, F. Yang and Q. Han. Model-Free Predictive HŌł× Control for Grid-Connected Solar Power Generation Systems. IEEE Transactions on Control Systems Technology. 2014, vol. 22, Issue 5, p. 2039-2047, doi:10.1109/TCST.2013.2292879. https://ieeexplore.ieee.org/document/6720111
- 3)
- V. P. Singh, S. R. Mohanty, N. Kishor and P. K. Ray. Robust H-infinity load frequency control in hybrid distributed generation system. International Journal of Electrical Power & Energy Systems. 2013, vol. 46, p. 294-305, https://www.sciencedirect.com/science/article/pii/S0142061512005789
- 4)
- F. Huerta, D. Pizarro and S. Cobreces, LQG Servo Controller for the Current Control of LCL Grid-Connected Voltage-Source Converters. IEEE Transactions on Industrial Electronics. 2011, vol. 59, Issue 11, p. 4272-4284, doi:10.1109/TIE.2011.2179273. https://ieeexplore.ieee.org/abstract/document/6099608
- 5)
- J. Moriano, V. Bermejo, E. Bueno, M.Rizo and A. Rodriguez. A Novel Approach to the Grid Inductance Estimation based on Second Order Generalized Integrators. ECCE Cincinnati. 2017, p. 1794-1801, doi:10.1109/ECCE.2017.8096012. https://ieeexplore.ieee.org/document/8096012
- 6)
- M. Ciobotaru, R. Teodorescu, P. Rodriguez, A. Timbus and F. Blaabjerg. Online grid impedance estimation for single-phase gridconnected systems using PQ variations. Power Electronics Specialists Conference. 2007, p. 2306ŌĆō2312, doi:10.1109/PESC.2007.4342370. https://ieeexplore.ieee.org/abstract/document/4342370
The names of products in the text may be trademarks of each company.
















