FEM解析と逆問題的アプローチを使ったバラツキに起因する製品特性挙動の明確化
- 接触解析
- 熱応力解析
- データ分析
- 設計プロセス
- 逆問題的アプローチ
設計段階で想定していなかった問題が、試作段階で初めて問題となって発生することがある。その要因の1つに、実機評価で制御/観測困難なバラツキによる影響が挙げられる。バラツキの振れ方によって出力値やその変化特性が一定にならない現象は、ロジックをもとに検証していく“順問題的アプローチ”で真のメカニズムを捉えることができない。そのため、“逆問題的アプローチ”という多数の評価データから推論・検証するアプローチに着目し、熱衝撃下における3Dビジョンセンサの測距値変動を題材に、その有効性を検証した。
本検証では、まず非線形接触を考慮した熱応力解析により、熱衝撃下における力学的挙動と測距値変動量の推移を再現した。次に、入力値をバラツキ範囲で変動させて解析した多数のデータから、測距値変動量の傾向やバラツキの影響度を可視化・分析した。その結果、測距値変動に与える本質的な要因と熱衝撃下における締結部の挙動を明確化できた。また、実験計画法に適用型実験計画を使用することで、更に検証の効率化が可能なことを示し、逆問題的アプローチが開発期間の短縮や製品の価値創出に寄与する手法であることを確認した。
1. まえがき
当初想定された技術課題を設計上流で解決しても、試作評価時に想定外の問題が生じ、製品の要求仕様を満たせないことがある。その1つの要因として、実機評価時のバラツキが挙げられる。実機の評価系では制御/観測が困難なランダムに発生するバラツキ(寸法・物性バラツキ、組立バラツキ、測定環境など)によって入出力の因果関係が追えず、評価結果の再現性を得られない。そのため、問題の背景にあるロジックを設計者が推定しても、意図した条件下での実機評価および評価結果が得られず、ロジックに対する適切な妥当性検証が実施できない。特に複数のバラツキが影響し合う場合、実機評価結果から傾向を確認することは更に難しく、本質的な課題対策ができなくなってしまう。
前述の様なケースにおいて、少しでも論理的にメカニズムを解明するためにFEM解析を併用することが多いが、一般的なFEM解析においては、モデル作成段階でメカニズムの仮説を立てながら構築する、いわゆる“順問題的アプローチ”による検証を実行することになる。しかしながら、前述の通り、ランダム性により挙動を特定しきしれない現象に対しては、一部の現象を再現しているにすぎず、真のメカニズム再現には至らない。その結果、誤った理解・判断となり大きな手戻りや市場問題を招く可能性がある。
そこで今回、ランダム性が強く、メカニズム推定が非常に難しい課題に対して“逆問題的アプローチ”の活用を試みる。逆問題的アプローチは収集した多数の評価データを俯瞰した上で、データ起点でロジック推定する考え方であり、検証の網羅性や確度を担保しながら効率的に検証をすることができる。世の中にはFEM解析と逆アプローチで検証する事例は多数報告されているが1,2)、ランダム性の強いバラツキ全体の影響を解析した事例は公開されておらず、今回図1に示す3Dビジョンセンサの熱衝撃課題を題材に本アプローチの試行を実施した。

2. 熱衝撃による測距値変動と発生要因
2.1 異材締結を起因とした3Dビジョンセンサの課題
3Dビジョンセンサはパターンを対象物に投影して画像情報を取得・解析し、図2で示すプロジェクタ(投光)/カメラ(受光)モジュールの対応関係を特定することで測距値を算出している3)。また、測距原理や製品の要求制度から見積もると、μmオーダの構造的変動であっても、数mmオーダのセンシング特性に影響する。特に、周囲環境の温度変化による膨張・収縮が精度へ与える影響は大きく、ヒートショックのような急激かつ大幅な温度変動に対する測距精度の安定性確保のため、図3に示すような樹脂とアルミ合金のボルト締結を採用している。また、使用するモジュールの位置決め精度向上のため、位置決めピンを筐体側に設置する構造を採用している。
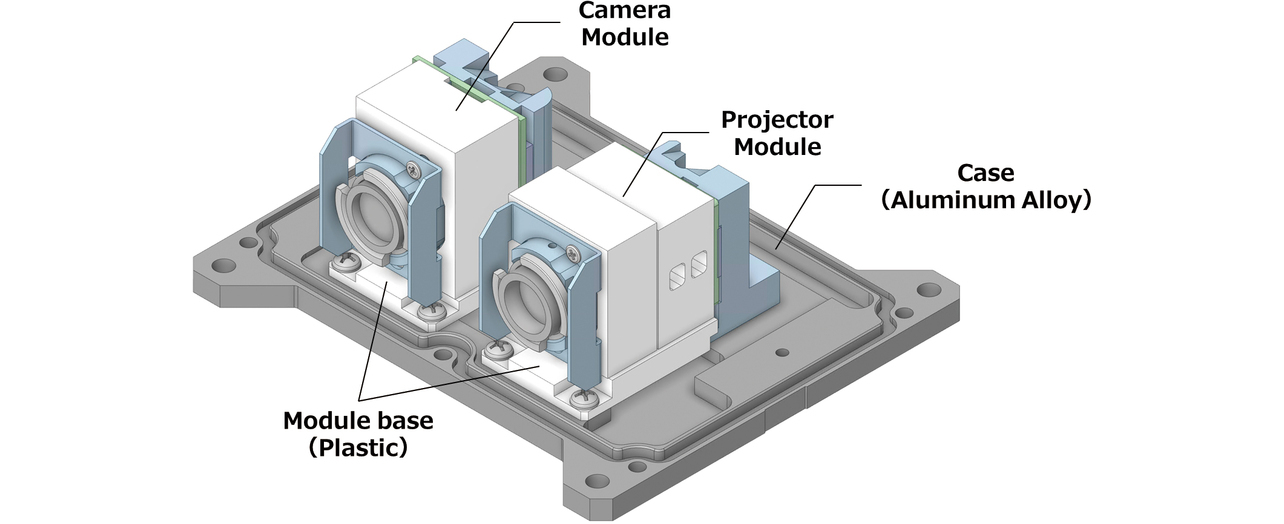
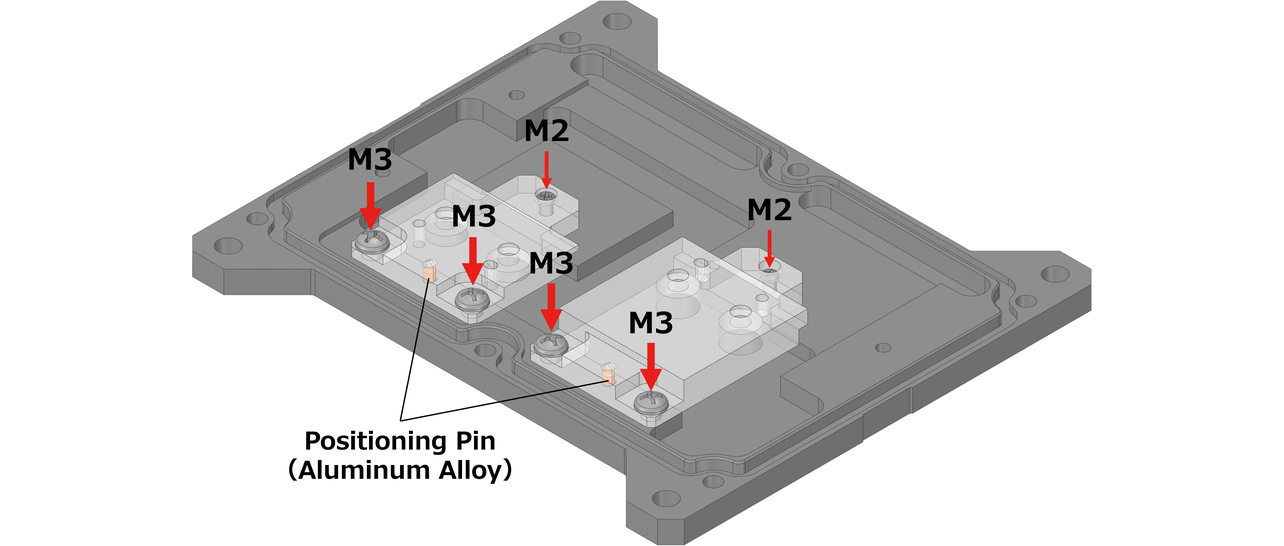
しかし、ヒートショックを想定した評価(以下、熱衝撃試験)において、初期サイクルで許容値を超える測距値変動が生じ、早急な対策が必要となった。まず原因分析のため、試験後の製品状態を確認すると、モジュール固定自体には問題無いレベルだが、樹脂とアルミ合金を締結しているM2ボルトのゆるみが確認された。一般に熱負荷を受ける異材締結では、その締結性能が低下しやすいことが知られている。既往の研究では、異材締結部に繰返し熱負荷を与えた場合、同材料で構成される締結体よりゆるみやすいことが実測・解析の双方から確認されている4,5)。そのため、3Dビジョンセンサのように構造物の微小変形や幾何配置が出力特性に影響する機器では、異材締結が温度変化時に影響を与えると考えられる。
しかし、同一サンプル/同一条件下でも測距値変動量が大きくバラつくことが確認され、再現性のある評価の実施ができなかった。その結果、ゆるみが測距値にどのように影響するのか、また、ゆるみ以外に測距値に影響を与える因子があるか等、十分な検証結果を得るには至らなかった。
2.2 熱負荷による締結力の変化
測距値変動の挙動明確化に向けて、まずは実際に確認されたボルトのゆるみが重要と考える。熱負荷時のゆるみの要因として、締結力低下による各接触面(ネジ部/座面部/被締結体表面)のすべりが挙げられる。そのため、簡単な力学モデルで熱負荷時の締結状態を表し、その傾向を推定する。
まず、接触面の状態を表す式として、クーロンの摩擦法則が知られている。クーロン摩擦では、作用する力に対して同等の静止摩擦力が反対方向に生じることで、力の釣合い(静止)状態を保つとされる。また、作用する力が閾値を越えると、一定の動摩擦力を伴いながらすべり状態へ移行する。すべり状態へ移行する単位面積あたりの力を限界静止摩擦応力σlim とすると、(1)式のように表すことができる。

μは接触面の静止摩擦係数、P+∆Pは各時点の接触面圧であり、Pは常温時の接触面圧、∆Pは温度変化による接触面圧増分である。締結体において、Pおよび ∆Pはその定義上、ボルトに発生する軸力FB および増分値 ∆FB と比例関係があると推定できる。そのため、組立(常温)時にゆるみが発生しない限り、∆FB が摩擦状態を決めるうえで重要になる。ここで、実際の締結状態について検討するため、ビジョン3Dセンサの異材締結部の構成を図4に示す。なお、各部材の物性値から、Material-I、Material-IIおよびボルトの線膨張係数α1, α2, αB の関係はα1≫α2, αB となる。組立時に締付トルクを与えるとボルトには軸力FB が発生する。この状態で温度変化を与えると、各部材は寸法/物性に従った熱膨張を開始する。しかし、各部材の熱膨張量が異なるため、結果的に自由な熱膨張を互いに妨げ、∆FB が発生する。
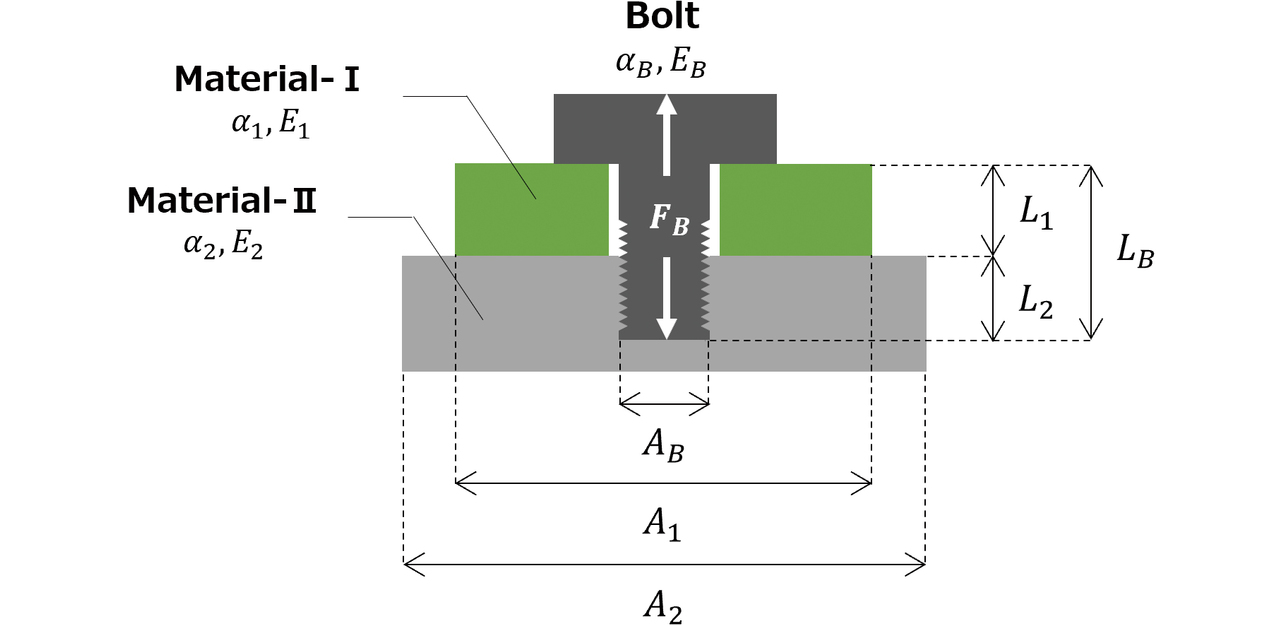
熱膨張量の差による ∆FB を推定するため、図5に異材締結部を簡略化した力学モデルを示す。ボルト軸方向について考えると、各部材は図に示すような膨張量となる。しかし、座面で膨張が妨げられるため、Material-IとMaterial-IIの変位量の和とボルトの変位量が一致した状態で力が釣合う。このとき、温度変化量 ∆Tに応じてボルトには熱応力による ∆FB が生じる。∆FB は軸方向の釣合い式を解くことで、(2)、(3)式の様に近似できる。


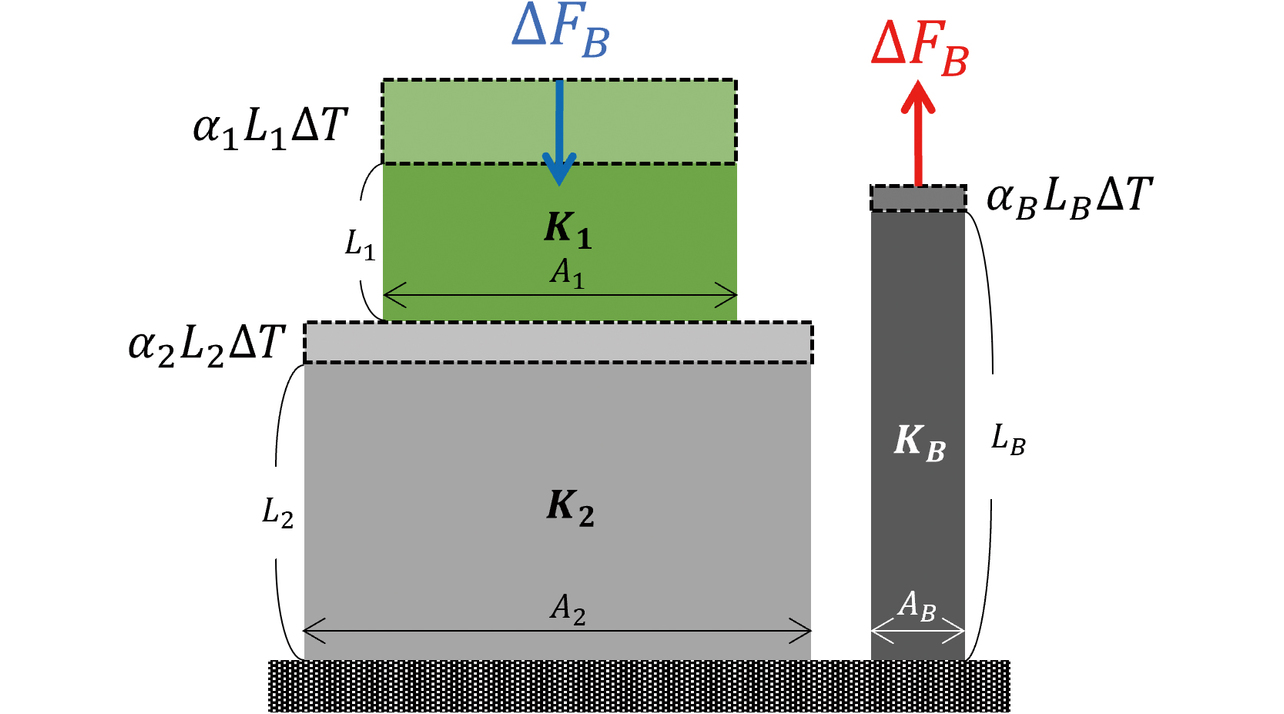
(2)式のKi (i=1, 2, B) は材料Ⅰ、Ⅱおよびボルトの軸方向剛性であり、Ei Ai /Li を置き換えた値である。なお、Ei は材料iのヤング率、Ai は材料iの断面積、Li は材料iの部材長さである。(2)式から、∆FB は低温時に負の値となり、ボルトの軸力および接触面圧が減少する。
一方、各接触面ではせん断応力が発生し、すべりを引き起こす力の主要因となる。せん断応力は ∆FB と同様に熱膨張量の差の影響を受けて増減するが、その値は ∆Tではなく、温度変化量の絶対値|∆T|に比例する。よって、∆FB 減少によるσlim の低下とせん断応力の増加が同時に進行する低温側で、各接触面のすべりおよびボルトのゆるみが生じやすい状態となり、測距値変動に寄与すると推定できる。
3. FEM解析による異材締結部の挙動再現
3.1 解析モデルの作成
順問題・逆問題的アプローチに関わらず検証に必要となる、現象再現可能な解析モデルについて述べる。熱衝撃による締結部の挙動を再現するため、非線形接触を考慮した熱応力解析を実施した。まず、形状モデル作成のため、光学部品の固定に寄与しない部品を削除し、詳細形状は簡略化した。また、2つの光学モジュールの内、測距値変動への影響の大部分を占めるプロジェクタ側モジュールのみを解析対象とした。図6に、メッシュ分割したモデルを示す。

次に、境界条件について説明する。熱衝撃試験を模擬するため、図7で示すように基準温度で各ボルトに軸力を、軸力印加後に試験条件と同一の10サイクルの温度履歴を与えた。また、FB と締付けトルク値Tqの関係はボルトの各寸法と摩擦係数から(4)および(5)式のように表される6,7)。


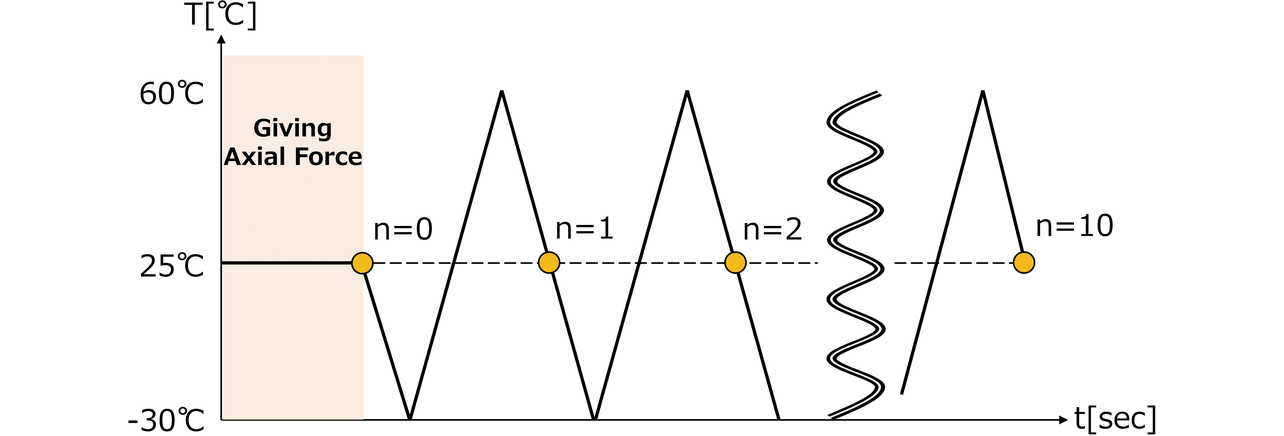
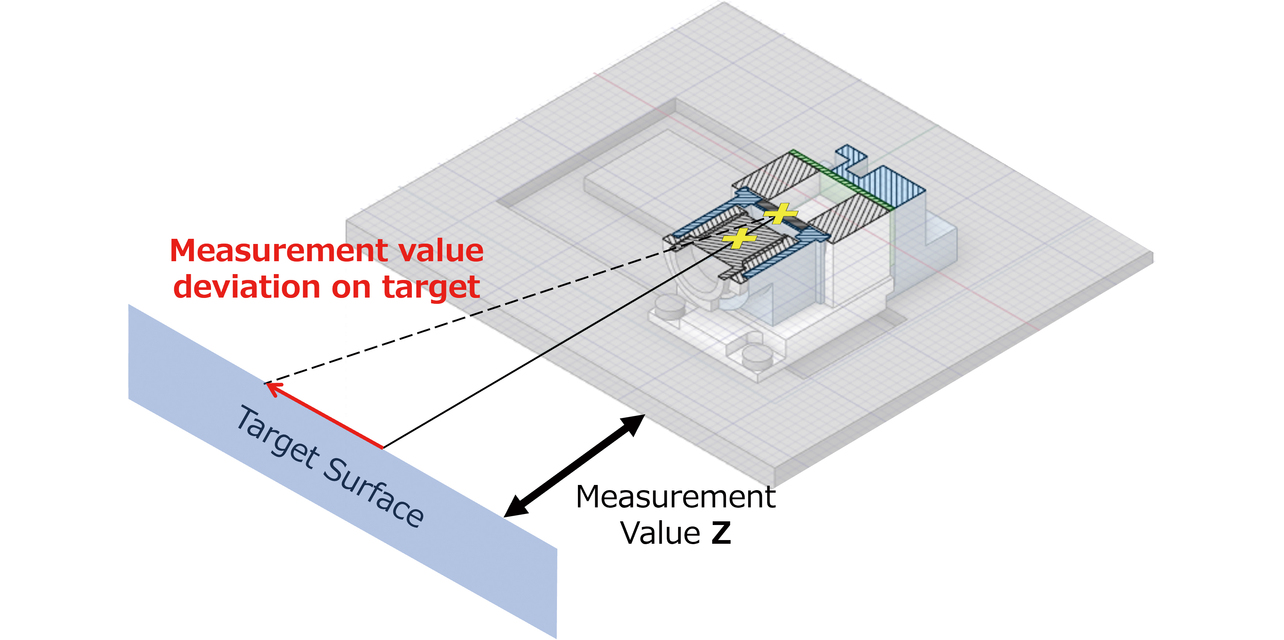
(4)式のμ1, μ2は、座面およびネジ山での摩擦係数である。また、β, γ, d2 , dw はボルトの寸法パラメータであり、ネジのリード角、ネジ山の角度、ネジの有効径、座面摩擦の等価直径である。(5)式は座面の等価直径を導出する式であり、ボルト座面接触部の外径d0と内径di から求められる。上式に締付トルク値とボルト寸法、摩擦係数を代入し、M2、M3ボルトの軸力をそれぞれ339N、713Nとした。なお、センサの測距値変動量 ∆Zは、図8に示すように各光学部品の幾何的な位置関係の変化によりターゲット上でのズレによって生じる。そのため、サイクル毎に取得した光学部品の変位量からターゲット上でのズレ量に換算し、ズレ量と各光学パラメータから ∆Zを算出した。
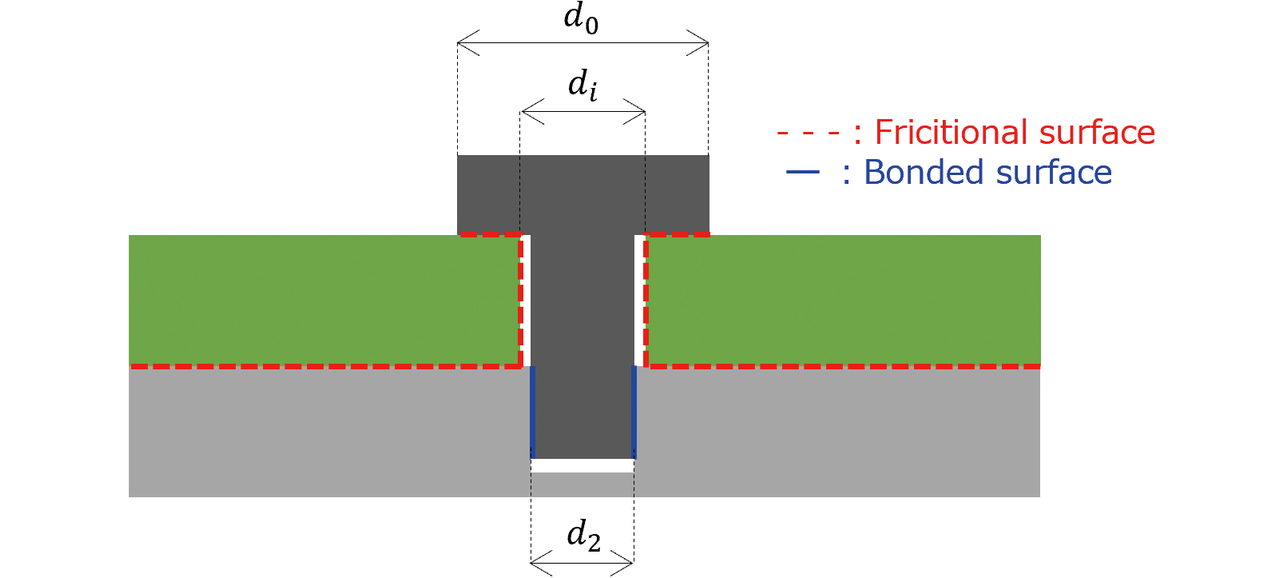
最後に、接触モデリングについて説明する。締結部の収束性悪化とモデル規模増大を防ぐため、図9に示すようネジ山部の詳細形状は再現せず、ネジ山相当部のみ固着、他の接触面は全てクーロン摩擦とした。また、接触アルゴリズムは収束性と精度の両立を図るため、拡張ラグランジュ法を用いた。なお、上述のモデル化および解析にはAYSYS Workbench Mechanical 2021R2を使用した。
3.2 解析結果とモデルの妥当性検証
図10に、実測とFEM解析から求めたセンサの測距値変動量の絶対値|∆Z|を示す。実測でサンプルに共通して確認された1サイクル目の|∆Z|が大きくなる傾向を、解析で捉えることができている。一方、解析では実測より過小評価する傾向にあるが、部品の温度分布/各種物性の温度依存性を考慮していないこと、固着定義によるネジ部剛性の過大評価、測距値変換式に含まれる誤差等が要因として挙げられる。
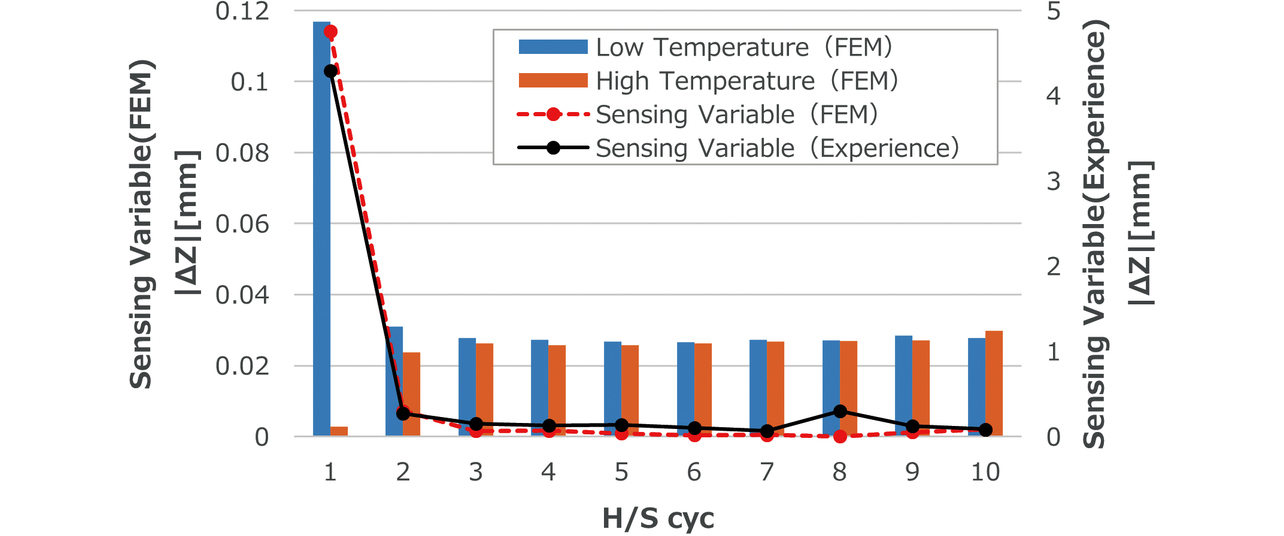
各棒グラフは1サイクル内における低温・高温過程での|∆Z|を示しており、1サイクル目では低温過程の|∆Z|が支配的となっている。また、図11に樹脂ベース-アルミ合金筐体間の接触面圧を示す。各温度で接触面圧に差が生じており、低温時は高温時より30%程度減少していた。これは、2.2項で述べた接触面圧増分 ∆Pの減少に由来した結果であるといずれも説明できる。また、2サイクル目以降|∆Z|が大きく減少する理由は、すべり発生による蓄積されたせん断応力の解放と推定される。図12に、サイクル間の最大せん断応力の差分を示す。1-2サイクル間では締結部周辺の最大せん断応力が最大1 MPa程度減少しているが、2-3サイクル間では1-2サイクル間程の顕著な低下は確認できない。よって、1サイクル目に作用していたせん断力が2サイクル目以降減少したことが分かる。
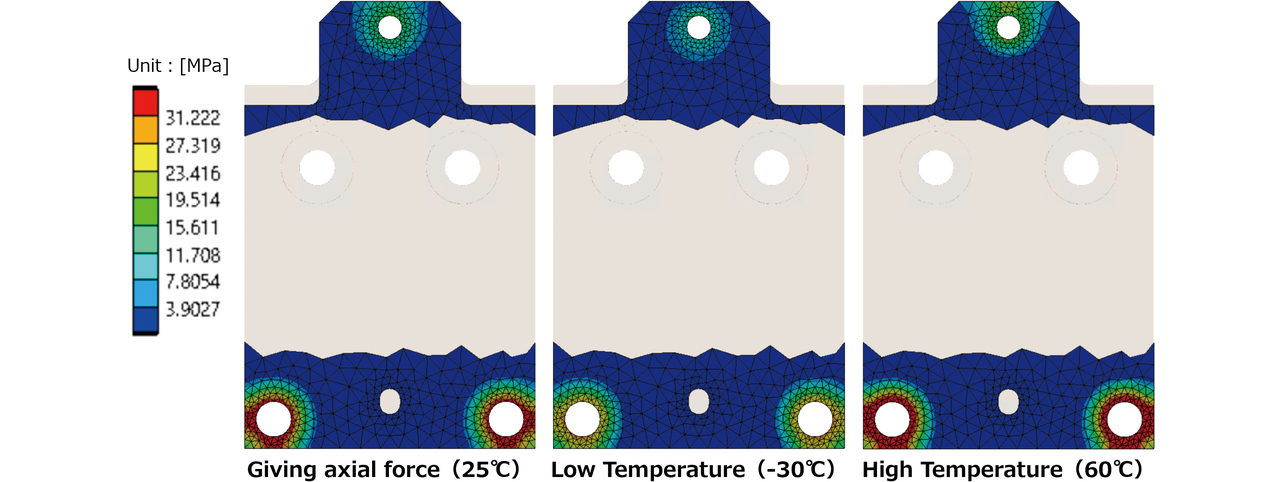
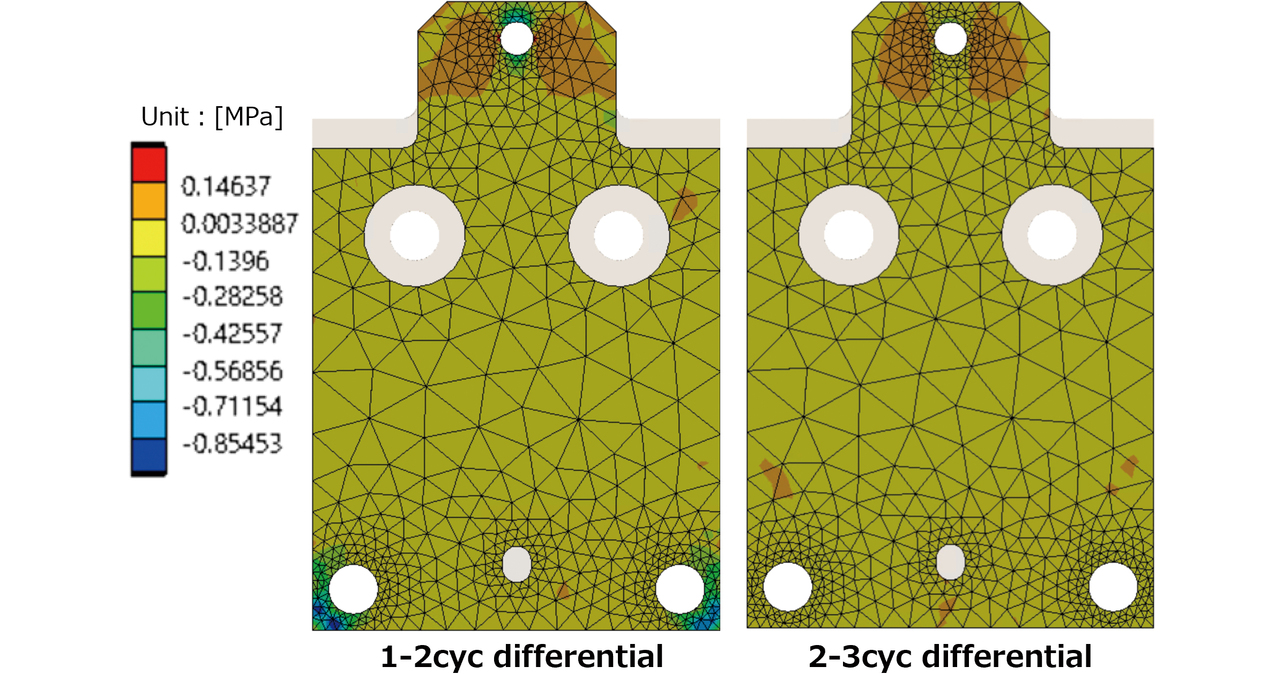
上述した実測における|∆Z|の定性的挙動や各物理量(接触面圧、せん断応力)の変化が理論と一致したことから、対象とする現象の傾向再現は可能と判断した。次章では、以上の現象に影響し得るバラツキについて検討する。
4. 逆問題的アプローチとFEM解析による検証
4.1 ロジック検証の具体的な流れ
逆問題的アプローチの具体的な流れについて説明する。まず、解析モデルの入力値となる部品寸法・物性・荷重条件等の一部を変数化し、実験計画法により各条件での解析結果を蓄積していく。本事例では同一条件・同一サンプルでも結果の再現性が取れないことと接触が重要であることから、荷重条件と組立時に累積する誤差の2種類に着目する。
まず、荷重条件に関しては各ボルトに生じる軸力を変動させる。一般的なトルク法による締結では、トルク値を厳密に管理しても軸力のバラツキが認められる。JISでは、同一トルクに対する軸力の最大値と最小値の比(締付係数)は1.4~3程度と記載されている8)。そのため、微小な変位・変形が重要となる本事例では、ネジ径に関わらず考慮すべきバラツキと考える。しかし、(4),(5)式に従って摩擦係数を変数化すると、パラメータの数が膨大になる点と、各ボルトの軸力を独立して扱えないという問題が生じる。そのため、図13に示す樹脂ベース-アルミ合金筐体を固定するM2/M3ボルトの軸力を直接変数化した。
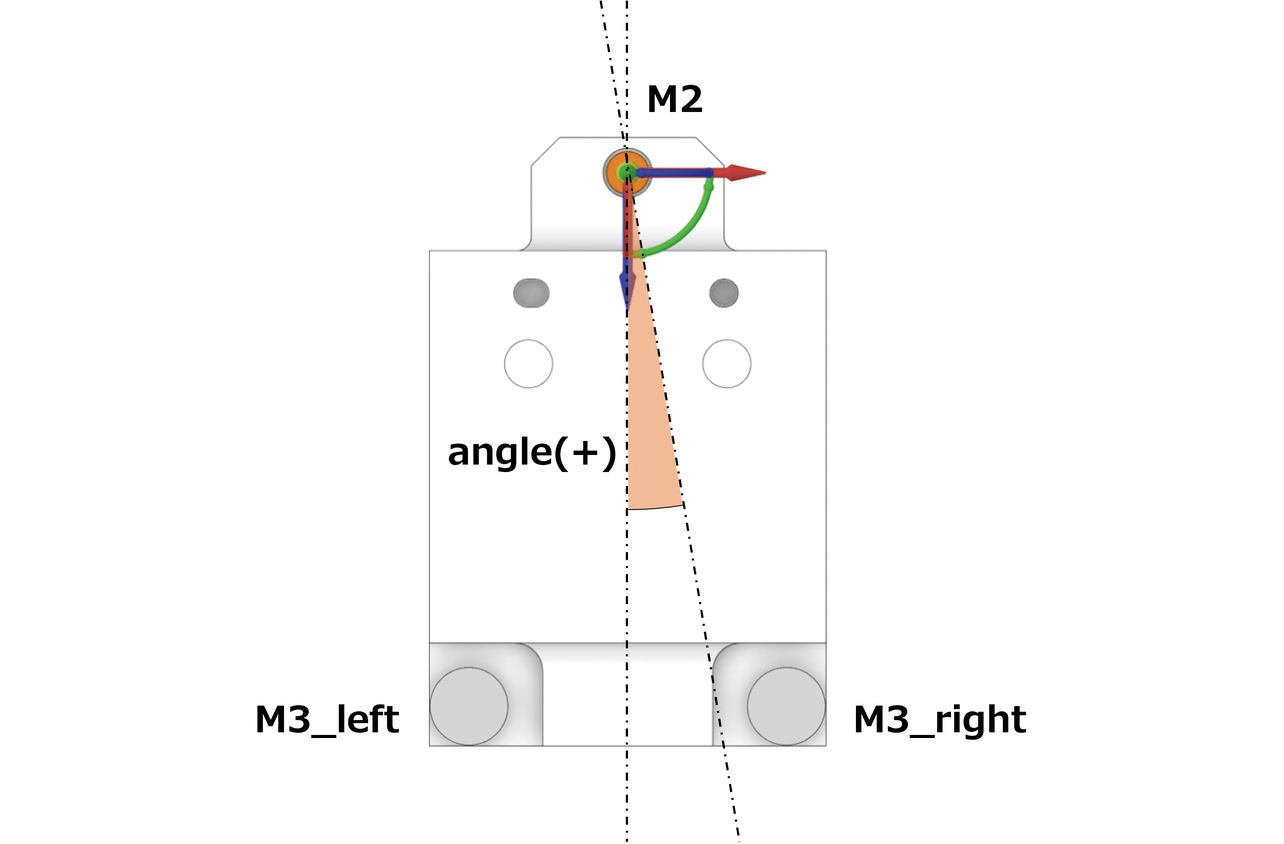
次に、組立時に累積する誤差に関しては樹脂ベースの実装位置を変動させる。先行研究では、ボルトや被締結体の各種公差も締結性能に大きく影響することが報告されている9-11)。樹脂ベース実装位置は図13中のM2ボルトを回転軸中心とする、樹脂ベースの回転ズレ量angleとして定義した。これは、angleを変動させることにより各固定構造(各ボルト座面、位置決めピン)の状態が連動して変化し、各部品(樹脂ベース、位置決めピン、ボルト)の寸法を1つずつ変数化するよりも、効率的な検証が可能なためである。
実測・解析ともに1サイクル目が支配的かつ重要であることから、応答変数は1サイクル目の ∆Zとした。表1に設定した変数とレンジを示す。実験計画法にはユーザが実験回数を指定可能であり、設計空間を満遍なく探索可能なラテン超方格法を使用した。取得するサンプル総数は250とし、80%は応答曲面生成用の学習用に、残り20%は精度評価用のサンプルとした。なお、解析モデル上で定義した説明変数の自動更新・解析実行、および実験計画法の詳細設定にはmodeFRONTIER 2022R3を使用した。
| Variable | Category | Range |
|---|---|---|
| M3_right | Explanatory variables | 374N~713N |
| M3_left | Explanatory variables | 374N~713N |
| M2 | Explanatory variables | 180N~339N |
| angle | Explanatory variables | -0.29°~0.29° |
| ∆Z | Response variables | \ |
解析と実験計画によるサンプル取得完了後、傾向の可視化や寄与度分析等により、特徴的な領域や着目すべき評価条件を選定する。但し、この時点では解析結果は単なる数値データ群として扱い、物理的な解釈は入れずに検討する。最後に、選定した各評価条件での解析結果を確認し、物理的な解釈を加えることで適切なロジックを推定していく。
4.2 データ取得結果とロジック推定・検証
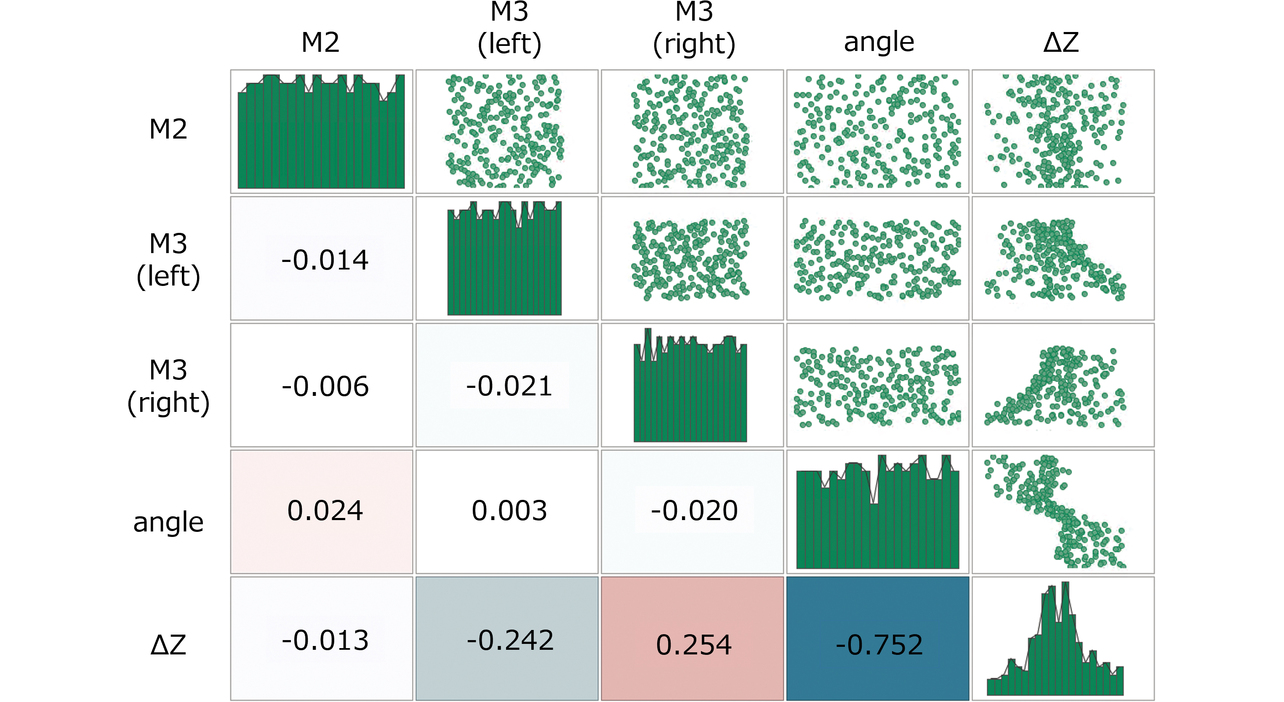
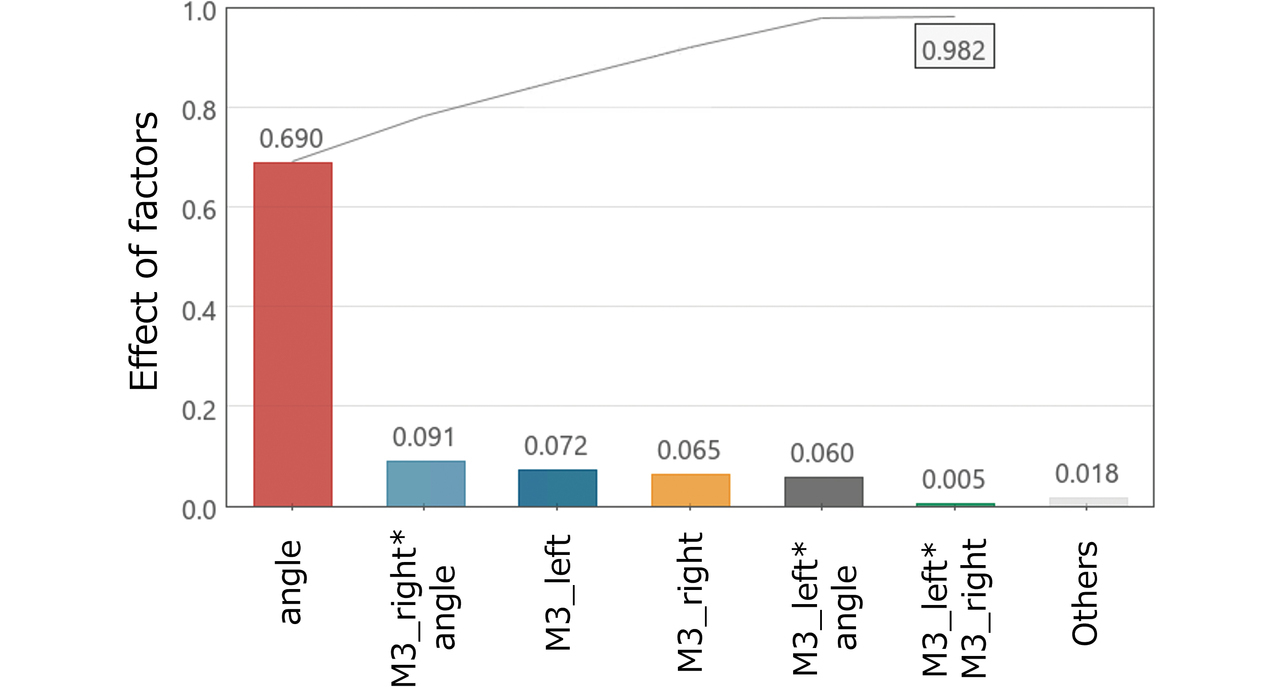
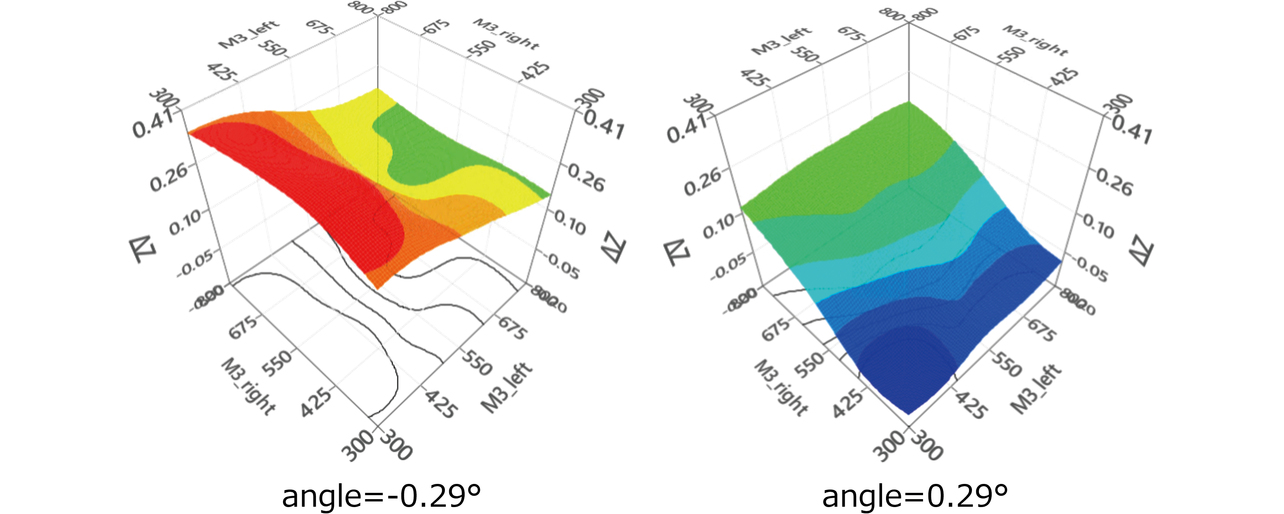
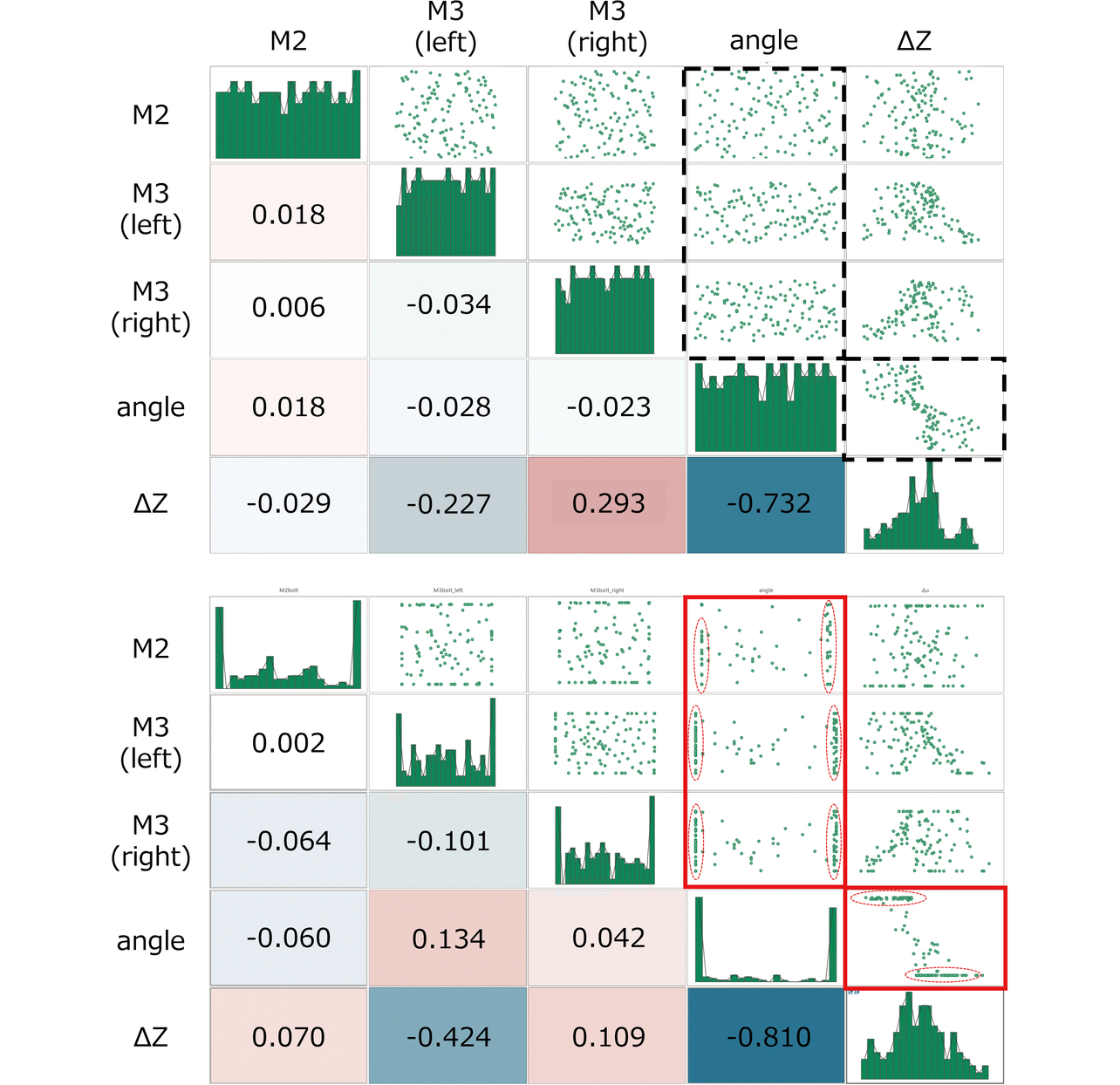
図14および図15に、サンプリングと寄与度分析結果を示す。angleの相関係数および寄与度が最も高く、M2が最も低くなった。また、M3_rightとM3_leftの相関係数や寄与度は同程度の値を示しており、散布図から両者の傾向が左右対称であることも確認できる。傾向を詳細に可視化するため、図16に作成した応答曲面を示す。なお、比較した複数手法の中で決定係数R2が0.95と最も高くなり、サンプリング点間を放射基底関数で補間するRBFで曲面を作成した。angle=0.29°, -0.29°の応答曲面から、angleにより∆Zの方向が規定されていることが分かった。また、angle>0ではM3_rightが、angle<0ではM3_leftが因子として有意になることを確認できた。
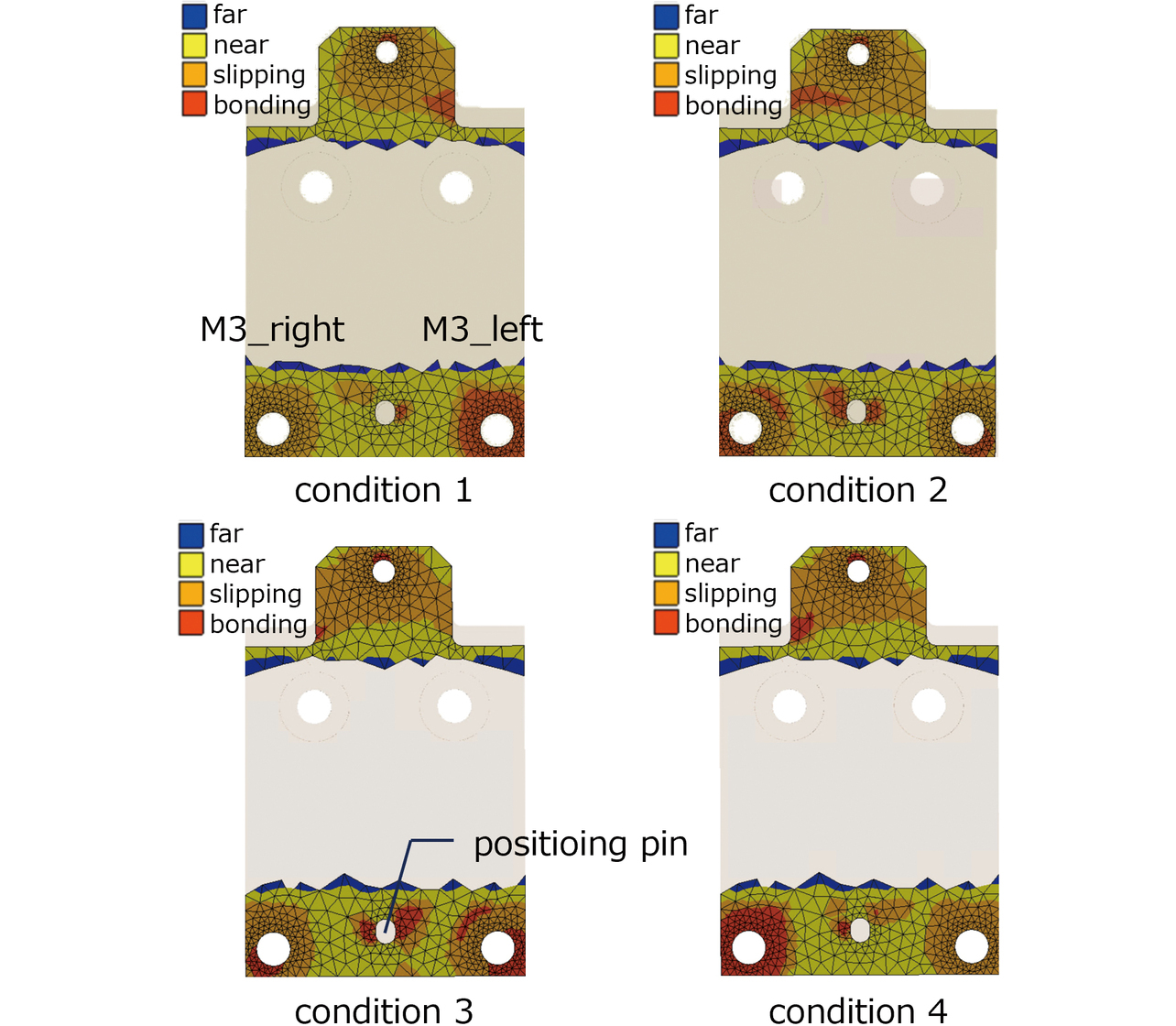
分析結果を参考に、表2に示した4条件を再計算した。内訳は、∆Zの絶対値が大きい2条件とM3_right/M3_leftの値を反転させた2条件の計4条件である。図17に、各条件での樹脂ベースと筐体間の接触状態分布を示す。但し、底面視表示であるため、左右反転していることに留意されたい。まず、angle=0.29°の状態でM3_right、M3_leftの値が反転している条件1と条件2で比較する。条件1ではM3_rightの低下で周辺領域が全てすべり状態となる一方、条件2ではM3_left周辺領域に固着状態が残存した。次にangle=-0.29°の場合、条件4のM3_left周辺領域が全てすべり状態となったが、条件3ではM3_right周辺に固着状態が残存し、angle=0.29°と正反対の挙動となった。理論に従えば、軸力低下によりすべりのリスクは高くなるため、条件2と条件3で特異な現象が起こったと推定できる。また、条件2と条件3の特有の事象として、位置決めピン周辺で強い固着状態が生じていることを確認できる。
| Variable | Condition 1 | Condition 2 | Condition 3 | Condition 4 |
|---|---|---|---|---|
| M3_right | 374N | 713N | 374N | 713N |
| M3_left | 713N | 374N | 713N | 374N |
| M2 | 180N | 180N | 180N | 180N |
| angle | 0.29° | 0.29° | -0.29° | -0.29° |
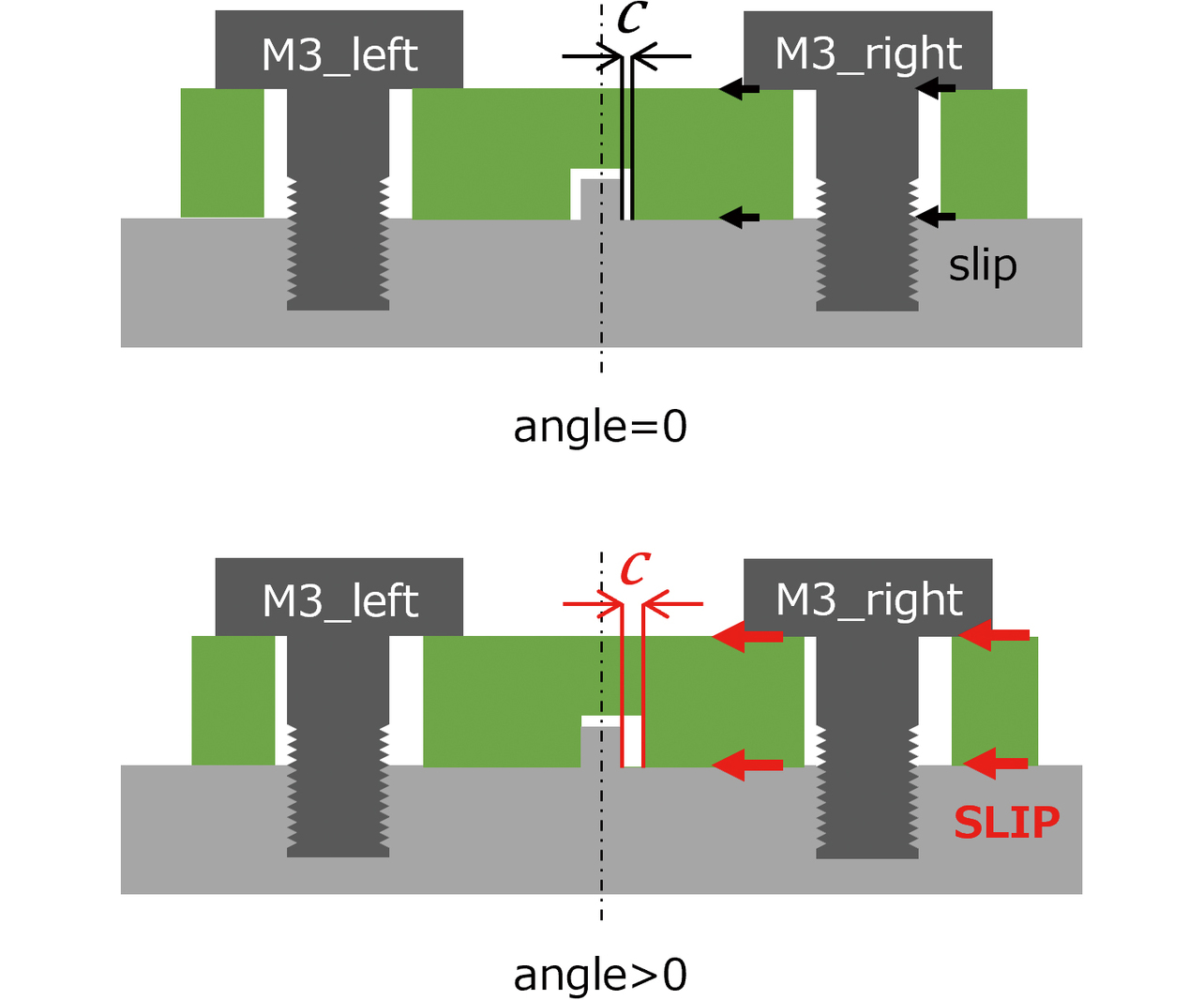
上述の挙動を示す要因として、位置決めピン部のクリアランスが推定される。図18に、樹脂ベース前方部の構成を示す。組立バラツキによりangle>0となった場合、位置決めピン部のクリアランス量には図に示すような左右差が生じる。angle>0かつM3_rightが低い場合(条件1)、理論および解析結果から、低温時には左側のM3ボルト周辺が固着、右側のM3ボルト周辺がすべり状態となる。そのため、右側のM3ボルト周辺の樹脂ベースが、右側から左側に向かってすべるような挙動となる。このとき、angle>0では、すべり方向に対するクリアランス量cが大きいため許容すべり量が増加する。その結果、温度変化前後でモジュールおよびモジュール内部の光学部品にもズレが生じ、∆Zが大きくなったと推定される。一方で、angle>0かつM3_leftが低い場合(条件2)では、cが極端に小さくなるため、∆Zが小さくなると推定される。条件3と条件4についても、cとボルト軸力値の対応関係が条件1/条件2と反転したのみであり、同様の挙動で説明が可能である。
以上の仮説の妥当性確認のため、条件2のcを変化させた際の ∆Zの変化を検証した。具体的には、位置決めピンの外径D(基準寸法2 mm)を0.02 mmずつ小さくしてcを増加させていった。その結果を、図19に示す。条件2の状態であっても、Dが小さくなる(cが大きくなる)に従って ∆Zが大きくなることが分かった。よって、組立時のcの増減によって樹脂ベースのすべり量が変化し、∆Zに影響を与えたと結論付ける。
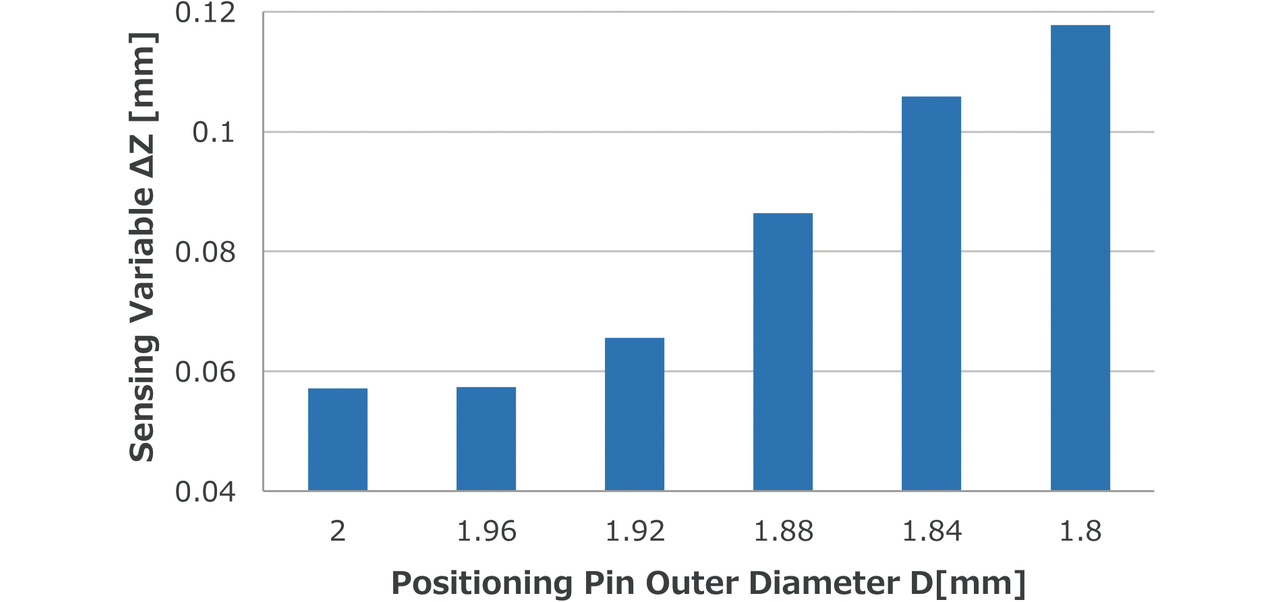
ここまでの検討結果から、最終的な結論として ∆Zが大きくなる要因は以下2つである。
- すべり方向に対する位置決め部のクリアランス量c
- クリアランス量cとM3ボルト軸力の交互作用
また、∆Zを抑える条件は以下のいずれかである。
- クリアランス量cの低減/適正化
- M3ボルトもしくは全ボルトの軸力向上
但し、cは製品構造上、直接測定ができず、各部品の寸法公差および組立手順により容易に変化する値である。また、軸力はボルト外径の小ささから超音波軸力計やひずみゲージ等での測定が難しく、(4)式で示したように表面状態や各種寸法で変化するため、cと同様に不安定なバラツキである。そのため、∆Z抑制に向けては生産工程ではなく、位置決め設計や光学モジュールの材質変更のような設計観点での対策が課題となる。
4.3 逆問題的アプローチの効率化
逆問題的アプローチの核である実験計画法では、可能な実験数(もしくは時間)と精度のトレードオフ性という大きな課題がある。設計プロセス内での活用を考えると、検証行為に費やせる時間や工数は限られるため、最小限のサンプルで精度を担保し、有益な情報を最大限得ることが期待される。また、1回あたりの検証サイクルが早くなれば、パラメータを変更/増加による追加検証や複数の構造案の比較なども可能となり、設計はより充実したものとなる。しかし、未知の設計空間に対して事前に適切なサンプル数や実験計画法を定義することは難しく、過剰なサンプリングによる工数増加、サンプル不足による精度低下といった問題を招く。
以上の問題を解決する手法として、適応型実験計画を本事例で検討した。適応型実験計画は予めサンプルの取得計画を決めず、サンプル取得と設計空間の評価を内部で繰り返すため、少ないサンプル数での精度向上が期待されている12,13)。本稿では、適応型実験計画の1種であるMACK(多変量適応型交差検証Kriging)14)に着目した。MACKは、はじめに設計空間内を粗くサンプリングした後、応答曲面の交差検証を内部で実行し、不確実性の高い領域をリサンプリングする手法である。本稿では、MACKの活用による効果検証をするため、ラテン超方格法との比較を実施した。
図20に、各手法でのサンプリング結果を示す。ラテン超方格法では設計空間内を一様にサンプリングする一方、MACKではサンプリング領域の偏りが確認できる。特に、4.2項で寄与が高いと判断されたangleの上下限値付近を集中的にサンプリングしており、∆Zが変動しやすい領域を集中探査したと推測できる。また、MACKを適用することで目標精度に到達するまでのサンプル数が100から40、計算時間に換算すると25 hから10 h程度まで低減した。以上の結果から、MACKは設計空間内の特徴的な領域を効率的に探索することが可能であり、逆問題的アプローチによる検証期間の短縮に大きく貢献する手法であることを確認できた。
5. むすび
実機評価における制御/観測不可能なバラツキにより、製品特性挙動の解明が難しい問題に対して、FEM解析と逆問題的アプローチを使った手法に着目した。本稿では、熱衝撃試験下における3Dビジョンセンサの測距値変動を対象とし、上述の手法による検証を実施した。その結果、実機で確認されたM2ボルトのゆるみは測距値変動に寄与せず、“M3ボルトの軸力低下時における、樹脂ベースすべり方向に対するクリアランス量が影響する”というロジックを明確化できた。また、サンプリング効率向上のため実験計画法にMACKを採用することで、本事例では最大60%程度N数を削減し、効率化に向けた有効な手法であることを実証した。
複数のバラツキが結果に影響する場合、適切なロジック推定および評価条件の設定が課題となり、順問題的アプローチによるロジック検証は困難を極める。今回、このような課題に対して逆問題的アプローチを活用することで、逆問題的アプローチが課題解決に有効であると同時に、設計者が無暗に試行錯誤を繰り返すことなく、限られた工数の中でロジック検証できることを示した。この成果は様々な技術課題に対して適用可能であり、開発期間の短縮および、より早いサイクルで製品の市場投入の実現に繋がる技術である。
今後の課題として、精度および効率の向上が挙げられる。まず、精度の観点として、樹脂ベースの詳細物性考慮による熱応力解析の精度向上が挙げられる。樹脂は金属材料に比較して温度依存性や成型過程に起因した異方性の影響が大きく、急速な温度変動の影響も大きいと考えられる。そのため、TMA(熱機械分析)等の各種試験により詳細な樹脂の物性値を取得し、解析へ反映することが必要である。一方、効率の観点に関しては、サンプル数の自動決定が挙げられる。本事例ではMACKの効果検証のため、筆者がサンプル数を予め指定してサンプルを取得した。しかし、本来はサンプル数もユーザが事前に決めるのではなく、一定精度を満たした段階でサンプリングを終了する状態が望ましい。そのため、最大実験可能数のみを制約として、狙った精度実現する考え方や具体的な手法を構築する必要がある。
以上、熱応力解析の精度向上とサンプリング効率向上により、発生事象や製品挙動に対する解析能力を更に高め、ロバスト性の高い設計を実現する設計技術の構築を目指す。
参考文献
- 1)
- 池田正哲, “商品開発における技術要素間のトレードオフを解消するバランス設計手法の革新,” OMRON TECHNICS, vol. 52, no. 1, pp. 105-110, 2020.
- 2)
- 佐藤一樹 他, “機械学習を用いた電力変換機器の最適化設計プロセスの実証,” OMRON TECHNICS, vol. 54, no. 1, pp. 101-106, 2022.
- 3)
- 太田潤 他, “小型・軽量かつ耐環境性を備えたロボットハンド搭載型3Dセンサの開発,” OMRON TECHNICS, vol. 54, no. 1, pp. 60-65, 2022.
- 4)
- 沢俊行 他, “繰返し温度変化を受けるボルト締結体のねじの回転ゆるみメカニズム,” 山梨講演会講演論文集(日本機械学会), 2007, pp. 149-150.
- 5)
- 小林光男 他, “熱負荷を受けるねじ締結体の軸力挙動へ及ぼす被締結体の影響,” 日本機械学会東北支部秋季講演会論文集, 2016, vol. 52.
- 6)
- 晴山蒼一, “トルク法によるねじ締付けにおける軸力管理に関する研究:第1報, ねじ軸力分布の信頼限界について,” 日本機械学会論文集C編, vol. 53, no. 495, pp. 2373-2379, 1987.
- 7)
- 小林光男, “ねじ締結体の基礎知識,” 精密工学会誌, vol. 81, no. 7, pp. 619-622, 2015.
- 8)
- 日本産業規格. JIS B 1083, 2008.
- 9)
- 岡田学 他, “ボルト締結における座面圧分布について:座面の角度偏差が及ぼす影響,” 日本機械学会論文集C編, vol. 70, no. 699, pp. 3324-3330, 2004.
- 10)
- 福岡俊道 他, “ねじ部品の形状誤差を考慮したトルク法の締め付け精度の改善,” マリンエンジニアリング, vol. 51, no. 2, pp. 238-245, 2016.
- 11)
- 笠井周 他, “中空ねじ締結体の締結状態に及ぼすナット座面制度の影響:第1報, ナット座面精度と中空ボルトの軸方向ひずみ分布との関係,” 日本機械学会論文集C編, vol. 61, no. 583, pp. 1136-1142, 1995.
- 12)
- 上野哲朗 他, “機械学習によるX線スペクトル計測の効率化,” 表面と真空, vol. 62, no. 3, pp. 147-152, 2019.
- 13)
- K. Shimoyama et al., “A Kriging-Based Dynamic Adaptive Sampling Method for Uncertainty Quantification,” Trans. J. Soc. Aeronaut. Space Sci., vol. 62, no. 3, pp. 137-150, 2019.
- 14)
- ESTECO S.p.A. “modeFRONTIER.” https://engineering.esteco.com/modefrontier/(Accessed: Oct. 1, 2023).
本文に掲載の商品の名称は、各社が商標としている場合があります。














