制御プログラム解析とデータ解析の統合による製品不良の要因特定手法の提案
- プログラムスライシング
- 相互情報量
- 要因解析
- 有向グラフ
- PLC
近年はIoTの普及に伴い、Factory Automation（FA）領域の製造現場において、センシングデータや制御データを収集して、製品不良の要因を解析する事例が増加している。しかしながら、FA製造現場で収集される制御データは、複数工程が同期制御されるため、ある制御データが別の制御データに連動して変化することになり、結果として独立性が低くなるという特徴がある。このため、従来手法では、多くの要因候補が選択されてしまい、真因にはたどり着けない場合がある。
本稿では、プログラムの依存関係を抽出するプログラムスライシング技術を適用し、複数工程処理と同期制御の情報を持つプログラマブルロジックコントローラ（PLC）の制御プログラムから知識情報を抽出してデータ解析に統合することで、制御データと制御プログラムから製品不良の要因を特定する手法を提案する。また、従来手法では要因特定出来なかった事象について、実験用包装機を用いて、提案手法が有効であることを確認した。
1. まえがき
近年はIoT（Internet of Things）の普及に伴い、FA領域の製造現場において、センシングデータや制御データを収集して、製品不良の要因を解析する事例が増加している1,2）。しかしながら、品質管理分野で特性要因図3）を用いてドメイン知識情報を整理しているように、収集したデータの解析だけでは適切な要因を特定するのは難しい。
従来は、1つのアプローチとして、不良やトラブルが発生した場合に決定木の重要度による要因解析を行うという方法が効果的とされていた4,5）。しかし、制御データから決定木の重要度を算出しただけでは、多くの要因候補が選択されてしまい、真因にはたどり着けないケースが存在する。これは、データのみでは複数工程のデータが同期されており、確率論的独立性が低くなるためである。
FA領域では、稼働率・性能・品質から算出される設備総合効率6）を向上させるために、主に物理的な組み立て・加工などを行うプロセスを自動化し、高生産能力と高品質な生産を高稼動率で運用する。よって、FA制御技術は、高生産能力を目的とした複数工程の並列化と高品質を目的とした高精度な同期制御等を特徴とする。この結果、製造現場で収集される制御データは、複数工程が同期制御されるために独立性が低いという特徴がある。
本稿は、複数工程処理と同期制御の情報を持つPLCの制御プログラムに着目し、制御プログラムから知識情報を抽出して、データ解析に統合することを提案する。提案手法では、プログラムスライシング技術を適用し、PLC制御プログラムから生成された変数依存グラフと、制御データから生成された構造変化グラフを合成することによって、制御データの独立性を高めることで要因推定の精度を向上させる。また、提案手法により、従来手法では要因特定できなかった事象について、実験用包装機を用いて実証する。
2. 従来手法とその課題
本章では、制御システムにおいて複数工程が同期するために制御データの確率的独立性が低い課題について、本稿の対象システムである包装機の振る舞いを用いて説明する。
2.1 対象システム
対象システムとなる実験用包装機について、図1に紹介する。
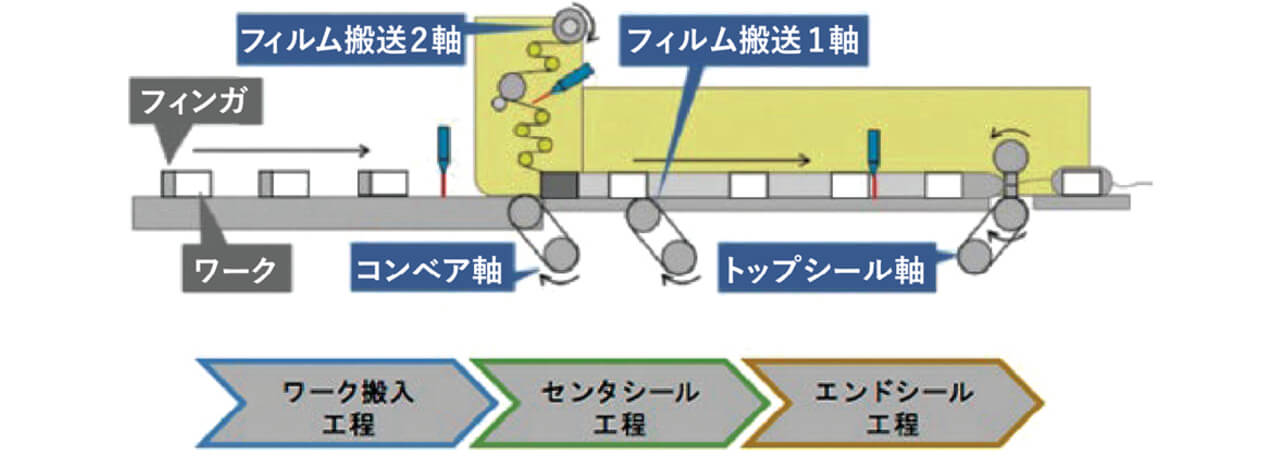
本稿で取り扱う包装機は、樹脂製フィルムによって製品を包装する横型ピロー包装機である。PLCは4つのサーボモータの同期制御を行うことで包装を自動化している。本包装機では、フィンガによってワークを送り出すワーク搬入工程、センターシール工程、エンドシール工程の3工程を経ることでワークを枕状に包装する。4つのサーボモータは、ワーク搬入を担うコンベア軸と、センターシール工程を担うフィルム搬送1軸、フィルム搬送2軸、エンドシール工程を担うトップシール軸として制御され、それぞれのトルク・速度・位置信号は制御データとして収集される。なお、これらの制御データから製品不良の要因を解析することにより、センサ追加が不要になるメリットがある。
2.2 従来手法
従来の要因特定手法は以下のステップから構成される。
- 1．
- 制御データから特徴量を算出する。
- 2．
- すべての特徴量から決定木の重要度を算出する。
- 3．
- 重要度の高い特徴量に該当する状態を要因として特定する。
まず、制御データから特徴量を算出する概念を図2に示す。
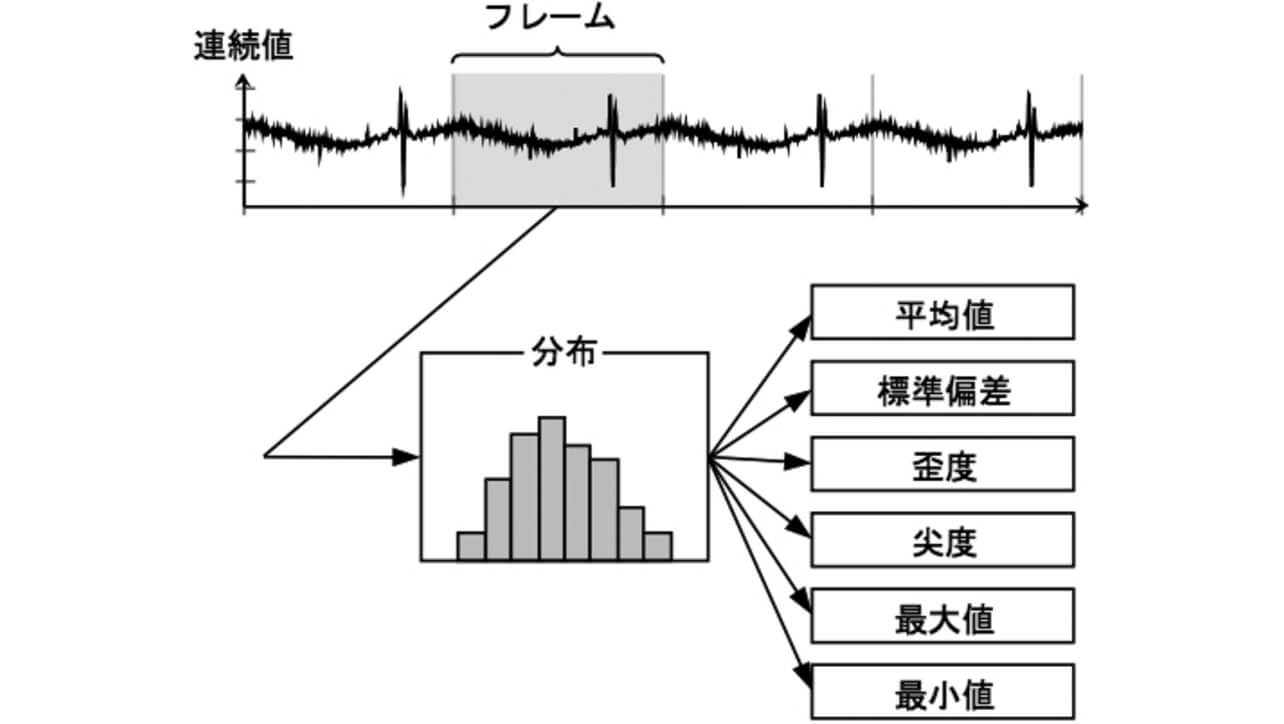
ここでは、収集した制御データをフレームと呼ぶ製造の周期単位で区切り、平均値や標準偏差などの複数の統計量を特徴量として算出する。前述の包装機の例では、ワークを包装する単位がフレームとなる。
次に、すべての特徴量の重要度を算出し、重要度の高い特徴量を選択する。この特徴量に該当する状態を要因として特定していた。決定木は、木構造を用いて分類や回帰を行う機械学習の手法の一つである。ここで使用する重要度は、各特徴量で正常と異常を判別したときの判別前後のGini係数の減少量であり、値が大きいほど正常・異常を判別する変数として適していることを表す。
2.3 従来手法の課題
従来手法で使用される特徴量データの散布図の一例を図3に示す。
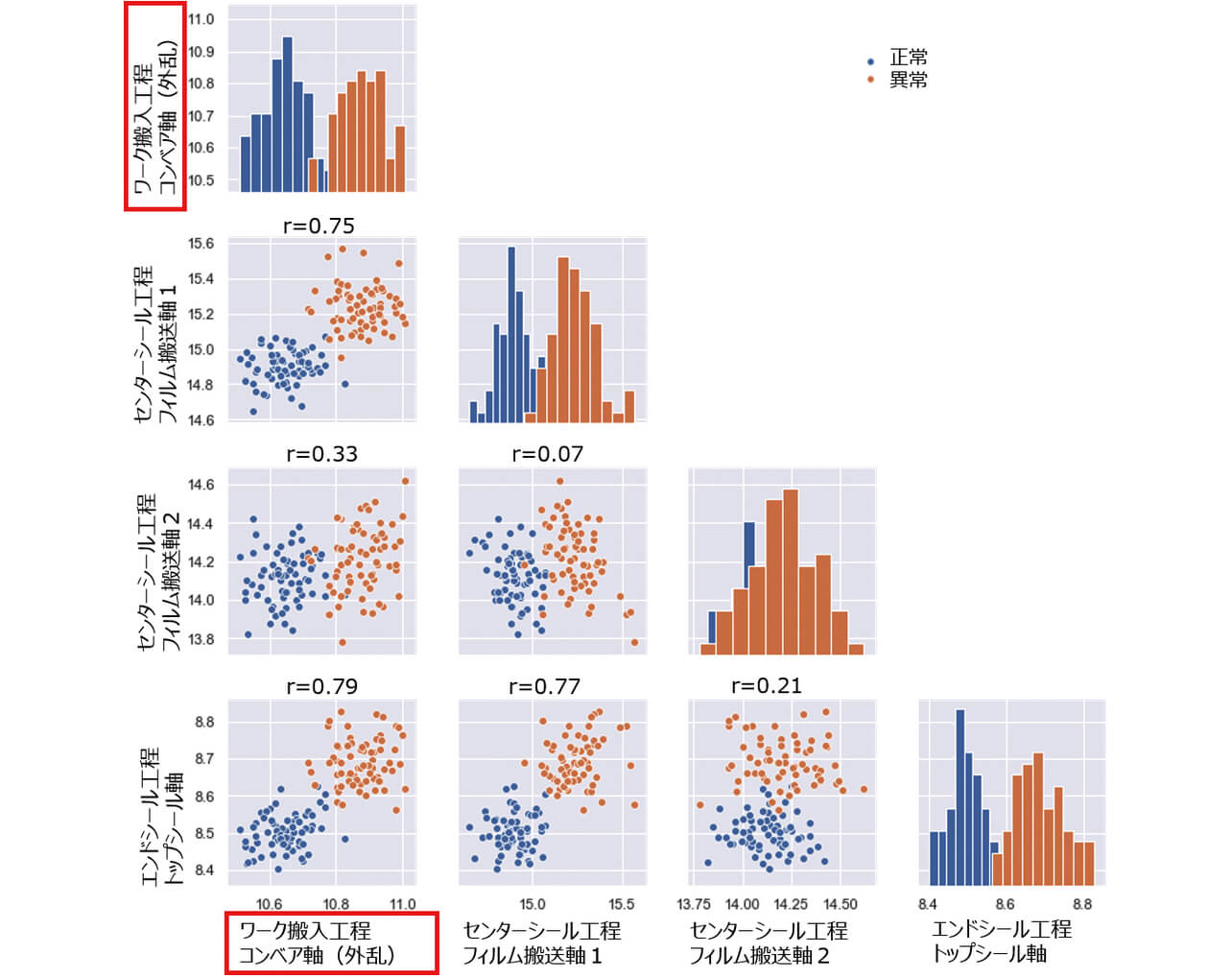
この散布図は、4つのサーボモータの制御データから算出した特徴量であるトルク平均値について、正常に包装したものと、疑似異常としてコンベア軸に外乱を与えたものの関係性を表す。本包装機は複数工程が同期されているため、ワーク搬入工程のコンベア軸に与えられた外乱が、後工程の各サーボモータのトルクに反映されている。特にフィルム搬送軸1とトップシール軸はコンベア軸との相関係数がそれぞれ0.75、0.79と高い関係性を示している。これはPLCが高精度な同期制御を行っているために、制御データ間の独立性が低くなることを示している。
これらの特徴量について、決定木の重要度を算出し、要因特定を試みた結果を表1に示す。
| 特徴量 | 重要度（順位） |
|---|---|
| トップシール軸 トルク 最小値 | 0.129（1） |
| トップシール軸 位置 最小値 | 0.126（2） |
| トップシール軸 トルク 最大値 | 0.112（3） |
| コンベア軸 トルク 平均 | 0.074（7） |
ここでは、決定木のアルゴリズムとしてRandomForestを使用し、重要度の高い3つの特徴量と本来の要因を示す特徴量の重要度を記載している。この例では、コンベア軸の外乱はコンベア軸トルクに現れることが想定され、重要度は48種類の特徴量の中で7番目となっている。比較的高い値を示しているが、後工程のトップシール軸の特徴量の重要度の方が高くなっており、正しく要因を特定出来ていない。これは独立性の低いデータを含む制御データ群から算出された決定木重要度は、要因特定に適さないことを示している。
3. 提案手法
3.1 提案手法の概要
本稿では、独立性の低いデータを分離するアプローチとして、PLC制御プログラムから工程と同期制御の情報を持つ制御フローを抽出し、制御データの関係性を制御フローに合成することでデータの独立性を高めて、上流工程の要因を特定する。提案手法は以下のステップから構成される。
- 1．
- 制御プログラム解析（プログラムスライシング）により、制御フローを抽出し、変数依存関係を作成する。
- 2．
- 変数依存関係を元に、変数依存グラフを作成する。
- 3．
- 制御データの関係性を示す構造変化グラフを作成する。
- 4．
- 変数依存グラフと構造変化グラフを合成し、要因特定のためのグラフ（要因特定グラフ）を作成する。
以降、3.2節で変数依存関係を生成するためのプログラムスライシング技術、3.3節でPLC制御プログラムにおける変数依存グラフの生成方法、3.4節で構造変化グラフの生成方法、3.5節で要因特定グラフの生成方法を説明する。
3.2 プログラムスライシング
プログラムスライシングは、プログラムコードから変換された制御フローグラフに対して、制御依存解析とデータ依存解析を組み合わせることで、プログラム内の任意の文の変数に影響を与えるコードのみを抽出する技術7）である。
制御依存解析は、条件分岐などによって⽣じる「ある⽂の実⾏結果が、別の⽂が実⾏されるか否かを左右している」関係を抽出するもので、データ依存解析は、「ある⽂で定義されたデータがどの⽂で利⽤されているかを示す」関係図を得るための⼿法である。この2つの解析から、ある変数に注⽬した時、対応する頂点から依存関係を遡っていけば、その変数に関連する文のみを抽出し、影響する変数を特定することができる。
プログラムスライシングによる依存関係抽出には、着目する変数に影響を与える変数を抽出するための後ろ向きスライシングと、着目する変数が影響を与える変数を抽出するための前向きスライシングが存在する。
図4のサンプルプログラムから抽出した制御フローグラフにおいて、図5と図6に後ろ向きスライシングと前向きスライシングを適用した例を示す。
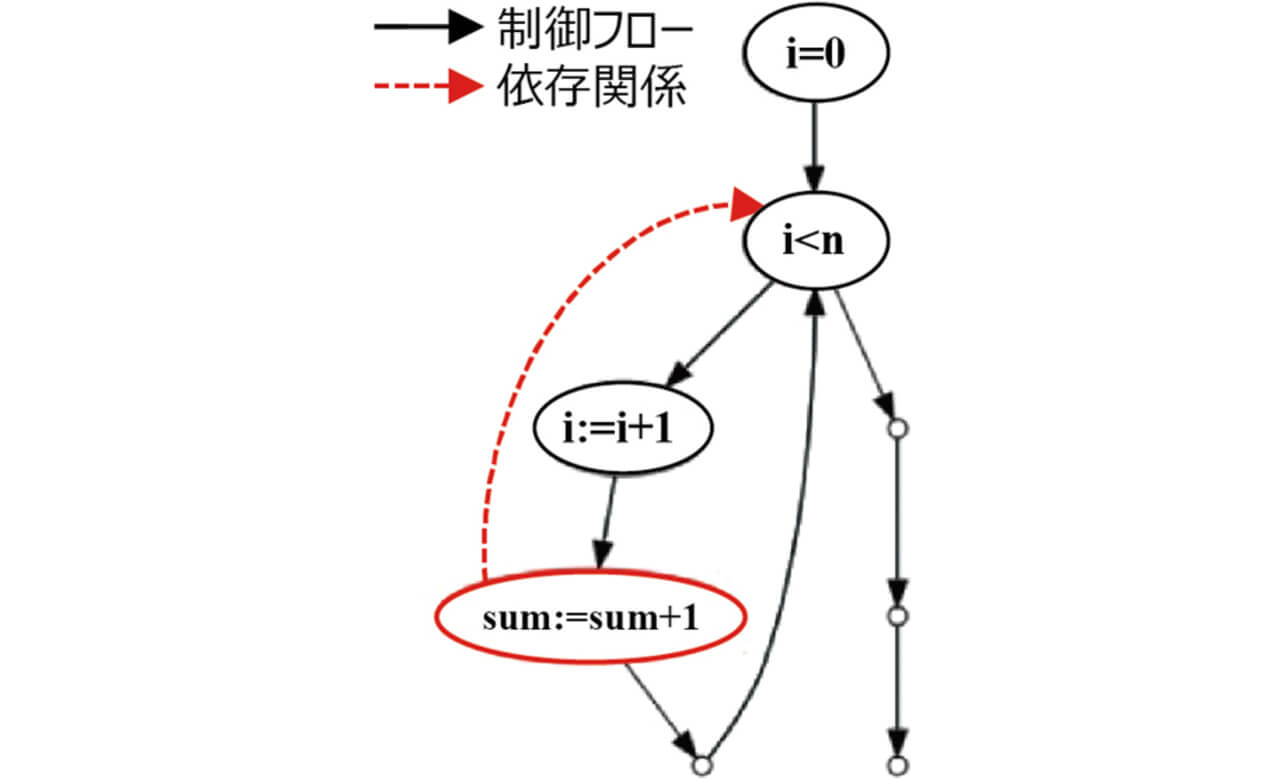
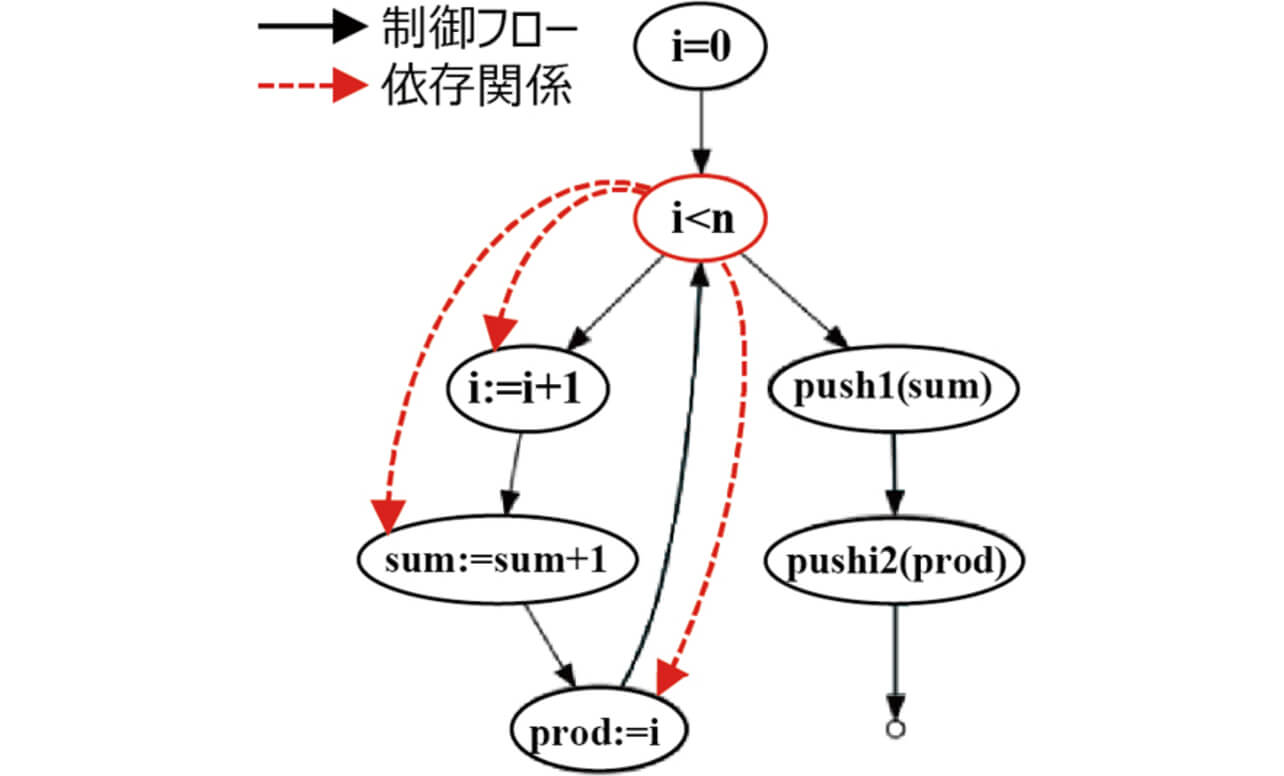
後ろ向きスライシングの結果、sumに影響を与える変数は n と i であり、前向きスライシングの結果、n が影響を与える変数は i 、sum、prodであることが分かる。変数の依存関係は、
のように表され、var1がvar2に影響を与えるときは1、影響を与えないときは0となる。
3.3 変数依存グラフ
本節では、プログラムスライシングをPLC制御プログラムに適用し、それぞれの変数依存関係から変数依存グラフを生成する手法を説明する。
本稿で扱うPLC制御プログラムは、PLCのプログラミング言語の国際規格であるIEC 61131-38）を対象とする。IEC 61131-3では、PROGRAM、内部状態の存在するFB（ファンクションブロック）、内部状態の存在しないFUN（ファンクション）の3種類の機能が定義されている。これらは工程や機能毎にプログラムを構造化し、プログラムの可読性向上や再利用を促進することを意図している。
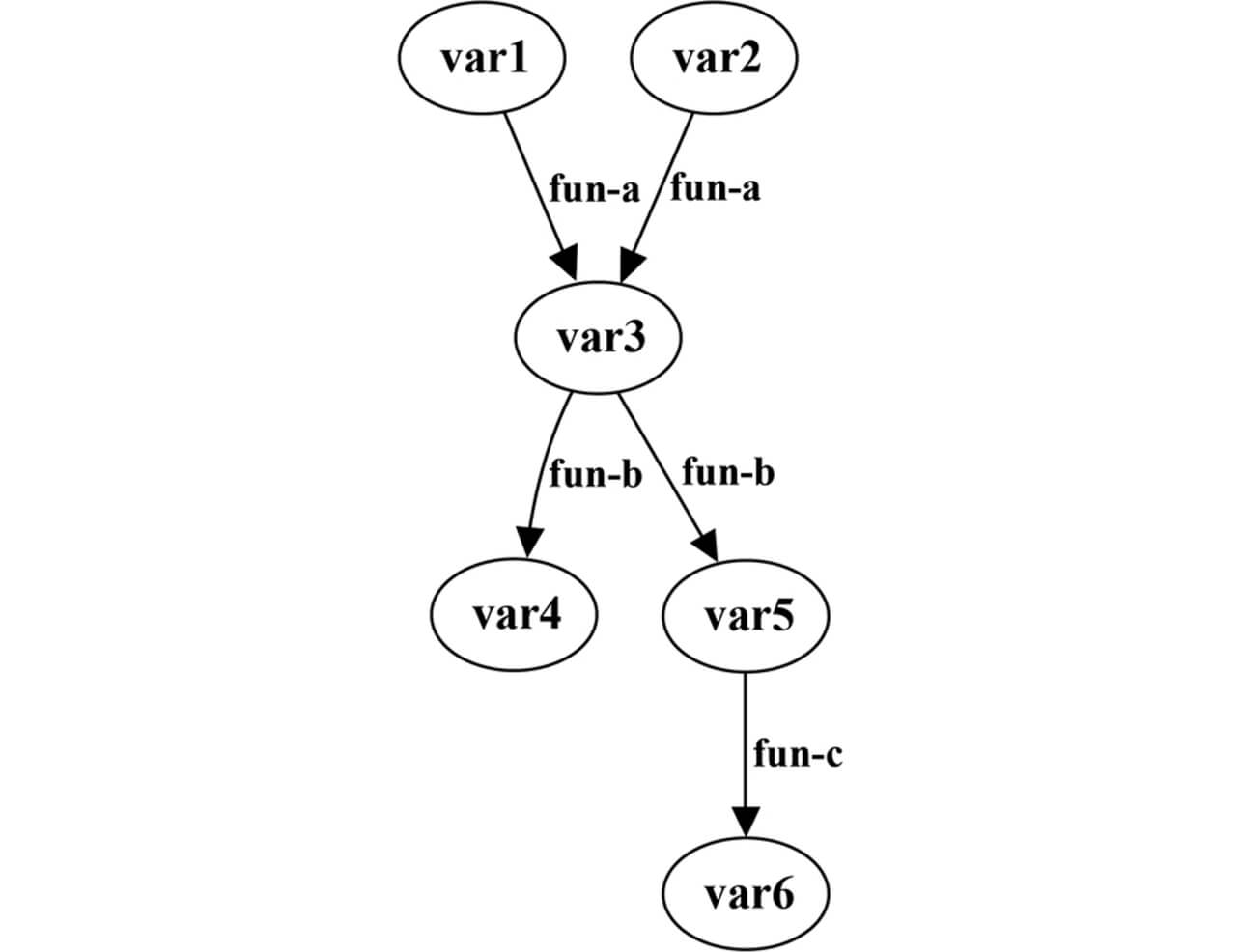
図7に、PLC制御プログラム振る舞いの例を示す。また、図7のプログラムについて、デバイスに割り付けられた変数（デバイス変数）の関係を表す変数依存グラフの例を図8に示す。
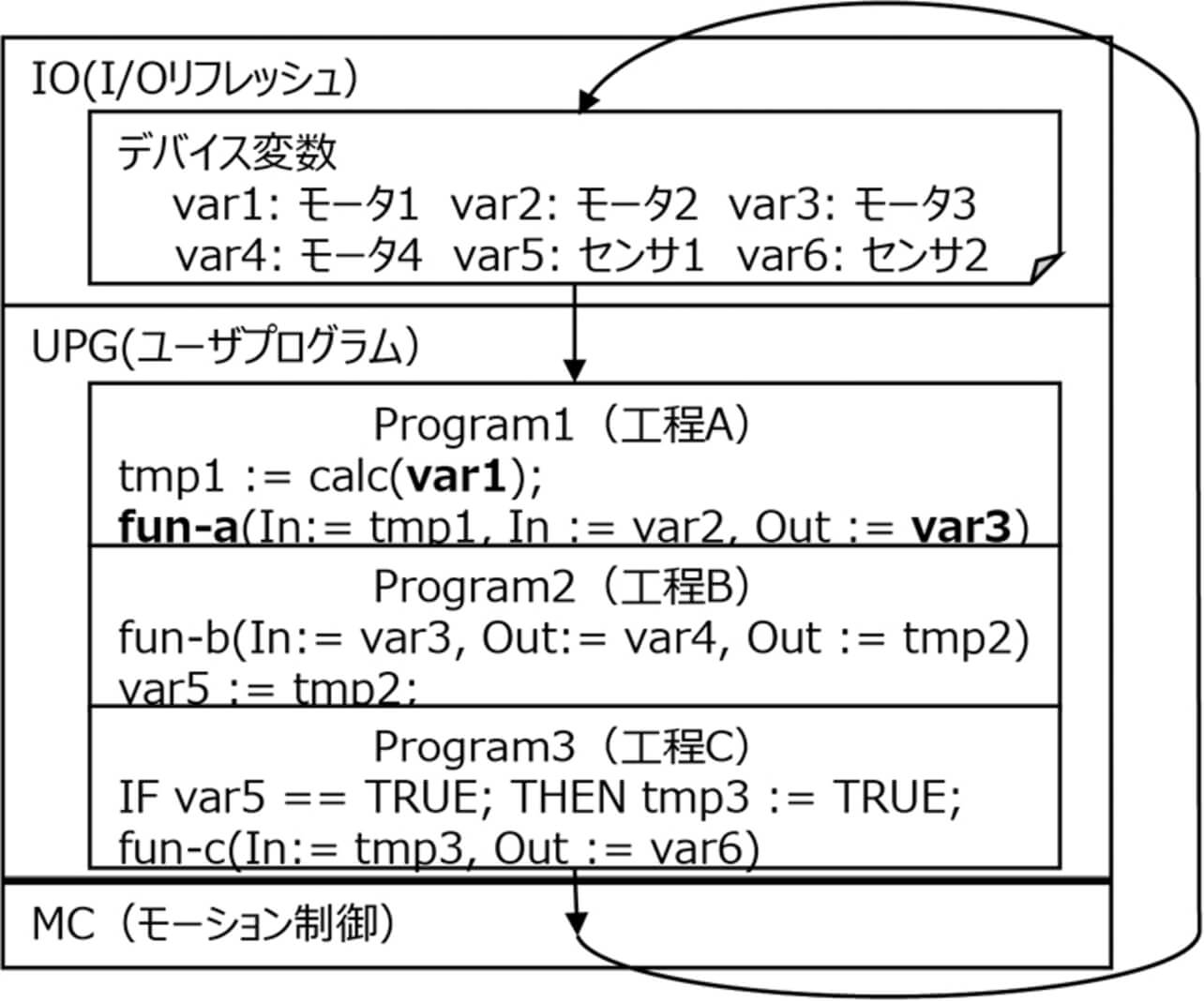
PLCは、I/O リフレッシュ（データ入出力）、ユーザプログラム実行（UPG）、モーション制御（MC）の処理を厳密な時間間隔で実行することで、高精度な制御を実現している。センサやモータなどのアクチュエータはデバイス変数としてI/O リフレッシュで更新される。ユーザプログラムは、それぞれの工程や機能に応じて、デバイス変数を入出力としてプログラムを実行する。
提案手法では、外部環境の変化を表しているデバイス変数に着目して、前向きスライシングを行うことで、変数間の依存関係を構築する。この依存関係に、各工程で具体的な処理を行うFBとFUNへの入出力情報を追加することにより、変数依存グラフを生成する。図7のProgram1において、変数var1が中間変数であるtmp1を介してfun-aに入力され、fun-aがvar3を出力することが、図8の変数依存グラフにも表されている。なお、fun-aにおいて、Inは入力変数、Outは出力変数を示す仮引数である。
図8に示すデバイス変数を 
として、変数依存グラフは、隣接行列を用いて式（2）で表される。
隣接行列は各変数を頂点とした正方行列として表現される。
は式（1）で示した変数間の依存関係となり、変数依存グラフは有向グラフとして表現される。
3.4 構造変化グラフ
変数依存グラフに合成することを目的とした制御データ関係性の表現は、単純な構造変化検知問題9）として、正常（良品）と異常（不良品）の相関行列の差で算出するアプローチが考えられる。一般的な相関行列で使用されるピアソンの積率相関係数は正規分布を仮定しているため、本稿では図2に示すような時系列の制御データ間の依存度表現に適した相互情報量を使用する。相互情報量は式（3）で表される。
は、製品1個を包装する区間で区切った制御データのペアである。相互情報量の算出方法としては、入力されたデータ空間をランダムなグリッドに区切り、相互情報量が最大となるグリッドを探索するMIC（Maximal Information Coefficient）10）を使用する。
すべての制御データ間で算出される相互情報量行列 
は式（4）で表される。
表2と表3に正常データと異常データそれぞれの相互情報量行列の例を示す。
| var1 | var2 | var3 | var4 | var5 | var6 | |
|---|---|---|---|---|---|---|
| var1 | 1.00 | 0.86 | 0.00 | 0.00 | 0.00 | 0.00 |
| var2 | 0.86 | 1.00 | 0.90 | 0.00 | 0.43 | 0.00 |
| var3 | 0.00 | 0.90 | 1.00 | 0.00 | 0.92 | 0.00 |
| var4 | 0.00 | 0.00 | 0.00 | 1.00 | 0.55 | 0.00 |
| var5 | 0.00 | 0.43 | 0.92 | 0.55 | 1.00 | 0.75 |
| var6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.75 | 1.00 |
| var1 | var2 | var3 | var4 | var5 | var6 | |
|---|---|---|---|---|---|---|
| var1 | 1.00 | 0.85 | 0.00 | 0.00 | 0.00 | 0.00 |
| var2 | 0.85 | 1.00 | 0.80 | 0.00 | 0.31 | 0.00 |
| var3 | 0.00 | 0.80 | 1.00 | 0.00 | 0.82 | 0.00 |
| var4 | 0.00 | 0.00 | 0.00 | 1.00 | 0.66 | 0.00 |
| var5 | 0.00 | 0.31 | 0.82 | 0.66 | 1.00 | 0.77 |
| var6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.77 | 1.00 |
次に、正常データと異常データの相互情報量の差分は式（5）により算出される。
ここで、
は正常データであり、
は異常データである。
最後に、構造変化グラフは式（6）から算出され、図9のように表される。
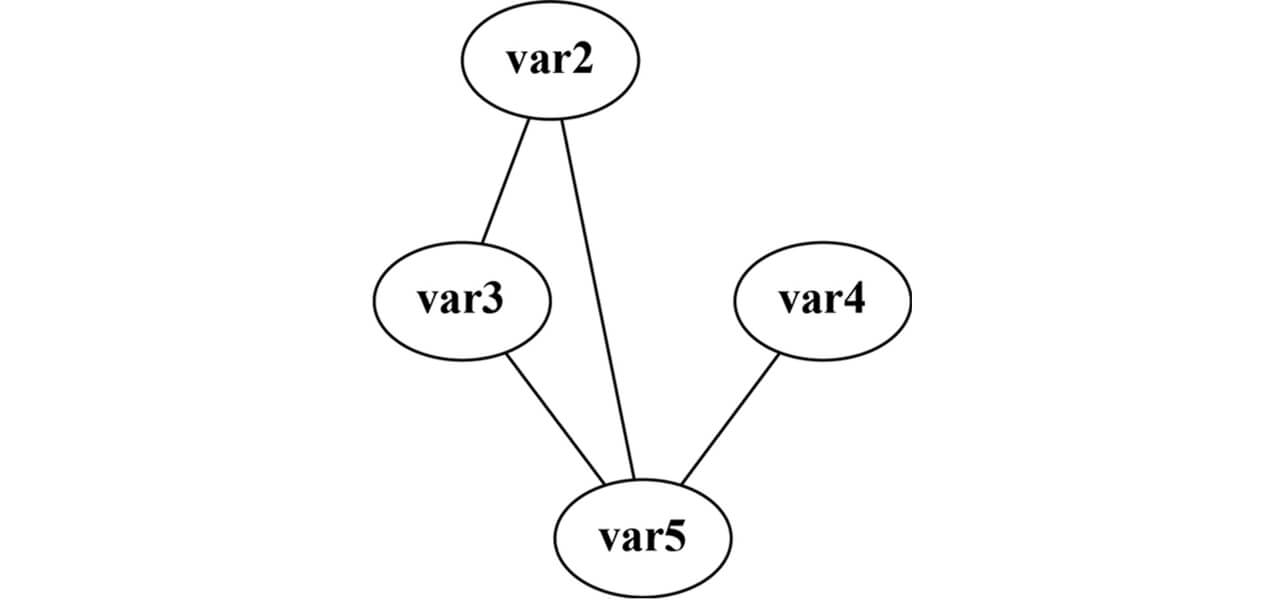
差分のしきい値を 
として、ステップ関数u で、しきい値を超える関係性のみを残すことにより、構造変化グラフが生成される。しきい値については、並べ替え検定で使用される5％水準と情報量の加法性から、相互情報量の差が0.05以上の場合に有意な差があるものとする11）。なお、構造変化グラフは無向グラフであるため、対称行列として表現される。
3.5 要因特定グラフ
要因特定グラフは式（7）から算出され、図10のように表される。
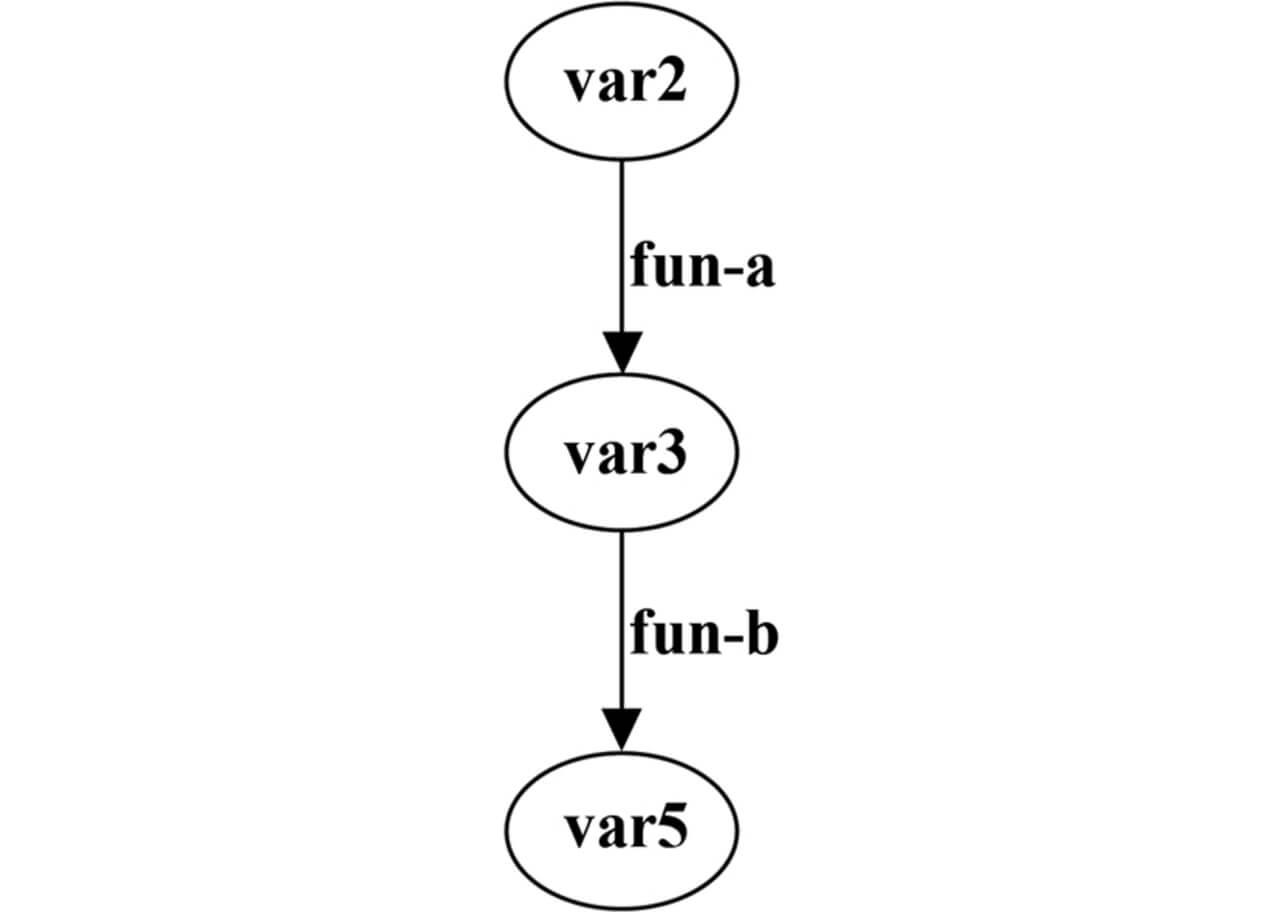
式（7）は行列成分毎の積であるアダマール積を用いている。
この例では、要因はvar2となり、fun-aを介してvar3に影響を与え、さらにvar3はfun-bを介してvar5に影響することを示している。構造変化グラフでは、var2とvar5およびvar4とvar5の関係性に変化が認められるが、変数依存グラフにおける関係は無いため、要因特定グラフとしては表現されないことになる。
4. 検証
本章では、2.1節で示した実験用包装機を用いて、提案手法の有効性について検証した結果を述べる。
4.1 検証内容
包装機で発生する代表的な不良は包装不良であるが、その要因は様々である。本稿では提案手法の有効性を検証するために、従来手法では要因を特定できない2種類の包装不良について検証した。表4に、今回実験した包装不良の概要を示す。
| 不良事象 | 概要 | 要因（該当する変数） |
|---|---|---|
| 包装不良1 | フィンガが変形したことにより、ワークの位置がずれて包装不良が発生する。 | ワーク位置ずれ （コンベア軸位置） |
| 包装不良2 | フィルム搬送軸のローラが平行でないため、フィルムが蛇行して包装不良が発生する。 | フィルム蛇行 （フィルム搬送軸1速度 フィルム搬送軸2速度） |
包装不良1については、ワークを送り出すフィンガが変形したことによりワークの位置ずれによる包装不良が発生する。包装不良2については、フィルムが蛇行することにより包装不良が発生する事象となっており、それぞれで要因が異なっている。次に、要因特定に使用する収集データについて、表5に示す。
| 対象 サーボモータ |
対象変数 | 制御データ（単位） |
|---|---|---|
| フィルム搬送軸1 | FilmFeedMain | FilmFeedMain.Trq（％） FilmFeedMain.Vel（mm/s） FilmFeedMain.Pos（mm） |
| フィルム搬送軸2 | FilmFeedSub | FilmFeedSub.Trq（％） FilmFeedSub.Vel（mm/s） FilmFeedSub.Pos（mm） |
| コンベア軸 | ProductFeed | ProductFeed.Trq（％） ProductFeed.Vel（mm/s） ProductFeed.Pos（mm） |
| トップシール軸 | TopSeal | TopSeal.Trq（％） TopSeal.Vel（mm/s） TopSeal.Pos（mm） |
| 仮想軸 | VirtualMaster | 無し |
この表では、包装機を構成するサーボモータに対して、制御プログラムの対象変数と収集される制御データに対応付けている。制御プログラムの対象変数には同期制御用の仮想軸を追加している。制御データは、PLCからの指令に追従してサーボモータを制御するサーボドライバのフィードバック値であるトルク（Trq）、速度（Pos）、位置（Vel）で構成される。なお、トルクは定格トルクを100％としたときの比率で表される。各制御データの単位は異なるが、3.4節で記した構造変化グラフを生成にはMICを使用しているため、正規化は不要となる。
4.2 検証結果
3.3節に示した手法で生成された変数依存グラフを図11に示す。
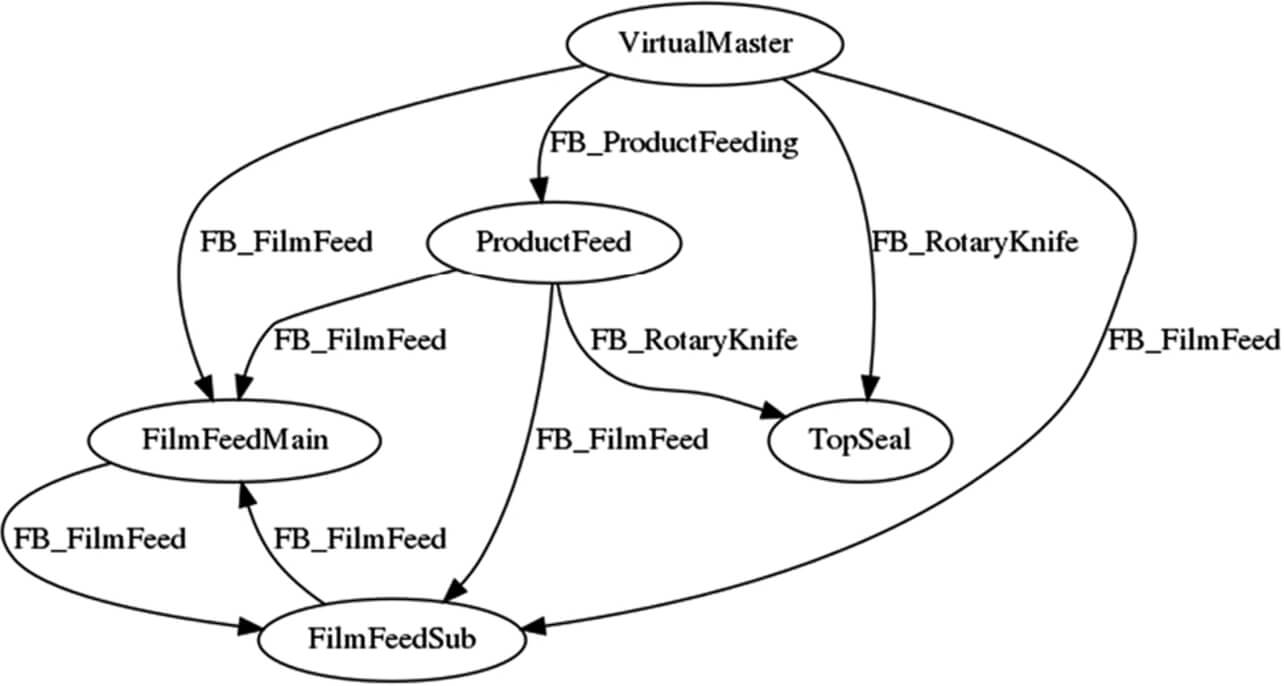
表6は、変数依存グラフから各工程で実行されるFB別に影響する変数を対応付けしたものである。
| 工程 | FB | 影響を与える変数 | 影響を受ける変数 |
|---|---|---|---|
| ワーク搬入工程 | FB_ProductFeeding | VirtualMaster（仮想軸） | ProductFeed（コンベア軸） |
| センターシール工程 | FB_FilmFeed | VirtualMaster（仮想軸） ProductFeed（コンベア軸） FilmFeedMain（フィルム搬送軸1） FilmFeedSub（フィルム搬送軸2） |
FilmFeedMain（フィルム搬送軸1） FilmFeedSub（フィルム搬送軸2） |
| エンドシール工程 | FB_RotaryKnife | VirtualMaster（仮想軸） ProductFeed（コンベア軸） |
TopSeal（トップシール軸） |
センターシール工程においては、フィルム搬送軸1と2が互いに影響して関係性が巡回していることが分かる。
次に、良品状態の制御データについて、3.4節によって算出された相互情報量行列を表7に示す。
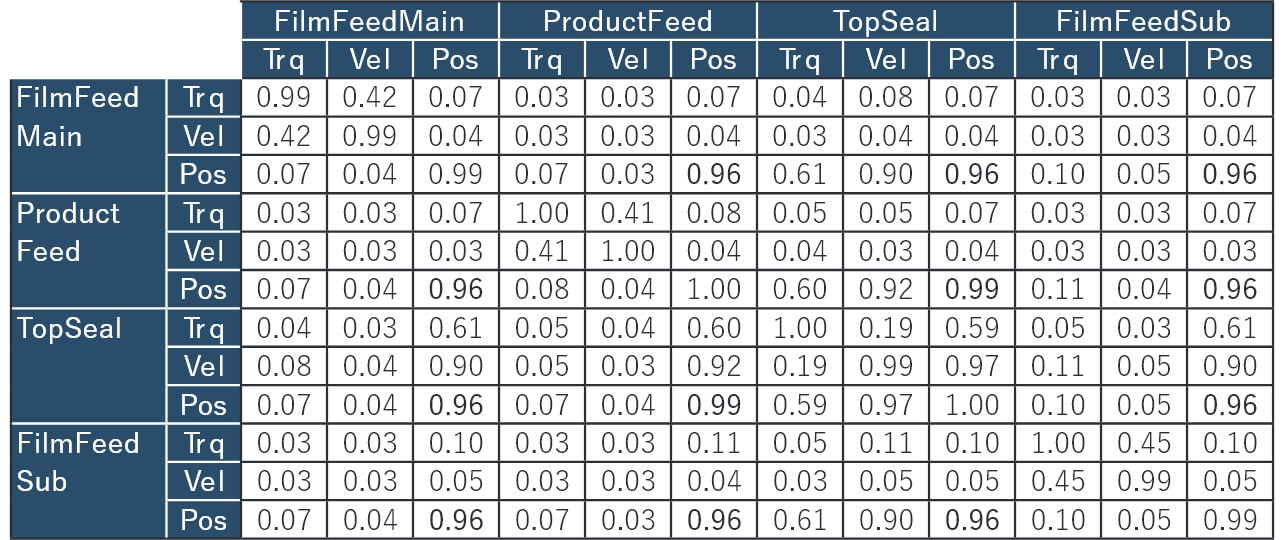
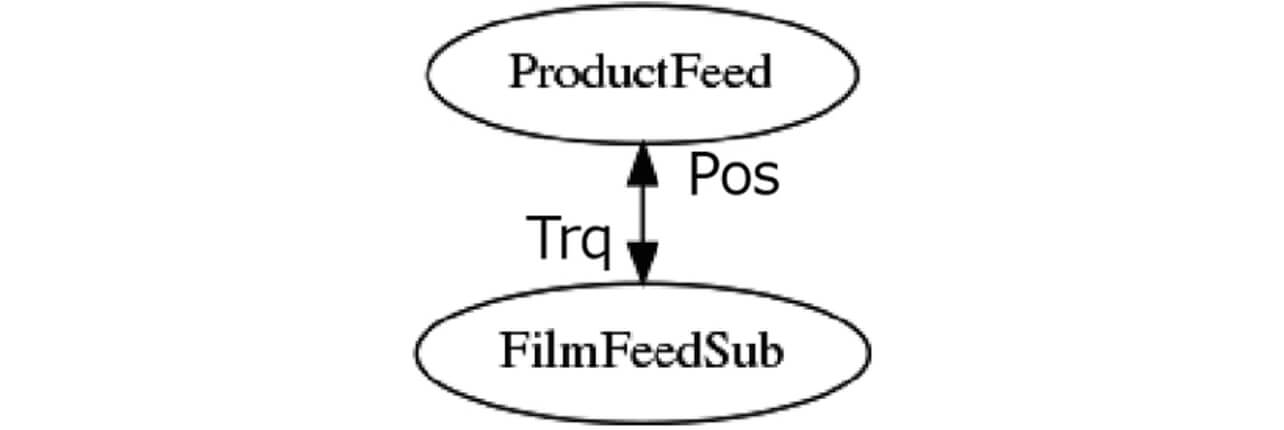
FilmFeedMain、ProductFeed、TopSeal、FilmFeedSubの全ての位置（Pos）が高い関係性（0.95以上）を示している。これは包装機がワーク搬送用ProductFeedから位置を同期制御しているためである。この結果から、FilmFeedMain、ProductFeed、TopSeal、FilmFeedSub全ての位置は、図11の変数依存グラフの上流であるProductFeedの位置に集約可能とする。
同様に、良品と包装不良1について、3.4節に示された手法で算出された相互情報量行列の差分を表8に示す。
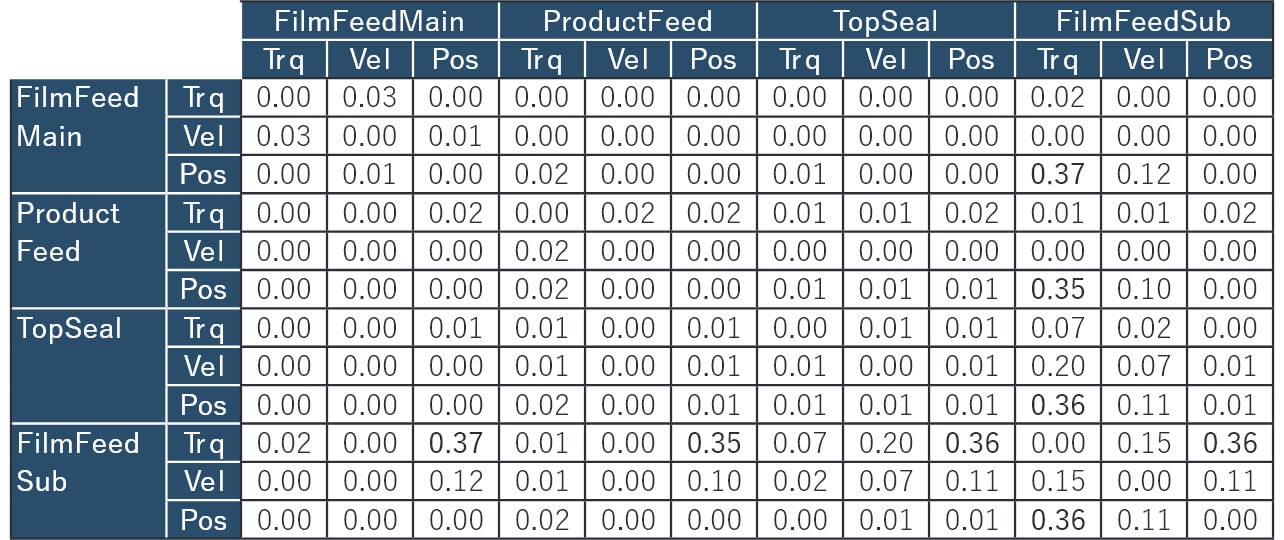
これらの結果から、しきい値を0.32として、構造変化グラフを生成したものを図12に示す。変数依存グラフと合成するために、トルクなどの要素はエッジ部に記載する表記としている。このグラフから、前述の通り位置情報をProductFeedに集約して表示したものを図13に示す。
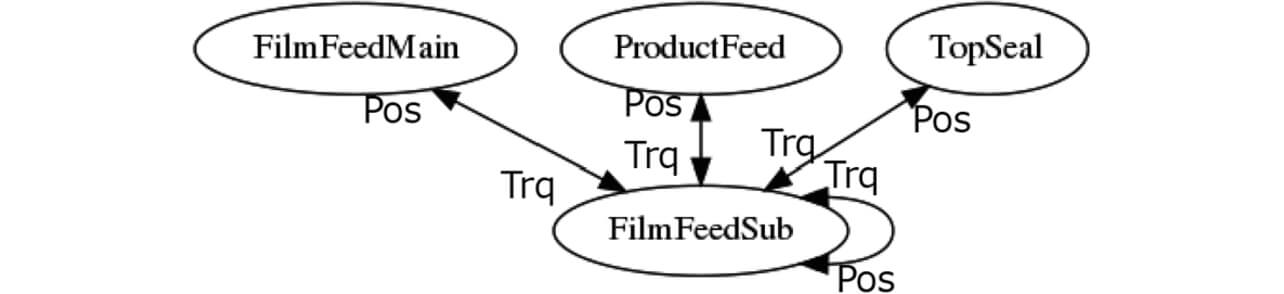
最後に、3.5節に示した手法で生成された要因特定グラフを図14に示す。
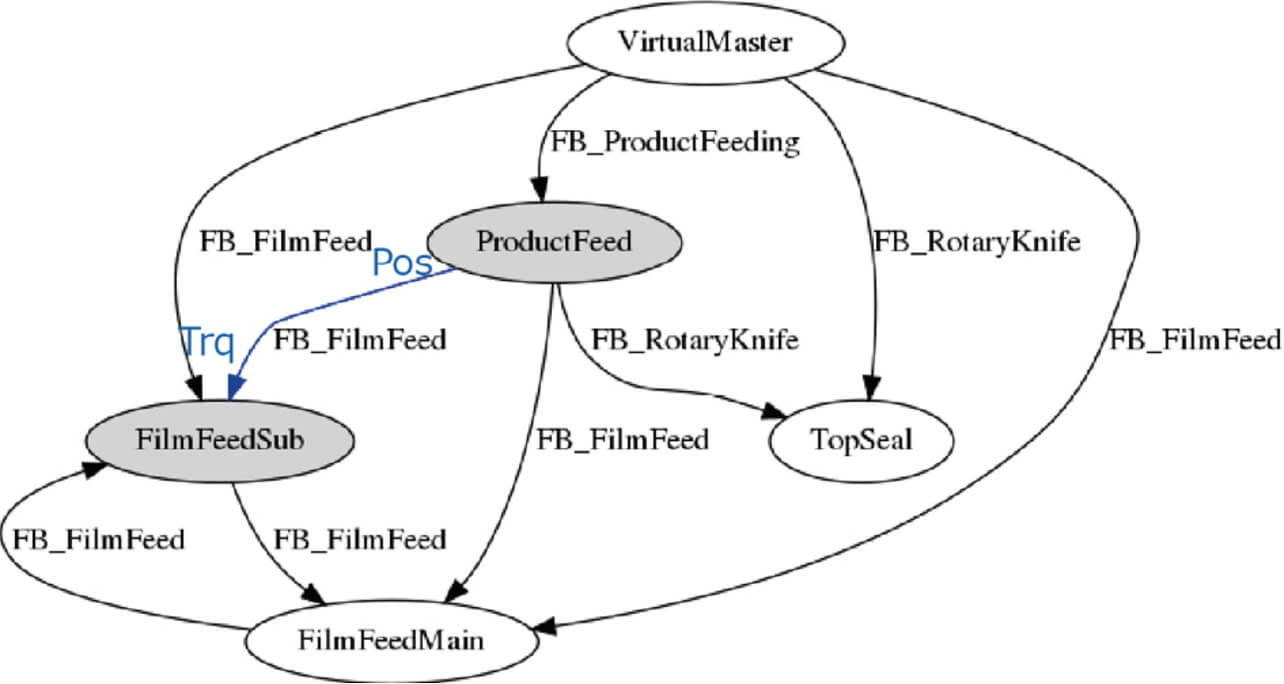
この結果、ワーク搬送工程を賄うProductFeedの位置情報が原因であるとし、要因であるコンベア軸位置と合致したことが分かる。
次に、同様の手法で生成された包装不良2に対する要因特定グラフを図15に示す。
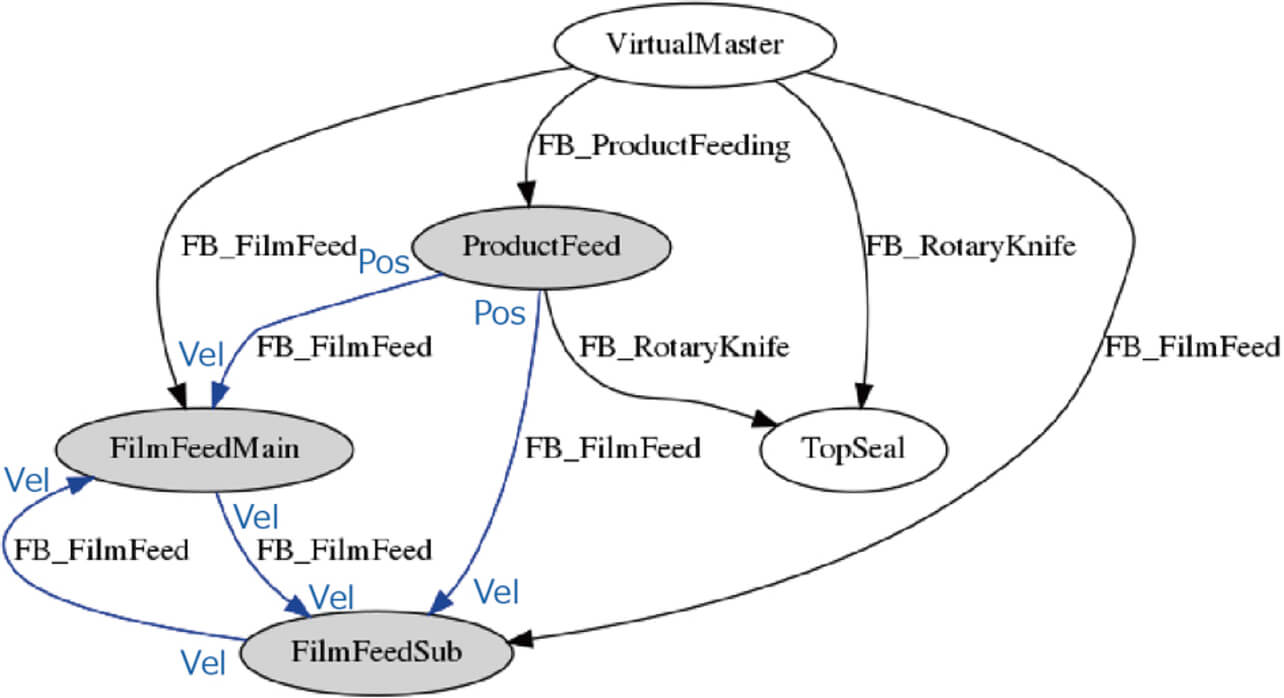
要因候補として、ProductFeedの位置がFilmFeedMain/Subの速度に影響を与えるものと、FilmFeedMain/Subの速度の関係性の崩れの2要因が想定される。
この不良要因は、フィルムの蛇行であり、フィルム搬送軸1と2であるFilmFeedMain/Subの速度関係性の崩れは要因と合致している。提案手法の要因特定結果について、表9にまとめる。
| 不良内容 | 要因 | 提案手法による特定要因結果 | 従来手法による要因特定結果 | 重要度 |
|---|---|---|---|---|
| 包装不良1 | ワーク位置ずれ （コンベア軸位置） |
コンベア軸位置 | フィルム搬送軸2トルク（標準偏差） フィルム搬送軸2速度（最大） トップシール軸トルク（最小） |
0.154 0.137 0.081 |
| コンベア軸位置（標準偏差） | 0.007 | |||
| 包装不良2 | フィルム蛇行 （フィルム搬送軸1速度 フィルム搬送軸2速度） |
コンベア軸位置 フィルム搬送軸1、2の速度の関係崩れ |
フィルム搬送軸1 トルク（平均） トップシール軸トルク（最小） トップシール軸速度（最小） |
0.169 0.123 0.120 |
| フィルム搬送軸1 速度（平均） フィルム搬送軸2 速度（平均） |
0.016 0.031 |
これは、表4に示した不良内容と要因に、提案手法と従来手法による要因特定結果を追記したものである。
提案手法では、包装不良1については目論見通りの要因を特定し、包装不良2については要因候補を2つまで絞り込むことが出来た。従来手法では、2.3節と同様にRandomForestの重要度により算出された上位3つの特徴量と、本来の要因に該当する特徴量の重要度を記載している。従来手法で特定された特徴量の重要度は、本来の要因の特徴量の重要度と比較して高い値となっており、要因特定としては適切ではないことが分かる。
4.3 考察
本節では、変数依存グラフ、構造変化グラフを構成するための相互情報量行列、要因特定それぞれの妥当性について考察する。
変数依存グラフに関しては、目論見通り工程の情報を抽出して変数の関係性を表現することが出来た。良品のみの相互情報量行列については、サーボモータの位置同期制御が明確に表現されており、制御観点から納得性の高い結果が得られたと考える。
包装不良1については、ワーク搬入工程であるコンベア軸の位置情報を要因として、正しく特定することが出来た。包装不良2については、コンベア軸の位置情報とフィルム搬送軸1、2の速度関係性という要因特定候補を2種類まで絞り込むことが出来た。従来手法では後工程の要因が特定される傾向にあるが、提案手法では本来の要因を特定しており、要因特定としては有効であると考える。
なお、包装不良2について、1種類まで要因特定出来ずにコンベア軸の位置が選択された原因としては、データの関係性に着目しているため、エッジの片方のみに変化があると、もう片方も抽出されてしまうことが考えられる。今後はデータ関係性に特徴量重要度を加えるなどの改善を検討する必要がある。
また、本稿では、4つのサーボモータから構成される比較的小規模なシステムを対象としたが、製造ラインのスコープでは100程度のサーボモータから構成される大規模なシステムも対象として考えられる。提案手法では、大規模システムにおいても要因特定グラフの生成は可能ではあるものの、サーボモータ数が20程度を超える場合には要因特定グラフが複雑になり、解釈性に課題があるため、今後の検討事項とする。
5. むすび
本稿では、FA領域の製造現場で不良要因を特定する目的において、複数工程が同期する独立性が低いデータ課題に対して、プログラムスライシング技術を適用し、複数工程処理と同期制御の情報を持つPLC制御プログラムから知識情報を抽出してデータ解析に統合する手法を提案した。さらに、実験用包装機を対象とした有効性検証により、従来手法では特定できなかった要因についても有効性を示すことが出来た。さらに、提案手法はPLC制御プログラムからの知識情報を抽出するため、実プログラムを確認せずに実施可能となり、要因解析工数の削減にもつながる。
今後の展望としては、データの関係性の精度改善と大規模なシステムへの適用に加えて、対象とする制御プログラムを他社製PLCに適応させることや、設計資料などプログラム以外の情報から知識情報を抽出することにより、適用範囲を拡大させていきたい。
参考文献
- 1）
- 株式会社東芝．“要因解析技術 HMLasso”．東芝AI技術カタログ．2020-04-01．https://www.global.toshiba/jp/technology/corporate/ai/catalog013.html，（参照 2022-03-01）．
- 2）
- 日本電気株式会社．“要因分析エンジンを用いた工場・プラントでの品質管理”．NEC技報．2016-09．https://jpn.nec.com/techrep/journal/g16/n01/160114.html，（参照 2022-03-01）．
- 3）
- 石川馨．品質管理入門．第3版，日科技連出版社，1989.
- 4）
- 鶴田浩輔，峯本俊文，広橋佑紀．マシンコントローラに搭載可能なAI技術の開発（1）．OMRON TECHNICS. 2018, Vol.50, No.1, p.6-11.
- 5）
- 宮本 幸太，川ノ上 真輔．AI搭載マシンオートメーションコントローラの開発（3） ．OMRON TECHNICS. 2019, Vol.51, No.1, p.52-57.
- 6）
- Productivity Press Development Team. OEE for Operators: Overall Equipment Effectiveness. 1st ed., Productivity Press. 2018.
- 7）
- Binkley, D. W.; Gallagher, K. B. Program slicing. Advances in Computers. 1996, Vol.43, p.1-50.
- 8）
- オムロン株式会社．“PLCの国際標準プログラミング：IEC 61131-3とは？”．Sysmac統合プラットフォーム．https://www.fa.omron.co.jp/product/special/sysmac/plcopen/feature1.html，（参照 2022-03-01）．
- 9）
- 井手剛，杉山将．異常検知と変化検知．講談社，2015, p.162.
- 10）
- Reshef, D. N. et al. Detecting Novel Associations in Large Data Sets. Science. 2011, Vol.334, No.6062, p.1518-1524.
- 11）
- 杉山将，入江清，友納正裕．相互情報量を用いた機械学習とそのロボティクスへの応用．日本ロボット学会誌．2015, Vol.33, No.2, p.86-91.
本文に掲載の商品の名称は、各社が商標としている場合があります。