新しい現場で簡単に立ち上げる
ある環境におけるタスクに関して獲得された知識を活用し、別の環境におけるタスクの学習を効率化するアプローチとして転移学習がある。本稿では特に転移強化学習をとりあげ、その概要を紹介するとともに、著者らの最近の成果であるMULTIPOLAR(MULTI-source POLicy AggRegation)を解説する。
MULTIPOLARは、転移元・転移先環境の間で状態遷移確率分布が未知かつ異なる状況を対象とした転移強化学習手法である。同様の問題を扱う先行研究の多くと異なり、MULIPOLARは転移元環境において獲得された方策関数を適応的に統合して学習に利用するため、環境において学習サンプルを収集する必要がないという利点がある。OpenAI Gym環境におけるシミュレーション評価によって、MULTIPOLARの有効性を確認している。
1. まえがき
機械学習においてモデルが識別や生成、制御といったタスクを実現できるようにするためには、そのタスクにおいて期待される入出力を表現するデータ(学習データ)を収集する必要がある。このデータ収集が機械学習を成功させる鍵の一つとなる―ある現場において、モデルに高いパフォーマンスを発揮させるためには、その環境に現れうる現象を広くカバーした学習データを用意できていることが望ましい。なぜならば、学習されたモデルを同現場において運用する際、学習時に含まれなかった入力に対して期待される出力を得ることは必ずしも保証されないためである。
一方で、現実世界において機械学習モデルの運用を期待する現場は数多く存在するものの、また現場によってデータの計測条件やタスクの細かな種別はしばしば異なる。「監視カメラの設置場所ごとに光源環境が異なる」「製造現場においてラインごとに扱う部品が異なる」などがその例である。これに対して、現場ごとにデータを大量に収集・学習することで、その現場に適応した高パフォーマンスのモデルが獲得できると考えられる。しかしながら、データ収集・学習それぞれにかかる時間・資源的コストの観点から、このようなアプローチは必ずしも現実的ではない。
このような課題を解決する一つのアプローチとして、転移学習と呼ばれる技術がある。転移学習は「ある問題(転移先)を効果的かつ効率的に解くために、別の関連した問題(転移元)のデータや学習結果を再利用する」技術を広く指す1)(括弧内は著者による注記)。「ある問題」を「新しい現場におけるモデルの運用」、「別の関連した問題のデータ」を「そのモデルを学習するために別の現場で収集したデータ」と読み替えると、先の課題との対応が見える。すなわち転移学習を用いることで、多様な現場のそれぞれにおいて機械学習モデルを一から構築するのではなく、過去の現場から得られた何らかのデータを活用して学習を効率的にすることができる。より具体的には、たとえば扱う部品が同種ではあるが完全には一致しないような製造ラインが多数存在するとき、あるラインで収集したデータや獲得したモデルを用いて、別のラインにおける機械学習モデルの立ち上げを早期化・省力化することが期待される。
このような転移学習は、機械学習およびその関連分野において長らく取り組まれてきた課題である。深層学習の発展とともに近年研究が活発であるドメイン適応やマルチタスク学習、メタ学習などのトピックとも関連が深い。さらに、転移元・転移先においてどのようなデータが利用可能かによって、様々な派生問題やその解決手段が存在する。本稿では、転移強化学習―すなわち強化学習のための転移学習を取り上げ、その概要に加えて「転移元と転移先で環境の従う状態遷移確率分布が異なる」「転移元における生データにアクセスできない」といった状況を扱うことが可能な著者らの研究成果2)を紹介する。
2. 研究の背景
2.1 強化学習
転移強化学習の前に、まずは基本的な強化学習3)の問題設定と応用について簡単に述べる。強化学習では、マルコフ決定過程(Markov Decision Process; MDP)でモデル化された環境において、ある決められたルール(方策;policy)に基づいて行動するエージェントを考える(図1)。MDPはM =(
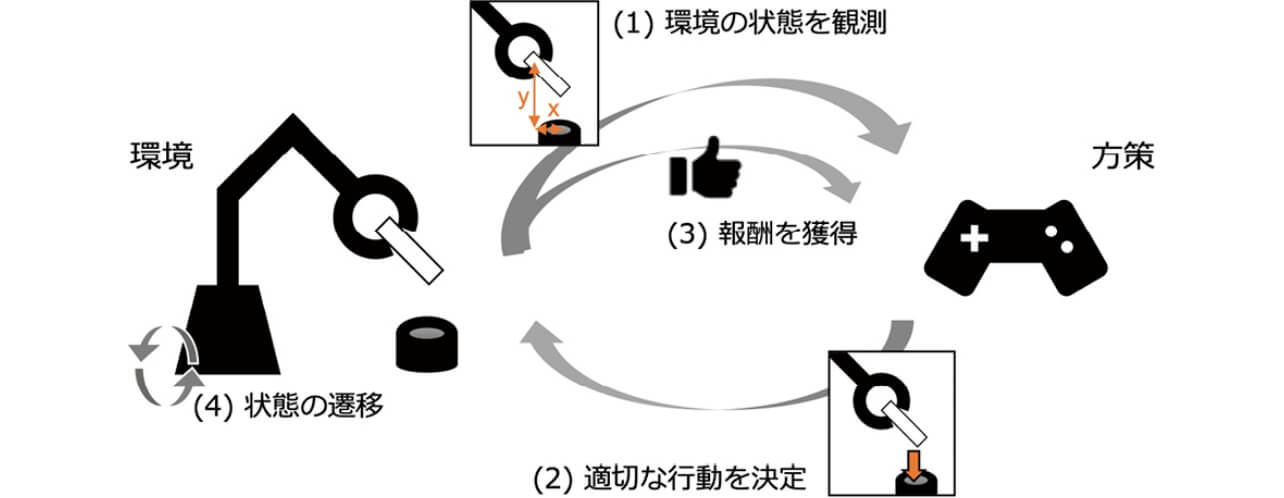
このように強化学習は、エージェントによる個別の行動に対して何かしらの明確な正解が与えられるのではなく、行動の“良さ”を示す報酬という量のみが教師信号として与えられる点、そのようななかで単一時刻における適切な行動ではなく、長期にわたる行動の“系列”を推定する必要がある点などにおいて、一般によく知られる教師あり学習とは大きく異なる。その結果、強化学習はロボットマニピュレータの制御や自動走行ロボットの制御4)、ヘルスケア5)、ゲームAI6)など、「ある環境において、長期的に効果のある意思決定をしたい」という要求のある応用シーンにおいて、幅広い活用が期待されている。
一方で、強化学習では固定された学習データセットが与えられるのではなく、エージェント自身の行動に基づいて学習サンプルが逐次的に収集されることになる。そのため、エージェントの行動に対して何かしらのリスク(たとえば誤ったマニピュレーションによってロボットが緊急停止、あるいは破損してしまうなど)が無視できないケースでは、「いかに少ないデータから良い方策を学習できるか」が重要な課題となる。これを解決する一つのアプローチが、次節で紹介する転移強化学習である。
2.2 転移強化学習
転移強化学習では、転移元の環境で得られた知識を活用することにより、転移先における強化学習をなるべく少ないサンプルで実現することを目指す7)。それぞれの環境はMDPによってモデル化され、転移元・転移先のMDPがどのように異なるか、転移元環境の“知識”として具体的に何が与えられるかといった条件に基づいて、いくつかの問題に派生する。たとえば、Successor Featuresと呼ばれる有名な研究8)では、転移元と転移先で報酬関数が異なる状況を扱っている。転移元からは状態遷移サンプル(st , at , st +1)が収集され、そのサンプルを用いて新たな環境における未知の報酬関数を推定するという形で方策の学習を効率化する。より挑戦的な課題として状態空間、行動空間、および状態遷移確率分布までもが環境間で異なるという状況を扱う研究も存在する9)。同研究はこのようなケースに対して、両環境で共通に利用できる特徴空間を学習し、そこで方策を学習することによる転移を実現している。
2.3 状態遷移確率分布の異なる環境間の転移
とりわけ本稿では、環境間で状態遷移確率分布T のみが異なるという問題設定を考える。直感的には、「エージェントが同一の状態st で同一の行動at を取った後の、次の状態st +1(より正確には次にある特定の状態に遷移する確率)が異なる」ということを示す。たとえば、ロボットマニピュレータにおいてリンクの長さや重さが異なるケースが挙げられる10)。また、自動走行ロボットの制御においては、車載物の重量や路面状況が状態遷移確率分布に影響を与えるであろう。文献10)で取り上げられているように、このような課題の難しさは、実際の状態遷移確率分布が転移元・転移先それぞれの環境においてしばしば未知であるという点にある。したがって、未知の状態遷移確率分布をどのように推定するか、あるいは環境間の状態遷移確率分布の違いをどのように定量化するかが、同問題を扱う転移強化学習において重要な課題となる。
このような課題に取り組んだ関連文献を紹介したい。転移強化学習における先述の課題を解決するために、既存研究の多くは転移元の環境から学習サンプル(st,at,st+1 )あるいは(st,at,st+1,rt )を大量に収集し活用する。たとえば文献11)12)では、転移元から収集したサンプルを利用して転移元・転移先におけるMDPの違いを定量化している。このような定量化に基づいて、転移先に最も類似する転移元環境を特定し、転移学習に活用することができる。一方、文献10)では転移元環境が多数与えられる問題設定を取り上げ、環境を表現する条件パラメタ(explicit encodingやimplicit encodingと呼ばれる)に応じて異なる行動を出力可能な方策を学習する。これにより、未知の転移先環境においても、その環境に対応する条件パラメタから適切な行動を選択可能となっている。同文献ではさらに環境間で状態空間や行動空間が異なる状況においても同様の手法が適用できる可能性を示している。
なお、多数の転移元環境を想定した設定は、メタ学習やマルチタスク学習等類似するトピックの研究でも見られる。たとえば文献13)では、それぞれ異なるルールに従うサブ方策と、与えられたタスクに対してどのサブ方策を利用するかを決定するマスター方策を、多様な環境から収集されたサンプルを用いてメタ学習するアプローチを提案している。類似するアプローチはActor-mimicと呼ばれる手法14)でも採用されており、ルールの異なるゲームを複数用いた方策のマルチタスク学習にもとづいて、新たなゲームにおいても効率的に方策を転移できることを示している。
3. MULTIPOLAR: Multi-source Policy Aggregation
以降では、環境間で状態遷移確率分布の異なる状況を想定した転移強化学習に関する、著者らの近年の取り組み2)を紹介する。まず本節では研究のモチベーションと具体的なアプローチを解説し、次節で評価実験の結果を報告する。
3.1 モチベーション
2.3節で紹介したとおり、環境間における状態遷移確率分布の違いを扱う既存研究は、しばしば転移元における学習サンプルが大量に必要となる。しかしながら、このような前提に基づく学習は現実の場面において必ずしも容易ではない。たとえば、さまざまな製造現場においてロボットがマニピュレーションタスクに取り組むシナリオを考える。たとえそれらのタスクが同一であったとしても、ロボットの持つキネマティクスやダイナミクスが異なれば、それらは異なったMDPとしてモデル化されることとなり、結果として最適となる方策も異なる10)。各環境においてサンプルを大量に収集し学習に活用できるかどうかは、現場それぞれのストレージや通信環境に依存する。たとえばセキュリティ等の都合から閉じたネットワークの中でロボットが稼働するケースであれば、転移元環境から逐次的に学習サンプルを集める必要のある既存手法10)13)14)の適用は難しい。
これに対して本研究では、(複数の)転移元環境から何らかの方法で獲得された方策関数が与えられるという別の問題設定を考える。製造現場における上記の例であれば、各現場において個別のロボットを動かす制御アルゴリズム(=方策関数)を集約し活用することで、新たな現場における方策の獲得を効率化することを目指す。このような方策関数は、ヒューリスティックに設計されたルールの集合であろうと、強化学習を含む機械学習でデータドリブンに獲得されたモデルであろうと、既存研究で必要とされる学習サンプル集合と比較するとデータサイズが大幅に小さく、また転移元・転移先間での情報のやりとりも一度ですむため、先に述べたストレージや通信環境に関する課題に対処することができる。一方で、各転移元環境から共有された方策関数自体は同環境の状態遷移を記述するものではない。すなわち、転移先環境においてその方策がどの程度有効に働くかは未知という新たな問題が生まれることになる。
これに対して本研究では、MULTIPOLAR(MULTI-source POLicy AggRegation)と呼ばれる新たな転移強化学習手法により、この問題の解決を目指す。MULTIPOLARは、複数の転移元環境から収集された方策関数の出力を、転移先環境における累積報酬が最大化されるように、強化学習の枠組みの中で“適応的に統合”する。以降の節で解説するように、この統合は転移元・転移先環境それぞれの状態遷移確率分布が未知であっても実現できる。さらに、同じく方策の統合を行う他の手法15)と異なり、行動空間が連続・離散いずれの場合も扱うことができるという応用範囲の広さを利点として持つ。
3.2 準備
MULTIPOLARの解説にあたって、与えられた複数の転移元各環境をインデクス付きのMDP Mi =(
このような状況において本研究では、ある環境Mi において方策関数 μi : S →A が与えられるものとする。この方策関数μi は決定的であり、ニューラルネットワークのように陽にパラメタ化されたモデル、あるいは人によってヒューリスティックに設計されたアルゴリズムなど、さまざまな形態をとりうる。いずれにしても、それぞれの方策関数がどのような状態遷移確率分布を持つ環境でどのように設計・獲得されており、転移先環境においてどの程度の性能を発揮するかは、学習時に未知である。
いま、合計K 種類の転移元環境から方策関数の集合L = {μ1 ,…, μK }が与えられたとする。このとき、本研究のゴールは、新たな環境において累積報酬を最大化する方策 πtarget(at | st; L,θ )のパラメタθ を、強化学習のなかで効率的に推定することとなる。
3.3 方策関数の適応的統合
以下では、MULTIPOLARの一番のポイントである方策関数の統合について述べる(図2も参照)。転移先環境において観測された状態st に対して、ある転移元の方策関数μi を用いて決定的に得られる行動を 


![At=[(at(1))T,...,(at(K))T]∈RK×D](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-002-fig-01.svg)
MULTIPOLAR では、このAt を強化学習のループにおいて累積報酬を最大化させるように適応的に統合する。この統合結果は転移先での方策の学習において「およそこのように行動すれば良い」という帰納バイアスを与えるものであり、転移元の状態遷移分布Ti を知ることなく推定可能である。より具体的には、以下のような適応的統合関数Fagg: S →A を定義する。

ただし、

3.4 補助ネットワーク
図2に示すように、MULTIPOLARではFagg に加え、以下のような補助ネットワークFaux: S →A を導入する。
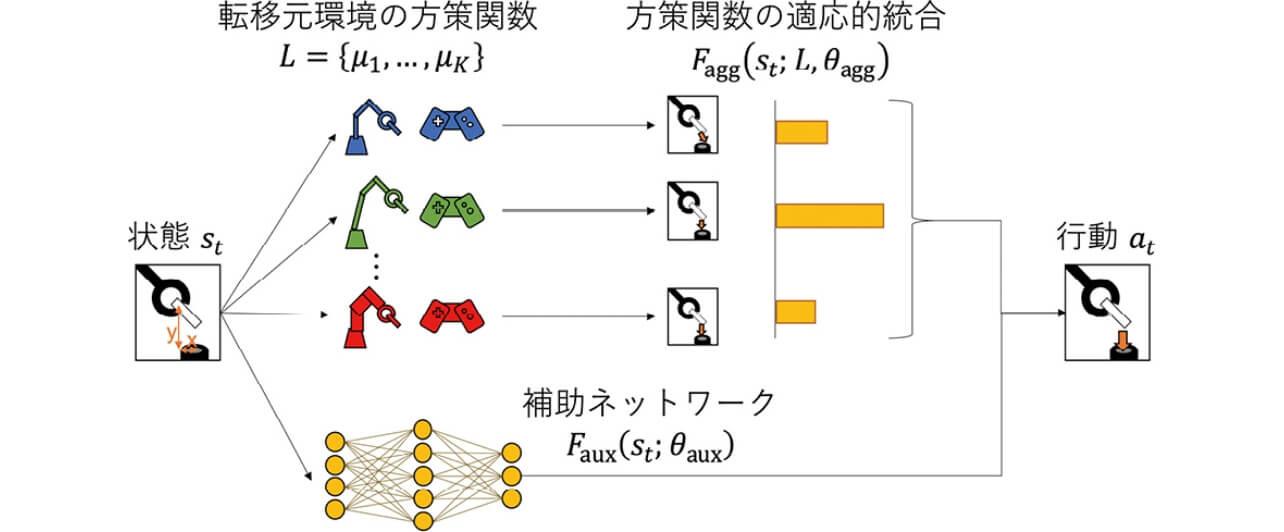

この補助ネットワークFauxは2種類の機能を持つ。
- 1)
- もしFaggが転移先環境において既に最適に近い行動を出力できている場合、Fauxはさらに高い累積報酬を獲得するための「補正項」としての役割を果たす。
- 2)
- 一方でFaggが転移先環境において有効でない場合、Fauxは累積報酬を最大化するための行動を学習することができる。なお、類似したアプローチは残差方策学習(residual policy learning)と呼ばれる手法16)17)にも見られる。ただしこれらの既存研究は、転移元の方策が単一、かつ行動空間が連続という状況のみを扱うという点で本研究の取り組みとは大きく異なる。
3.5 方策の構成
上記の関数F(st; L,θagg,θaux)をリパラメタライズすることで、転移先環境の方策 πtarget(at | st; L,θ )として用いることができる。たとえば連続行動空間を扱う場合、F(st; L,θagg ,θaux )を平均とするガウシアン方策としてπtargetを与えればよい。一方、行動空間が離散である場合、F(st; L,θagg,θaux)をソフトマックス関数によって正規化することで方策として扱うことができる。いずれの場合も、方策πtarget(at | st; L,θ )のパラメタはθ = [θagg,θaux]のみであり、方策を直接更新可能な標準的な強化学習アルゴリズムによって学習可能である。
4. MULTIPOLARの性能評価
本節では、文献2)において実施したOpenAI GymによるMULTIPOLARの評価結果を紹介する。なお、本評価実験に用いたプログラムは、著者らのGitHubリポジトリ(https://github.com/omron-sinicx/multipolar)において公開されている。
4.1 評価設定
評価環境として、OpenAI GymからCartPole, Acrobot, LunarLander, RoboschoolHopper, Roboschool Ant, Roboschool InvertedPendulumSwingUpという6種類のシミュレーション環境を選択した。それぞれの環境は、ロボットのリンク長や重量、摩擦など、MDPの状態遷移確率分布を特徴づけるいくつかのキネマティクス、ダイナミクスパラメタが含まれる。本評価ではこのパラメタをランダムに変化させることにより、環境ごとに状態遷移分布の異なる100種類の環境インスタンスを作成した。いくつかの例を図3に示す。
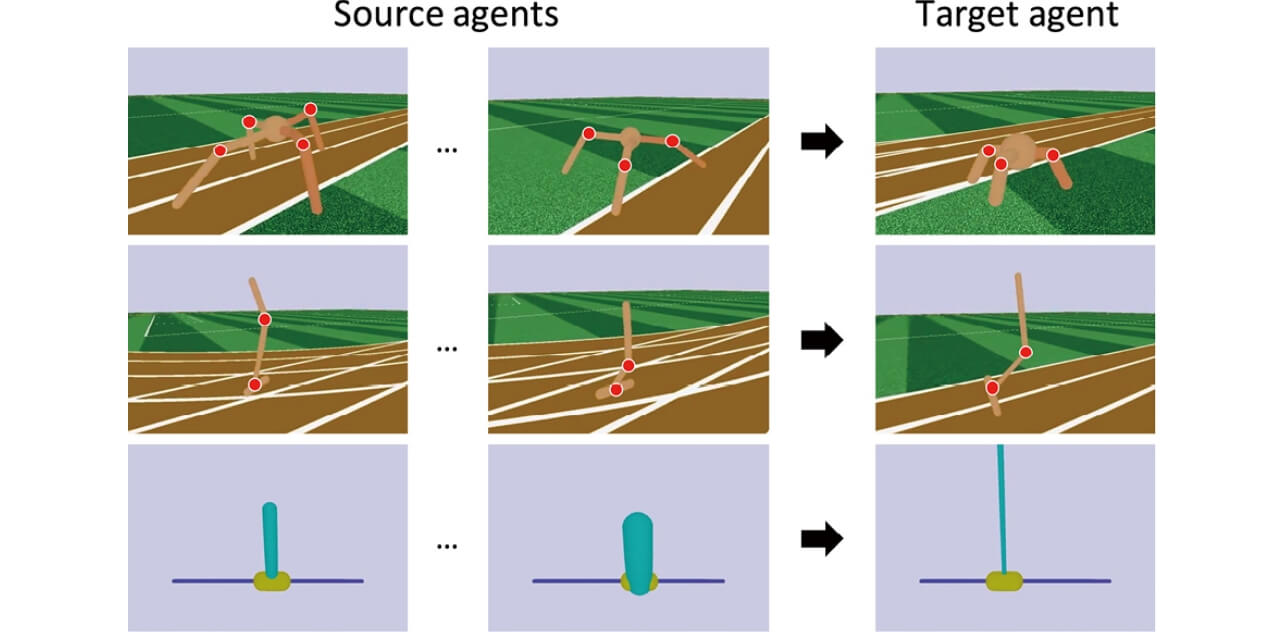
さらに、各環境インスタンスに対して、多層パーセプトロン(MLP)でモデル化された方策を学習し、転移元における方策関数として利用した。MULTIPOLARの評価にあたっては、1)まず100種類のうちそれぞれのインスタンスを転移先環境として設定し、2)自身以外でランダムに選択されたK=4種類のインスタンスを転移元環境としてさらに選択、対応する方策関数の集合L = {μ1, ..., μK }を利用することで、3)転移先環境におけるエピソード報酬(episodic reward)がタイムステップとともにどのように改善されていくかを記録、他手法と比較した。
4.2 実装と比較手法
全ての実験はStable Baselines18)をベースとした実装により実施した。LunarLander環境ではSoft Actor Critic19)、その他の環境ではProximal Policy Optimization20)を用いて方策を学習した。
またMULTIPOLARの比較手法として、以下を評価した。
- 多層パーセプトロン(MLP):転移先環境で新規に方策を学習するベースラインであり、転移元環境の情報の有無が与える影響を評価できる。
- 残差方策学習(Residual policy learning; RPL):MULTIPOLARにおいてK =1の場合に相当するベースラインであり、転移元環境が複数与えられることの利点を評価できる。
- Attend, adapt, and transfer (A2T)15):MULTIPOLARにおいてFaggのパラメタが、st を入力とした別モデルによって与えらえる場合に対応する。もともとA2Tは離散行動空間のみを扱うが、ここではMULTIPOLARと同様に統合結果をガウシアン方策の平均として利用することで、連続行動空間における学習に対応した。
4.3 実験結果
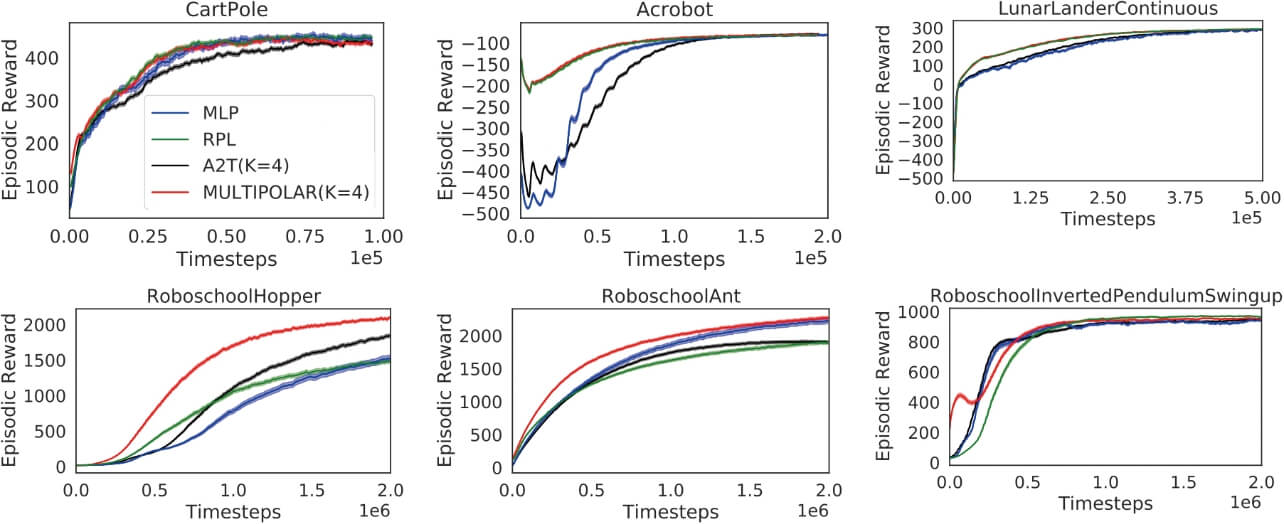
図4に環境・手法ごとのエピソード報酬の変化をプロットした。さらに、学習終了時における、全エピソードにわたるエピソード報酬の平均値(average episodic reward)を表1に示した。
| CartPole | Acrobot | LunarLander | |
|---|---|---|---|
| MLP | 291 | -111 | 216 |
| RPL | 289 | -98 | 246 |
| A2T | 281 | -120 | 226 |
| MULTIPOLAR | 299 | -96 | 246 |
| Hopper | Ant | InvertPendulum | |
| MLP | 92 | 1500 | 409 |
| RPL | 152 | 1432 | 322 |
| A2T | 126 | 1361 | 458 |
| MULTIPOLAR | 283 | 1744 | 588 |
CartPoleのような簡単な環境を除いて、転移元環境の方策を活用するRPL, A2T, MULTIPOLARはより少ないタイムステップで高いエピソード報酬を獲得できていることが分かる。これらの3手法間の優劣は環境によって異なるが、いずれの場合もMULTIPOLARが最も高い性能を示している。
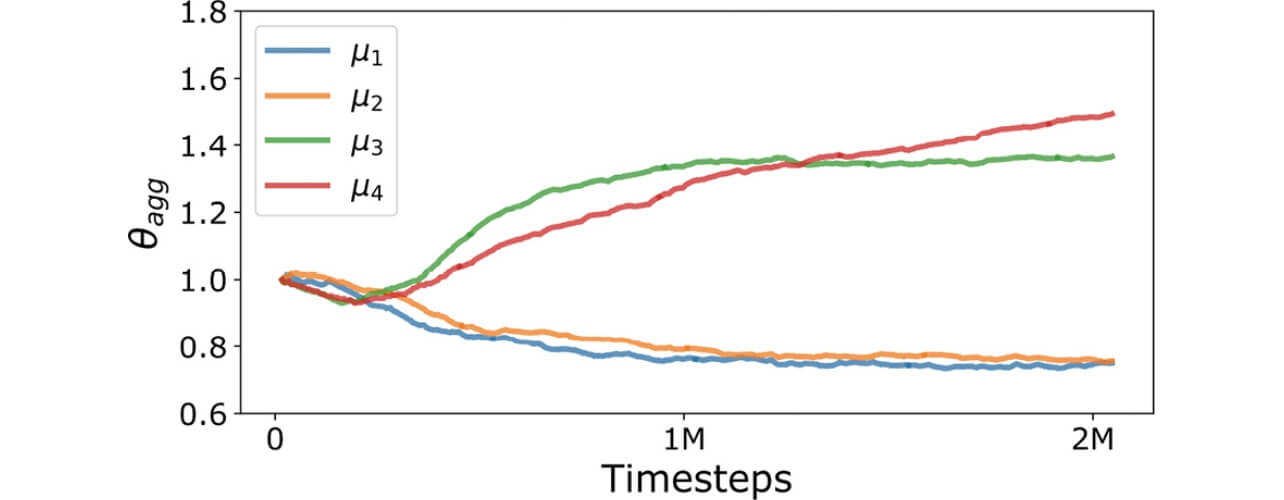
MULTIPOLARの挙動をさらに分析するため、図5では4種類の方策関数のうち2種類を高性能な方策(μ1,μ2)、残り2種類を低性能な方策(μ3,μ4)とした際の重みθaggを示した。タイムステップの増加にともない、高性能な方策関数により大きな重みが与えられるように学習が進んでいることが分かる。
5. むすび
本稿では、既存の環境で得られた知識を活用して新たな環境における強化学習を効率化するアプローチとして転移強化学習をとりあげ、その概要を解説した。また、環境間で状態遷移確率分布が未知かつ異なる状況に適した転移強化学習手法として、MULTIPOLARについて紹介した。MULTIPOLARは転移元環境で獲得された方策関数を活用するため、同環境において学習サンプルを大量に集める必要がない。また、行動空間が連続・離散いずれの場合においても、一貫した方法によって方策の転移を実現できる。
MULTIPOLARは、強化学習の中でも特にモデルフリー学習を対象とした手法である。一方、転移元で獲得されたモデルを転移先環境において適応的に統合するというアプローチ自体は汎用的であり、我々はモデルベース強化学習21)、教師あり学習22)、教師なし学習23)においてもその有効性を確認している。興味のある読者は参照されたい。
参考文献
- 1)
- 神蔦敏弘.転移学習.人工知能学会誌.2010, Vol.25, No.4, p.572-580.
- 2)
- Barekatain, M. et al. “MULTIPOLAR: Multi-Source Policy Aggregation for Transfer Reinforcement Learning between Diverse Environmental Dynamics”. Proceedings of the International Joint Conference on Artificial Intelligence. 2020, p.3108-3116. doi:10.24963/ijcai.2020/430.
- 3)
- Sutton, R. S.; Barto, A. G. Introduction to Reinforcement Learning. 1st ed., MIT Press, 1998.
- 4)
- Kober, J. et al. Reinforcement Learning in Robotics: A Survey. The International Journal of Robotics Research. 2013, Vol.32, No.11, p.1238-1274.
- 5)
- Gottesman, O. et al. Guidelines for Reinforcement Learning in Healthcare. Nature Medicine. 2019, Vol.25, No.1, p.16-18.
- 6)
- Mnih, V. et al. Human-Level Control through Deep Reinforcement Learning. Nature. 2015, Vol.518, No.7540, p.529-533.
- 7)
- Taylor, M. E.; Stone, P. Transfer Learning for Reinforcement Learning Domains: A Survey. Journal of Machine Learning Research. 2009, Vol.10, No.7, p.1633-1685.
- 8)
- Barreto, A. et al. “Successor Features for Transfer in Reinforcement Learning”. Proceedings of the Annual Conference on Neural Information Processing Systems. 2017, p.4058-4068.
- 9)
- Gupta, A. et al. “Learning Invariant Feature Spaces to Transfer Skills with Reinforcement Learning”. Proceedings of International Conference on Learning Representations. 2017, p.1-14.
- 10)
- Chen, T. et al. “Hardware Conditioned Policies for Multi-Robot Transfer Learning”. Proceedings of Annual Conference on Neural Information Processing Systems. 2018, p.9355-9366.
- 11)
- Ammar, H. B. et al. “An Automated Measure of MDP Similarity for Transfer in Reinforcement Learning”. Workshops at the AAAI Conference on Artificial Intelligence. 2014, p.31-37.
- 12)
- Song, J. et al. “Measuring the Distance between Finite Markov Decision Processes”. Proceedings of International Conference on Autonomous Agents & Multiagent Systems. 2016, p.468-476.
- 13)
- Frans, K. et al. “Meta Learning Shared Hierarchies”. Proceedings of International Conference on Learning Representations. 2018.
- 14)
- Parisotto, E. et al. “Actor-Mimic: Deep Multitask and Transfer Reinforcement Learning”. Proceedings of International Conference on Learning Representations. 2016, p.1-16.
- 15)
- Rajendran, J. et al. “Attend, Adapt and Transfer: Attentive Deep Architecture for Adaptive Transfer from Multiple Sources in the Same Domain”. Proceedings of International Conference on Learning Representations. 2017, p.1-18.
- 16)
- Silver, T. et al. Residual Policy Learning. arXiv preprint arXiv:1812.06298. 2018.
- 17)
- Johannink, T. et al. “Residual Reinforcement Learning for Robot Control”. Proceedings of International Conference on Robotics and Automation. 2019, p.6023-6029.
- 18)
- Hill, A. et al. Stable Baselines. https://github.com/hill-a/stable-baselines. 2018.
- 19)
- Haarnoja, T. et al. “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor”. Proceedings of International Conference on Machine Learning. 2018, Vol.80, p.1861-1870.
- 20)
- Schulman, J. et al. Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347. 2017.
- 21)
- Tanaka, K. et al. “TRANS-AM: Transfer Learning by Aggregating Dynamics Models for Soft Robotic Assembly”. Proceedings of International Conference on Robotics and Automation. 2021, https://ieeexplore.ieee.org/xpl/conhome/1000639/all-proceedings, to appear.
- 22)
- Ma, J. et al. “Adaptive Distillation for Decentralized Learning from Heterogeneous Clients”. Proceedings of International Conference on Pattern Recognition. 2020, p.7486-7492.
- 23)
- Yonetani, R. et al. Decentralized Learning of Generative Adversarial Networks from Non-iid Data. arXiv preprint arXiv:1905.09684. 2019.
本文に掲載の商品の名称は、各社が商標としている場合があります。














