ILO(Input-Logic-Output)摺り合わせ制御技術
- ILO摺り合わせ制御技術
- マシンオートメーションコントローラ
- モデル予測制御(MPC)
- ビジュアルフィードバック制御
- 制御理論
ものづくりの生産工程における様々な制御課題の解決に向けて、オムロンはILO(Input-Logic-Output)の高度な摺り合わせ制御技術を追求している。具体的には、高速高精度の計測と制御が可能なILO機器に加えて、制御理論の適用とILO機器の協調動作による制御アプリケーションのライブラリを提供している。
本稿では、制御理論適用の事例として、モデル予測制御(MPC)による高精度指令追従性能を実現する位置制御方式の概要と効果例を報告する。XYステージによる円形の連続軌跡制御で、同一軌跡精度の実現に対して、従来制御方式の約4倍の動作速度が可能になった。制御対象モデルを自動作成する機能を備えており、簡単に使用できる特長も備える。また、ILO機器の協調動作事例として、ビジュアルフィードバック制御による高速アライメントの概要と効果例を報告する。本方式はワークを止めずに画像センサによる位置計測を繰り返しながら対象物の位置合わせを行うアライメント方式であり、ワークが停止してから撮像を行う従来方式に比べて、目標精度±1 µmのアライメント時間を約1/4に短縮できた。アライメント時間の短縮効果に加えて、画像系と機械系の座標変換のキャリブレーションパラメータのずれに対するロバスト性が高いという特長も備える。
1. まえがき
近年のものづくりは、スマートフォンに代表されるデジタル製品、電動化が進む自動車を中心として進化が速く、制御技術への期待が大きくなっている。本稿ではものづくりの内、設計工程を除き、製造工程における制御課題を対象にする。製造工程は加工、組み立て、搬送、検査などで構成される。
デジタル製品では、構成部品である半導体や各種電子部品の微細化が進み、加工、組み立て、検査のすべてにおいて、生産性を維持しながら高精度化が求められている。また、部品の微細化に伴い、部品にダメージを与えないように、組み立て時の接触荷重を微小な値に抑制する要求が増えている。高精度化も微小な接触荷重も、加工組み立ての速度を下げることで対応できることがあり、その場合はタクトタイムとのトレードオフを如何に高いレベルで解決するかという課題になる。
従来、最先端の要求は装置メーカが独自に開発する制御システムで対応されてきたが、産業用汎用コントローラの性能・機能両面の能力向上に伴い、PLC(Programmable Logic Controller)あるいはモーションコントローラの採用が検討される機会が増えている。この期待に応えるべく、センシング機器(Input)、コントローラ(Logic)、ドライブ機器(Output)の高度な摺り合わせに基づく制御技術について報告する。
2. ものづくりにおける制御課題
ものづくりの製造工程における制御課題は、製造品目と製造工程の組み合わせ毎に様々であるが、精度、生産性、コストに分類すると表1のようになる。制御量により精度の表現は複数あるが、指令値あるいは目標値との偏差を小さくすることが基本である。これら3者間にはトレードオフの関係があり、いかに高いレベルで両立できるかが重要である。例えば軌跡制御では動作速度を下げれば軌跡精度の向上は可能であるが、それでは課題解決にはならない。通常は製造物によって目標精度は決まっているので、精度を確保できる範囲で動作速度をどこまで上げられるかを追求することになる。しかし、高額な計測制御機器を必要としたり、多大なチューニング工数が必要になるのでは、現実的な解決策にならないこともある。
| 制御量 | 精度 | 生産性 | コスト |
|---|---|---|---|
| 位置、距離 | 位置決め精度、軌跡精度、アライメント精度、振動抑制、多軸同期精度、オーバーシュート抑制 | 動作速度向上 整定時間短縮 |
調整工数低減 コスト低減 |
| 速度 | 安定性、多軸同期精度 | ||
| 荷重、テンション、温度 | 安定性、オーバーシュート抑制、多点均一性 |
そして、制御課題を解決するためには、表2に示すような制御課題解決を難しくする要因を克服しなければならない。これがILO摺り合わせ制御技術の役割である。
| 制御対象起因 | 外乱(非定型、定型)、機械の低剛性、特性変化(機差、経年変化)、負荷変動、ワーク公差、非線形特性(摩擦、デッドゾーン、ヒステリシス含む)、むだ時間、干渉 |
|---|---|
| 制御システム起因 | 計測性能不足(応答性、分解能)、演算性能不足(制御周期)、ILO間非同期による入出力応答時間ばらつき、ILO間キャリブレーション誤差、通信時間や制御周期によるむだ時間 |
3. ILO(Input-Logic-Output)摺り合わせ制御技術
オムロンは、画像センサFHおよび変位センサZW(Input)、マシンオートメーションコントローラNJ/NX/NY(Logic)、サーボドライバ1S/G5(Output)、などの高速高精度を追求する計測制御機器を揃えており、高精度同期を可能とするフィールドネットワークEtherCAT®での接続により、最速125 µs/8軸、軸間同期精度1 µsの制御システムを構築できる。さらに、多軸モーションコントローラPMAC(Logic)では、入出力機器をアナログ信号で接続することにより、最速16.6 µs/1軸、50 µs/8軸の超高速制御周期が可能となる。
しかし、ILO機器の高速高精度化は、表2の制御システム起因の要因の軽減には効くが、多くの場合で制御対象起因の要因には効かない。例えば応答遅れが大きい制御対象の位置制御で指令追従性を向上したい場合に、コントローラやサーボドライバの制御周期を高速化しても効果はない。また、軸間で応答遅れの差が大きい場合には、各軸の出力で同期精度を高めても、その先の機械動作における同期精度まで十分に向上できる保証はない。機械の特性を改善するのが最良の方法だが、制御の対応としては、機械の特性を考慮した適切な制御理論の適用が重要になる。PLCなどの汎用コントローラに搭載されている制御理論はPID制御に留まっていることが多い。その理由は、制御対象を特定できないため高度制御に必要な制御対象特性のモデル化が難しいことと、制御理論毎に異なる制御パラメータの調整が難しいことだと考えられる 1)。特定装置向けの専用コントローラでは、機械の特性を完全に把握できるため、制御対象モデルに基づく高度な制御理論の適用が進んでいる 2) 3)。なお、装置メーカがPLCを使用して、ユーザプログラムで高度な制御理論を搭載することは珍しいことではない。
また、ILO各機器には制約があり、それをILOの協調により上手く回避することが重要になる。例えば、変位センサにおける計測精度と計測範囲はトレードオフの関係があるが、ここにならい制御を適用し、変位センサとワークの距離が計測範囲に収まるように、変位センサを移動させることにより、高精度計測の計測範囲を拡大できる。
これまでに開発を進めてきた主な制御技術と効果例を表3に示す。
| 制御技術 | 効果例 |
|---|---|
| 制振制御 | 搬送速度向上、液面振動と傾き抑制 |
| 学習制御 | 軌跡精度向上、位置決め時間短縮 |
| モデル予測制御(MPC) | 軌跡精度向上、位置決め時間短縮 |
| スライディングモード制御 | 負荷変動に対する高ロバスト性 |
| インピーダンス制御 | 接触荷重のオーバーシュート抑制 |
| 外力推定 | ウェブの低テンション搬送 |
| ビジュアルフィードバック制御 | アライメント時間短縮、キャリブレーション誤差に対する高ロバスト性 |
| スペクトル分解制御 | 応答速度が異なるアクチュエータの協調動作による加工精度・速度向上 |
| 予測同期制御 | 多軸の同期精度向上 |
| ならい制御 | 変位計を用いる高精度2次元形状計測 |
本稿では、制御理論適用の事例としてモデル予測制御(MPC: Model Predictive Control)による高精度指令追従性能を実現する位置制御方式の概要と効果例を報告する。また、ILO機器の協調動作事例として、ビジュアルフィードバック制御による高速アライメントの概要と効果例を報告する。
4. MPCの位置制御への適用
4.1 MPCの概要
制御技術を起点に加工のタクトタイム短縮に貢献する方法としては、指令値への追従性向上、振動の抑制、外乱影響の低減などが考えられるが、装置や工程によって必要性や重要度が異なる。本稿では、その中で最も基本的な性能である指令値への追従性向上に効果する、MPCの位置制御への適用について報告する。MPCはプロセス制御領域での適用実績は豊富であり普及している4)が、モーション制御領域での適用事例の報告はまだ多くない。その理由の一つは計算負荷の高さであるが、複数の方式があるMPCの中には今回採用するPFC(Predictive Functional Control)5) 6) のように計算負荷が低い方式もあり、プレス装置の力制御への適用事例 7) が報告されている。別の理由として、MPCにおける予測が特に有効なのは、制御対象の特性に大きなむだ時間や遅れが含まれる場合であるが、モーション制御においてはむだ時間や遅れが小さいために、この点での期待が小さかったものと考える。しかし、ILO間が通信で接続される構成では、機械の応答遅れに通信遅れ(むだ時間)が加わり、さらに指令追従性能の要求が高くなると、指令値を生成するコントローラからみた指令値に対するフィードバック値の追従遅れが問題になる。そこで、指令追従性能の向上を狙い、MPCをモーション制御領域の位置制御に適用した。良好な制御性能が得られるサーボ系の制御方式として、PID制御をベースとするモデル追従型2自由度制御 8) が知られるが、むだ時間を明示的に考慮できる点と、未来の指令値を使用できる点を重視してMPCを採用した。
MPCは制御対象のモデルを使用して、予測ホライズンと呼ぶ有限区間の制御状態が最適になるように、将来の操作量パターンを決定し、最初の制御周期分の操作量だけを実際に出力するという処理を繰り返す。
図1にPFCにおける操作量計算の概念図を示す。操作量の将来の変化パターンを、数個の基本関数の組み合わせで表すことにより、計算負荷を低減するとともに、操作量を不必要に動かさないという利点を持つ。基本関数は、ステップ関数を必須として、その他は目標値(指令値)の次数に応じて必要により増やせば良いが、制御性能と計算負荷のバランスを考慮して、ステップ関数+ランプ関数とする。基本関数の数だけ、予測ホライズンが必要なので、2つの予測ホライズンHおよびH2を設定して、この2点で目標値と制御量が一致するように、操作量のステップ高さとランプ傾きを決定する。この計算は毎制御周期実行するので、実際に出力するのはステップ高さ分のみである。なお、図1には描いていないが、現在の偏差を予測ホライズン後に完全にゼロにすることを狙うのではなく、ある時定数でゼロに向かわせるための参照軌道の設定が可能である。参照軌道時定数により応答性とロバスト性のトレードオフを調整することができる。
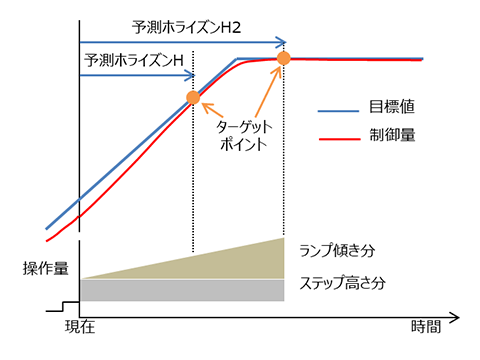
ところで、高度な制御方式の適用で制御性能が向上することが分っても、制御対象モデルの作成が難しいなどの導入障壁があると利用が広がらない 1)。そこで、従来は高度なスキルを必要としたモデル作成の自動化にも取り組んだ。
4.2 制御ループ構成
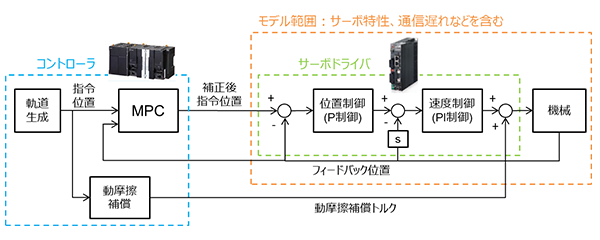
MPCを適用した位置制御ブロック図を図2に示す。制御対象モデルと将来の指令値を使用する高精度のフィードフォワード制御が特長であるが、フィードバック制御ループも有しており、モデル誤差や外乱の影響にある程度対応することができる。しかし、外乱への対応は高速フィードバックループを有するサーボドライバが主に担当する。このように、サーボドライバとコントローラ上のMPCが適切に役割を分担している。
MPCは非線形対象を扱う理論研究も進んでいる 9) が、計算負荷の増大は避けられないため、ここでは制御対象を線形としている。そのため、非線形特性が強くなると、制御性能が悪化する。具体的には動摩擦(クーロン摩擦)が該当し、速度反転直後や停止状態から動き出すときの追従遅れが大きくなる 10)。サーボドライバが持つ動摩擦補償機能は、一般にサーボドライバが受け取る位置指令値に基づいて速度方向を判定するため、コントローラ側で位置指令値をリアルタイムに補正する制御方式では適切に機能しない。そこで、補正前指令値に基づいて、コントローラ側で動摩擦補償を行う。
4.3 モデルの自動作成
対象モデルは1軸単位の1入力1出力線形モデルとする。したがって非常にシンプルなモデルであるが、それでも機械の設計情報から得られる特性は質量またはイナーシャだけであり、摩擦や固有振動などの特性を知ることは難しいため、システム同定手法 11)を採用する。動特性モデル形式は、モデル入力を指令位置、モデル出力を実位置とし、次の離散時間伝達関数とする。
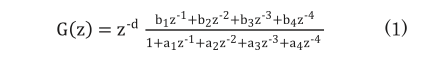
モデル作成用の応答データ例を図3に示す。最初に動摩擦トルクを測定し、次に適切なステップ速度を調べるための準備動作を行い、最後にトルクピーク値が飽和しない範囲で十分大きな値になるようなステップ速度を与えて、位置のランプ応答データを1往復分取得する。
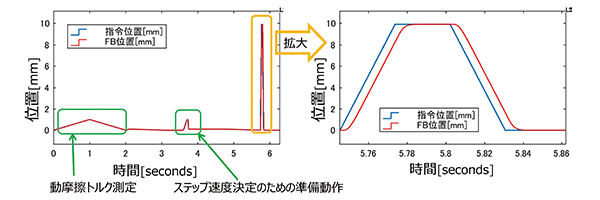
図3右側のランプ応答データにフィットする(1)式のパラメータを最小2乗法により推定する。伝達関数の次数は、高い精度を確保しながらも過剰適合を回避するために、最大4次として複数のモデル候補を作成し、最良の1モデルを選択する。選択基準は(2)式で計算する応答データへの適合率 12) の他に、モデルのインパルス応答をチェックし、逆応答など実際にはないはずの挙動を示すモデルを除外する。
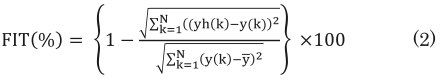
N:データ数、 y: 出力データ、 ‾y: 出力データの平均値、 yh: モデル出力データ
4.4 実機検証結果
ボールねじ駆動のXYステージ(図4)で実験を行った。フィードバック位置(実位置)は、サーボドライバ、コントローラ共に、リニアスケールから取得する。自動作成結果のモデルパラメータと自動設定した制御パラメータを表4に示す。予測ホライズンと参照軌道時定数もモデル特性に基づき自動設定する。コントローラの制御周期は0.5 msである。図5~8の実験結果比較において、従来制御方式を補正なしと表記している。サーボパラメータはオートチューニング結果を基に、軌跡制御の補正なしの場合のみ、両軸の位置ループゲインを小さい方(本実験ではX軸)に合わせている。またMPCの場合は、サーボドライバの速度フィードフォワード機能を無効化している。指令値に基づくフィードフォワード機能はMPCが担うためである。

| パラメータ | X軸 | Y軸 |
|---|---|---|
| d | 8 | 7 |
| a1 | -3.333485806286154 | -2.977750772048949 |
| a2 | 4.189151867233842 | 3.410571422347285 |
| a3 | -2.361822331916331 | -1.822152401743346 |
| a4 | 0.506442605663736 | 0.391218947429476 |
| b1 | 0.050952081980545 | 0.043199305733160 |
| b2 | -0.089291431420474 | -0.040339154707192 |
| b3 | 0.038625743495712 | -9.726898909130744e-04 |
| b4 | 0 | 0 |
| 正方向動摩擦トルク[%] | 12.42 | 9.52 |
| 負方向動摩擦トルク[%] | -11.12 | -9.22 |
| 予測ホライズンH | 2 | 2 |
| 予測ホライズンH2 | 4 | 4 |
| 参照軌道時定数[s] | 0.006 | 0.0055 |
徐々に速度を上げながら直径4 mmの円を連続描画する軌跡制御を行った。周速度約75 mm/sから最大周速度約126 mm/sの期間の補正なしとMPCの軌跡を図5に示す。補正なしでは速度が上がるに連れて、内回りの程度が拡大するために軌跡の線が太くなっているのに対して、MPCでは内回りの拡大を抑制できている。
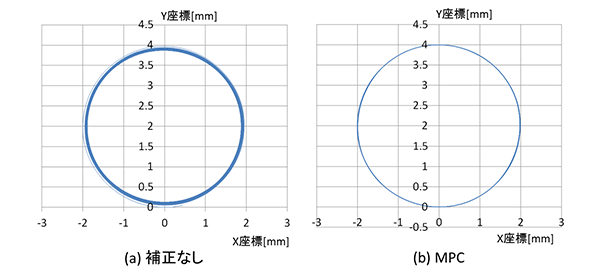
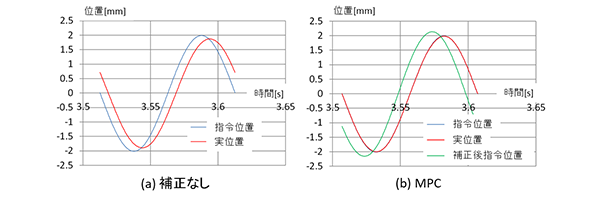
図5では指令位置に対する時間軸上での遅れは見えないので、図6に最大周速時1周期分のX軸データを示す。MPCの補正後指令位置は補正前の指令位置に対して先行し、かつ振幅が大きくなっている。この期間の最大位置偏差は、補正なしの744 µmに対して、MPCは17 µmであり、指令追従性が向上している。
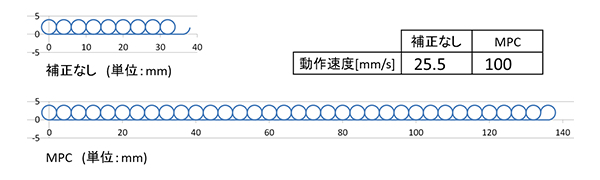
実際の加工では目標精度は決まっており、その精度をいかに短いタクトタイムで実現するかが期待効果になる。そこで、直径4 mmの円と長さ4 mmの直線を交互に等速で描く軌跡制御で、最大軌跡誤差が10 µm以下に収まる限界の動作速度を比較した。補正なしが速度25.5 mm/sで最大軌跡誤差9.1 µm、MPCが速度100 mm/sで最大軌跡誤差8.8 µmとなり、MPCの適用により動作速度を約4倍に向上することができた。図7に同一時間に動作できた軌跡(反時計周りで左から右へ進む)を示す。
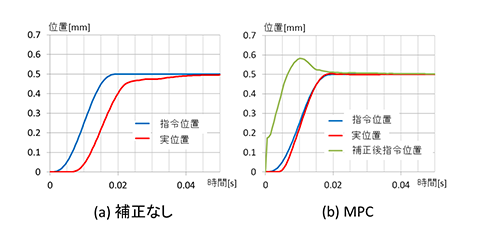
より多くの製造工程に適用可能な時間短縮例として、単軸ボールねじ(図4のX軸)の位置決め動作のデータを図8に示す。20 msで0.5 mmを移動する位置決めで、5次軌道とした。補正なしでは指令値に対して大きく遅れた状態のまま目標位置に到達するが、MPCでは目標位置に到達する前に指令値に追いついている。
5. ビジュアルフードバック制御のアライメントへの適用
5.1 ビジュアルフィードバック制御の概要
画像センサを使用してワークの位置合わせを行うアライメントは多くの組み立て工程に存在しているが、位置合わせの目標精度は製造物によって千差万別である。目標精度が高くないアライメントでは、1回の撮像でアライメントが完了するため、アライメント時間の短縮余地はほとんどない。一方、半導体やFPD(フラットパネルディスプレイ)などの目標精度がµmオーダーのアライメントの場合、画像系と機械系のキャリブレーション精度に依存するが、一般的には数回の撮像が必要であり、停止後の残留振動が収まるのを待って次の撮像を行うためアライメント時間が長く、時間短縮の余地が存在する。そこで、高精度アライメントを対象として、ビジュアルフィードバック制御によるアライメントの高速化に取り組んだ。
ビジュアルフィードバック制御は画像処理をフィードバック制御ループの中に組み込む制御手法であり、目標値の与え方により2種類に分類される 13)。目標値を位置(または距離や姿勢)で与える位置ベース法 14)と、画像の特徴量(例:領域の面積、線分の傾きなど)で与える特徴ベース法である。今回適用したのは位置ベース法である。なお、ビジュアルフィードバック制御はビジュアルサーボとも呼ばれる。
アライメント時間は、カメラ画像上の2つのアライメントマークが、開始時の離れた状態から目標精度の距離内に近づいて停止するまでに要する時間である。アライメントマークが2個の場合は両方が図9右側の状態になる必要がある。
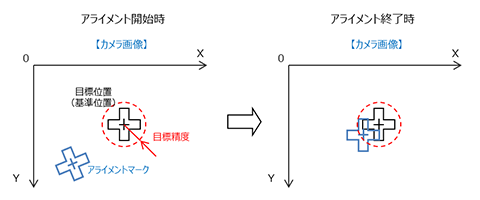
従来のアライメント動作を繰り返す手法は、停止後の残留振動が減衰するのを一定時間待ってから次の撮像を開始する。2013年にオムロンが開発したコンティニュアスアライメント 15) は、ワークを止めずに撮像を繰り返す方式で、停止に伴う残留振動の減衰待ち時間をなくすことでアライメントの高速化を実現した。軌道は検出距離が更新される度に新たに生成し旧軌道と接続するが、速度と加速度を指定する台形速度パターンを採用する点は従来方式と共通である。
ビジュアルフィードバック制御によるアライメントは、ワークを止めずに撮像を繰り返す点はコンティニュアスアライメントと同じであるが、サーボドライバへの位置指令生成にフィードバック制御を適用する点が異なる。これにより、制御周期毎にその時点の位置偏差に基づく速度指令および位置指令が計算され、より滑らかなステージ移動が可能となる。
5.2 制御ループ構成と技術内容
ビジュアルフィードバック制御適用アライメントの制御ブロック図を図10に示す。画像センサがアライメントマークの基準位置とのずれ量、すなわち距離と傾き角度を検出する。このずれ量に基づき、コントローラで各軸の必要移動距離を算出する。このとき、キャリブレーションパラメータを用いて、画像系座標から機械系座標への変換を行う。ここまでの処理は従来方式と同じである。
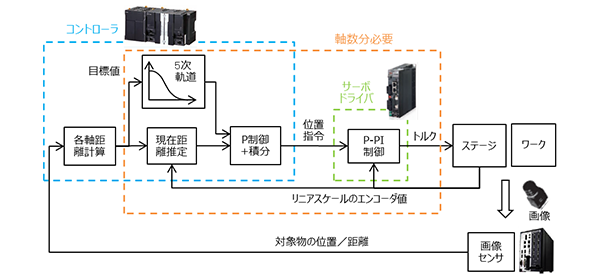
このあと、ステージの移動と停止に伴う被写体ブレおよび振動の抑制を狙い、ステージを滑らかに動かすために、主に4つの手法を採用している。
(1) 各軸サーボドライバへの指令速度(指令位置の微分値)がその時点の距離に応じて与えられるようP(比例)制御を採用する。比例ゲインはサーボドライバとステージのトータルの遅れ特性を測定して適切な値に設定する。
(2) 上記(1)のために、制御周期(例えば1 ms)毎に制御量が必要になるが、一般に画像センサの出力更新間隔は制御周期より長いため、検出距離が更新されない制御周期ではエンコーダ情報を使用して各軸の現在距離を推定する。
(3) 画像センサが検出する距離から算出される各軸移動量に基づいて、P制御の目標値(目標距離)を滑らかにゼロに近づける5次軌道を生成し更新する。この際、指令速度(指令位置の微分値)の急激な変化を回避するように旧軌道と接続する。
(4) 被写体ブレを抑制するため、ステージ速度が露光時間と目標精度から算出する速度上限値以下になることを撮像開始の条件に加える。
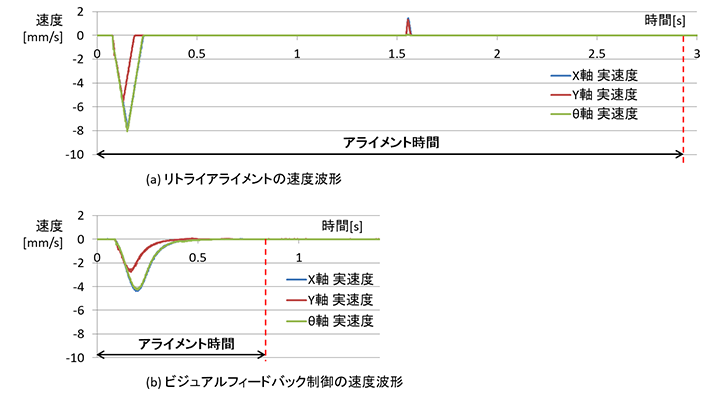
各軸の必要移動距離が、X軸: 0.6 mm、Y軸: 0.3 mm、θ軸: 0.6 mm(0.34°)の場合における、各軸の速度変化を図11に示す。グラフではX軸とθ軸の移動量が同じため、ほぼ重なっている。従来方式に対して、ビジュアルフィードバック制御の速度変化は滑らかである。このケースでの撮像回数は、従来方式が3回、ビジュアルフィードバック制御が9回である。
5.3 実機検証結果
ステージ機構XYθ、2カメラ構成の図12に示すアライメント装置で、精度±1 µmのアライメント時間を従来方式と比較した。初期位置をX軸:±0.6 mm、Y軸:±0.3 mm、θ軸:±0.34°の範囲内で乱数により生成して1000回のアライメントを実行した結果を表5に示す。コントローラの制御周期は1ms、画像センサの露光時間は20 ms、位置計測の平均時間間隔は約60 msである。キャリブレーションパラメータはオートキャリブレーション機能で決定した値を使用した。

| 方式 | 平均 | +3σ | 最大 |
|---|---|---|---|
| 従来方式 | 3.08 | 3.91 | 5.64 |
| コンティニュアスアライメント | 2.14 | 3.59 | 3.58 |
| ビジュアルフィードバック制御 | 0.75 | 1.00 | 1.14 |
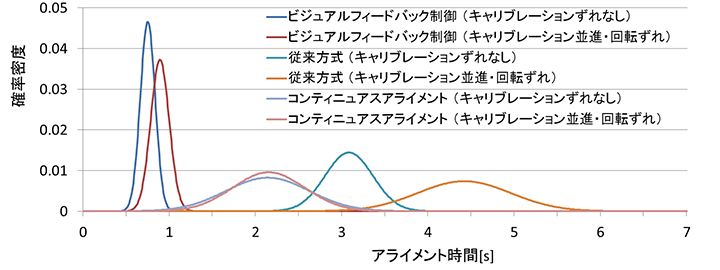
ビジュアルフィードバック制御方式は、従来方式比で平均値が約1/4.1に、コンティニュアスアライメント比で平均値が約1/2.9にアライメント時間を短縮している。図13はアライメント時間が正規分布に従うと仮定した分布(横軸の刻み:0.01 s)であり、キャリブレーションパラメータを並進方向(X方向、Y方向とも1 mm)と回転方向(5°)の両方向に意図的にずらした場合の分布も併せて示す。キャリブレーションパラメータをずらした場合のアライメント時間の延びは、平均値で0.14 s、+3σが0.21 sに収まっている。このことは経年変化等によるキャリブレーションパラメータのずれに対してロバスト性が高いことを意味しており、安定したアライメント動作を長期間維持できる可能性がある。
6. 結言
制御システムを構成するILOの摺り合わせ制御技術として、モデル予測制御の位置制御への適用例と、ビジュアルフィードバック制御のアライメントへの適用例を報告した。両事例で、ものづくりの製造工程においてタクトタイム短縮に貢献できる効果を確認できた。今後両制御技術の適用範囲の拡大とともに、新しいILO摺り合わせ制御技術の開発にも取り組み、引き続き、ものづくりの革新に貢献していく所存である。
参考文献
- 1)
- 鶴原吉郎, 岩澤尚俊. メカニカルシステムにおける制御技術動向. 計測と制御. 1999, Vol.38, No.1, p23-30.
- 2)
- 小黒龍一. ロボット・工作機における制御理論応用. 計測と制御. 1999, Vol.38, No.1, p42-46.
- 3)
- 稲葉肇. 実用化に向けての制御理論の新たな展開. 計測と制御. 1999, Vol.38, No.1, p4-9.
- 4)
- S. Joe, Qin; Thomas, A. Badgwell. A survey of industrial model predictive control technology. Control Engineering Practice. 2003, Vol.11, Issue7, p733-764.
- 5)
- Jacques, RICHALET. WHY PREDICTIVE CONTROL?. 計測と制御. 2004, Vol.43, No.9, p.654-664.
- 6)
- ジャック・リシャレ, 江口元, 小崎恭寿男(監修). モデル予測制御-PFCの原理と応用-. 日揮, 2007, 255p.
- 7)
- 藤田穣, 中村恵子, 鈴木俊太郎. モデル予測制御の機械制御への適用. IHI技法. 2011, Vol.51, No.2, p33-37.
- 8)
- 小山正人, 長野鉄明. 規範モデルを用いた電動機の2自由度位置制御. 電気学会論文誌D. 1994, Vol.114, No.2, p.137-143.
- 9)
- 大塚敏之. 非線形モデル予測制御の研究動向. システム/情報/制御. 2017, Vol.61, No.2, p42-50.
- 10)
- 松原厚. 精密位置決め・送り系設計のための制御工学. 森北出版, 2008, p185-198.
- 11)
- 足立修一. MATLABによる制御のためのシステム同定. 東京電機大学出版局, 1996, 202p.
- 12)
- 足立修一. MATLABによる制御のための上級システム同定. 東京電機大学出版局, 2004, p5-22.
- 13)
- 橋本浩一. ビジュアルサーボ-Ⅰ -ビジュアルサーボとは. システム/情報/制御. 2009, Vol.53, No.9, p411-416.
- 14)
- 橋本浩一. ビジュアルサーボ-Ⅳ -位置ベースビジュアルサーボ. システム/情報/制御. 2010, Vol.54, No.3, p117-123.
- 15)
- オムロン. 制御システムおよび制御方法. 特許第6167622号. 2017-07-26.















