ILO integrated control technology
- ILO integrated control technology
- Machine automation controller
- Model predictive control
- Visual feedback control
- Control theory
To solve various control problems in the manufacturing process, Omron pursues advanced integrated control technology of Input-Logic-Output (ILO). In addition to providing ILO devices capable of high-speed and highprecision measurement and control, we also provide libraries of control applications based on control theory and cooperative operation of ILO devices.
In this paper, as an example of application of control theory, we report the outline and effect of the position control method realizing high accuracy command following performance by Model Predictive Control (MPC). With the circular continuous trajectory control by X-Y stage, the operation velocity of about 4 times that of the conventional control method has become possible for achieving the same locus precision. It has a function to automatically create a control target model, and it has features to be easily used as well. In addition, as an example of cooperative operation of ILO devices, we give an outline of high speed alignment by visual feedback control and an example of effect. In this method, the position of the object is aligned while repeating the position measurement by image sensors without stopping the workpiece, and compared with the conventional method in which the image is taken after the work is stopped, the alignment time with the target accuracy of ┬▒ 1 ╬╝m could be shortened to about 1/4. It also has the feature of being robust to the deviation of the calibration parameters of the coordinate transformation of the image system and the mechanical system.
1. Introduction
In recent years, there have been rapid changes in manufacturing, particularly with regards to digital products such as smart phones and electric vehicles where development have been strongly promoted. As a result, the expectations for control technology are increasing daily. This paper describes control problems that arise in manufacturing processes, excluding design. These processes include machining, assembly, conveyance, inspection, etc.
There is continuing microminiaturization of components for digital products, such as semiconductors and other electronic parts. At the same time, greater accuracy is required while high productivity is maintained for all processes of machining, assembly, and inspection. Furthermore, it is necessary to limit the contact load during assembly to small value increases so as to avoid damage to parts with the advancement of microminiaturization. Higher accuracy and small contact loads can be sometimes achieved by decreasing the machining and assembly speeds. However, the challenge is to balance this with the increase in takt time.
Although the demands of cutting-edge technology have conventionally been satisfied by control systems uniquely developed by equipment manufacturers, improvements in the performance and functions of industrial multi-purpose controllers provide more opportunities for the application of programmable logic controllers (PLCs) and motion controllers. In order to meet this expectation, we report control technology based on the high-level integration of sensing instruments (Input), controllers (Logic), and drive apparatus (Output).
2. Control problems in manufacturing
There are various control problems for each combination of manufacturing items and processes. They can be classified as accuracy, productivity, or cost, as shown in Table 1. There are multiple expressions for accuracy depending on the controlled variable, but deviation from a command value or target value should be minimized. These three types of problems have a trade-off relationship and it is important to understand how they can all be optimized. For example, in trajectory control, reducing the operating speed enables the accuracy of the trajectory control to be improved, but this does not solve the problem. As the target accuracy is normally predetermined for each product, we consider how much the operating speed can be increased within the range that provides the required accuracy. However, the possible necessity of expensive measuring and control instruments or a considerable number of man-hours for tuning means that this may not provide a realistic solution.
| Control quantity | Accuracy | Productivity | Cost |
|---|---|---|---|
| Position and distance | Positioning accuracy, trajectory accuracy, alignment accuracy, vibration suppression, multi-axis synchronization accuracy, and overshoot suppression | Improvement of operating speed Reduction of settling time |
Reduction of adjustment man-hours Cost reduction |
| Velocity | Stability and multi-axis synchronization accuracy | ||
| Load, tension, and temperature | Stability, overshoot suppression, and multi-point uniformity |
In addition, the factors that make the solution of control problems difficult, as shown in Table 2, must be addressed. This is the role of Input-Logic-Output (ILO) integrated control technology.
| Due to control object | Disturbance (non-regular form and regular form), low rigidity of machine, characteristic change (machine difference and secular change), load fluctuation, workpiece tolerance, non-linear characteristics (including friction, dead zones, and hysteresis), dead time, and interference |
|---|---|
| Due to control system | Insufficient measurement performance (responsiveness and resolution), insufficient operation performance (control cycle), dispersion of input/output response time due to non-synchronization between ILOs, calibration error between ILOs, and dead time due to communication time and control cycle |
3. ILO integrated control technology
Omron provides measuring and control instruments with high accuracy and speed such as FH series visual sensors, ZW series displacement sensors (Input), NJ/ NX/NY series machine automation controllers (Logic), and 1S/G5 series servo drivers (Output). Control systems with a maximum speed of 125 ╬╝s/8-axis and synchronization accuracy between axes of 1 ╬╝s can be constructed by connecting these instruments with a field network EtherCAT®, which enables high accuracy synchronization. Further, a programmable multi-axis motion controller PMAC (Logic) enables ultra-high speed control cycle of the maximum speed, 16.6 ╬╝s/ 1-axis and 50 ╬╝s/8-axis, by connecting the input/ output equipment with analog signals.
The higher speed and accuracy of ILO equipment are effective for the alleviation of factors due to the control system shown in Table 2; however, in many cases they are ineffective for the alleviation of factors due to the control object. For example, when improvement of the command following of a control object with a large response delay is desired, even speeding up the control cycle of the controller or servo driver is ineffective. In addition, if the difference of the response delay between axes is large, even higher synchronization accuracy of the output of each axis cannot guarantee sufficient improvement of the synchronization accuracy of the mechanical operation. The best method is to improve the characteristics of the machine; it is important to apply appropriate control theory considering the characteristics of the machine as the control response. When control theory is applied to multi-purpose controllers, such as PLCs, it often covers only up to proportional-integral-derivative (PID) control. This is due to the difficulty of modeling the characteristics of the control object, which are required for high-level control, because of the incapability of identifying the control object and the difficulty in adjusting control parameters that are different for each control theory 1). As the dedicated controller for specific equipment can completely identify the characteristics of a machine, the application of advanced control theory based on a control object model is allowed to progress 2) 3). Furthermore, machine vendors commonly apply advanced control theory through user programs with the PLCs.
In addition, it is important to avoid restricting each piece of ILO equipment by combining them effectively. For example, the measurement accuracy and range of a displacement sensor have a trade-off relationship; therefore, repositioning the sensor improves the measurement range of high accuracy measurement since the distance between the displacement sensor and workpiece falls within the measurement range found by applying profiling control to this relation.
The main control technologies that have been developed so far, and examples of their effects, are shown in Table 3:
| Control technology | Example of effect |
|---|---|
| Vibration suppression control | Improvement of conveying speed, suppression of vibration and tilt of liquid level |
| Learning control | Improvement of trajectory accuracy, reduction of positioning time |
| Model predictive control (MPC) | Improvement of trajectory accuracy,reduction of positioning time |
| Sliding mode control | High robustness against load fluctuation |
| Impedance control | Suppression of contact load overshoot |
| External force estimation | Low tension conveying of web |
| Visual feedback control | Reduction of alignment time, high robustness against calibration error |
| Spectral resolution control | Improvement of machining accuracy and speed by cooperative operation of actuators with different response speeds |
| Predictive synchronization control | Improvement of synchronization accuracy of multi-axis |
| Profiling control | High accuracy measurement of two-dimensional shapes using a displacement sensor |
This paper outlines and provides examples of the effects of a position control system that realizes high accuracy command following performance using model predictive control (MPC) as an example application of control theory. In addition, it outlines and provides examples of the effects of high speed alignment by visual feedback control as an example of cooperative operation of ILO equipment.
4. Application of MPC to position control
4.1 Outline of MPC
Improvements to the following to command value, suppression of vibration, or reduction of the influence of disturbance, etc. are considered to be methods of reducing machining takt time that take control technology as a starting point, their necessity and importance vary depending on the equipment and process. This paper reports on the application of MPC for position control that is effective at improving the following to command value, which is the most basic performance. Although MPC has been successful in a large number of applications and prevails in the field of process control 4), examples of its application in motion control are not so widely found. One reason for this is the magnitude of the calculation load, that is to say, methods with a low calculation load, such as predictive functional control (PFC) 5) 6), must be adopted for MPC and the results of the application to force control of press equipment 7) have been reported. Another reason is that prediction in MPC is very effective when the characteristics of the control object include large dead time and delay, but the short dead time and delay in motion control is considered to give only small expectations in this point. However, in constructions where the connection between the ILOs is performed by communication, the response delay of a machine is added with the communication delay (dead time). In addition, if the requirement for command following performance is high, the following delay of the feedback value against the command value is a problem from the viewpoint of the controller that generates the command value. Therefore, we focused on the improvement of the command following performance and applied MPC to position control in the motion control region. The model following type two degree of freedom control 8) based on PID control is known as a servo control system and provides good control performance. We adopted MPC by considering that expressly considering dead time and using the future command value are important points of capability.
MPC repeats the process of determining the future manipulated variable pattern using a control object model so that the control condition of a finite section, called the prediction horizon, is optimum and actually provides the manipulated variable only for the first control cycle.
Fig. 1 shows a conceptual diagram of the manipulated variable calculation in PFC. It has the advantage that the expression for the future change pattern of the manipulated variable is a combination of several basic functions; this reduces the calculation load, and the manipulated variable is not moved unnecessarily. The basic functions are essentially the step function and others that can be increased if necessary depending on the degree of the set point (command value). We adopt a step function + ramp function considering the balance between the control performance and calculation load. Since the required number of prediction horizons corresponds to the number of basic functions, two prediction horizons, H and H2, are set, and the step height and the ramp slope are determined so that the set point and controlled variable coincide at these two points. As this calculation is implemented in each control cycle, the actual output is for step height only. In addition, although it is not shown in Fig. 1, the main aim is not to make the current deviation equal to zero after the prediction horizon, although it is possible to set the reference orbit to direct it to zero at a certain time constant. The time constant of the reference orbit enables the trade-off between responsiveness and robustness to be adjusted.
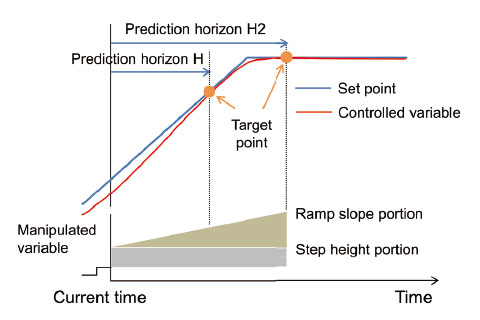
It is worth noting that even if we know the improvement in the control performance when an advanced control system is applied; there are possible barriers to introduction such as difficulty in creating a control object model, which disturbs the popularization of utilization 1). Therefore, we also approached the automation of model generation that conventionally required advanced skill.
4.2 Construction of control loop
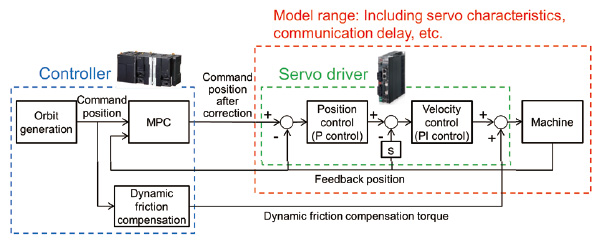
A position control block diagram applied using MPC is shown in Fig. 2 The advantage of this is that it is a highly accurate feed- forward control using a control object model and the future command value; in addition, it can partially deal with the influence of model error and disturbance because it has a feedback control loop. However, the servo driver, which has a high-speed feedback loop, mainly deals with disturbance. Therefore, the servo driver and MPC on the controller share the role appropriately.
In MPC, although the theoretical research regarding non-linear objects is advanced 9), the control object here is assumed to be linear because the increase in the calculation load is unavoidable. Therefore, strong non- linear characteristics deteriorate the control performance. Specifically, this is related to dynamic friction (Coulomb friction), and increases in the follow-up delay directly after reversing movement or getting out movement form stop conditions 10). The dynamic friction compensation function of the servo driver generally judges the rotation direction based on the position command value received by the servo driver; hence, the function does not work properly in control systems that compensate for the position command value at the controller side in real time. Therefore, dynamic friction compensation is performed at the controller side based on the pre-correction command value.
4.3 Automatic generation of the model
An object model is assumed to have 1 input and 1 output that are linear for each axis. Therefore, even though this is a very simple model, the system identification technique 11) is adopted because only the mass or inertia characteristics are obtained from the information about the machine design and it is difficult to know characteristics such as friction or natural frequency. Dynamic characteristics model types assume that the model input is the command position and that the model output is the actual position, this is expressed by the discrete time transfer function shown below:
-
(1)
An example of the response data used to create a model is shown in Fig. 3 The ramp response data for both ways are obtained by first measuring dynamic friction torque, then performing the preparation operation to investigate the proper step velocity, and finally giving a step volocity that has a sufficiently large value within the range without saturating the torque peak value.
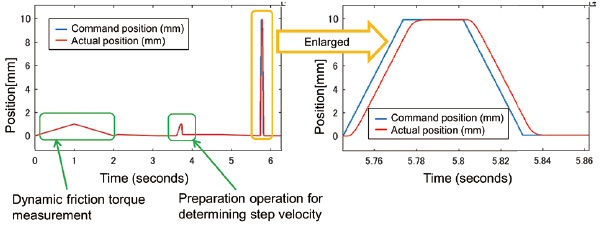
The parameter of formula (1) that fits the ramp response data at the right side of Fig. 3 is estimated using the least square method. Assuming that the maximum degree of the transfer function is 4, in order to avoid overfitting while securing high accuracy, multiple model candidates are created and the best one selected. Selection criteria check the impulse response of the model, the ratio of the fitting 12) to the response data calculated by formula (2), and exclude models that show unrealistic behavior such as an inverse response.
-
(2)
N: Number of data, y: Output data, ╠ģy: Average of output data
yh: Model output data
4.4 Result of verification using a real machine
Tests were conducted on an X-Y stage driven by a ball screw (Fig. 4). The feedback positions (actual positions) of the servo driver and controller were obtained from a linear scale. Model parameters resulting from automatic generation and automatically set controls are shown in Table 4 The prediction horizon and time constant for the reference orbit were also set automatically based on the model characteristics. The control cycle of the controller was 0.5 ms. In the comparison of test results, shown in Figs. 5 through 8, the conventional control system is described as without correction. For the servo parameter, the position loop gain of both axes is made to match the smaller one (X-axis in this test) only in case of trajectory control without correction based on the result of auto-tuning. Further, in case of MPC, the velocity feed forward function of the servo driver is invalidated because command based feed forward function is bore by MPC.

| Parameter | X-axis | Y-axis |
|---|---|---|
| d | 8 | 7 |
| a1 | -3.333485806286154 | -2.977750772048949 |
| a2 | 4.189151867233842 | 3.410571422347285 |
| a3 | -2.361822331916331 | -1.822152401743346 |
| a4 | 0.506442605663736 | 0.391218947429476 |
| b1 | 0.050952081980545 | 0.043199305733160 |
| b2 | -0.089291431420474 | -0.040339154707192 |
| b3 | 0.038625743495712 | -9.726898909130744e-04 |
| b4 | 0 | 0 |
| Friction torque in positive direction [%] | 12.42 | 9.52 |
| Friction torque in negative direction [%] | -11.12 | -9.22 |
| Prediction horizon H | 2 | 2 |
| Prediction horizon H2 | 4 | 4 |
| Time constant for reference orbit [s] | 0.006 | 0.0055 |
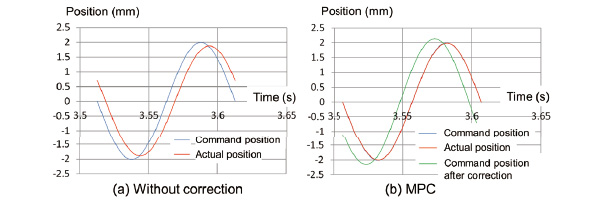
Trajectory control that continuously drew a circle with diameter of 4 mm while gradually increasing the velocity was performed. This went from an approximate circumferential velocity of 75 mm/s to a maximum of 126 mm/s. The trajectories without correction and of the MPC are shown in Fig. 5 For the circle without correction, the line of the trajectory is thicker as the velocity increases because there is a greater degree of inward turning. On the other hand, for MPC, the increase in the inward turning is successfully suppressed.
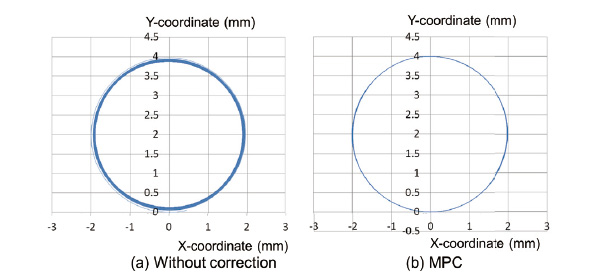
As the delay on the time axis against the command position is not shown in Fig. 5, the X-axis data corresponding to one cycle at the maximum circumferential velocity is shown in Fig. 6. The command position of the MPC after correction is precedent to that before correction and has larger amplitude. The maximum positional deviation during this period without correction was 744 ╬╝m while that for the MPC was 17 ╬╝m, showing an improvement in the command following.
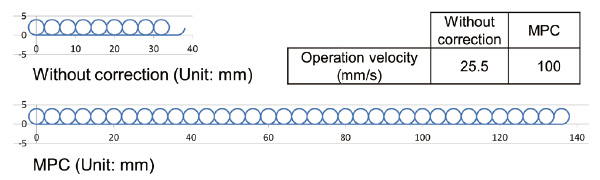
For real machining, the target accuracy is already determined, and the minimum takt time required to achieve this accuracy is an expected effect. Therefore, in the trajectory control that alternately draws a circle with a diameter of 4 mm and a straight line 4 mm long at equal velocity, the maximum operation velocity where the maximum trajectory error is less than 10 ╬╝m were compared. A maximum trajectory error of 9.1 ╬╝m was observed at a velocity of 25.5 mm/s without correction and 8.8 ╬╝m at a velocity of 100 mm/s for the MPC, meaning that the application of the MPC improved the operation velocity by approximately a factor of four. Fig. 7 shows the trajectories that could act in the same time (advance from the left to the right counterclockwise).
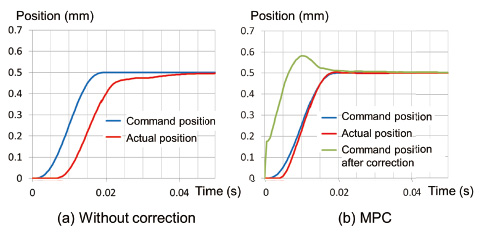
Data for the positioning operation of a single axis ball screw (X-axis in Fig. 4) are shown in Fig. 8 as an example of time reduction applicable to a larger number of manufacturing processes. Positioning, in which a movement of 0.5 mm was performed in 20 ms, was provided with a 5-degree orbit. Although, in the case without correction, the actual position reached the target position in the condition where it was greatly delayed compared to the command value; in case of the MPC, the actual position caught up with the command value before arriving at the target position.
5. Application of visual feedback control to alignment
5.1 Outline of visual feedback control
Alignment using an visual sensor to position a workpiece is performed in many assembly processes; the target accuracy of the positioning varies significantly depending on the product. Since alignment with lower target accuracy can be completed with only one imaging, the allowance for alignment time reduction is only small. On the other hand, in case where the target accuracy of is in the order of ╬╝m, such as in semiconductors or FPDs (flat panel displays), it is dependent on the calibration accuracy of the image and machine systems. Generally speaking, since the imaging must be repeated several times and each imaging is performed after stopping and waiting for the attenuation of residual vibrations, the alignment time is long, providing the opportunity for time reduction. Therefore, we aimed to speed-up the alignment by using visual feedback control for high accuracy alignment.
Visual feedback control is a control technique in which image processing is incorporated with the feedback control loop, there are two types depending on how the target value is given 13). The first one is a position based method 14) that gives the target value as position (or distance, or posture), and the second is a feature based method that gives it as feature quantity (e.g. area of a region, or slope of line). We applied the position-based method. The visual feedback control is also called the visual servo.
The alignment time is the time required for the action that aligns two marks on a camera image within the target accuracy, going from the distant condition at the start and stops. In case of two alignment marks, both marks are in the condition shown by the right diagram in Fig. 9.
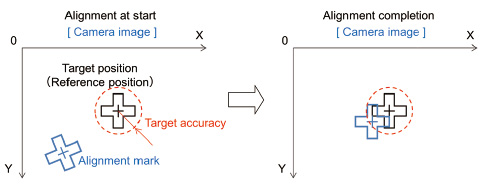
The conventional technique of repeating the alignment operation starts the next imaging process after waiting a given time after stopping until residual vibrations have attenuated. Continuous alignment 15), developed by Omron in 2013, is a system that repeats the imaging without stopping the workpieces; hence, there are no vibrations caused by stopping and the need for the attenuation waiting time is eliminated and the alignment speed is increased. A new orbit is generated each time the detected distance is updated and this connected to the old orbit; as in the conventional system, a trapezoidal velocity pattern is adopted for which the velocity and acceleration are specified.
Although alignment by visual feedback control is same as continuous alignment from the perspective of repeating imaging without stopping workpieces, it is not same from the perspective of applying the feedback control from the generation of the position command to the servo driver. Thus, the velocity and position commands based on the positional deviation at that time are calculated for each control cycle, enabling smoother stage movement.
5.2 Construction of control loop and content of technology
A control block diagram of the alignment applied using a visual feedback control is shown in Fig. 10 The visual sensor detects the amount by which an alignment mark shifts from the reference position, i.e. the distance and inclination angle. The distance of the movement required is calculated by the controller for each axis based on this shift amount. At this time, the transformation from the image base coordinate to the machine base coordinate is completed using the calibration parameter. Processing so far is the same as that of the conventional system.
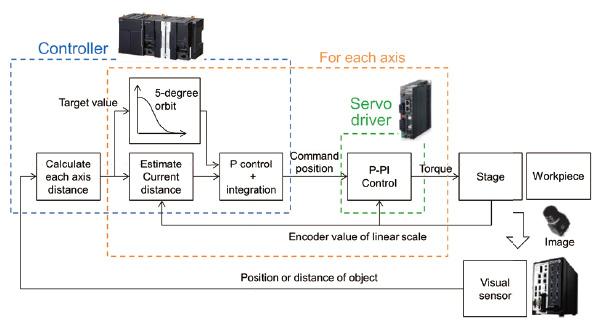
Hereafter, four main techniques are adopted to suppress subject shake and vibration due to the movement and stopping of the stage, and to move the stage smoothly.
(1) Adopt P (proportion) control so that the command velocity (derivative of the command position) is given corresponding to the distance at that time. Set the proportional gain to the proper value after measuring the total delay characteristics of the servo driver and stage.
(2) Control amount is required for each control cycle (e.g. 1 ms), as described in (1). As the output updating interval is generally longer than the control cycle, estimate the current distance using encoder information in the control cycle in which the detected distance is not updated.
(3) Generate and update the 5-degree orbit such that the target value (target distance) of P control smoothly approaches zero based on the moving amount of each axis calculated from the distance detected by the visual sensor. At this time, connect to the old orbit so as to avoid a sudden change in the command velocity (derivative of the command position).
(4) In order to suppress subject blur, add the condition for the imaging start when the stage velocity is not more than the upper limit for the velocity calculated from the exposure time and target accuracy.
The velocity change of each axis, when the required moving distance for each axis is 0.6, 0.3, and 0.6 mm (0.34┬░) for the X-, Y-, and


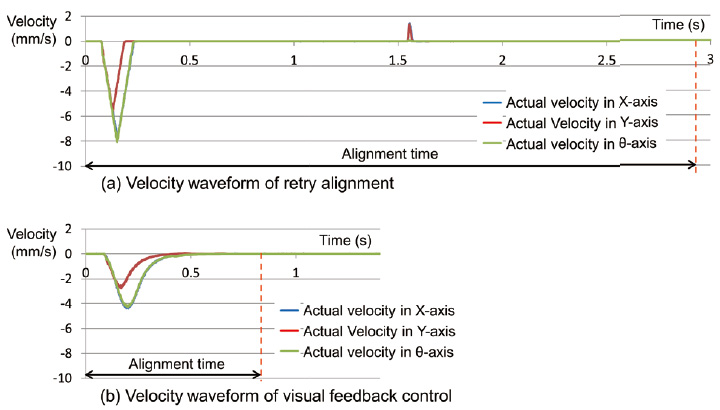
5.3 Result of verification using a real machine
The alignment time with accuracy of ┬▒1 ╬╝m was compared with that of a conventional system using the alignment equipment with an X-Y-


| System | Average | +3Žā | Max. |
|---|---|---|---|
| Conventional system | 3.08 | 3.91 | 5.64 |
| Continuous alignment | 2.14 | 3.59 | 3.58 |
| Visual feedback control | 0.75 | 1.00 | 1.14 |
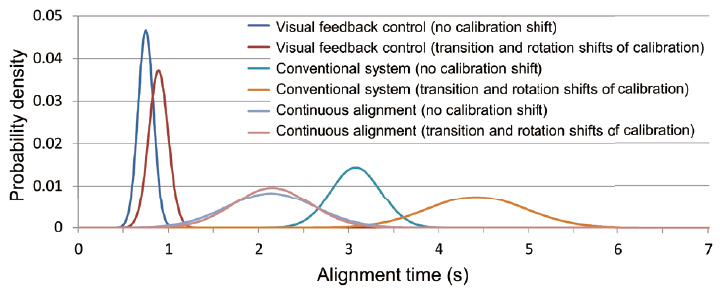
In the visual feedback control system, the average alignment time is reduced to approximately 1/4.1 of that of the conventional system, and to approximately 1/2.9 of continuous alignment. Fig. 13 shows the distribution (increment of the horizontal axis: 0.01 s) assuming that the alignment time is subject to normal distribution, and also shows the distribution when the calibration parameter was intentionally shifted in the translation directions (1 mm in both the X and Y directions) and in the rotation direction (5┬░). The increase in the alignment time when the calibration parameter was shifted is less than 0.14 s on average and 0.21 s for +3Žā. This means that the system is robust against the shift of the calibration parameter due to secular change, etc. and it is possible that stable alignment operation may be maintained for a long time.
6. Conclusion
We have reported an example of the application of model predictive control for position control, and an example of the application of visual feedback control for alignment as a control system composed of ILO integration control technology. Both cases were shown to be capable of contributing to the reduction of takt time in manufacturing processes. We hereafter intend to extend the application range of both control technologies, approach the development of new ILO integration control technology, and contribute to the innovation of manufacturing continuously.
References
- 1)
- Yoshiro Tsuruhara, Naotoshi Iwazawa. A Control Technology Survey for Mechanical System Development. Journal of the Society of Instrument and Control Engineers. 1999, Vol.38, No.1, p.23-30.
- 2)
- Ryuichi Oguro. Control Methods for Industrial Robot and NC Machine . Journal of the Society of Instrument and Control Engineers. 1999, Vol.38, No.1, p.42-46.
- 3)
- Hajime Inaba. Control Theory...Dynamic Evolution for Feasible Implementation. Journal of the Society of Instrument and Control Engineers. 1999, Vol.38, No.1, p.4-9.
- 4)
- S. Joe, Qin; Thomas, A. Badgwell. A survey of industrial model predictive control technology. Control Engineering Practice. 2003, Vol.11, Issue7, p.733-764.
- 5)
- Jacques, RICHALET. WHY PREDICTIVE CONTROL?. Journal of the Society of Instrument and Control Engineers. 2004, Vol.43, No.9, p.654-664.
- 6)
- Jacques Richalet, Hajime Eguchi, Yasuo Kozaki (Supervision). Model Predictive Control: Principles and Applications of Predictive Functional Control. JGC CORPORATION, 2007, p.255.
- 7)
- Joe Fujita, Keiko Nakamura, Shuntaro Suzuki. Application of Predictive Functional Control to servo- mechanical system. Journal of IHI technologies. 2011, Vol.51, No.2, p.33-37.
- 8)
- Masato Koyama, Tetuaki Nagano. Two Degrees of Freedom Position Control using Reference Model for Motor Drives. IEEJ Transactions on Industry Applications. 1994, Vol.114, No.2, p.137-143.
- 9)
- Toshiyuki Ohtsuka. Research Trend of Nonlinear Model Predictive Control. SYSTEM, CONTROL AND INFORMATION. 2017, Vol.61, No.2, p.42-50.
- 10)
- Atsushi Matsubara. Control Engineering for Precision Positioning and Feeding System Design. Morikita Publishing Co., Ltd., 2008, p.185-198.
- 11)
- Shuichi Adachi. System identification for control by MATLAB. Tokyo Denki University Press, 1996, p.202.
- 12)
- Shuichi Adachi. Advanced system identification for control by MATLAB. Tokyo Denki University Press. 2004, p.5-22.
- 13)
- Koichi Hashimoto. Visual Servo-I : What is Visual Servo?. SYSTEM, CONTROL AND INFORMATION. 2009, Vol.53, No.9, p.411-416.
- 14)
- Koichi Hashimoto. Visual Servo-IV : Position-based Visual Servo. SYSTEM, CONTROL AND INFORMATION. 2010, Vol.54, No.3, p.117-123.
- 15)
- OMRON Corporation. CONTROL SYSTEM AND CONTROL METHOD. Patent Number 6167622. 2017-07-26. (US9424646. 2016-08-23)
The names of products in the text may be trademarks of each company.
















