機械学習を活用した経路計画技術
経路計画は、環境中において与えられたスタートからゴールまでの障害物と衝突しない経路を出力する問題であり、モバイルロボットの自律移動におけるグローバルプラニングやマニピュレータの動作計画など、様々な分野において広く取り組まれている。このような経路計画問題に対して、機械学習を活用することで性能の向上を図る取り組みが近年多く報告されている。本稿では機械学習ベースの経路計画技術についていくつかの代表的アプローチを紹介するとともに、著者らの最近の取り組みである深層学習ベースのA*探索技術(Neural A*)について詳細に解説する。
1. まえがき
経路計画(path planning, pathfinding)は人工知能分野やロボティクス分野において古くより取り組まれる基本的問題である。いま、図1aのように障害物のある環境を考える。経路計画は、この環境において与えられたスタート地点からゴール地点に至るまでの、障害物に衝突しない最短の移動経路(path)を出力する問題である。たとえばモバイルロボットや自動運転車両の自律移動といったシナリオでは、環境としてSLAM等で獲得された障害物の地図、スタート・ゴール地点としてはその地図上における自律移動体の現在・目的地を考えることになる。あるいはロボットマニピュレーションの分野では、環境としてロボットの関節の状態等で定義されるコンフィギュレーション空間、スタート・ゴール地点としてロボットの開始・目標状態が与えられることになる(このような問題はしばしば動作計画、motion planningと呼ばれ経路計画と区別される)。いずれの状況においても、経路問題を解くことによって、我々はロボットを安全かつ短時間で所望の状態に移動させることが可能となる。
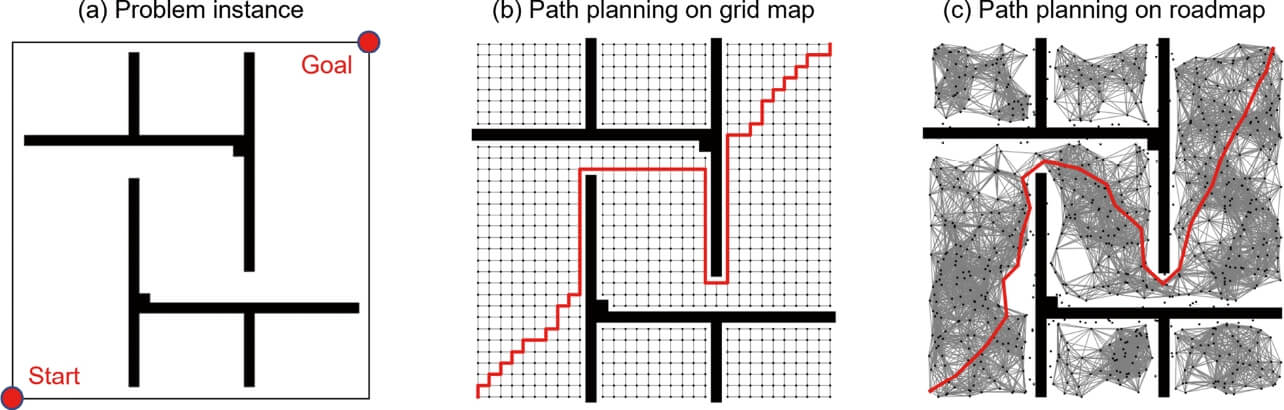
経路計画技術は、環境をどのように表現するか、またその表現された環境において経路をどのように探索するかという観点で、いくつかの種類に分類することができる。たとえばモバイルロボットの経路計画においては、図1bのように環境を格子地図に離散化したうえで4近傍や8近傍のグラフとして表現し、A*探索や最良優先探索といったグラフ探索アルゴリズムによってスタート地点からゴール地点への最短経路を探索することが一例として挙げられる。ロボットの移動する環境が非常に広域である場合、あるいはロボットマニピュレーションのように環境が高次元空間である場合は、図1cのように環境中でランダムに選択された地点をつないだグラフ(ロードマップ)を構築したうえで経路計画をすることや、スタート地点からゴール地点に向かって逐次的に次の移動候補地点を選択しつつ経路計画をすることがある。いずれの場合も、環境を細かい格子地図や多数地点から構成されるロードマップで表現することによって経路計画の成功率や得られる経路長を改善することができるが、それにともなって経路計画の計算コストも増大する。すなわち、経路計画の性能とその計算コストはトレードオフの関係にある。
これに対して近年、機械学習技術を活用することによってこのトレードオフを改善する研究が活発に進められている。直感的には、経路計画の問題インスタンス(環境、スタート、ゴールの組合せ)とその解(スタートからゴールまでの経路)の組を学習データとして用意し、その関係を何らかの機械学習モデルにより学習する。これにより、新たな問題インスタンスに対して学習済みモデルを適用することで、解となる経路を効率的に計画するための手がかりを得ることができる。あるいは、典型的な経路計画技術では環境中における障害物の位置は既知である必要があるが、未知の環境に対して機械学習モデルを適用することで障害物の配置を推定し、それに基づいて経路計画を実行することもできる。本稿ではこのような機械学習を活用した経路計画に関していくつかの代表的な技術を紹介するとともに、著者らの近年の成果である深層学習ベースのA*探索について詳しく解説する。
2. 機械学習を活用した経路計画技術
前節で述べた通り、経路計画技術を分類する一つの基準として環境の表現方法がある。以下では、環境を格子地図に離散化した探索ベースの経路計画およびランダムに選択された地点をつないだロードマップを用いるサンプリングベースの経路計画について、機械学習を活用した事例を紹介する。
2.1 機械学習を活用した探索ベース経路計画
格子地図上での経路計画は、しばしばA*探索や最良優先探索が利用される。いずれのアプローチも、格子地図を4近傍や8近傍のグラフとして表現し、スタート地点からゴール地点まで最短経路を逐次的に探索する。いま、グラフを





上記の問題に対して、探索ベース経路計画は一般に以下のアルゴリズムに基づいて行われる。
Algorithm 1: Search(G , c , 

- 1:
- Initialize
- 2:
- While
do
- 3:
- Select
based on the criterion
- 4:
- Update
- 5:
- Extract
- 6:
- Update
- 7:
- Foreach
do
- 8:
- Update
- 9:
- Endfor
- 10:
- Endwhile
- 11:
- Compute P ← Backtrack(Parent,
)
- 12:
- Return P
ここで、探索の進捗はオープンリストO とクローズドリストC と呼ばれる二種類のリストによって管理される。オープンリストには解経路の候補となるノードが蓄積され、そこからある評価値


ただし、












このような探索ベースの経路計画において、機械学習を用いたアプローチは主にヒューリスティック関数h の学習とコスト関数c の学習という2種類に大別される。たとえばChoudhuryらの手法1)では、探索時に選択されたノード





一方Vlastelicaら4)は、障害物配置が未知の環境画像からコストマップ
Vlastelicaらのアプローチは経路計画アルゴリズムをブラックボックス関数とみなすことで、ブラックボックス最適化によるコスト関数の学習を実現している。これに対して、我々は経路計画を微分可能な形で陽に書き直すことにより、通常の誤差逆伝播を用いたコスト関数の学習を実現している。このことにより、探索の最終結果のみ活用できるVlastelicaらの手法と異なり、我々の手法は探索の各ステップにおけるノード選択結果に基づいてコスト関数を学習できる。3節ではその詳細について解説する。
2.2 機械学習を活用したサンプリングベース経路計画
サンプリングベース経路計画においては、ロードマップの構築がしばしば手続き全体を律速する。これは、より良い経路を探索するためには環境全体に対して密にサンプルをまく必要がある点、そのサンプル集合からロードマップを構築するために大量の衝突判定が必要である点に起因する。これに対して、もし与えられた問題インスタンスに対して、実際にロードマップ構築をする前に最終的な解経路を予測できれば、その経路周辺を重点的にサンプリングすることにより、より少数のサンプルを用いた効率的なロードマップ構築と経路計画が可能となる。
このような着想のもと、いくつかの研究ではロードマップ構築のためのサンプリングモデル(サンプラー)の学習法が提案されている。たとえば文献5)では条件付き変分オートエンコーダを用いて、環境の障害物レイアウトおよび経路のスタート・ゴール地点を入力として解経路周辺の地点をサンプリング可能なモデルを学習している。このとき、学習されたモデルから得られるサンプルとランダムに抽出されたサンプルを混合してロードマップを構築することで、学習データと異なる環境でモデルからのサンプリングが実際の解経路から外れる場合であっても経路計画が可能となる。ほかにも文献6)では、環境中において多様な経路が共通して通りうる地点を重要な(critical)点と定め、周囲の障害物配置から地点の重要さを推定するモデルを学習している。このようなモデルはいったん学習されると新たな環境の各地点に対する重要度を推定可能であり、推定された重要度に比例した確率で同地点をサンプリングすることで、より少数のサンプルから効率的なロードマップ構築が可能となる。
なお、上記のアプローチでは経路探索に先立ってロードマップの構築が行われるが、環境を逐次的に探索するサンプリングベース経路計画に機械学習を活用する取り組みもある。たとえばMotion Planning Networkと呼ばれる手法7)では、移動エージェントの現在位置とスタート・ゴール地点、障害物の情報を入力として、次ステップで移動すべき地点を直接出力するニューラルネットワークを学習する。そして現在位置からその地点への移動が可能であるか判定し、移動不可能であったときには既存のリプラニングアルゴリズムを用いることで経路を生成する。このようなアプローチは環境全体をカバーするロードマップを構築しないためしばしば効率的に経路計画が可能であるが、得られた経路が最適(あるいは準最適)である保証はない。これに対してNeuralEXTと呼ばれる手法8)では、次ステップでの移動先に加えて、各地点におけるゴールまでの予測経路長(2.2節における

3. Neural A*による経路計画
ここでは、著者らの近年の成果であるNeural A*9)について解説する。Neural A*は2.2節で紹介した探索ベースの経路計画に機械学習を活用するものである。先に紹介した通り、近年の機械学習を活用した経路計画の研究においては、いくつかの関心の高い問題があるが、本研究ではとくに、1)最短経路問題における探索の効率性と最適性のトレードオフの向上、および、2)障害物配置が未知の環境画像(生画像)に対する経路計画、という2つの問題に対して統一的なアプローチを提案する。
以下では、これら2種類の問題に対する提案アプローチの基本的な考え方、Neural A*の学習方法の概要、そしてNeural A*の中核となる微分可能A*の詳細について、順々に説明する。なお、2.2節で紹介した手法と同様、Neural A*は主に格子地図上での経路計画を対象とする。
3.1 ガイドマップを介した経路計画
1つ目の問題である最短経路探索について、実例を用いながらより詳しく説明したい。Neural A*はA*探索アルゴリズムをベースにその探索性能を向上させる手法であるため、まずは通常のA*探索にどのような問題があるのかを見てみる。図2aに示す経路計画の問題インスタンス(即ち、環境マップおよび開始・目標点の組)の例に対して、A*による実際の経路探索の様子を図2bに示す。図2aを人間がみれば、開始・目標点を結ぶ最短経路はおよそ一瞬で見当がつきそうである。しかし、A*探索では手前にあるポケット状の行き止まりで探索が大きく滞留していることがわかる。
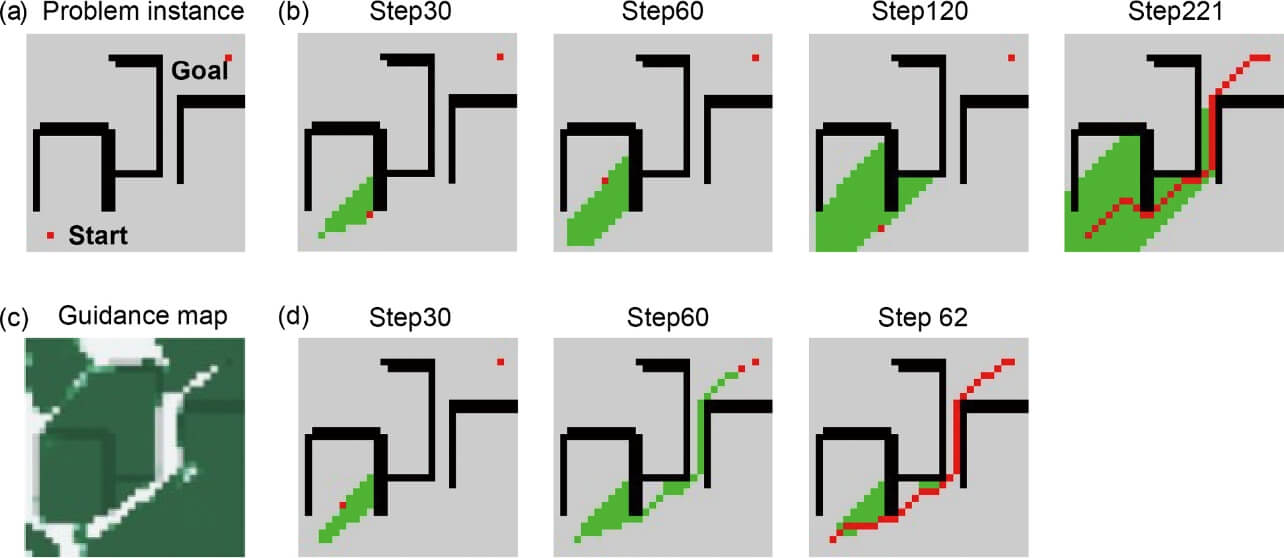
(a)経路計画の問題インスタンスについて、(b)通常のA*探索の動作過程および、(d)Neural A*の動作過程を示す。各マップにおいて、黒は障害物、赤は開始・目標点や探索点、または探索結果を示し、緑は探索済みの領域を表す。Neural A* は問題インスタンスを(d)ガイドマップに変換して探索を行う。ガイドマップ中の白と緑は、優先的に探索すべき低コスト領域および回避すべき高コスト領域を表す。
2つ目の問題である生画像に対する経路計画についても、通常のA*探索が有する問題点と見ることができる。例として、図3aに示すような屋外シーン画像を環境マップとし、マップ中の2点間を結ぶ移動可能な経路の計画問題を考える。図3aの画像を人間が見れば、これが円形状の交差点であり、交差点中心部の領域は通行不可に見えるのでそこを避けた経路を思いつくだろう。実際に、ある歩行者の経路は図3bのようなものであった。しかし、通常のA*探索では、どこにそのような障害物が存在するかのラベル付けがない生画像に対して、このような経路計画を遂行することはできない。

これら2つの問題は一見異なるようであるが、本質的には、環境マップ中の行き止まりや障害物などの視覚的手がかりを探索アルゴリズムが認識・利用できていないという問題として、両者をひと括りに捉えることができる。そこでNeural A*では、それぞれの形式の問題インスタンス(図2aおよび図3a)を畳み込みニューラルネットワーク(以下、エンコーダと呼ぶ)を介してガイドマップ(guidance map)と呼ぶ中間表現(図2cおよび図3c)に変換することで、これら2つの問題に対して統一的なアプローチを可能にする。
ガイドマップは、環境マップ中の各地点v に対してガイドコストと呼ぶ移動コストを割り当てるもので、ここではノードからコストへのマッピング関数
3.2 微分可能A*探索によるガイドマップのEnd-to-end学習
上述のアプローチの課題は、問題インスタンスが適切なガイドマップに変換されるように、どのようにしてエンコーダを学習するかという点である。エンコーダからのガイドマップ出力に対して直接損失を与えて学習する方法も考えられるが、どのような損失を定義すれば経路計画に対して効果的なのかは自明ではない。
この問題に対し我々は、図4に示すような、ガイドマップ変換からA*探索の実行までを包括的に扱うEnd-to-end学習アプローチをとる。即ち、A*アルゴリズムを微分可能な手続きとしてニューラルネットワーク内に組み込むことで、探索結果に対する正解経路との差(損失)の勾配が、誤差逆伝播法により、A*アルゴリズムの一連の探索ステップを介してガイドマップ、そしてエンコーダへと逆伝播可能にする。したがって学習の際には、問題インスタンスと正解経路例の組の集合からなる学習データセットを作成し、この正解経路に探索結果が近づくようエンコーダを学習する。

なお、学習の際の損失関数として、以下のような探索履歴マップC と正解経路マップ

ここで、探索履歴マップ


この損失は、次の2種類のノード選択誤りに対してペナルティを与える。1)false-negativeエラー:本来


3.3 微分可能A*の詳細
Neural A*の中核となる微分可能A*の詳細を解説する。微分可能A*は、順伝搬時においては、2.2節で述べたA*探索の手続き(即ち、Algorithm 1において評価関数に
微分可能A*では、Algorithm 1中の各変数や関数をマップと同じサイズの行列で表し、各演算を行列に対する基本的な演算の組み合わせで表現する。具体的には、開始点












Algorithm 1を微分可能な手続きとして書き直すにあたり、最も重要なステップはノード選択(Algorithm 1の3行目)である。これは評価関数f に対する離散的操作、argminを含むため微分可能ではない。この操作に対して適切な近似勾配を与えるため、評価関数


![V*=Imax[exp(-F/τ)⦿O/<exp(-F/τ),O>]](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-011-fig-03.svg)
ここで関数

選択ノードV *が求まれば、オープンリストO およびクローズドリストC の更新(4行目)は、単純な行列同士の加減算

選択ノードV *の近傍を抽出する工程(5行目)も、一般的な微分可能操作の組み合わせにより、以下のような2値行列で表現できる。

ここで、



その後の近傍ノードのオープンリストへの追加(6行目)も、
これらの処理を目標点が選択されるまで繰り返すと、探索完了となり、それまでに選択されたノードの履歴が2値行列C に蓄積される。C に対して3.3節で述べた損失を計算することで、その勾配を微分可能A*の入力変数であるガイドマップ
3.4 その他の実装の詳細
以上が単一問題インスタンスに対する微分可能A*の基本動作である。実際には、上記内容に加え、学習の効率化や安定化などのための実装上の工夫や詳細があるので、最後にこれらについて軽く補足する。より完全な情報については論文9)を参照されたい。
累積コストの更新 2.2節の説明およびAlgorithm 1では詳細を割愛したが、ノード選択の評価関数f が累積コストg を含む場合、g も探索中に逐次更新する必要がある。これは、基本的には毎回のノード選択後に、その近傍ノード





バッチ学習 ニューラルネットワークの学習においては、複数の入力サンプル{(








これは直感的には、ゴール


エンコーダ設計 エンコーダとなるニューラルネットワークには、セマンティックセグメンテーションなどで用いられるU-Net3)を用い、ガイドマップの出力解像度が入力マップの解像度と同じになるようにした。エンコーダの入力には、X と
一部勾配の無効化 実際の学習では、式(3)のO やG の計算内での一部の変数を計算グラフから切り離して定数として扱うことで、再帰的な逆伝搬の計算チェーンを簡単化し、学習の安定化や消費メモリの削減を行った。
4. 評価実験
本節では、経路探索問題におけるNeural A*の探索性能の評価実験について述べる。
4.1 ベースライン手法
Neural A*の性能評価のため、以下の2つの経路探索手法と比較した。これらはいずれも機械学習を活用した手法で、かつ、内部でNeural A*と同様のA*探索を用いた探索ベースの手法である。
- SAIL1): ヒューリスティック関数を事例データから学習することで高い探索効率を達成した最良優先探索手法。本実験では、学習サンプルを学習したヒューリスティック関数から導く場合(SAIL)と、理想的なオラクルから導く場合(SAIL-SL)の2手法を試した。
- BB-A*4): A*などの組合せ最適化アルゴリズムに対して、ブラックボックス微分と呼ばれる汎用的な近似勾配計算法を適用して学習。この手法は提案手法と似ている面があるが、A*探索を完全なブラックボックスとして扱う点で異なる。
また、非学習型の一般的な探索手法として、最良優先探索(BF)と重み付きA*(WA*)とも比較した。さらに提案手法の変形として、式(3)で累積コストを無視して常に
4.2 評価指標
探索性能の定量的な評価指標として、以下の3つを用いた。
- Opt:手法がどれくらいの頻度で最適(最短)な経路を見つけられたかを0-100(%)の値で表す。
- Exp:通常のA*探索と比べて削減できた探索ステップ数を0-100(%)の値で表す。
- Hmean:OptとExpの調和平均。これは探索の効率と最適性のトレードオフがどれだけ改善したかを示すもので、本研究の主たる評価指標として用いる。
4.3 最短経路問題における性能評価
評価実験では、Motion Planning(MP)11)、Tiled MP、City/Street Map(CSM)12)の3つのデータセットを用いた。MPは32×32サイズの人工的なマップによる経路探索データセットで、Tiled MPではMPのマップをランダムに2×2枚並べて64×64サイズに拡張した。CSMは実際の都市の2値画像マップを64×64サイズに切り出したものである。それぞれ1,000個以上のマップデータを学習用、検証用、テスト用として80%、10%、10%に分割して用いた。
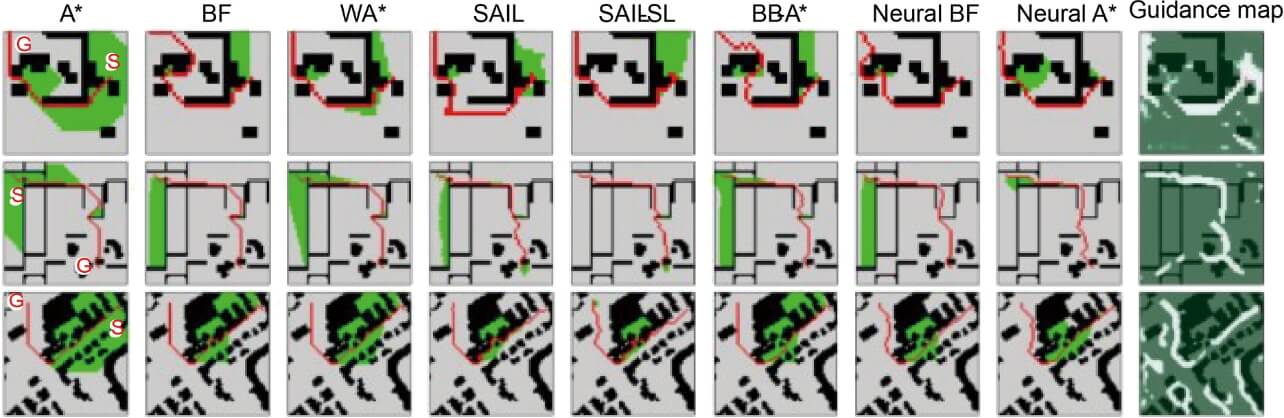
各データセットにおけるOpt、Exp、Hmeanスコアの比較を表1に示す。Neural A*が最も高いHmeanスコアを達成し、探索の効率と最適性のトレードオフ改善効果が最も大きかったことがわかる。MPデータセット中のマップに対する実際の探索結果の例を図5に示す。
| MP Dataset | ||||||
| Opt | Exp | Hmean | ||||
|---|---|---|---|---|---|---|
| BF | 65.8 | (63.8, 68.0) | 44.1 | (42.8, 45.5) | 44.8 | (43.4, 46.3) |
| WA* | 68.4 | (66.5, 70.4) | 35.8 | (34.5, 37.1) | 40.4 | (39.0, 41.8) |
| SAIL | 34.6 | (32.1, 37.0) | 48.6 | (47.2, 50.2) | 26.3 | (24.6, 28.0) |
| SAIL-SL | 37.2 | (34.8, 39.5) | 46.3 | (44.8, 47.8) | 28.3 | (26.6, 29.9) |
| BB-A* | 62.7 | (60.6, 64.9) | 42.0 | (40.6, 43.4) | 42.1 | (40.5, 43.6) |
| Neural BF | 75.5 | (73.8, 77.1) | 45.9 | (44.6, 47.2) | 52.0 | (50.7, 53.4) |
| Neural A* | 87.7 | (86.6, 88.9) | 40.1 | (38.9, 41.3) | 52.0 | (50.7, 53.3) |
| Tile MP Dataset | ||||||
| Opt | Exp | Hmean | ||||
|---|---|---|---|---|---|---|
| BF | 32.3 | (30.0, 34.6) | 58.9 | (57.1, 60.8) | 34.0 | (32.1, 36.0) |
| WA* | 35.3 | (32.9, 37.7) | 52.6 | (50.8, 54.5) | 34.3 | (32.5, 36.1) |
| SAIL | 5.3 | (4.3, 6.1) | 58.4 | (56.6, 60.3) | 7.5 | (6.3, 8.6) |
| SAIL-SL | 6.6 | (5.6, 7.6) | 54.6 | (52.7, 56.5) | 9.1 | (7.9, 10.3) |
| BB-A* | 31.2 | (28.8, 33.5) | 52.0 | (50.2, 53.9) | 31.1 | (29.2, 33.0) |
| Neural BF | 43.7 | (41.4, 46.1) | 61.5 | (59.7, 63.3) | 44.4 | (42.5, 46.2) |
| Neural A* | 63.0 | (60.7, 65.2) | 55.8 | (54.1, 57.5) | 54.2 | (52.6, 55.8) |
| CSM Dataset | ||||||
| Opt | Exp | Hmean | ||||
|---|---|---|---|---|---|---|
| BF | 54.4 | (51.8, 57.0) | 39.9 | (37.6, 42.2) | 35.7 | (33.9, 37.6) |
| WA* | 55.7 | (53.1, 58.3) | 37.1 | (34.8, 39.3) | 34.4 | (32.6, 36.3) |
| SAIL | 20.6 | (18.6, 22.6) | 41.0 | (38.8, 43.3) | 18.3 | (16.7, 19.9) |
| SAIL-SL | 21.4 | (19.4, 23.3) | 39.3 | (37.1, 41.6) | 17.6 | (16.1, 19.1) |
| BB-A* | 54.4 | (51.8, 57.1) | 40.0 | (37.7, 42.3) | 35.6 | (33.8, 37.4) |
| Neural BF | 60.9 | (58.5, 63.3) | 42.1 | (39.8, 44.3) | 40.6 | (38.7, 42.6) |
| Neural A* | 73.5 | (71.5, 75.5) | 37.6 | (35.5, 39.7) | 43.6 | (41.7, 45.5) |
5. 生画像マップに対する経路計画
障害物位置のラベル付けがない生画像マップに対する経路計画問題について、Neural A*とBB-A*の性能比較実験を行った。実験では、Stanford Drone(SD)データセット13)に含まれる屋外シーンの歩行者軌跡データを用いて、歩行者の経路予測問題のデータセットを作成した。そして、シーン画像と開始・目標点が与えられた際に、各手法がどれだけ正確に実際の歩行者経路を予測できるか評価した。
表2では予測経路と正解経路の間のchamfer距離を比較している。Intra-scenesでは、学習データとテストデータに同じ撮影場所の画像を用いることで、未知の歩行者に対する予測精度を測る。Inter-scenesでは、学習データとテストデータで異なる撮影場所の画像を用いるleave-one-out交差検定を行い、未知の場所に対する汎化性能を測る。どちらの場合においてもNeural A*が、より正解に近い経路を予測していることがわかる。
| Intra-scenes | Inter-scenes | |
|---|---|---|
| BB-A* | 152.2(144.9, 159.1) | 134.3(132.1, 136.4) |
| Neural A* | 16.1( 13.2, 18.8) | 37.4( 35.8, 39.0) |
実際の結果の例を図6に示す。最初2つの例では、Neural A*が定性的にも正解に近い経路を予測していることがわかる。一方、3つ目の例では、開始・目標点の間に複数の妥当な経路があるため、予測に失敗している。このような場合に対する拡張として、複数の経路例を確率的にサンプリングできるようにする生成的アプローチ14)などが考えられる。

6. むすび
本論文では、「機械学習を活用した経路計画手法」と題して、この分野における最新の研究動向および、我々の研究成果であるNeural A*について解説した。同分野は様々な問題意識のもと研究がされているが、そのなかでも、経路探索の最適性と効率性のトレードオフ向上と、障害物位置を未知とした生画像マップに対する経路計画という2つの問題に対して、Neural A*は統一的な解決アプローチを提案した。評価実験では、従来の機械学習を用いない経路探索アルゴリズムと比べ、Neural A*は探索の最適性を大きく損なうことなく効率性を飛躍的に向上できることが確かめられた。また、固定カメラ画像に対する歩行者の経路予測問題では、実際の歩行者の移動経路を従来手法より正確に予測できることが確かめられた。同技術は、ロボットマニピュレータの高次元状態空間における動作計画をはじめ、様々なシーンへの適用が期待される。
参考文献
- 1)
- Choudhury, S.; Bhardwaj, M.; Arora, S.; Kapoor, A.; Ranade, G.; Scherer, S.; Dey, D. Data-driven planning via imitation learning. International Journal of Robotics Research (IJRR). 2018, Vol.37, No.13-14, p.1632-1672.
- 2)
- Takahashi, T.; Sun, H.; Tian, D.; Wang, Y. “Learning heuristic functions for mobile robot path planning using deep neural networks”. Proceedings of the International Conference on Automated Planning and Scheduling (ICAPS). 2019, p.764-772.
- 3)
- Ronneberger, O.; Fischer, P.; Brox, T. “U-net: Convolutional networks for biomedical image segmentation”. Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). 2015, p.234-241.
- 4)
- Vlastelica, M.; Paulus, A.; Musil, V.; Martius, G.; Rolinek, M. “Differentiation of blackbox combinatorial solvers”. Proceedings of the International Conference on Learning Representations (ICLR). 2020, p.1-19.
- 5)
- Ichter, B.; Harrison, J.; Pavone, M. “Learning sampling distributions for robot motion planning”. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). 2018, p.7087-7094.
- 6)
- Ichter, B.; Schmerling, E.; Lee, T. W. E.; Faust, A. “Learned critical probabilistic roadmaps for robotic motion planning”. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). 2020, p.9535- 9541.
- 7)
- Qureshi, A. H.; Simeonov, A.; Bency, M. J.; Yip, M. C. “Motion planning networks”. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). 2019, p.2118-2124.
- 8)
- Chen, B.; Dai, B.; Lin, Q.; Ye, G.; Liu, H.; Song, L. “Learning to plan in high dimensions via neural exploration-exploitation trees”. Proceedings of the International Conference on Learning Representations (ICLR). 2020, p.1-15.
- 9)
- Yonetani, R.; Taniai, T.; Barekatain, M.; Nishimura, M.; Kanezaki, A. “Path planning using neural A* search”. Proceedings of International Conference on Machine Learning (ICML). 2021, p.12029-12039.
- 10)
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. “Binarized neural networks”. Proceedings of the Advances in Neural Information Processing Systems(NeurIPS). 2016, p.4107-4115.
- 11)
- Bhardwaj, M.; Choudhury, S.; Scherer, S. “Learning heuristic search via imitation”. Proceedings of the Conference on Robot Learning (CoRL). 2017, p.271-280.
- 12)
- Sturtevant, N. Benchmarks for grid-based pathfinding. IEEE Transactions on Computational Intelligence and AI in Game. 2012, Vol.4, No.2, p.144-148.
- 13)
- Robicquet, A.; Sadeghian, A.; Alahi, A.; Savarese, S. “Learning social etiquette: Human trajectory understanding in crowded scenes”. Proceedings of the European Conference on Computer Vision (ECCV). 2016, p.549-565.
- 14)
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. “Trajectron++: Multi-agent generative trajectory forecasting with heterogeneous data”. Proceedings of the European Conference on Computer Vision (ECCV). 2020, p.1-17.
本文に掲載の商品の名称は、各社が商標としている場合があります。



















