雑踏の中で動き回る自律走行ロボット~社会ジレンマを解決する強化学習の活用
私たちの日常にロボットが進出するにつれ、人が介在する環境下におけるロボットナビゲーション技術はますます重要なものとなってきている。我々人間は混雑した駅構内やショッピングモールなど様々な場所、状況において社会規範を守りながら目的地に到達するために高度な意思決定を行っているが、同等の能力をロボットで実現することは容易ではない。人が介在する環境でのロボットナビゲーションでは安全性と効率性2つの側面で問題を捉える必要があり、この両者はトレードオフの関係にあるためである。本稿では、混雑環境下におけるナビゲーションの主なアプローチを俯瞰すると共に、我々が公共空間で暗黙のうちに意識している社会規範のモデルとして社会ジレンマに着想を得たナビゲーション手法について解説する。
1. まえがき
物流、病院、ショッピングモール、そして駅構内での案内に至るまで、我々の日常さまざまな場面で移動ロボットが導入され始めている。それに伴い、ヒューマンセントリックな環境下におけるロボットナビゲーション技術はますます重要なものとなっているといえよう。
ロボットナビゲーションでは環境マップ中において障害物を回避しながら目的地へ至る経路の計画を行うが、混雑環境下における経路計画は未だ困難な課題である。第一に人が介在する環境では環境マップが刻一刻と変化するため、取るべき経路を事前に計画しておくというアプローチは取れず、環境の変化に合わせて計画を逐次更新していく必要がある。更に、公共空間、特に人が介在する環境下において、社会規範を意識した振る舞いを(我々人間が自然とそうしているように)ロボットに行わせることは極めて難しい。より具体的には我々は雑踏の中を歩く際、周辺歩行者との衝突回避だけでなく目的地へ効率的にたどり着けるよう、つまり安全性と効率性のトレードオフを意識しながら非常に高度な意思決定を適応的に行なっているが、これと同等の機能をロボットで実現する必要がある。そこで本稿では、「人が介在する環境下における適応的なナビゲーションをどう実現するか?」及び「社会規範をロボットにどう認識させるべきか」という2つの技術課題について解説する。
動的な環境下におけるナビゲーションにおいて、従来では予測と計画を別々に取り扱うアプローチが取られてきた1,2)。まず環境マップの変化を予測し、その予測結果をもとに安全なナビゲーションを行うというものである。一方、これらの2段階に分かれたナビゲーションに対し、適応的に環境の予測と取り得る行動の決定を強化学習によって同時に行う手法が研究されている4-6)。しかしながら、いずれのアプローチも環境の複雑さが増加するほど、つまり多数の動的オブジェクトで囲まれた混雑環境下では Freezing Robot Problem7,8)と呼ばれる問題に陥ることが知られている。Freezing Robot Problemとは、周辺環境がある混雑度に到達すると、ロボットは安全な経路を導き出すことができず停止(Collision)してしまうか、不必要な迂回路を取ることにより目的地への到達が大幅に遅れてしまう状態(Timeout)を指す(図1左)。周囲に十分な走行可能領域がない限り迂回路を取り続けることはできず、また搭載されているバッテリー容量も有限であるため、結果としてロボットは高い確率で目的地へ到達することができなくなってしまう。我々人間はなぜ極めて混雑した状況でもこの問題に陥らず確実に目的地へ辿り着くことができるのだろうか?そこで、移動ロボットによる経路計画とは異なり、人間は衝突を回避して迂回路を取るほか、環境に介入して自ら経路を作り出すことができるという点に着目した。この環境への介入行動をロボットに模倣させることを考える。
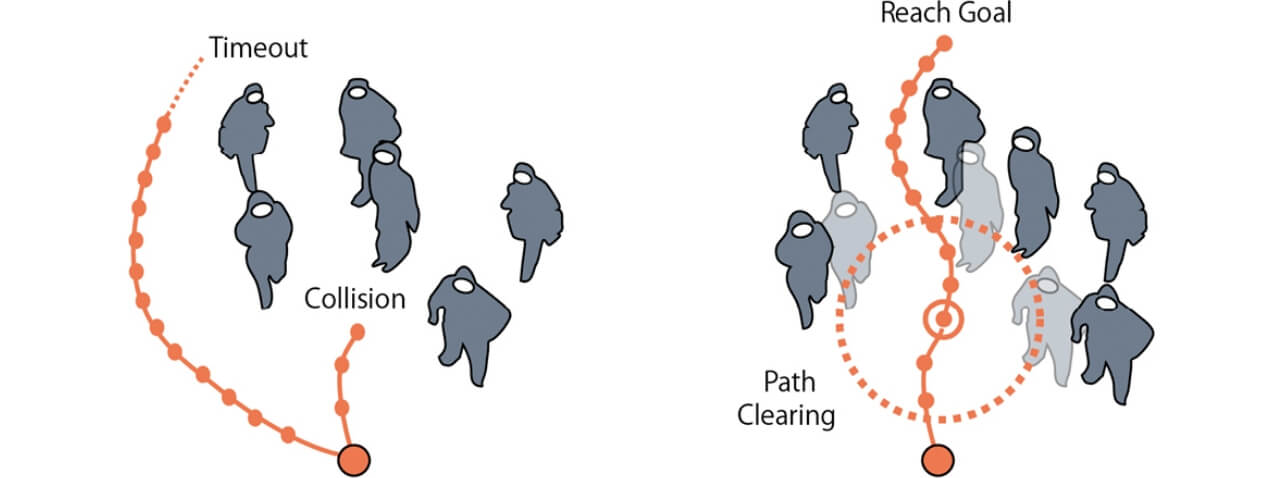
右)介入行動によって、確実に目的地へ到達することができる。
図1 Freezing Robot Problem
まずロボットが行うことができる環境への介入行動を以下のように定義する。従来のナビゲーションではロボットが取れる行動として移動及び衝突回避のみが想定されていたが、更に自動車のクラクションのように警告音を鳴らして介入することができるとする。つまり、環境介入によって目的地へ至る経路を自ら作り出す(Path Clearing)能力を持たせるとする(図1右)。このようにロボットが取り得る行動パタンの拡張によって、完全にロボットが停止してしまう状態(図1左)から脱し、確実に目的地へ到達する確率を高めることができると考えられる。しかし、この介入行動の実装には「この環境への介入どのような判断基準及び頻度で行うべきか」という新たな問題が伴う。
ロボットが環境に介入する機構については、古くから提示、誘導光を用いる方法9)、警告音を用いる方法10)が提案されてきた。しかしながら、環境介入は歩行者が接近した際の局所的な判断によってのみ行われ、介入による環境への長期的な影響はこれまで議論されてこなかった。十分な走行可能領域が確保できないような混雑環境下においては、環境介入を頻繁に行うことが安全かつ効率的な経路計画に繋がるわけではない。何故ならば、環境に頻繁に介入すると自然な人の流れを阻害してしまい、結果として目的地への到達が遅れてしまうからである。また逆に、衝突を避け迂回路をとりすぎると目的地への到達が遅れてしまう。つまり、能動的に介入行動を駆使しながら目的地へ効率的に辿り着こうとすること、消極的に周辺の歩行者にぶつからないよう安全性に配慮した経路を選択すること、この効率性と安全性はトレードオフの関係にある。このトレードオフをどのように調節して環境への介入タイミングを制御するかが介入行動を伴うナビゲーションの主要な技術課題となる。
本稿では、この衝突回避と環境への介入頻度の制御を社会ジレンマの問題として捉えることを考える。社会ジレンマとは、個人と全体が資源を共有している状況において、個人にとって合理的な選択が必ずしも社会全体の利益と一致しない葛藤(ジレンマ)がある状態を指す。つまり、個人にとって最適な行動が必ずしも社会全体にとって最適な行動とならないということである。経済学の分野で有名な共有地の悲劇11)を例に挙げる。まず複数の酪農家が共有地である牧草地に牛を放牧するとする。個々の酪農家としては放牧するほどに牛を肥やすことができ短期的には恩恵を受けられるが、全ての酪農家が同様に牛を放牧すると共有資源である牧草の枯渇が起こり、長期的には全体の利益を損ねることになる。このような社会ジレンマは牧草地における過放牧のほか、環境汚染や乱獲、無線通信のリソース制御など我々の身近な社会の中で当て嵌まる例が非常に多くある。
ロボットナビゲーションの例を前述の社会ジレンマの枠組みで捉えてみると、公共空間における限られた走行可能領域を複数の周辺歩行者と移動ロボットが共有し、毎時取り得る経路を分け合っている状況であると考えられる。ここでの個人の利益とは目的地に可能な限り早く到達する状態に対応し、個人の利益を追求し頻繁に環境への介入を行うことにより、自然な人の流れを阻害し自身も含めた全体の目的地への到達を阻害する状態が全体の利益を損ねることに対応するであろう。この着想を元に、本稿では我々の提案する環境介入を含む適応的なロボットナビゲーションを、社会ジレンマを伴う意思決定問題としてモデル化し、深層強化学習によって最適な行動方策を獲得する手法L2B(Learning to Balance)について解説する。
2. 関連研究
2.1 混雑環境下におけるロボットナビゲーション
混雑環境下におけるナビゲーションでは、まず群衆の自然な衝突回避行動を模倣するアプローチが考えられてきた。一般に広く用いられるモデルとしてRVO(reciprocal velocity obstacles)及びその拡張手法であるORCA(optimal reciprocal collision avoidance)1)があり、これらはVelocity Obstaclesとして定義される衝突範囲を利用した衝突回避手法の安定な拡張手法として広く利用されている。また実際の人流の振る舞いと類似する動きを学習する模倣学習を用いる方法もある16)。更に、近年深層強化学習によって衝突回避と経路計画を同時に行う方法が提案され、混雑環境下におけるロボットナビゲーションにおいて優れた成果を上げてきた4-6)。
ここではまず、ロボットナビゲーションを強化学習の問題として解く基本的なアプローチについて解説する。混雑環境下における経路計画は各時刻で障害物を避けながら目的地へ到達するためのロボットの進行方向及び速度を決定する、連続的な意思決定問題と捉えることができる。この連続的な意思決定はマルコフ決定過程(Markov Decision Process, MDP)によってモデル化することができる。その概念図を図2に示す。MDPでは環境(Environment)から状態(State)が行動主体(Agent)から観測可能であるとし、エージェントが方策π(st , at )に基づいて最適な行動(Action)を選択するとことにより環境が次のステップへ遷移し、エージェントは報酬関数に基づいて報酬rt =R(st , at )を得る。
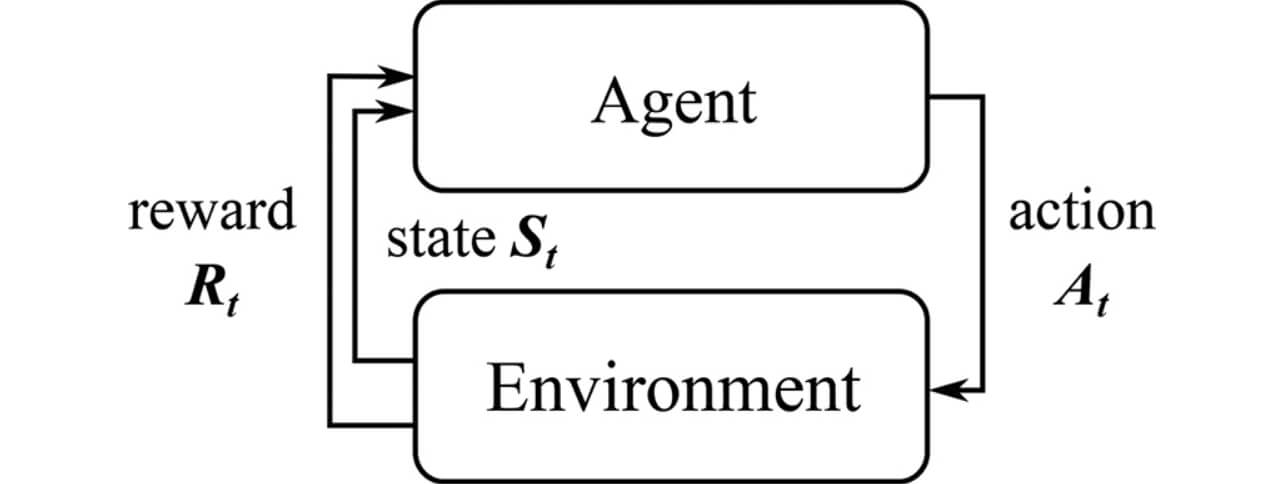
混雑環境下のナビゲーションにおいて状態st はロボット及び周辺歩行者の状態によって構成されるが、移動ロボット自体の状態は完全に観測可能である一方で、目的地情報を含む周辺歩行者の状態については、外部から観測可能な速度情報等の情報のみ観測可能(部分観測可能)であるとする。つまり、部分観測マルコフ決定過程(Partially Observable Markov Decision Process, POMDP)としてロボットナビゲーションの問題を定式化することになる。強化学習ではこのような枠組みの中で観測と行動を繰り返しながら累積報酬を最大化するような最適方策π*を学習で獲得することを目的とする。
深層強化学習を複数ロボットの衝突回避制御に先駆的に取り入れたCADRL(Collision Avoidance with Deep Reinforcement Learning)4)では、2エージェント間の衝突に関するペナルティを報酬関数に組み込み、獲得した方策を各エージェントで独立に実行させることで、中央集権的な制御を必要としない衝突回避手法を実現した。CADRLはロボット同士の衝突回避において優れた性能を示したが、歩行者による混雑環境下においては歩行者同士、及び歩行者―ロボット間の複雑なインタラクションを十分に考慮できていないために積極的に危険な経路を取ってしまうケースが散見された。これに対し、後続研究である SARL12)では、強化学習における価値関数を表現するネットワークに周辺歩行者のインタラクションをエンコードするモジュールを組み込むことで、より安全な経路を確実に選択することができるナビゲーション手法を提案した。
しかしながら、これらのアプローチは周辺環境が5名以下といった比較的混雑していない環境を対象としているほか、周辺歩行者に対する衝突回避のみに重点がおかれている。環境がある混雑度に達するとプランナは全てのパスが走行不能と判断してしまい、ロボットは完全に停止してしまうか衝突を回避するため不必要な迂回路をとってしまう。深層強化学習を始めとしたこれらの手法はいずれも、Freezing Robot Problemを完全には解決できない。我々のアプローチは、衝突回避だけでなく能動的に群衆に働きかけ経路を作り出すことができる方策を学習によって獲得することにより、ロボットが停止せず確実に目的地へ辿り着くようにするものである。
2.2 社会規範のモデル化
周囲の歩行者と適切にインタラクションを取るには社会規範を意識する必要があり、ロボットナビゲーションの文脈においても社会規範の学習が盛んに研究されてきた。群衆の自然な流れから社会規範に従うルールを学習し、その枠組みをロボットナビゲーションに応用する試みもある14,15)。また別のアプローチでは歩行者の社会規範を表現する方法としてゲーム理論に影響を受けたモデルが提案されている3)が、中でも興味深いのはマルチエージェントシミュレーションの分野で提案された Sequential Social Dilemmas (SSD)13)である。
まずゲーム理論について概説するが、単目的最適化や多目的最適化は全体合理性を追求する目的関数が設定されている一方で、「ゲーム」は個々の行動主体の合理性、つまり個々のエージェントが他者とは独立に自己の目的関数を最大化することを前提とした最適化問題である。ゲーム的状況とは、環境に複数の意思決定主体または行動主体が存在し、それぞれが個別の目的関数の最適化を目指して相互に依存している状況を意味する。ゲーム的状況の中で行動主体がどのような意思決定をするのかを数理モデルによって表現し、分析手法を理論化したものがゲーム理論である。
社会におけるさまざまなゲーム的状況の中で、特に我々の身近に存在する問題としては共有地の悲劇や囚人のジレンマに代表される社会的ジレンマがある。社会的ジレンマとは、個人と全体が資源を共有している状況において、個人にとって合理的な選択が必ずしも社会全体の利益と一致しない葛藤(ジレンマ)がある状態を指す。表1に社会的ジレンマがある状況において、エージェントA、Bがそれぞれ協力(πc )・非協力(πd )行動を選択した際にエージェントAが受け取る利得構造を示す。
| 協力(πc ) | 非協力(πd ) | |
| 協力(πc ) | R 相互協力 | S 他方に裏切られる |
| 非協力(πd ) | T 自身が裏切る | P 両者が裏切る |
この利得行列(Pay-off Matrix)を持つマトリックスゲームが以下の条件を満たすケースが社会的ジレンマである。
- R>P : 相互協力が相互敵対より利得が高い
- R>S: 相互協力が一方に裏切られるよりも利得が高い
- 2R>T+S : 相互協力が全体的に最も利得が高い
- T>R : 相手を裏切る方が相互協力よりも利得が高い
- またはP>S : 相互に裏切る方が一方的に裏切られるよりも利得が高い(罰則が軽い)
しかしながら、実世界の問題では時間軸が存在し、エージェントの行動空間に対し協調・非強調は二値で常に分離可能ではなく、段階的な量である。また、エージェントは他エージェントの状態を完全に観測することはできず、部分的な観測のみで意思決定を行う必要がある。これらを考慮し、従来のMatrix Game Social Dilemma(MGSD)を時間軸に拡張し、POMDPとして扱えるようにした枠組みがSequential Social Dilemmas(SSD)である。
時間軸での状態遷移を伴うマルコフゲームは、状態空間S 、行動空間A1, A2、状態遷移関数T、報酬関数R ∈S ×A1×A2から構成される。各エージェントの行動はそれぞれ独立に決定される一方で、報酬は状態とエージェントの行動でなく、自己と他者両方の行動に依存する。SSDはこのマルコフゲームにおける報酬構造に対し、上述の社会的ジレンマの制約を課したものである。本稿では、混雑環境下におけるロボットナビゲーションを社会ジレンマを伴うマルコフゲームである、SSDに類似した状況であるということに着想を得、強化学習によって最適な方策を獲得する方法について解説する。
3. 強化学習を用いたナビゲーション
介入行動を伴うロボットナビゲーションをPOMDPとして定式化を行う。ここで、ロボットと群衆(周辺歩行者のグループ)をそれぞれロボットエージェントと群衆エージェント 2つのタイプのエージェントとして取り扱い、独立した異なる行動方策を持っているものとする。特に、今回はロボットと個々の周辺歩行者ではなく、ロボットと群衆全体との間での意思決定に伴う社会的ジレンマを扱うため、群衆エージェントは複数の歩行者を1つのエージェントとして簡易的に取り扱い、ロボットエージェントから未知の方策に従っているものとする。
各タイムステップt において、群衆エージェントの状態s は部分的に観測可能であり、目的地の情報は外部からは観測不可能であるとする。群衆エージェントの状態がs ={so , sh }のように観測可能(Observable)な状態so と観測不能(hidden)な状態sh から構成されているとすると、ロボットエージェントから観測できる状態は自身の状態と群衆エージェントの部分観測を含め

![st=[dt(g),vt,vpref,r(c),r(b)]sto~=[Pt~,vt~,dt~,r~]](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-005-fig-01.svg)
ここで、d(g )は目的地までの距離、vt ,vpref はそれぞれ現在速度及び理想とする速度、r(c )、r(b )は衝突を考慮する半径及び介入行動によって周辺歩行者が影響を受ける距離半径である。強化学習では、累積報酬の期待値を最大化するような最適な方策

また、累積報酬の期待値をエンコードする最適な価値観数V * は以下の式で表される。
![V*(stjn)=E[∑t'=tTγt'・vprefR(stjn,π*(st'jn))],](/jp/ja/assets/img/technology/omrontechnics/20211119/20211119-053-2-005-fig-03.svg)
ここで、γ ∈ [0,1)は割引率であり、エージェントの現在速度によって割引率が増減しないようタイムステップ及び理想とされる速度vpref によって正規化されている。高次元の状態空間を扱うため、価値関数をSARL12)に準拠したニューラルネットワークで近似することとする。また、学習するのはロボットエージェントの方策π のみであり、群衆エージェントの方策π としてはルールベースの衝突回避手法であるORCA1)を用いる。
4. 社会的ジレンマを考慮した報酬設計
本研究では群衆への介入行動を伴うロボットナビゲーションを社会ジレンマを伴う意思決定問題として捉える。Sequential Social Dilemmas (SSD)では、個々のエージェントの行動によって毎時状況が遷移するマルコフゲームにおいて、個人と全体が資源を共有している状況において、個人にとって合理的な選択が必ずしも社会全体の利益と一致しない葛藤(ジレンマ)がある状態を指す。ロボットナビゲーションの文脈における個人の利益とは目的地に可能な限り早く到達することであるとすると、個人の利益を追求し頻繁に環境への介入を行うことは自然な人の流れを阻害し自分も含めた全体の目的地への到達を阻害するため、自身を含む全体の長期的な利益を損ねることに対応する。πc ,πd をそれぞれ協調的、非協調的方策であるとすると、SSDの枠組みにおいて、R、P、S、Tそれぞれの利得を強化学習の報酬として設計することを考える。ここで、前章で解説した通りRは相互協力、Sは自分のみが協力、Tは相手のみが協力、Pは双方とも協調しなかった場合の利得である。
相互協力による報酬 R =V (πc ,πc )をロボットと群衆がそれぞれ衝突回避し道を譲り合う状態、S =V(πc ,πd )を群衆の経路を優先してロボットが迂回路を取るケースであるとする。T =V(πd ,πc )はは介入動作や自己経路優先により群衆の通行をロボットが阻害するケースであり、P =V(πd ,πd )はロボット、群衆が両者とも自己経路を優先し、渋滞或いは衝突してしまうケースと考える。また、各エピソードは目的地に到達、周辺歩行者に衝突、所定の所要時間を超過する何れかの条件を満たすとその結果に紐づく報酬を得て終了するものとする。
以上を踏まえて社会ジレンマを考慮した報酬関数の設計を行う。環境から得られる報酬Re 及び群衆エージェントの行動と自己の行動の組み合わせによって得られる報酬をRs とすると、報酬関数R(st , at )を以下のように表すことができる。

Re は一般的な衝突回避に関する報酬である。ただし、ロボットエージェントの現在位置pt が目的地p(g )に到達すると得られる成功報酬は、所定時間に対する所要時間の割合とその係数α に応じて減衰するものとする。また、周辺歩行者との最短距離dt が衝突判定距離dmin を下回ると衝突とみなし、それ以外の状態については報酬が発生しないものとする。エージェントが目的地に到達または衝突するとエピソードは終了する。

一方、周辺エージェントとのインタラクションにより発生する社会的な報酬Rs は介入行動及び接近行動によって生じるペナルティによって形成される。2値符号である



ここで、α、β、γ はそれぞれ目的地へ早く到達したいとする積極性の制御項、積極的な介入行動によって生じるペナルティの重み、消極的に衝突を避けようとする傾向の調整項である。提案法では、このような社会ジレンマを考慮した報酬系の上で累積報酬の期待値を最大化することにより、安全性と効率性のトレードオフを調停(L2B: Learning to Balance)することを目指す。
5. 実験
社会ジレンマを考慮した提案フレームワークL2Bの効果を検証するため、群衆環境を模したシミュレーションにおいて提案手法の有効性の評価を行なった。
5.1 シミュレーション
前章までで述べたように混雑環境を対象とした既存研究は衝突回避のみを扱っているため、介入行動を伴うナビゲーションの評価環境は存在しない。そこで、脅威に対して人の回避行動が距離に応じてどう変化するかをRVOの拡張として取り入れたERVO(Emotional Reciprocal Velocity Obstacles)を模したシミュレーションシステムを実装し、介入行動に対する人の反応をERVOにより生成することとした。図3に示すように、ロボットエージェントが半径r(b)を影響半径とする警告音で介入行動を選択した際、その距離r(b)に応じて影響半径から退避する回避行動を取るものとする。また、群衆が目的地へ向かう際の動きは同様にRVOの拡張であるORCAに従うものとする。4.0[m2]の空間に歩行者人数N ={5,10,15,20}複数の混雑度のシナリオを作成し、各混雑度における提案法の効果を確認した。
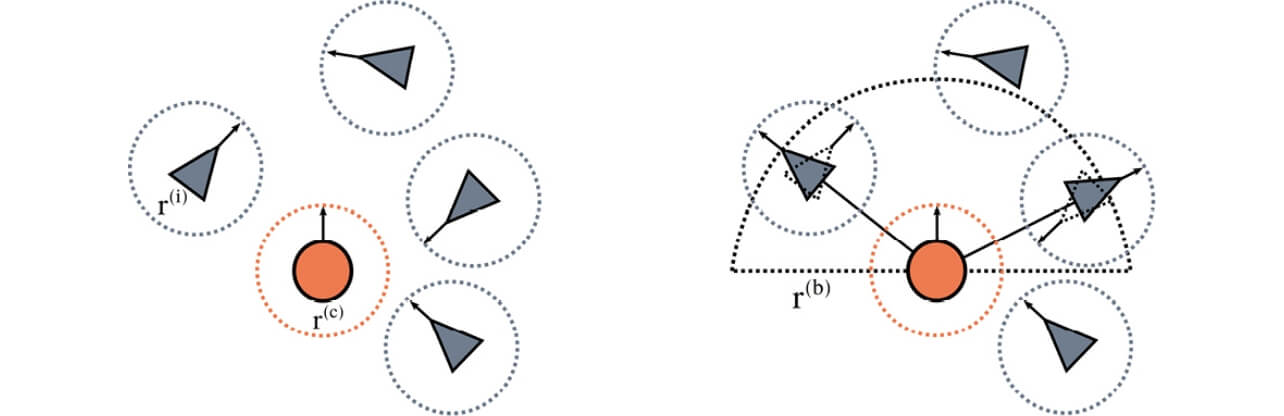
図3 ERVOを元にした介入行動に対するシミュレーション
5.2 評価方法
混雑度に応じて円周上にランダムにエージェントを配置し、対岸の目的値にお互い交差しながら進行するシナリオ(Circle Crossing Scenario)をベンチマークとして用いる。エージェントの配置には正規分布に従うランダムノイズを加えて500回のテストケースを作成し、フォーマンスを目的地までの到達率(Success)、衝突率(Collision)、目標時間内に目的地に到達せずタイムアウトした割合(Timeout)、目的値までの平均所要時間(Time)4つのメトリクスで評価を行なった。比較手法として、介入方策を学習によって獲得する手法はこれまで存在していないため、SARLのモデルをベースに介入行動を導入した提案法を今回L2B-SARLと呼称するものとし、介入方策を用いないオリジナルのSARLを各混雑度のシナリオに適用した結果と比較を行った。
表2に各メトリクスでの評価結果を示す。SARLはより混雑した環境下では到達率が下がってしまう結果となった。これは介入方策を持たないオリジナルのSARLでは消極的に衝突回避を行うことしかできないので、迂回路を取りすぎてタイムアウトになるケースが頻繁に起こるためである。一方、L2B-SARLはN>15の混雑した環境においてもタイムアウト率が非常に低い結果となっており、目的地へ確実に到達できていることがわかる。また、環境への介入は常により効率的に目的地へ到達する結果には至らず、状況によっては介入を用いない方策よりも目的地への到着が遅れるケースが散見された。これは前章で述べたように環境介入は群衆の動きを乱すことにより、多用することによって自己及び全体に不利益をもたらす効果があるという仮説と一致している。
| Methods | N | Success | Collision | Timeout | Time |
|---|---|---|---|---|---|
| L2B-SARL | 20 | 0.906 | 0.094 | 0.000 | 13.85 |
| SARL [12] | 0.700 | 0.184 | 0.116 | 13.50 | |
| L2B-SARL | 15 | 0.880 | 0.118 | 0.002 | 11.60 |
| SARL [12] | 0.778 | 0.064 | 0.158 | 12.43 | |
| L2B-SARL | 10 | 0.904 | 0.086 | 0.004 | 11.31 |
| SARL [12] | 0.922 | 0.046 | 0.032 | 11.91 | |
| L2B-SARL | 5 | 0.978 | 0.020 | 0.002 | 10.14 |
| SARL [12] | 0.966 | 0.032 | 0.002 | 10.09 | |
| L2B-SARL | average | 0.917 | 0.079 | 0.002 | 11.72 |
| SARL [12] | 0.841 | 0.081 | 0.077 | 11.98 |
更に、図4に定性的な評価結果を示す。橙マーカがロボットエージェントが取った軌跡及び介入行動を選択した地点、灰マーカが群衆エージェント介入方策を用いた上段(提案法)では、衝突回避方策のみの下段(SARL)よりも迂回路に偏らず効率的な経路を選択でき、かつ適切な頻度で介入行動を行えていることが確認できた。
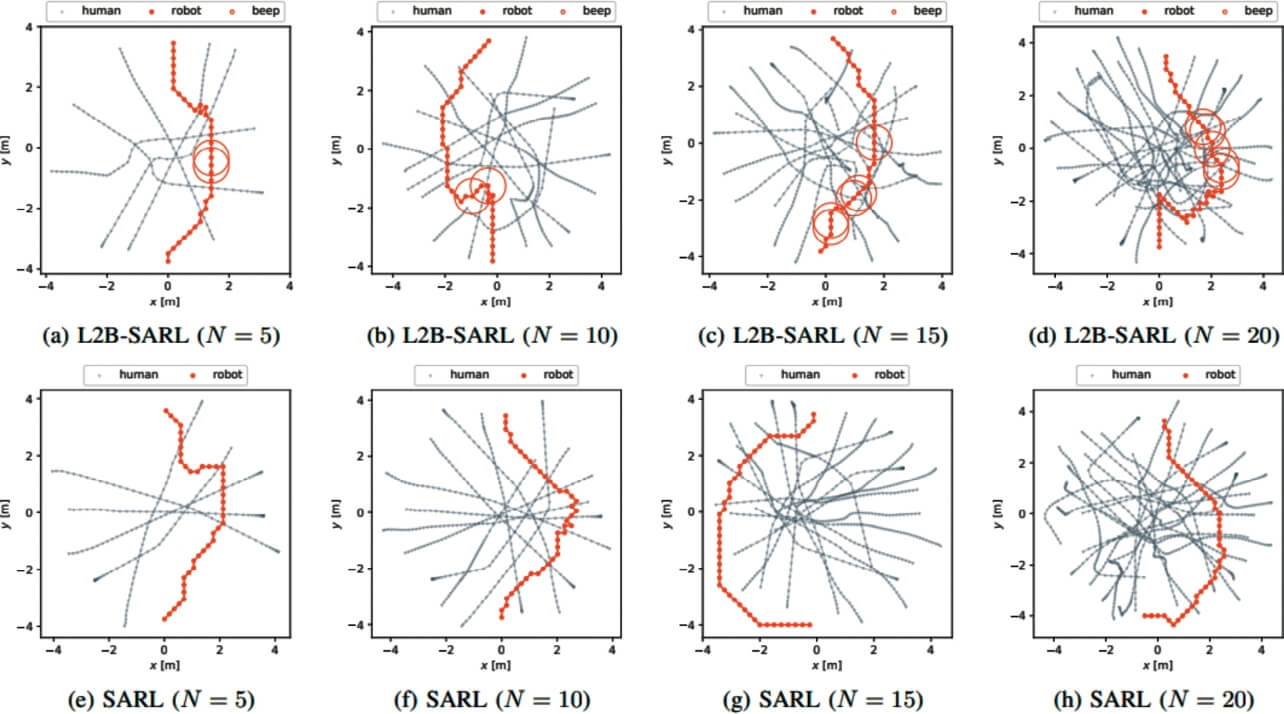
※クリックすると別ウインドウが開きます
6. むすび
本稿では、適応的なロボットナビゲーションの枠組み及び混雑環境下における課題を紹介し、介入行動を伴う新たなナビゲーション技術の枠組みについて解説した。現状はシミュレーション環境のみでの評価のみであるが、提案法は Non-Holonomic なロボットのキネマティクスにも対応することができるため、移動ロボット実機で訓練した方策を利用することも可能である。今回は単一エージェントのみを学習対象としたが、社会ジレンマの介在する環境下において、マルチエージェント強化学習の枠組みにより複数ロボットの協調行動を引き出すような発展も考えられる。
参考文献
- 1)
- Van Den Berg, J.; Guy, S. J.; Lin, M.; Manocha, D. “Reciprocal n-body collision avoidance”. Robotics Research. Springer, 2011, p.3-19.
- 2)
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robotics & Automation Magazine. 1997, Vol.4, No.1, p.23-33.
- 3)
- Fisac, J. F.; Bronstein, E.; Stefansson, E.; Sadigh, D.; Sastry, S. S.; Dragan, A. D. “Hierarchical game-theoretic planning for autonomous vehicles”. IEEE International Conference on Robotics and Automation. 2019, p.9590-9596.
- 4)
- Chen, Y. F.; Liu, M.; Everett, M.; How, J. P. “Decentralized noncommunicating multiagent collision avoidance with deep reinforcement learning”. IEEE International Conference on Robotics and Automation. 2017, p.285-292.
- 5)
- Chen, Y. F.; Everett, M.; Liu, M.; How, J. P. “Socially aware motion planning with deep reinforcement learning”. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2017, p.1343-1350.
- 6)
- Everett, M.; Chen, Y. F.; How, J. P. “Motion planning among dynamic, decision-making agents with deep reinforcement learning”. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2018, p.3052-3059.
- 7)
- Trautman, P.; Krause, A. “Unfreezing the robot: Navigation in dense, interacting crowds”. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2010. p.797-803.
- 8)
- Trautman, P.; Ma, J.; Murray, R. M.; Krause, A. Robot navigation in dense human crowds: Statistical models and experimental studies of human-robot cooperation. International Journal of Robotics Research. 2015, Vol.34, No.3, p.335-356.
- 9)
- Matsumaru, T.; Kusada, T.; Iwase, K. “Mobile robot with preliminary-announcement function of forthcoming motion using light-ray”. IEEE/RSJ International Conference on Intelligent Robots and Systems, 2006, p.1516-1523.
- 10)
- Kayukawa, S.; Higuchi, K.; Guerreiro, J.; Morishima, S.; Sato, Y.; Kitani, K.; Asakawa, C. “Bbeep: A sonic collision avoidance system for blind travellers and nearby pedestrians”. CHI Conference on Human Factors in Computing Systems, 2019, p.1-12.
- 11)
- Hardin, G. The tragedy of the commons. Science. 1968, Vol.162, No.3859, p.1243-1248.
- 12)
- Chen, C.; Liu, Y.; Kreiss, S.; Alahi, A. “Crowd-robot interaction: Crowd-aware robot navigation with attention-based deep reinforcement learning”. IEEE International Conference on Robotics and Automation. 2019, p.6015-6022.
- 13)
- Leibo, J. Z.; Zambaldi, V.; Lanctot, M.; Marecki, J.; Graepel, T. “Multi-agent reinforcement learning in sequential social dilemmas”. International Conference on Autonomous Agents and Multi-Agent Systems. 2017, p.464-473.
- 14)
- Robicquet, A.; Sadeghian, A.; Alahi, A.; Savarese, S. “Learning social etiquette: Human trajectory understanding in crowded scenes”. European Conference on Computer Vision. 2016, p.549-565
- 15)
- Chen, Y. F.; Everett, M.; Liu, M.; How, J. P. “Socially aware motion planning with deep reinforcement learning”. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2017, p.1343-1350.
- 16)
- Tai, L.; Zhang, J.; Liu, M.; Burgard, W. “Socially compliant navigation through raw depth inputs with generative adversarial imitation learning”. IEEE International Conference on Robotics and Automation. 2018, p.1111-1117.
本文に掲載の商品の名称は、各社が商標としている場合があります。














