3D TOFセンサモジュールへの誤差補正及び3次元座標変換の組込み
- 距離センサ
- TOF (Time of Flight)
- 3次元
- 高精度
- 距離画像
近年、工場で使用される自律走行ロボット、介護ロボットなど様々なサービスロボットにおいて、広い視野角で3次元(3D)の情報を取得できる3D TOFセンサに注目が集まっている。3D TOFセンサは空間の情報を取得できることから、これまで使用されてきた変位センサや2次元カメラからの代替が期待されている。TOF方式とは光の飛行時間から距離を計測する方式であり、TOFセンサは一般的なCMOSイメージセンサと同様に撮像した情報を電圧出力として読み出し、この出力データから距離を計算する。計算後の距離はセンサ毎に様々な要因の誤差を含むので、高い精度を得る為にはセンサ毎に適切な補正処理を行う必要がある。また、センサから直接得られるのは一次元の距離情報のみである為、距離情報と角度情報を合わせた3次元座標への変換処理も必要となる。これらの距離計算、補正や変換といった後処理をユーザ側のシステムで作り込むことは、ユーザ側の開発に大きな負担を生じさせる。
我々は、これらの処理をセンサ内で実現する為に、処理に必要な演算式は各センサ共通に組込み、演算に必要なパラメータは出荷時に個体毎に最適なものを書き込む仕組みを搭載した3D TOFセンサモジュールを開発し、1コマンドで3次元情報が高精度に取得できる機能を実現した。
1.まえがき
近年少子高齢化の進行による労働力人口の不足から、工場で使用される自律走行ロボット、介護ロボットといった様々なサービスロボットが広がりを見せており、広い視野角で3次元の情報を取得できる3D TOFセンサに注目が集まっている。3D TOFセンサは空間の情報を取得できることからこれまで使用されてきた変位センサや2次元カメラからの代替が期待されている1)。
TOFとはTime of Flight(飛行時間)の略で、光源から放射された光が対象物に反射して返ってくるまでの時間をもとに距離を計測する方式である。TOFセンサは、一般的なCMOSイメージセンサと同様に撮像した情報を電圧出力として読み出し、この出力データから距離を計算する。この距離データを用いて3次元情報に変換することになる。一般的にはこれらの演算を行うためのソフトウェア開発キット(SDK)が提供されているが、検出距離の高精度化を実現するには画素毎の誤差・レンズ組立の誤差・温度による誤差を個体毎に補正する必要があり、これらはユーザで開発していくことになり負担を生じている。
我々はこの負担を省くために、距離計算、補正や変換に必要な数式はセンサ内部に組込み、これらの処理に必要なパラメータは個体毎に最適なものを使用できる仕組みとすることでセンサ内での処理を可能とし、高精度を実現できる技術を開発した。
2.TOFの検出原理
2.1 TOFとは
TOFでは、光源から発せられた光が検出器に到達する時間を計測することで距離を算出する。
距離



この飛行時間を計測する手法は、直接法と間接法の2つに大きく分類される。
直接法では、光源から発せられた光が対象物にあたり、その反射光が検出器に到達するまでの時間を計測することで、光の飛行時間から距離を算出する。
間接法では、光を周期的に点滅させた発射光と対象物に反射して戻ってくる反射光の位相差から距離を算出する2)。
2.2 位相差方式
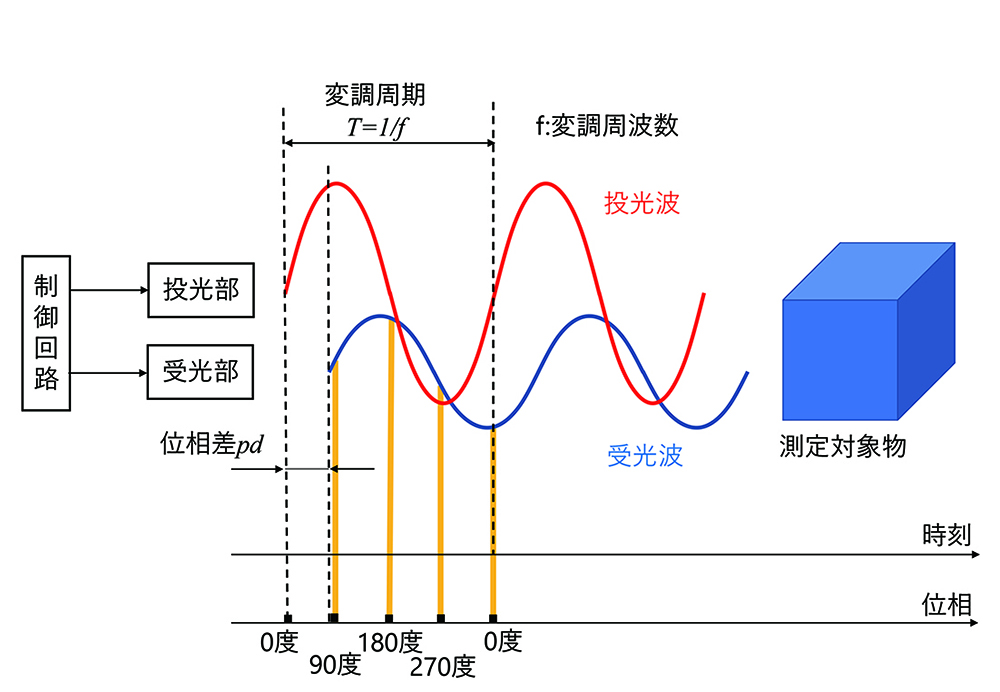
本TOFセンサでは間接法(位相差方式)を採用している。図1は位相差方式の原理を示している。投光部から放射された赤外光(投光波)は対象物に当たって反射し、戻ってきた赤外光(受光波)は受光部で検出される。対象物までの距離は投光波と受光波の位相差









-
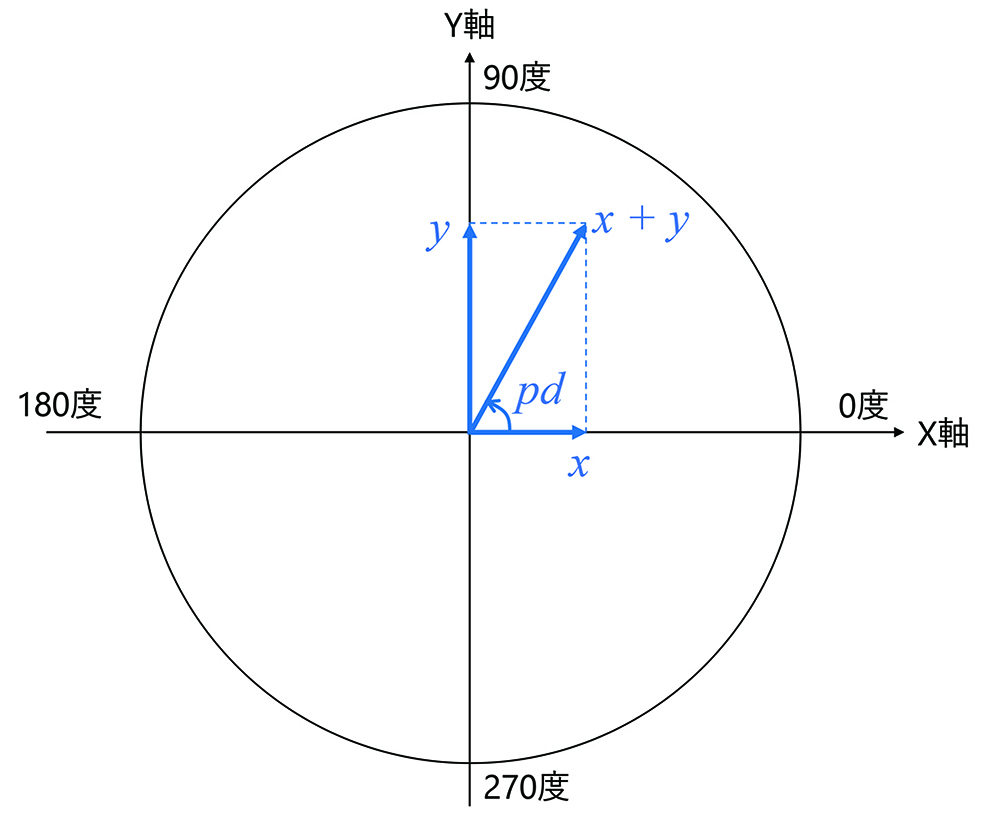
: 0度の受光量と180度の受光量の差分ベクトル
-
: 90度の受光量と270度の受光量の差分ベクトル
 の関係
の関係受光は、光により受光部内の素子で発生した電荷を蓄積することで得られる。図3に電荷蓄積の仕組みを模式的に説明する。
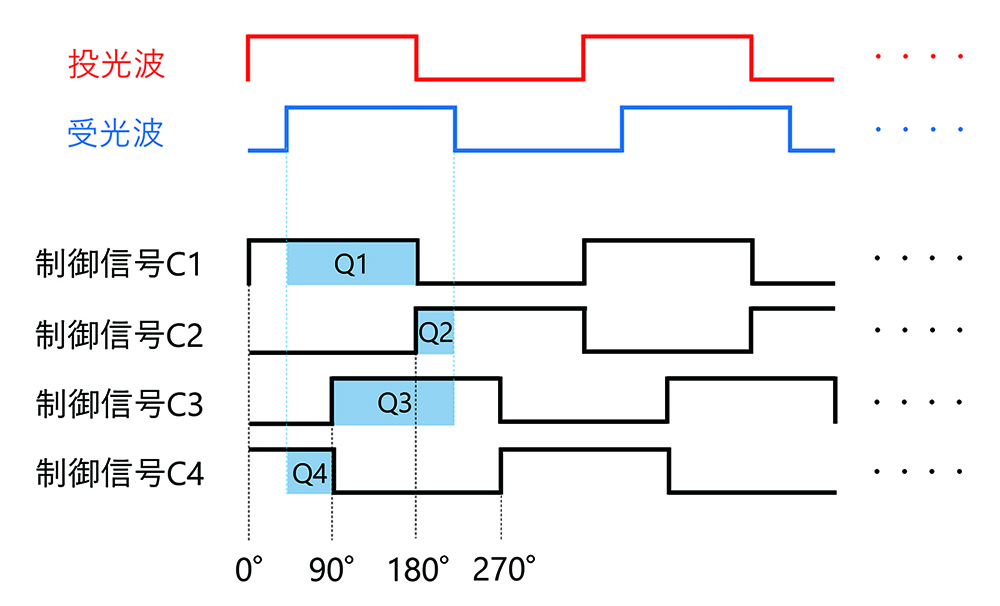
制御信号C1は投光波に対し位相遅延なしで生成される。電荷量Q1は、C1の立ち上がりから立ち下がりまでの期間において受光した光に相当する。同様に、電荷量Q2、Q3、Q4は、それぞれC2、C3、C4の立ち上がりから立ち下がりまでの期間において受光した光に相当する。
C1とC3、C3とC2、C2とC4の間には互いに90度の位相遅延の関係がある。したがって、受光は蓄積された電荷量に対応すること、位相差


測定できる最大距離は投光波1波長の半分となり






受光により得られた電荷量の大きさは、合成ベクトル


この
3.技術的課題
TOFセンサの用途として想定される自律走行ロボットでは、距離精度が低いと対象物との距離が正確でなく、衝突に繋がる恐れがある。また、人や物の判別、状態を検知するようなアプリケーションでは誤検出されることが想定される。このような事象を防ぐためには高い距離精度が求められる。
2章の検出原理より、距離は式(2)(3)から算出されることから、電荷量が正確であることが必要である。
電荷量は受光部のイメージセンサや集光するレンズ、投光部の発光回路に依存している。これらは、それぞれにロット、個体毎に固有のばらつき・誤差要因を有しており、ハードウェア的に完全に抑え込むことが難しく、個体毎に補正処理を行う必要がある。
しかし個体毎の補正処理をユーザが実施することは誤差要因の特定と対策が必要であるため負担となる。補正処理に関するユーザへの負担を軽減しつつ補正効果を最大化する為には、必要となる各種補正を個体毎に行う仕組みをセンサに組込む必要がある。また、蓄積される電荷量は対象物の距離や反射率にも依存するので、測定可能な距離を広げることや様々な対象物を測定する上での課題もある。
以下、補正処理が必要となる各種誤差についての課題を述べる。
3.1 距離の直線性に対する課題
式(2)を用いて求めた位相差





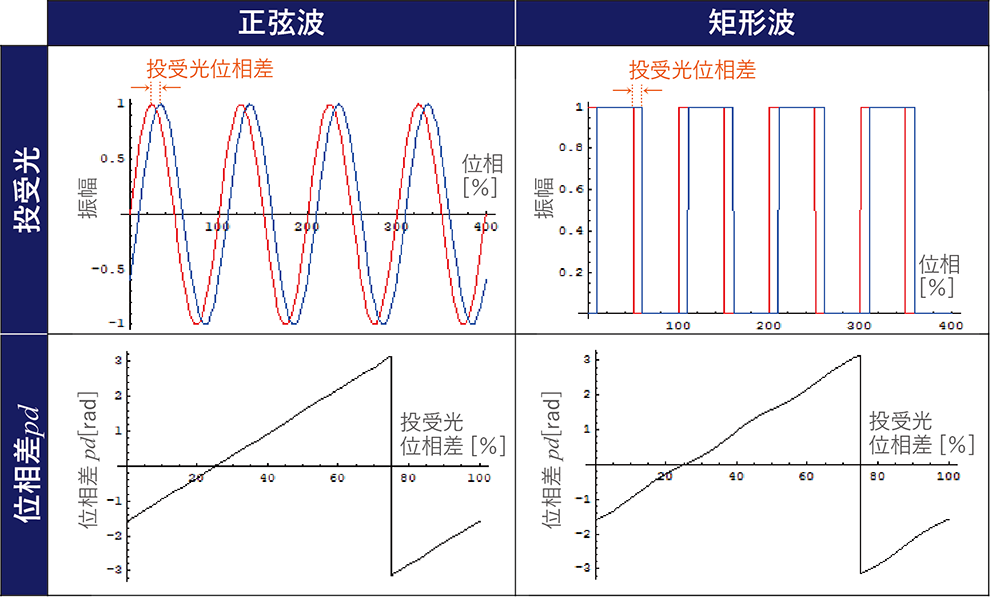
 の計算結果
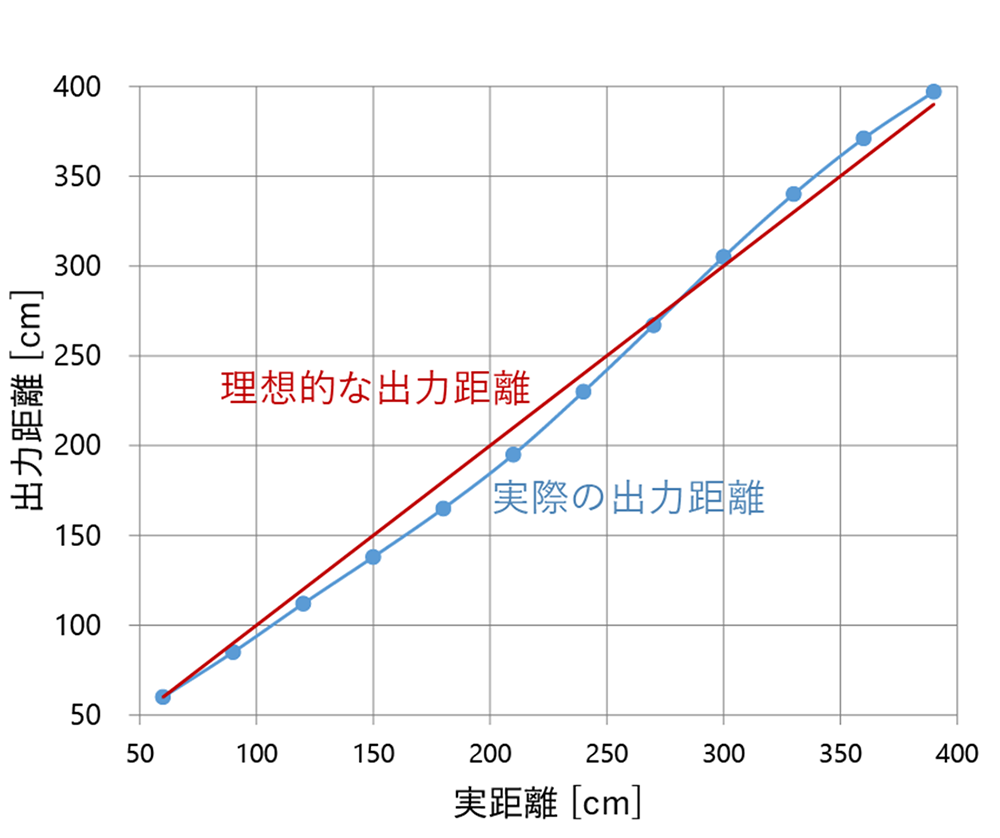
の計算結果図5は、実距離に対する出力距離を示したグラフである。横軸が実距離、縦軸が出力距離であり、矩形波投光を行った際の出力距離を青色でプロットしている。グラフから、実際の出力距離は赤の直線で示す理想的な出力距離に対して歪んでいることがわかる。これは、計測する対象物の位置によって距離値が実際よりも近く出力されてしまうことや、遠く出力されてしまうことを意味しており、安定した距離計測を行う為には距離の直線性を得ることが課題となる。
3.2 距離の画素間ばらつきに対する課題
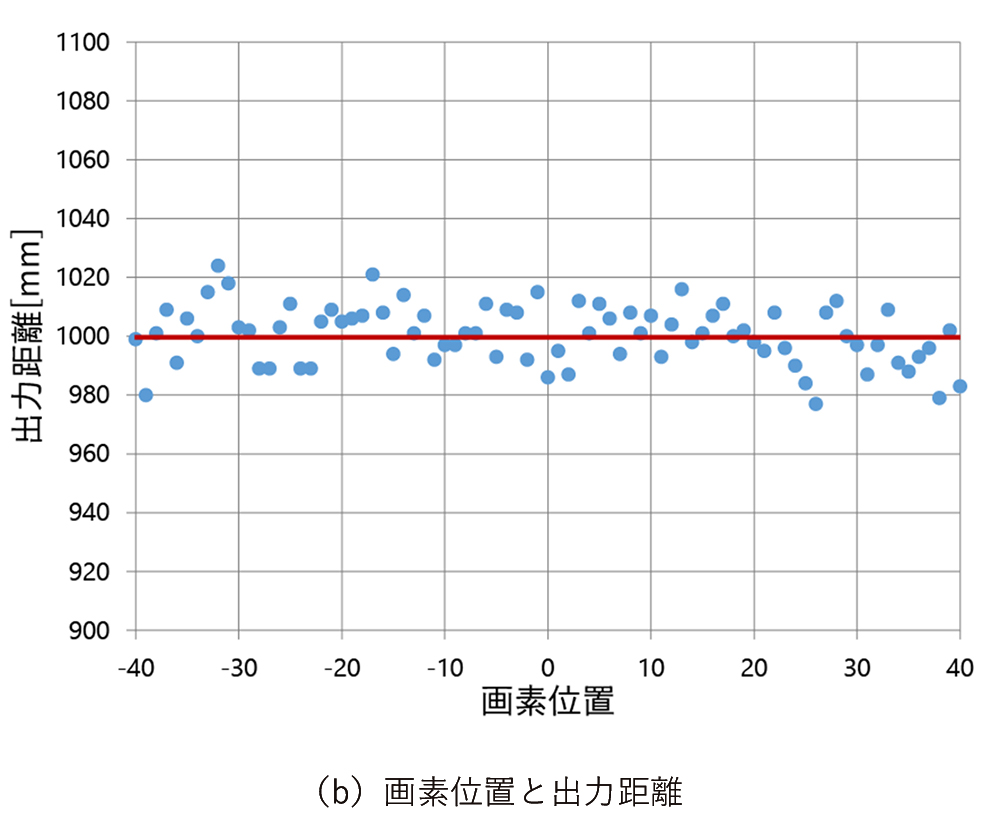
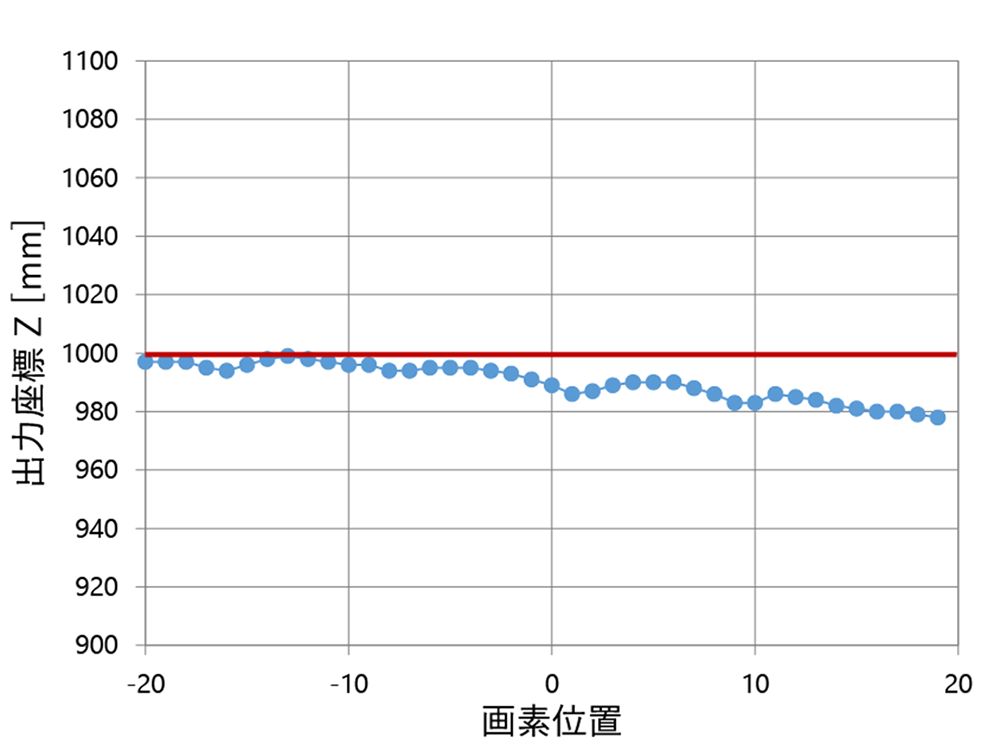
画素毎の直線性が得られたとしても、画素間における距離の出力にはばらつきがあり、平面上の同じ距離に対しても均一な距離が出力されない。図6は平面を測定した際の出力距離のばらつきを示したものである。図6(a)は測定環境を示しており、TOFセンサから1m離して測定対象平面を設置している。図6(b)の青色のプロット点は、図6(a)の測定対象平面の青線で示す中央の1ラインに相当するイメージセンサ上の各画素位置にて画素が出力する距離値を示している。線上の中心から±40画素分の各画素の位置を横軸、各画素の出力距離を縦軸にとる。一様な平面を測定した場合、理想的には赤線に示すような距離出力が得られるが、実際には赤線に対してばらついた距離値となっていることがわかる。
ばらつきは主に次のような要因で生じる。
- 画素の光電変換の感度
- 画素の電荷をAD変換する誤差

3.3 温度変化による距離変動に対する課題
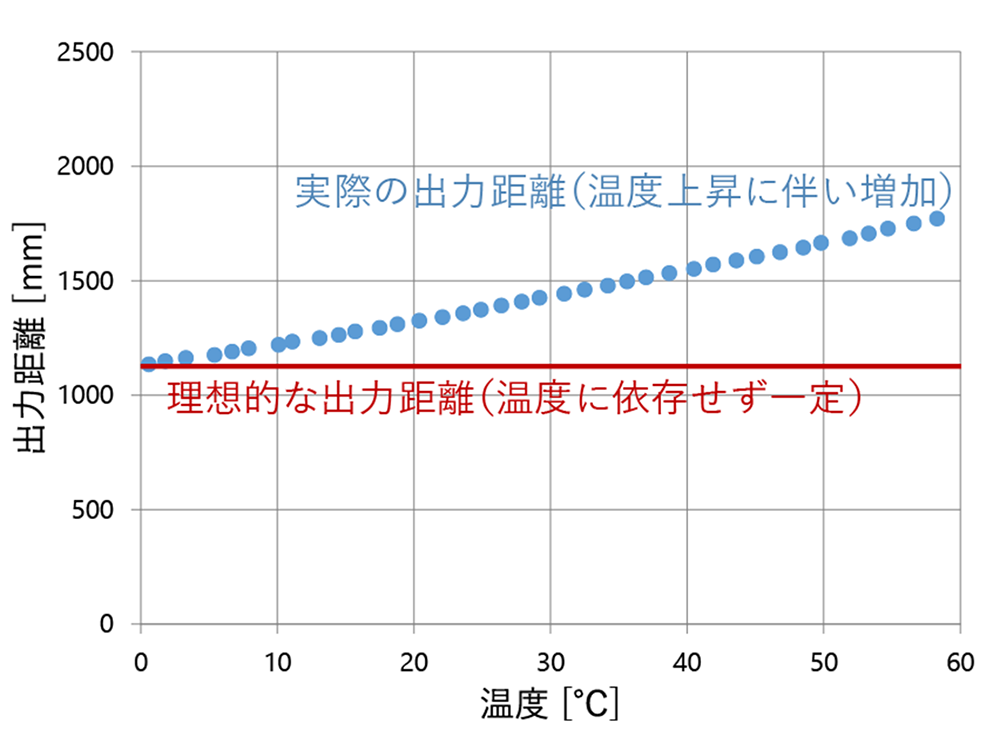
図7は対象物の位置が一定のもとで、温度を変化させた場合の出力距離を示したグラフである。横軸が温度、縦軸が出力距離であり、各温度における出力距離を青色でプロットしている。図7中に赤の直線で示すように温度変化に依存せず一定の距離値を出力することが理想であるが、実際には温度上昇に伴って“遠い”距離を出力するようになっていることがわかる。このような温度変化に伴う距離の変動を抑制し、温度変化に対して安定な距離計測を行うことが課題となる。
温度変化による距離の変動は主に次のような要因で生じる。
- 制御回路から投光させるタイミングの遅延
- 制御回路から受光させるタイミングの遅延
- 画素の光電変換の感度
3.4 測距レンジ及び対象物反射率に対する課題
2.2節で述べたように測定できる最大距離値は投光波の周波数により決まるが、測定するには十分な電荷量を蓄積する必要がある。そのため、実際に測定できる距離はイメージセンサで電荷を蓄積する時間によって決まり、蓄積される電荷量は受光する光量に依存する。式(4)で示したように電荷量は受光強度(振幅値)


一方、近い対象物や反射率の高い対象物を測定する為には電荷を蓄積する時間を短くする必要がある。これは、イメージセンサの画素が蓄積できる電荷量に上限がある為で、電荷を蓄積する時間が長いと電荷量が飽和して、距離が正しく計算できなくなる。
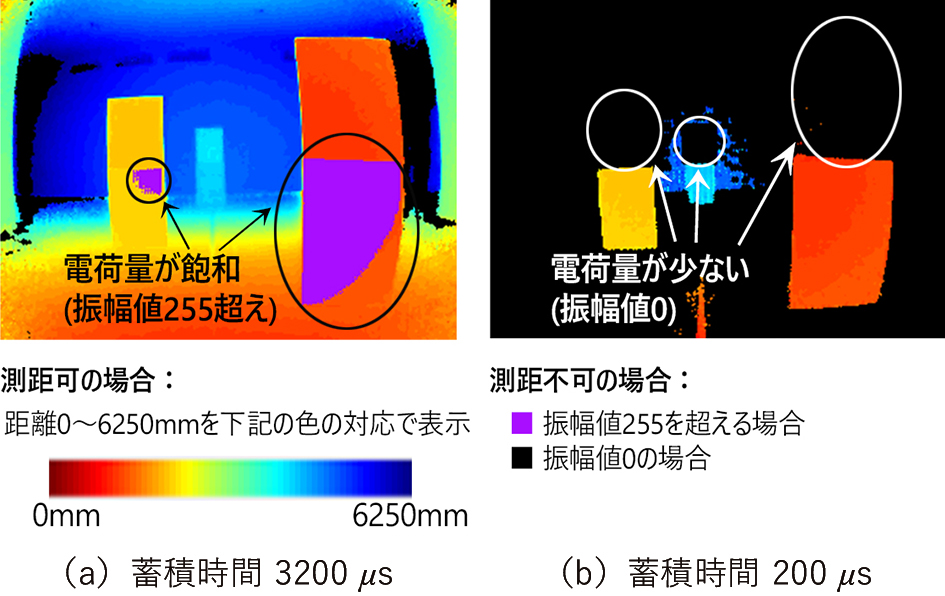
図8に蓄積時間による測距レンジの違いを測定した環境を示す。TOFセンサからの距離1m、2m、4mの各位置に反射率56.3%の白紙と反射率5.5%の黒紙を張り付けたボードを設置し測定している。図9に蓄積時間による測距レンジの違いを示す。図9(a)に蓄積時間3200



つまり、測定したい対象物までの距離や反射率に応じて蓄積時間を設定する必要があり、このことは距離の近い対象物と距離の遠い対象物、反射率の低い対象物と反射率の高い対象物を同時に測定できないことを意味し、測距レンジ・対象物反射率レンジを広げることが課題となる。

3.5 3次元変換に対する課題
3D TOFセンサは一般的なCMOSイメージセンサのように撮像範囲内の距離情報を取得できるが、これは各画素から対象物までの1次元の距離情報を取得しているのみである。対象物の大きさや形、または対象物間の距離を測る用途においては、3次元座標情報の取得が必要となる。
1次元の距離情報を3次元座標情報に変換する為には、イメージセンサから得られる各画素の距離情報に加えて、各画素がレンズを通して見通す角度の情報が必要になる。図10に1次元の距離と3次元座標の対応を示す。図10の














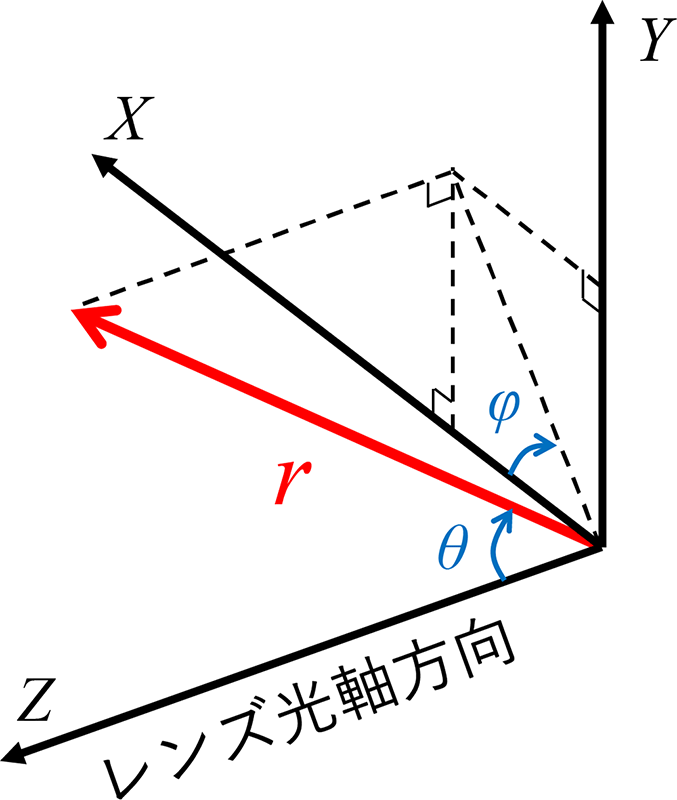
- X : 3次元空間上のX座標
- Y : 3次元空間上のY座標
- Z : 3次元空間上のZ座標
- r : 各画素から対象物までの距離
-
: rとZ軸がなす角度
-
: XY平面上の回転角度
4. 補正方法及びその効果
3章で述べた通り、距離出力結果は各要因による誤差が含まれ、これらの誤差は個体毎に固有な物であることから、個体に合わせた補正を行う仕組みが必要である。従来はこれらの補正を共通のPCソフトで行っており個体毎に最適な補正とはなっていなかった。
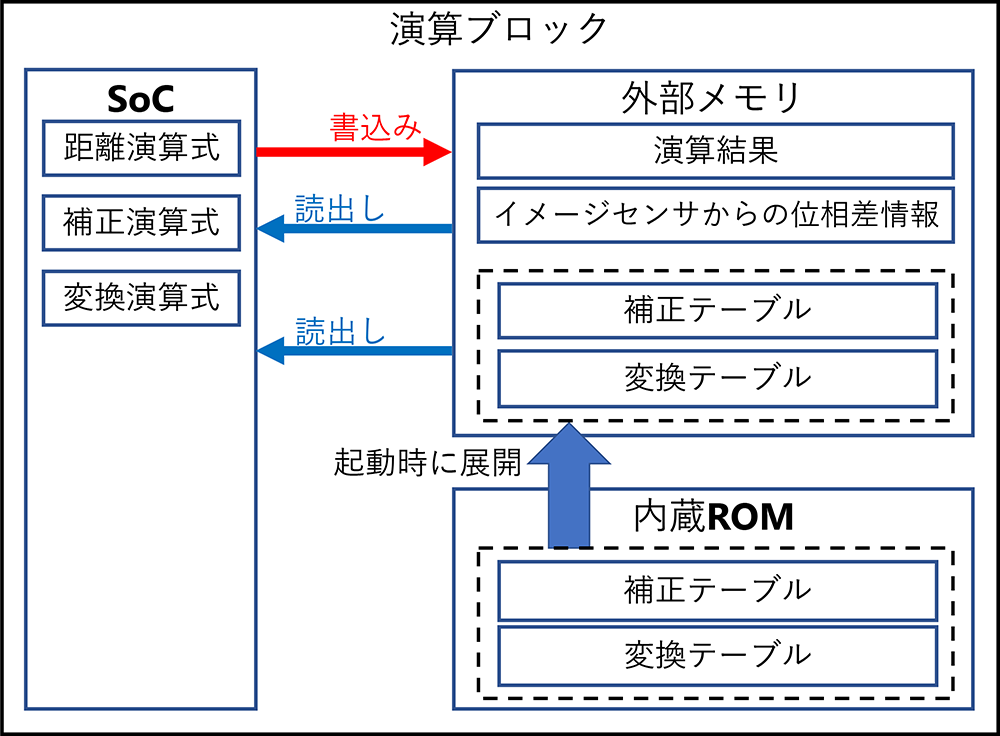
我々のTOFセンサに搭載されている演算ブロックは、図12に示す通り、SoC、外部メモリ、内蔵ROMから構成されている。補正や変換などの演算式はSoC内部に組み込まれている。演算に必要な個体毎の固有パラメータ情報については、出荷時に最適なものをテーブル化して内蔵ROMに書き込んでいる。ユーザがTOFセンサを起動すると、テーブルデータを内蔵ROMから外部メモリに読出し、イメージセンサから取得した位相データを用いてSoCにて距離演算及び補正、座標変換の演算を行う。
以降、3章で述べた距離精度を得る為の個別の課題に対する解決策及びその効果について述べる。
4.1 距離の直線性の補正
補正前の距離値は3.1節の図5に示すように、理想的な直線に対する歪みを有している。
理想的な直線に近づける為に、投光波が矩形波から正弦波になるような駆動回路を実装した。しかしながら、現実には理想的な正弦波を得ることは困難であり、得られた距離値に対する補正も必要となる。
補正を行う為に必要となる、歪み量を計算する為のパラメータは個体毎に求めておき、出荷時にテーブル化してセンサ内部に格納する。歪み量の計算には、各センサ共通に独自の式を設定し組み込んでいる。センサ使用時には、個体毎に固有のテーブルを用いて歪み量を求める為、各センサで最適な補正済み距離を出力することが可能となる。
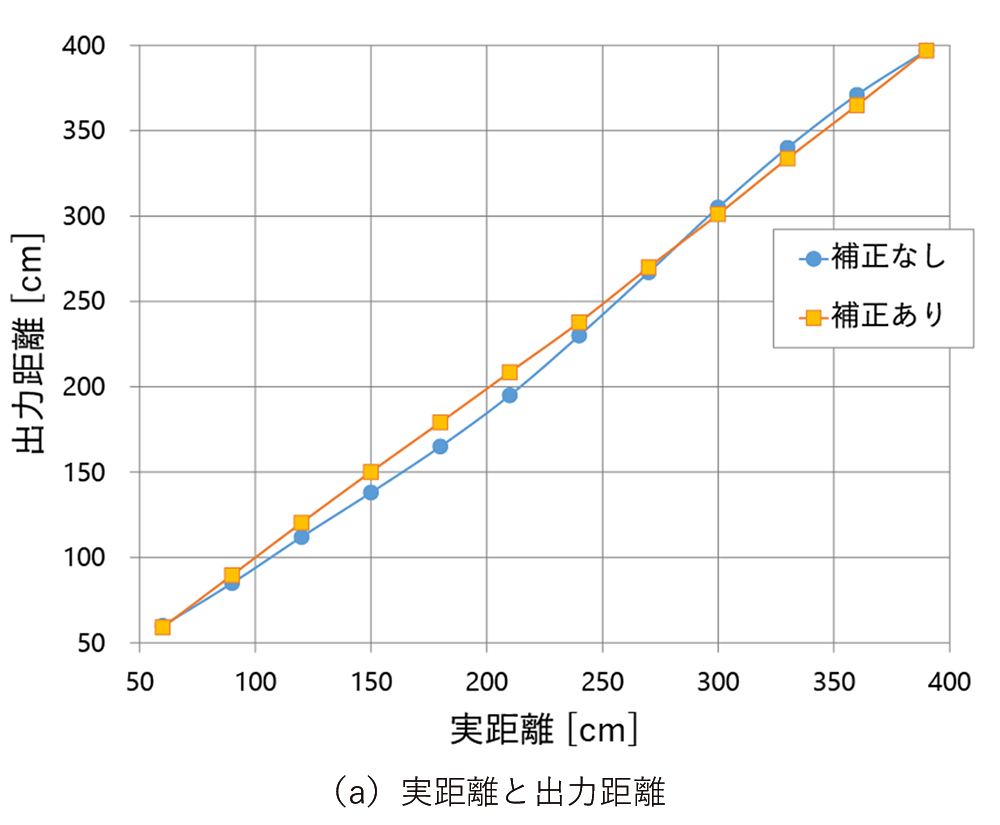
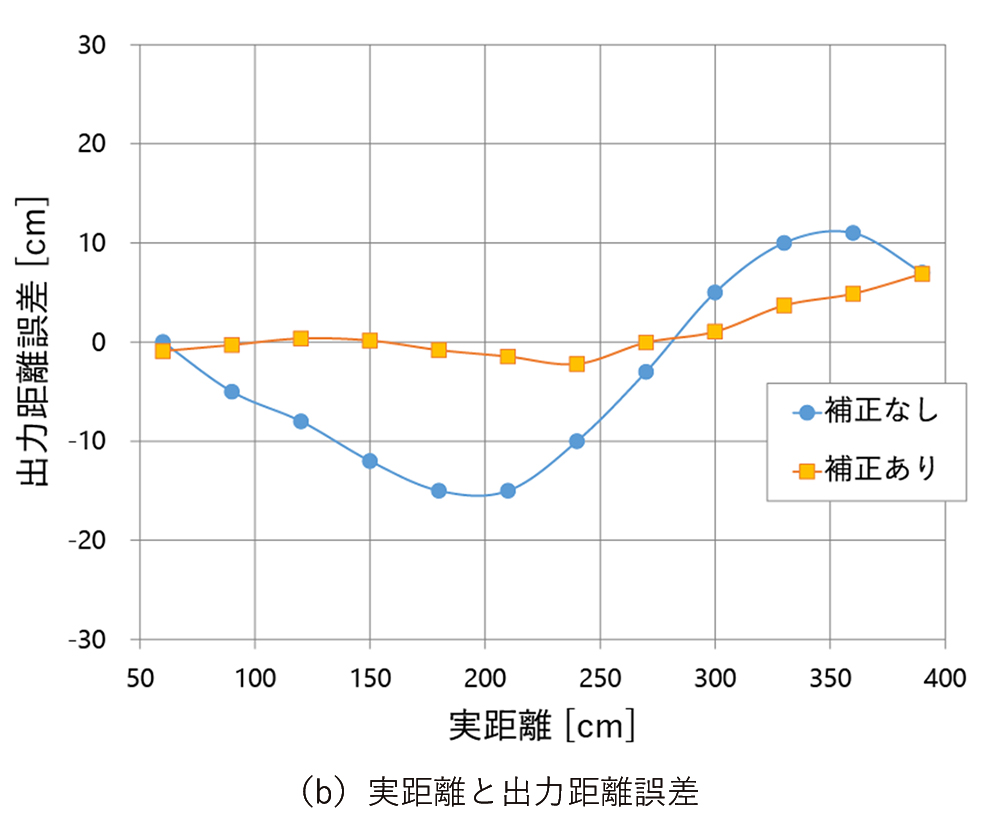
図13(a)は、実距離と出力距離の関係を示したグラフであり、横軸にイメージセンサから対象物までの実際の距離値、縦軸にイメージセンサが出力する距離値を示している。図5で示したグラフと同様の補正無しのものを青色でプロットし、本補正を実施して得られた補正ありのものを橙色でプロットしている。図13(b)は、図13(a)における出力距離の真値からの誤差を縦軸として取りなおして示している。図13(a)(b)の補正ありのものと補正なしのものを比較すると、補正ありのものは補正なしのものと比較して距離の直線性が向上しており、距離の誤差も減少している。
4.2 距離の画素間ばらつきの補正
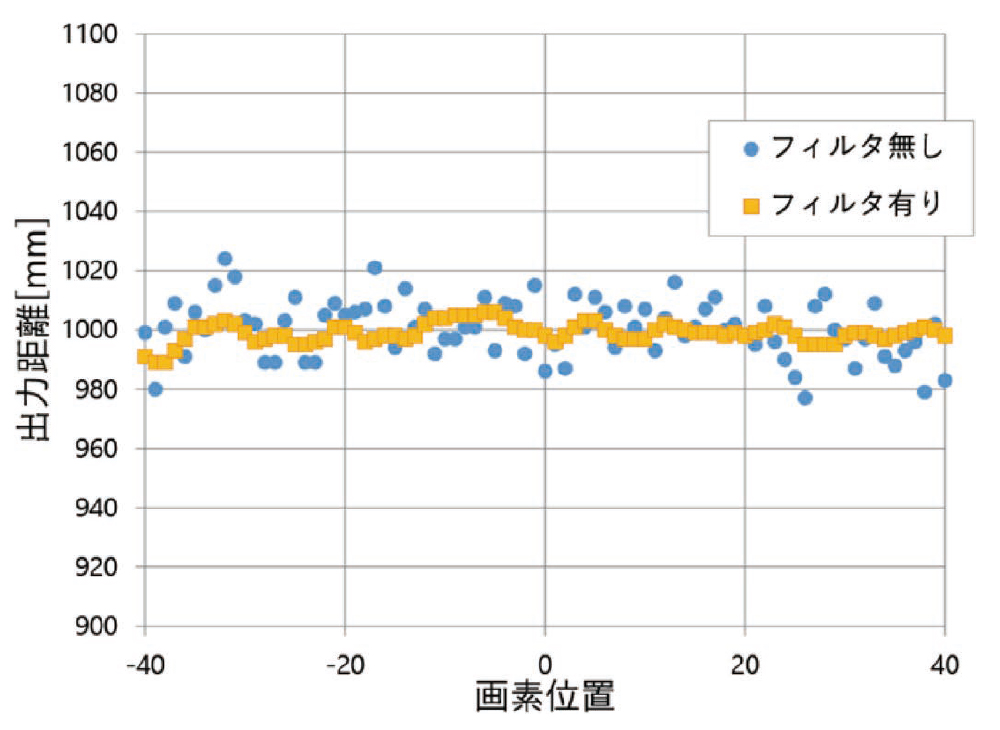
画素毎の距離の直線性が得られた上で、画素間のばらつきを抑える為に空間フィルタを用いた画素間の距離値の平滑化を合わせて行う。図14にフィルタ有りとフィルタ無しによる画素間の出力距離のばらつき比較を示す。測定環境は図6(a)と同様に平面を測定し、青線で示す中央の1ラインに着目する。図14のグラフは、このライン上の中心から±40画素分の各画素の位置を横軸にとり、各画素の出力距離を縦軸にとったものである。青色で示すプロット点がフィルタ無しの場合であり、橙色で示すプロット点がフィルタ有りの場合である。このグラフより、フィルタリングを実施した後ではフィルタリングを実施する前に比べて、画素間のばらつきが軽減されている。
4.3 温度変化による距離変動の補正
3.3節で述べた通り、温度変化に伴う投光/受光タイミングの遅延は距離値の変動を生じさせる。我々のTOFセンサでは、投光部の温度を取得する温度センサと受光部(イメージセンサ)の温度を取得する温度センサをそれぞれ搭載している。
温度による距離値の変動量は、投光部、受光部それぞれの回路のばらつきに依存して変化する。
補正を行う為に必要となる、投光部の温度に依存する距離変動量を計算する為のパラメータと受光部の温度に依存する距離変動量を計算する為のパラメータは個体毎に求めておき、出荷時にセンサ内部に格納する。距離変動量の計算には、各センサ共通に独自の式を設定し組み込んでいる。センサ使用時には、個体毎に固有のパラメータと、使用時の投光部及び受光部の温度を用いて距離変動量を求める為、各センサで最適な補正済み距離を出力することが可能となる。
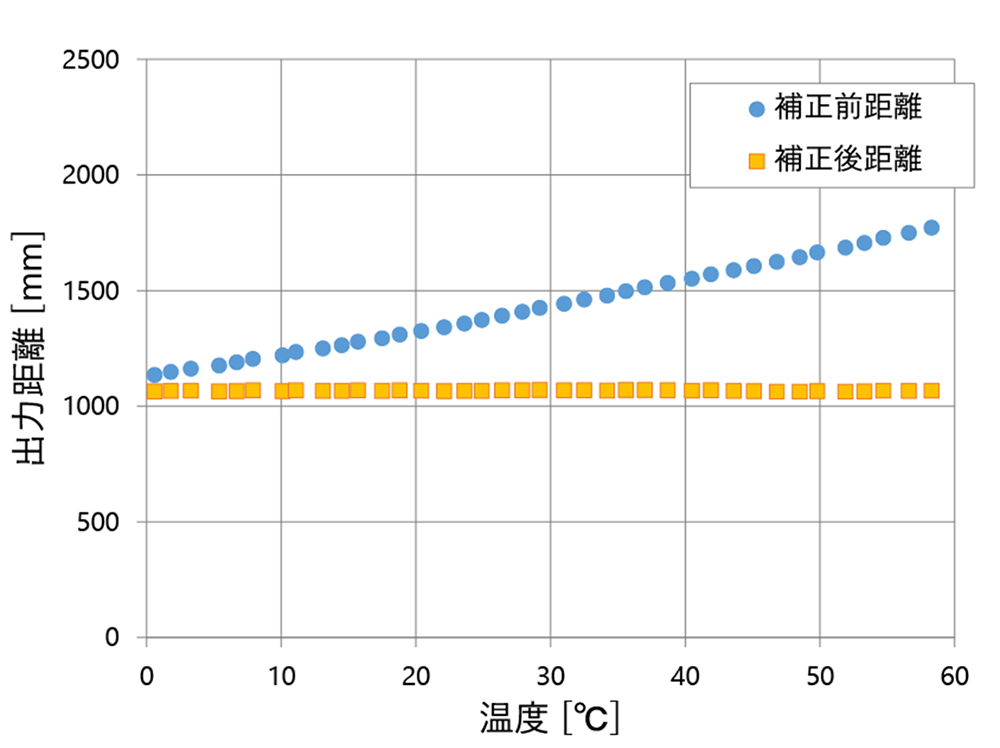
図15は、温度と出力距離の関係を示したグラフであり、横軸にイメージセンサの温度、縦軸に出力距離を示している。図7で示したグラフと同様に補正前距離を青色でプロットし、この値に対して本補正による補正計算を実施した結果を補正後距離として橙色でプロットしている。補正前距離と補正後距離を比較すると、補正後距離は補正前距離に対して温度に対して安定な距離値が得られている。
4.4 距離・反射率レンジを広げるHDR処理
3.4節で述べた通り、近い対象物と遠い対象物、反射率の低い対象物と高い対象物は同時に測定できない為、近い対象物や反射率の高い対象物用に蓄光時間を短くして撮像した距離画像と遠い対象物や反射率の低い対象物用に蓄光時間を長くして撮像した距離画像を合成する。
測距可能な距離や反射率のレンジを広げるHDR(High Dynamic Range)の処理の概要は、2枚の画像を画素毎に比較し、いずれかが飽和している場合は飽和していない方を採用し、両者とも飽和していない場合は受光量の大きな方を採用するというものである。
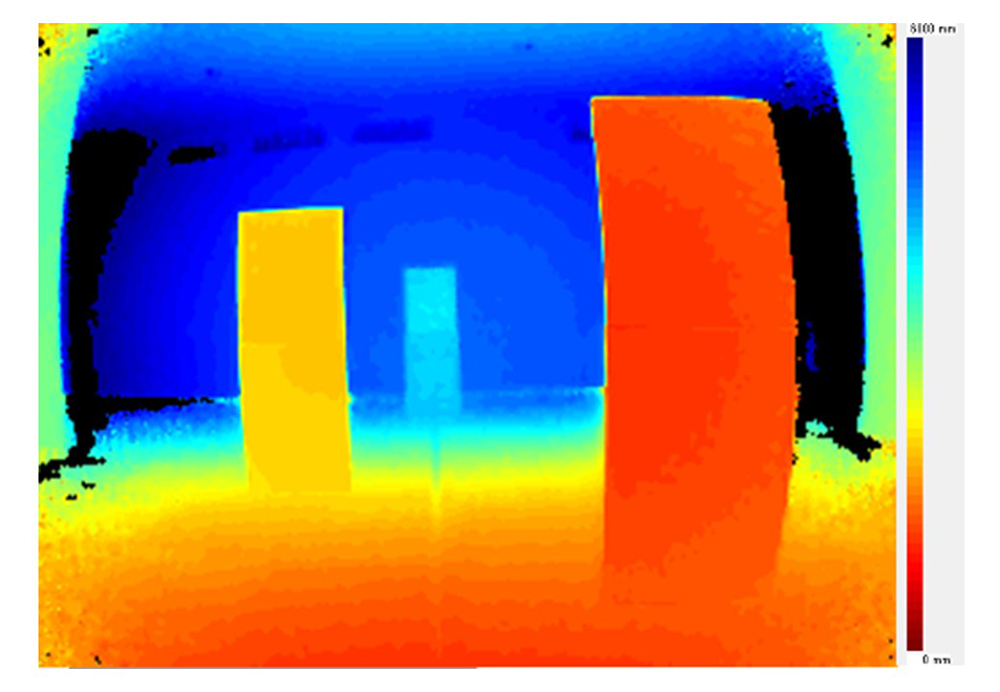
図16にHDRによる効果を示す。3.4節の図9においては、遠い対象物と近い対象物、反射率の高い対象物と低い対象物を同時に測定することができなかったが、近い対象物、遠い対象物、反射率の高い対象物、反射率の低い対象物が全て測定できており、幅広い距離・反射率のダイナミックレンジが得られている。
実環境においては、任意の位置に様々な反射率の対象物が存在する状況が想定される為、本HDR処理の実現で、TOFセンサ使用上の環境的な制約条件の緩和に繋がる。
4.5 3次元変換
3.5節で述べた通り、1次元の距離情報を3次元座標に変換する際には、角度誤差の影響を考慮する必要がある。図10で示した3次元座標












図17にレンズの軸ずれを考慮した軸ずれ無しの






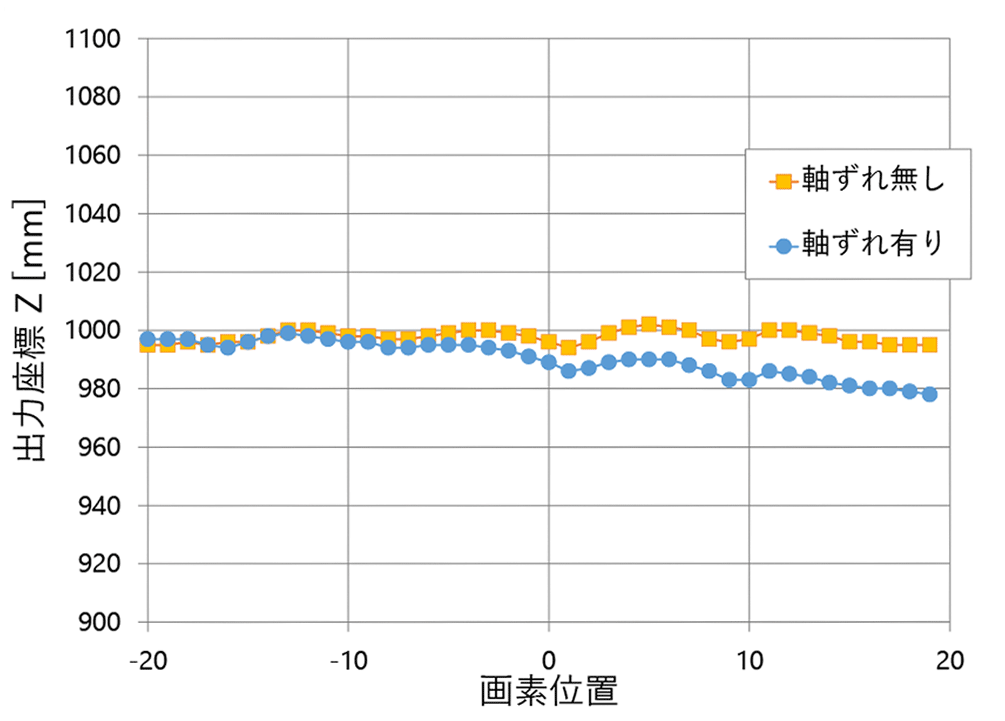
4.6 補正効果のまとめ
4.1節、4.2節、4.3節、4.5節で述べた各種補正について、補正前後の距離誤差の比較結果を表1に示す。距離誤差の値は、真値に対する誤差の比率を百分率で表現しており、いずれの補正においても距離誤差2%以下の高精度な距離出力を実現できていることがわかる。
| 補正各種 | 距離誤差 (補正前)[%] |
距離誤差 (補正後)[%] |
|---|---|---|
| 距離直線性補正 | 8.3 | 1.8 |
| 画素間ばらつき補正 | 2.4 (標準偏差:0.98) |
0.6 (標準偏差:0.33) |
| 温度補正 (0~60℃) |
67.8 | 0.11 |
| 3次元変換 | 2.2 | 0.6 |
また、4.4節で述べたHDRについて、表2に示すHDR有り・無しそれぞれにおける距離・反射率の比較結果から、距離1m~4m、反射率5.5%~56.3%の広範囲にわたって測距可能となったことがわかる。
| 測距対象 | HDR無し | HDR有り | ||
|---|---|---|---|---|
| 距離[m] | 反射率[%] | 蓄積時間 3200μs |
蓄積時間 200μs |
|
| 1.0 | 5.5 | ○ | × | ○ |
| 56.3 | × | ○ | ○ | |
| 2.0 | 5.5 | ○ | × | ○ |
| 56.3 | × | ○ | ○ | |
| 4.0 | 5.5 | ○ | × | ○ |
| 56.3 | ○ | ○ | ○ | |
5. むすび
3D TOFセンサモジュールには個体毎に固有のばらつき・誤差要因があり、高精度を求めるアプリケーションではユーザ側のシステムで補正処理を行う必要があった。
本開発はこれらの課題を解決する、個体毎に最適なパラメータを書き込める仕組みと演算処理を搭載することで、1コマンドで3次元情報が高精度に取得できる機能を実現した。
3次元センサは、労働力人口の不足やコロナ禍での3密回避による省人化ニーズの高まりにより、工場や物流倉庫内の搬送などの産業用途のみならず、公共施設や病院、駅、商業施設での高度な作業領域での活躍も期待されている1)。今回の開発はそのような社会ニーズに対して一つのソリューションを与えるものとなった。
今後は更なる顧客ニーズにこたえるため、検出できる距離、画角、反射率の範囲を広げる検討を進めていきたい。
参考文献
- 1)
- オムロン株式会社.“人や物との距離を3次元でリアルタイムに測定する組み込み型TOFセンサモジュール「B5Lシリーズ」を発売”.
https://www.omron.com/jp/ja/news/2020/09/c0901.html,(参照2020-09-01). - 2)
- 安富啓太,川人祥二.Time-of-Flightカメラ.映像情報メディア学会誌.2016, Vol.70, p.880-882.
- 3)
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R. Time of Flight Cameras:Principles, Methods, and Applications. Springer, 2012, p.8-10.
本文に掲載の商品の名称は、各社が商標としている場合があります。














